【原创】方差分析原理解析

潜水很长时间，第一次发帖请多关照。今天是元宵佳节，祝大家团团圆圆，元宵节快乐安康。
在论坛中潜水期间，学习到了很多专业人士的卓越见解，因此也希望所学所获能与大家分享，算是一种感恩与回馈。
文章来自微信公众号“Excel与Minitab”大家不要误会，并非广告贴，只因微信公众号的文章能插入动态图片便于阅读与在Minitab中操作。原文链接如下就不显示了。
我们比较两个正态样本时可以采用假设检验，如果我们要比较三个样本是否有差异时，例如我们要比较三个供应商提供的同一类型的零件强度是否有明显差异，在我们用双样本假设检验进行两两比较，甲乙，甲丙，乙丙，需要比较三次，且置信水平为0.95%3=85.7%，如果我们比较更多的样本时，比较的数量以及置信区间均无法满足我们的需求，这时假设检验已经无法适用，在此我们引入方差分析的方法比较多个均值是否一致。因此方差分析的前提条件与双样本假设检验的前提条件是一致的，即满足：1，每一个总体的分布需要符合正态分布 2，各正态总体的方差相等 3，确保数据的独立性。
现实中，我们理解的方差分析不仅仅用于多个等方差正态总体的均值之间的比较；当我们怀疑某个变量(X)对结果(Y)可能存在影响时，我们需要在不同的X下，例如对X分别取值X1,X2,X3(X的三种水平下重复试验)比较与之对应的Y1,Y2,Y3,然后我们使用方差分析比较Y1,Y2,Y3的均值，以确定X对于Y来讲是否为一个有影响的因素，试想如果X对Y没有影响，不论X取什么值，只要其他条件不变输出Y都应该是差不多的，用专业的统计术语即试验的观测值Y们之间的均值没有显著差异，因此方差分析是我们找寻关键因素的关键。
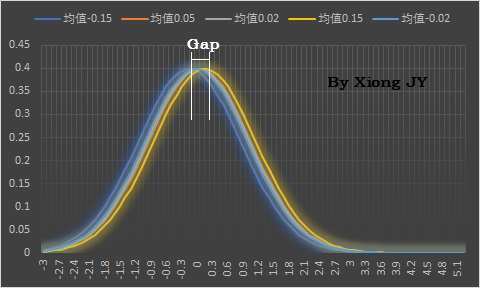
基于上述三个基本条件，我们在单因子ANOVA分析过程中其实就是比较多个等方差的正态分布他们的均值有无显著差异，如果H0成立，各水平下的均值无显著差异，如下图，分布均值的Gap很小；


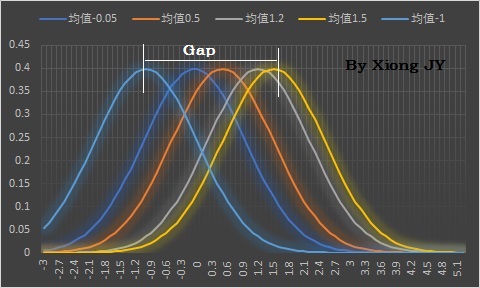
如果H1成立，即各水平下的均值不完全相同，如下图，分布均值的Gap很大。


其分析原理：

(组间方差/自由度A)：(组内方差/自由度e)服从F分布--我们在《三类等方差检验》一文中讲过F分布，两个独立的卡方分布（正态分布的平方和）除以各自自由度服从F分布，我们在此用于方差分析，如果F值落入拒绝域，认为Gap足够大，即该因子影响显著。注意其中组间偏差的自由度fA=水平数r-1，组内偏差自由度=试验总次数n-水平数r。
读到这里，也许你已经完全明白了，也许还不是太明白方差分析的原理，我们比较均值最终是通过比较方差来实现的，为什么？为什么方差分析法可以分析各样本均值是否相等？通过5WHY我们再理一理其中的逻辑，如下图：


通过一个例子我们再次理解一下上述5WHY图中所述的随机误差与系统误差。
判断温度是否对产出有影响，在4个不同温度下分别进行了5次试验


 
我们看到即使在同一温度下，例如60度下的五个产出值并不完全一样，因为过程受到一些随机因素的影响，这时实测值与理论真值（我们通常认为平均值接近于理论真值故实际计算时用均值代替，下文的均值等同于理论真值）的偏离（方差）为随机误差，同一温度下各测量值与该温度下均值的方差又称之为组内方差，所以组内的方差只包含随机误差；我们再来看不同温度下的产出值，它们的均值上的差异时由于温度不同造成的，我们称之为系统误差，从数据上来看，不同温度组的产出值的组间方差既有不同温度带来的系统误差，也有随机因素造成的随机误差。如果该因素“温度”并不影响产出的话，那么组间方差中的系统误差部分应该接近于0，那么总的组间方差应该会接近于总的组内方差（组内方差只含随机误差），二者的比值就接近于1；反之，如果该因素对于输出有显著影响的话，组间方差则主要由系统误差构成，总的组间方差与总的随机方差的比值就比较大，而且该值越大因子效应越显著。根据前文统计基础《三大分布》中所述，两组方差与自由度之比（两卡方分布之比）符合F分布，因此方差分析的统计量为F值=(组间方差/自由度A)：(组内方差/自由度e)，拒绝域临界值为F1-α(dfA,dfe)。
相关案例如何在Minitab中操作，由于无法显示动态gif图片，就在本文省略了。文章不足之处，欢迎大家批评指正，谢谢。圣人云：“君子以文会友，以友辅仁”，Email：[email]neverlookbackxjy@163.com[/email]