1分钟教你制作一元线性回归分析

您是某种产品的制造商，希望对产品的质量进行度量，但度量过程花费太高。可以采用一种间接方式，即采用另一产品分值（分值 1）来替代实际质量度量（分值 2）。这种方法费用相对较低，但精确度也较低。您可以使用回归来分析“分值 1”是否能够解释“分值 2”中的大部分方差，以确定“分值 1”是否能作为“分值 2”的替代。
数据如下:
 
分值 1    分值 2
4.1    2.1
2.2    1.5
2.7    1.7
6.0    2.5
8.5    3.0
4.1    2.1
9.0    3.2
8.0    2.8
7.5    2.5
 
操作:
1, 6SQ统计--回归分析--一元线性回归分析

 
2，输入Y数据范围 分值2 输入X数据范围 分值1

 
3, 点击确定，输出结果。


 


 


 


解释结果


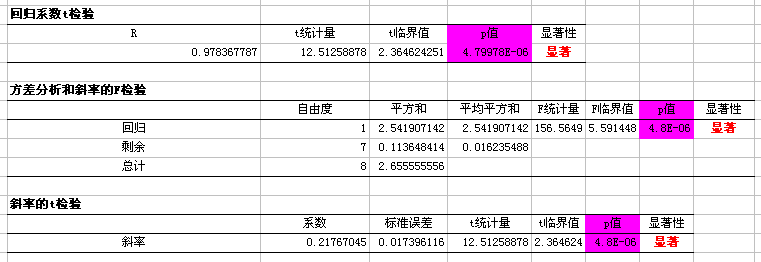
·    方差分析表 中的 p 值 (0.000) 表明在 a 水平 为 0.05 时“分值 1”与“分值 2”之间的关系具有统计上的显著 性。“分值 1”的估计系数 的 p 值 0.000 也证明了这一点。

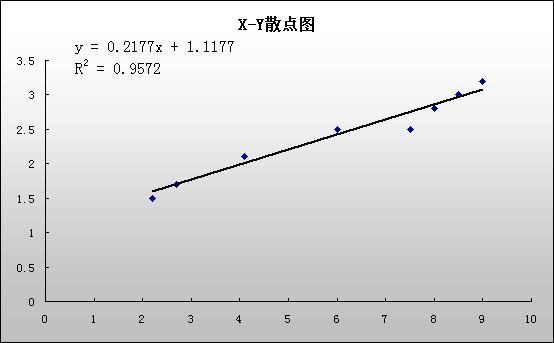
·    R2 值显示“分值 1”解释了“分值 2”中 95.7% 的方差，表明模型与数据拟合得非常好。

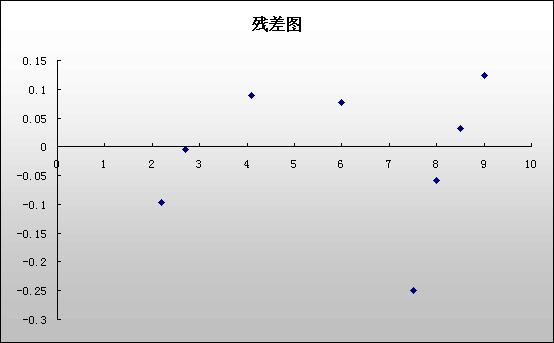
·    观测值 9 被标识为异常观测值 ，因为它的标准化残差 小于 -2。这就证明这个观测值是一个异常值。请参见识别异常值。

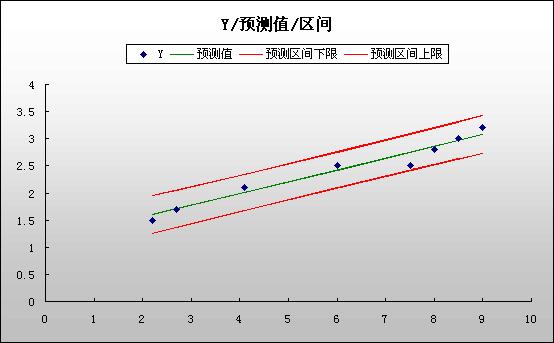
由于该模型是显著的，它解释了“分值 2”中的大部分方差，因此制造商决定使用“分值 1”替代“分值 2”作为产品质量的度量标准。
 
Excel案例数据:
 
6SQ统计3.0企业版90天试用下载​ http://pan.baidu.com/s/1i5AXSRN    

• 一元线性回归分析.xls