为什么化学工程师应该了解方差分析
一般来说,如果您是一名化学工程师,您可能正在开发和设计化工制造工艺。与其他工程师不同,化学工程师可能需要应用化学、生物学、物理学和数学原理来解决与化学品、燃料、药物、食品和许多其他产品的生产或使用相关的问题。因为将所有时间都用在了科学方面,如果您没有如所希望的在统计上花费足够时间,请不必担心,Minitab 随时为您服务!现在,让我们谈谈为什么方差分析 (ANOVA) 可以成为化学工程师的秘密武器。
为什么您应该了解方差分析
许多工业应用都需要进行实验,其目的是了解组之间是否存在差异。在统计方面,我们考虑一个因子(比如:催化剂类型)并且想了解该因子的各水平(比如:催化剂 1、2、 3 和 4)之间在统计意义上是否有显著差异。当各组的测量是连续的并且满足某些其他假设时,我们使用方差分析来比较各组的平均值。从某种意义上说,“方差分析”这个用词并不恰当,因为我们比较的是各组的均值。然而,通过分析组水平内和组间数据的变化,我们可以确定组均值是否在统计意义上不同。
方差分析检验总体均值(以符号 µ 表示)均相等的原假设。我们将使用样本均值来估计总体均值。如果这个原假设被否定,那么得出的结论是总体均值并不完全相等。
原假设:Ho: µCatalyst 1 = µCatalyst 2 = µCatalyst 3 = µCatalyst 4
简单地说,我们假设各组的均值相等,我们收集证据来证明这一点,即如果我们观察到这些均值之间存在较大差异,则更有可能否定此观点并假设组水平内存在差异。
单因子方差分析示例
想象一下,化学工程师想要比较使用四种不同催化剂的产品产量。 她将催化剂加热与产品一起反应。使用方差分析,工程师可以确定使用不同催化剂的产品产量是否有显著差异。
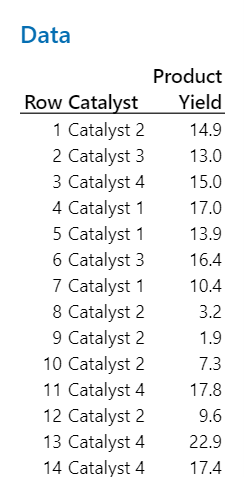
首先,工程师收集数据,如下所示。
接下来,运行单因子方差分析。
产品产量方差分析的 p 值很小,表明如果原假设成立,即催化剂均值相等,我们观察到这些结果的可能性很小。由于 p 值小于 5% 显著性水平(使用 alpha = 0.05),我们否定原假设。得出的结论是不同催化剂组的平均产品产量不同。
工程师即得知某些组的均值不同。下一个逻辑问题是哪些组的均值不同?
使用 TUKEY 法进行多重比较
虽然通过方差分析,我们知道了某些组的均值不同,但工程师需要进行更深入的比较才能了解到底哪些组的均值不同。Minitab 为此提供了“比较”功能。在我们的示例中,化学工程师使用 Tukey 比较来正式检验组对之间的差异,以了解哪些组对在统计上有显著差异。
Tukey 多重比较检验是多项检验中最保守的检验,可用于确定一组均值中的哪个均值与其他均值不同。方差分析之后使用 Tukey 法(这就是为什么您可能会听到被称为事后检验的方法),可用于为因子水平均值之间的所有成对差异创建置信区间,同时将整体误差率控制在指定的水平。
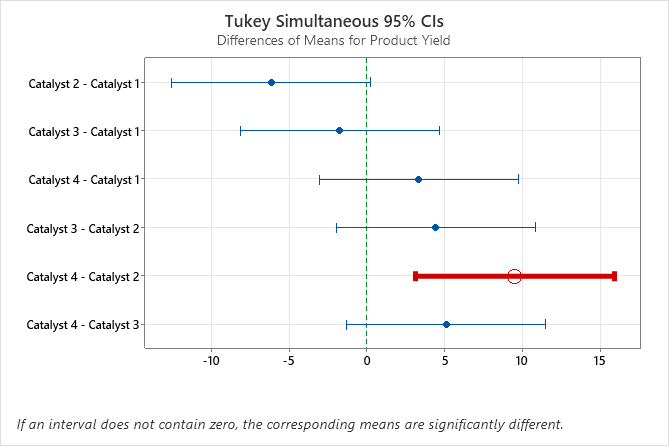
在我们的示例中,包含 Tukey 整体置信区间的图形显示催化剂 2 和 4 的均值间差异的置信区间为 3.114 到 15.886。此范围不包含零,这表明这些均值之间的差异显著。工程师可使用此差值的估计值来确定差异是否实际显著。
相反,其余均值对的置信区间均包含零,这表示差异不显著。
为什么不做一组 T 检验来判别差异?
这是个好的问题,而且经常被问到!此问题的答案与犯错的风险有关,特别是错误地认为存在统计显著差异的风险,这就是我们所说的 Alpha 风险。当我们进行一项检验时,有 5% 的机会我们会说存在差异,而实际上并没有。如果是 4 种催化剂,将进行 6 次 t 检验!
仅凭偶然的机会观察到至少一个显著性结果的概率是多少?
P(至少一个显著性结果)= 1 − P(无显著性结果)
= 1 − (1 − 0.05)6
≈ 0.264
因此,考虑到需要进行 6 次检验,我们有 26% 的机会观察到至少一个显著性结果,即使所有检验实际都不显著。事后检验控制实验误差率;更简单地说,我们希望确保错误地认为任何催化剂对存在显著性差异的机会保持在 5%。这正是 Tukey 检验为我们所做的!
答案是方差分析
使用方差分析使化学工程师能够检验混料以查看结果是否统计意义显著。同样重要的是,还可以使用比较检验确定整组是否存在差异,或者可能差异只存在于组的某部分内。在我们的示例中,只有催化剂 2 和催化剂 4 在产品产量方面在统计上有显著差异。根据这些信息,化学工程师可能会开始查看其他催化剂,以确定哪种催化剂最具成本效益、保质期最长,或最容易获得(因为知道它将产生类似数量的产品)。
为什么您应该了解方差分析
许多工业应用都需要进行实验,其目的是了解组之间是否存在差异。在统计方面,我们考虑一个因子(比如:催化剂类型)并且想了解该因子的各水平(比如:催化剂 1、2、 3 和 4)之间在统计意义上是否有显著差异。当各组的测量是连续的并且满足某些其他假设时,我们使用方差分析来比较各组的平均值。从某种意义上说,“方差分析”这个用词并不恰当,因为我们比较的是各组的均值。然而,通过分析组水平内和组间数据的变化,我们可以确定组均值是否在统计意义上不同。
方差分析检验总体均值(以符号 µ 表示)均相等的原假设。我们将使用样本均值来估计总体均值。如果这个原假设被否定,那么得出的结论是总体均值并不完全相等。
原假设:Ho: µCatalyst 1 = µCatalyst 2 = µCatalyst 3 = µCatalyst 4
简单地说,我们假设各组的均值相等,我们收集证据来证明这一点,即如果我们观察到这些均值之间存在较大差异,则更有可能否定此观点并假设组水平内存在差异。
单因子方差分析示例
想象一下,化学工程师想要比较使用四种不同催化剂的产品产量。 她将催化剂加热与产品一起反应。使用方差分析,工程师可以确定使用不同催化剂的产品产量是否有显著差异。
首先,工程师收集数据,如下所示。
接下来,运行单因子方差分析。
产品产量方差分析的 p 值很小,表明如果原假设成立,即催化剂均值相等,我们观察到这些结果的可能性很小。由于 p 值小于 5% 显著性水平(使用 alpha = 0.05),我们否定原假设。得出的结论是不同催化剂组的平均产品产量不同。
工程师即得知某些组的均值不同。下一个逻辑问题是哪些组的均值不同?
使用 TUKEY 法进行多重比较
虽然通过方差分析,我们知道了某些组的均值不同,但工程师需要进行更深入的比较才能了解到底哪些组的均值不同。Minitab 为此提供了“比较”功能。在我们的示例中,化学工程师使用 Tukey 比较来正式检验组对之间的差异,以了解哪些组对在统计上有显著差异。
Tukey 多重比较检验是多项检验中最保守的检验,可用于确定一组均值中的哪个均值与其他均值不同。方差分析之后使用 Tukey 法(这就是为什么您可能会听到被称为事后检验的方法),可用于为因子水平均值之间的所有成对差异创建置信区间,同时将整体误差率控制在指定的水平。
在我们的示例中,包含 Tukey 整体置信区间的图形显示催化剂 2 和 4 的均值间差异的置信区间为 3.114 到 15.886。此范围不包含零,这表明这些均值之间的差异显著。工程师可使用此差值的估计值来确定差异是否实际显著。
相反,其余均值对的置信区间均包含零,这表示差异不显著。
为什么不做一组 T 检验来判别差异?
这是个好的问题,而且经常被问到!此问题的答案与犯错的风险有关,特别是错误地认为存在统计显著差异的风险,这就是我们所说的 Alpha 风险。当我们进行一项检验时,有 5% 的机会我们会说存在差异,而实际上并没有。如果是 4 种催化剂,将进行 6 次 t 检验!
仅凭偶然的机会观察到至少一个显著性结果的概率是多少?
P(至少一个显著性结果)= 1 − P(无显著性结果)
= 1 − (1 − 0.05)6
≈ 0.264
因此,考虑到需要进行 6 次检验,我们有 26% 的机会观察到至少一个显著性结果,即使所有检验实际都不显著。事后检验控制实验误差率;更简单地说,我们希望确保错误地认为任何催化剂对存在显著性差异的机会保持在 5%。这正是 Tukey 检验为我们所做的!
答案是方差分析
使用方差分析使化学工程师能够检验混料以查看结果是否统计意义显著。同样重要的是,还可以使用比较检验确定整组是否存在差异,或者可能差异只存在于组的某部分内。在我们的示例中,只有催化剂 2 和催化剂 4 在产品产量方面在统计上有显著差异。根据这些信息,化学工程师可能会开始查看其他催化剂,以确定哪种催化剂最具成本效益、保质期最长,或最容易获得(因为知道它将产生类似数量的产品)。
 TA的首页
TA的首页