方差分析在等离子蚀刻中的应用

一、案例背景
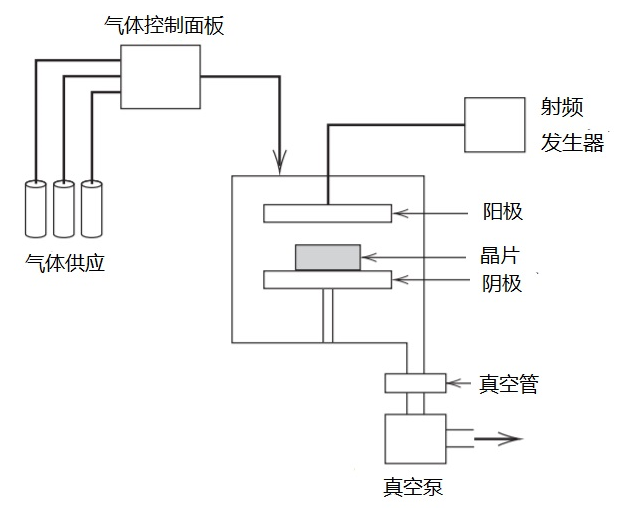
在集成电路的许多生产步骤中，晶片被一层材料(如二氧化硅或某种金属）完全覆盖。通过对掩模的蚀刻有选择性地除去不需要的材料，从而创建电路模板、电互连以及必须扩散的或者金属沉积的区域。等离子蚀刻工序在这个操作中被广泛使用，特别是在几何对象比较小的情况下的应用。下图展示了一种典型的单晶片蚀刻设备的重要特征。特此说明：案例来自蒙哥马利的《实验设计与分析》一书。



射频(RF)发生器提供能源使得电极之间的间隙产生等离子，等离子体的化学种类是由所使用的特定气体决定的。碳氟化合物，比如CF4(四氟甲烷)或C2F6(六氟乙烷)，通常被用在等离子蚀刻上。但是根据应用情况的不同，也常使用其他的气体或混合气体。

工程师要研究这套设备的RF功率设置与蚀刻率间的关系。实验目的是开发工程师要确定RF功率设置是否影响蚀刻率。她选定了气体(C2F6)和间隙(0.80 cm)，想检验RF功率的4个水平：160W，180W，200W和220W。她决定在RF功率的每个水平上检验5个晶片。

这是一个因子水平为4和重复次数为5的单因子实验。这20个试验都是按照随机顺序进行的。



二、分析之前注意事项
一个好的试验设计分析，重点和难点往往不是在如何“分析”它（我相信通过本次案例，您也会借助Minitab做方差分析），而是在于如何“设计”这个试验，如何制定数据收集计划。对于设计得很差的试验，你做不了任何分析。你只能搬出具尸体，找出他的死亡原因。

Fisher曾经说过设计一个试验就像和魔鬼玩机会游戏一样，你无法预测他会使出什么样的高招让你的努力作废。在单晶片蚀刻中亦是如此，为防止未知讨厌变量的影响，随机化试验顺序是必要的，因为实验中讨厌变量的变化也许会超出控制范围。从而损害实验结果。为了方便大家对随机化的理解，请参考如下说明图。



知道了随机化的重要性，哪如何做到随机化呢？我发现很多朋友喜欢按照顺序做试验（先把功率为160的五次试验做完，再做180的，再做200的，最后再做功率为220的五次试验），这就不是我们所说的随机化顺序了。这种按照顺序方式做试验，最后的统计结论往往会变成管理者会议上的争论（我会在后续文章中分享这个故事）。

为了随机化，我们可以在Minitab中执行以下操作：
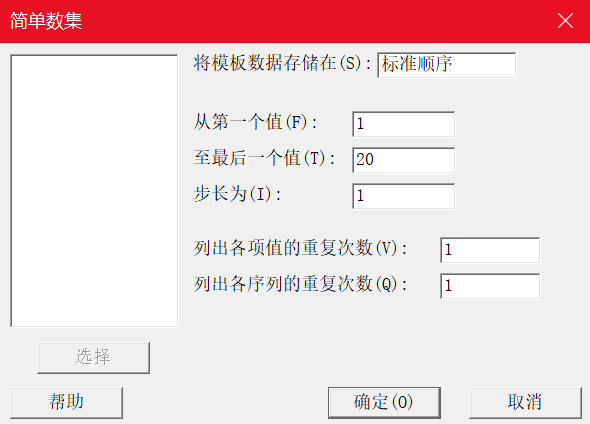
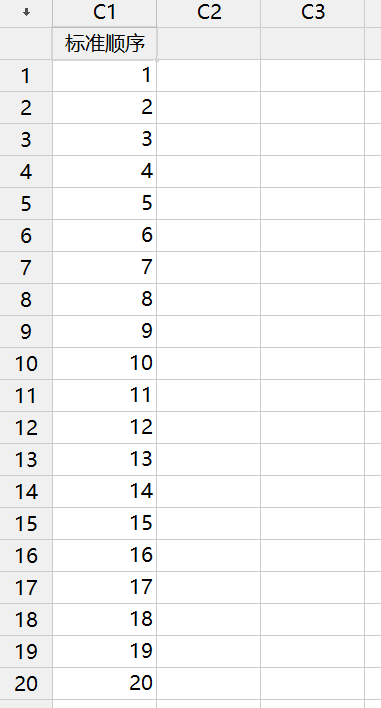
1.首先我们新建一“标准顺序”列，编号从1到20。
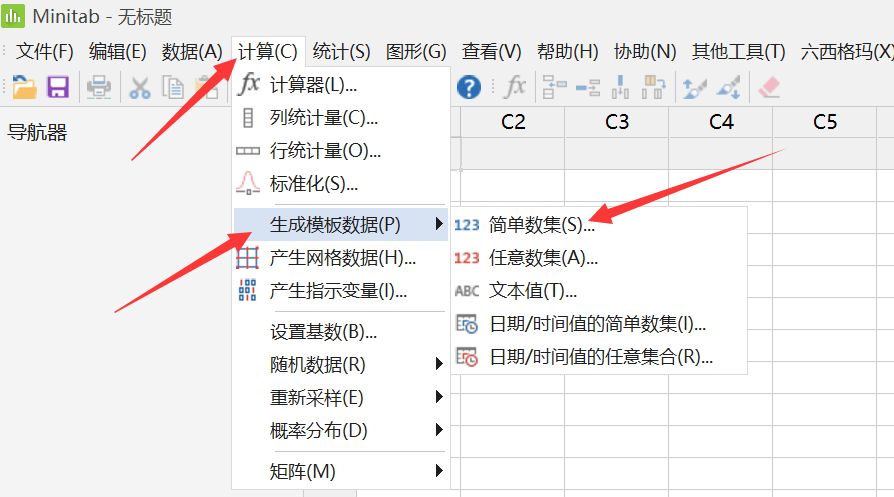
计算-生成模板数据-简单数集







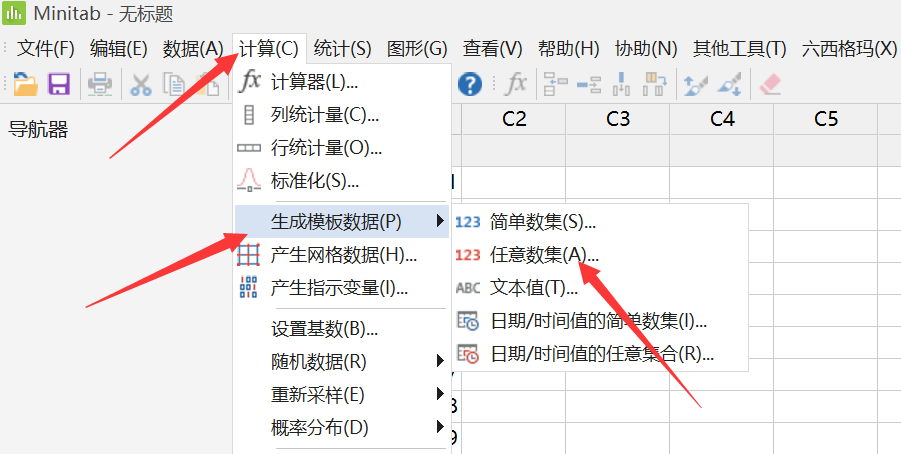
2.计算-生成模板数据-任意数集







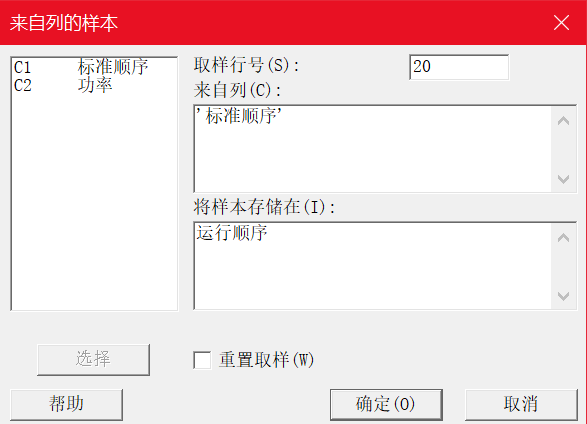
3.计算-随机数据-来自列的样本







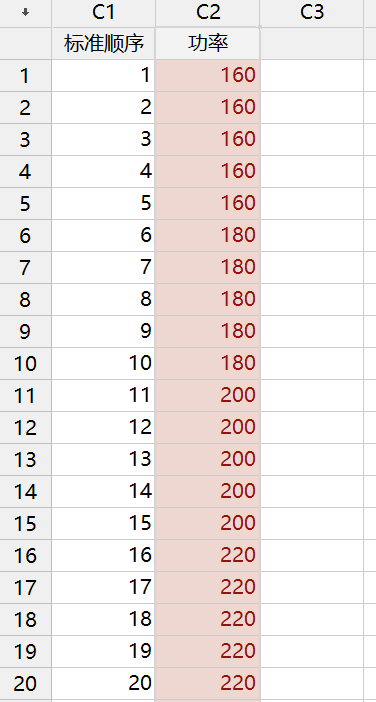
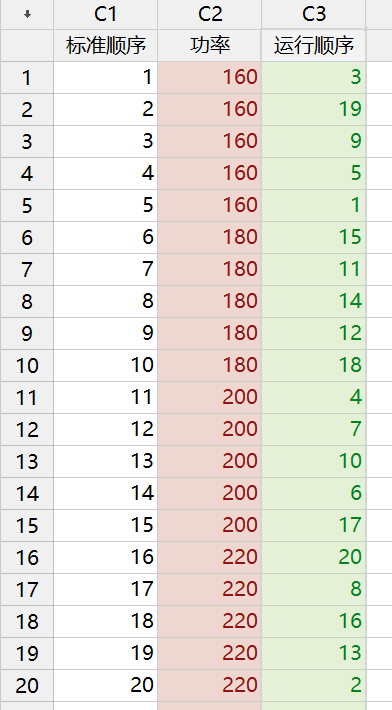
我们按照生成的随机化顺序（C3列运行序）做试验，第一次做功率为160的，第二次做功率为220的……（试验都做了，钱都花了，就不要想着偷懒了）。



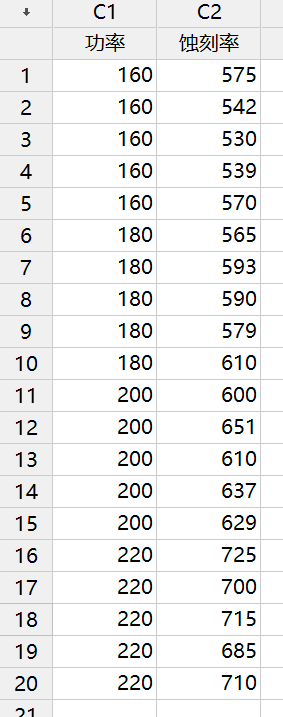
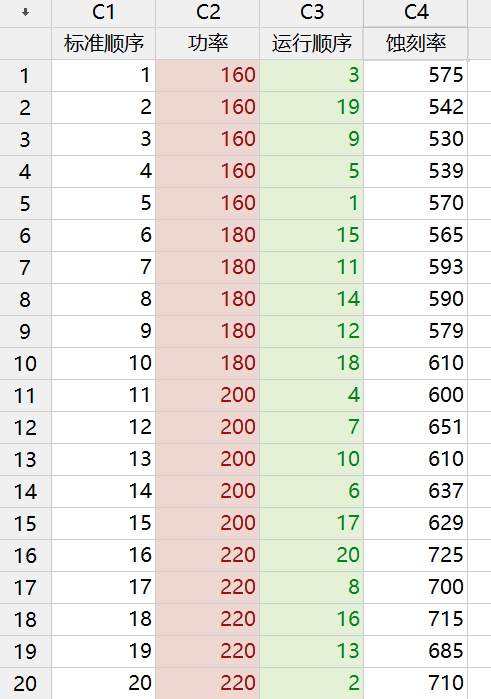
最终，得到以上试验数据（按照随机化顺序做的）。

三、Minitab操作步骤
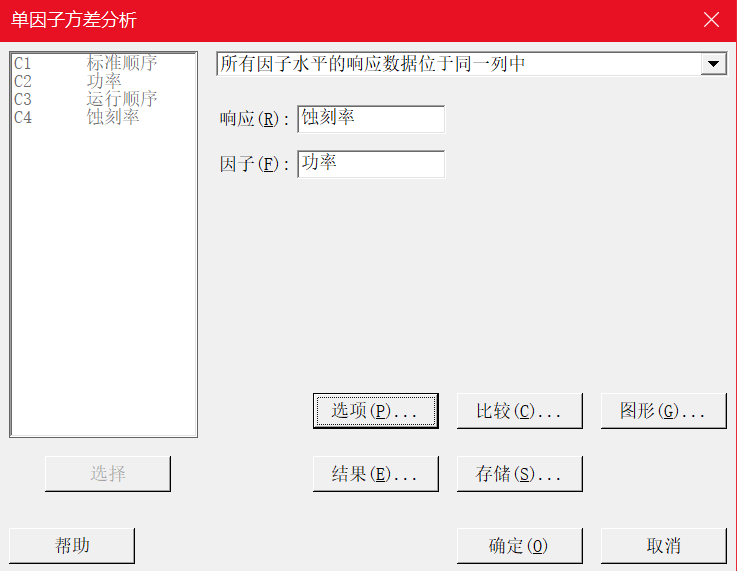
在这里我们是想对单因子（功率）4个水平（160、180、200、220）下的蚀刻率均值做比较，这里我们可以使用方差分析。
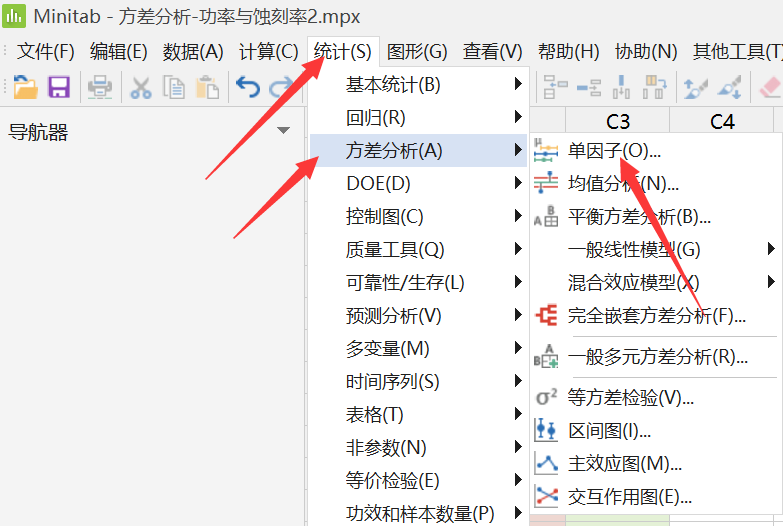
1.路径：统计-方差分析-单因子





2.Minitab结果解释





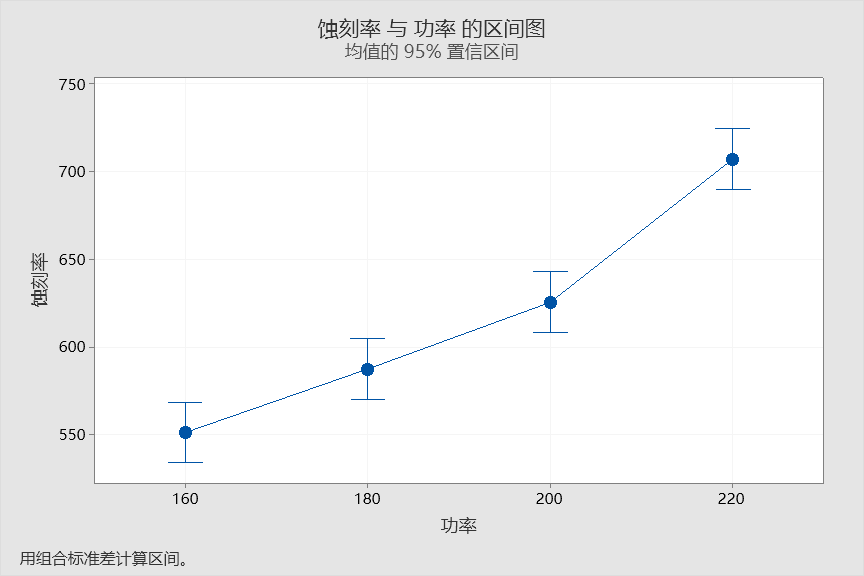
从“方差分析”表中，我们看到检验的P值等于0，小于0.05，故拒绝所有均值都相等的原假设，从而得到4个功率下蚀刻率均值有显著差异的结论。Minitab还同步输出了下面的区间图，从图中可以发现随着功率增大蚀刻率增大。



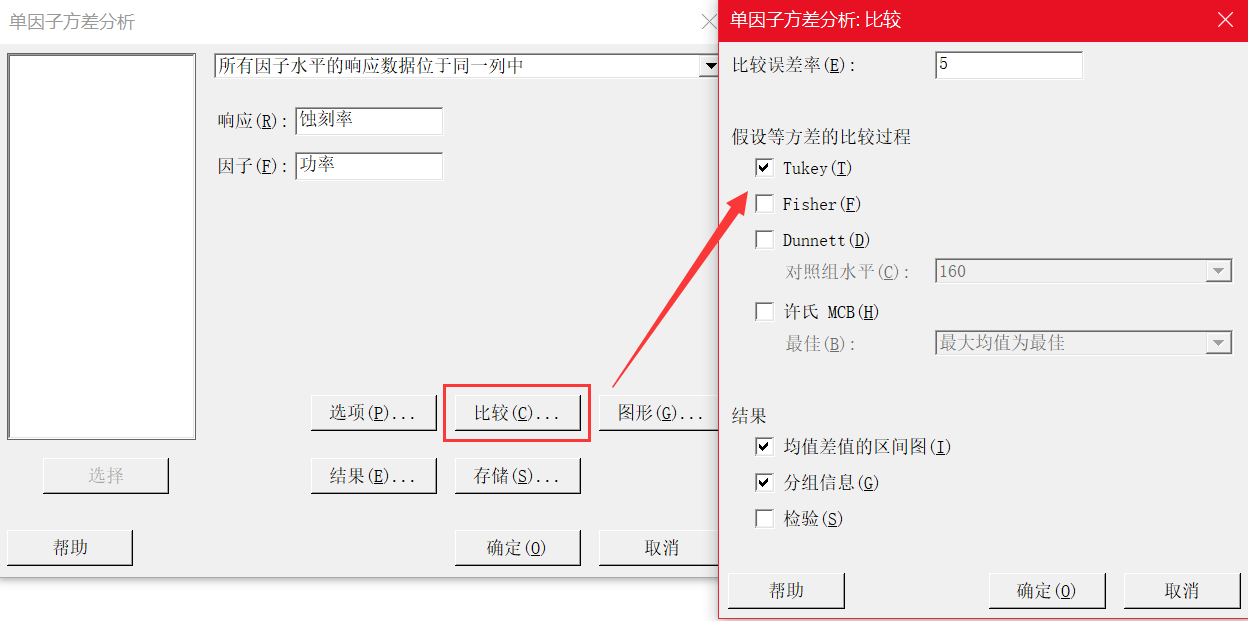
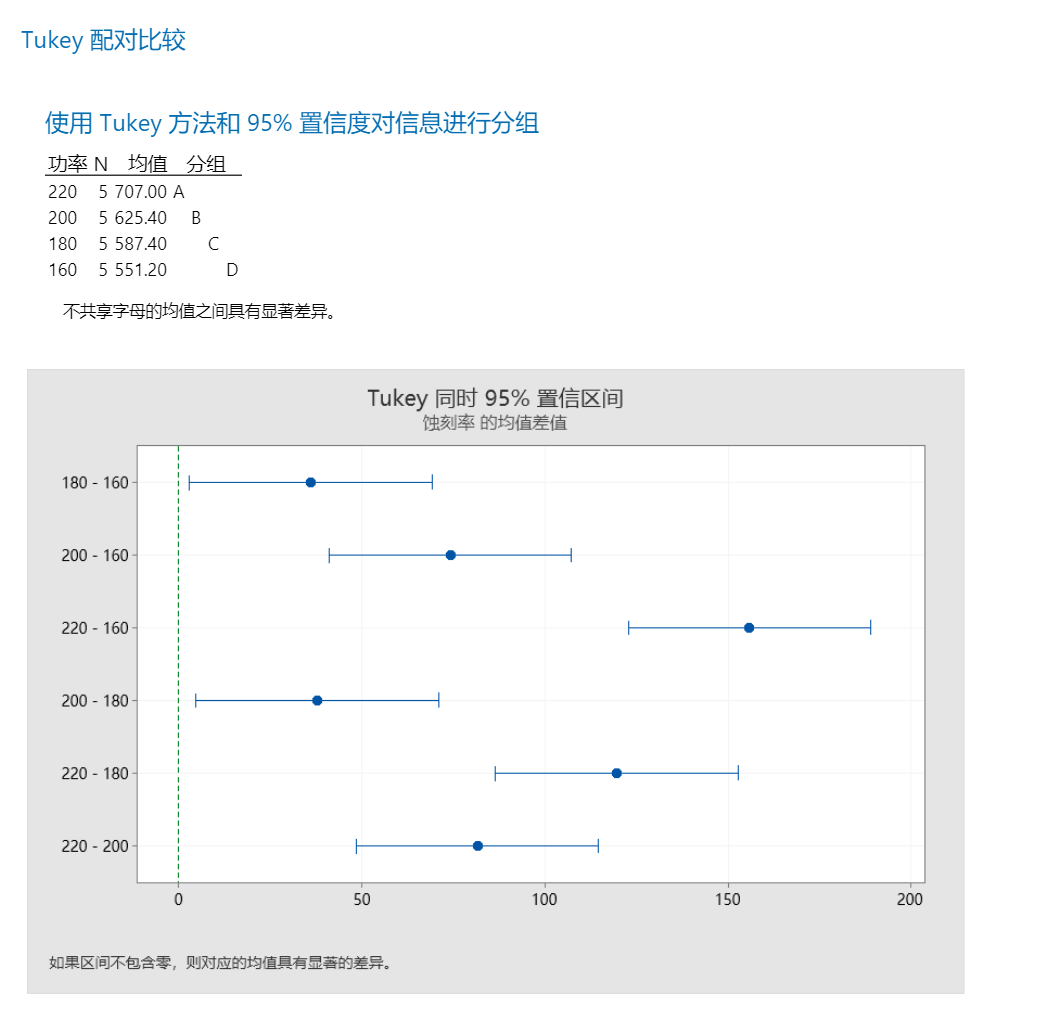
当然，你也可以进一步做多重比较。





四、小结
本篇文章着重向大家强调了试验中“随机化”的重要性以及如何安排随机化试验，我也希望大家能够在后续试验安排做到随机化（我知道，这确实不容易）。一个研究所需要的准备工作远比选择一个统计设计重要得多，统计基于你试验收集的数据，它不会撒谎。但如果试验本身就安排不合理（如没有随机化），利用这个试验获得的数据执行统计分析，那么这时候得到的统计结论有多少能够反映实际生产状况就不得而知了。