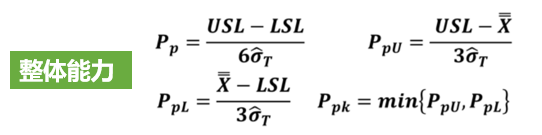过程能力分析04—非正态(非参数方法)

通过此系列文章，目前我们学习了过程能力分析的意义，基于Minitab的正态/非正态数据过程能力分析的思路和方法，其中在非正态数据能力分析中，我们讲了两种方法——转换方法和拟合其他分布方法。文章发布后，果不其然大家又有了新的问题，我们今天先来回答一些问题，再来介绍非正态数据能力分析的另外一种方法——非参数方法。
你有这些疑问吗？

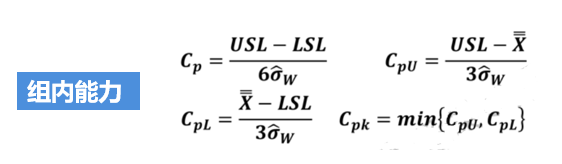
基于前面文章的说明，我们反复强调过程能力分析的一些前提条件（计算Cp/Cpk要求数据满足“独立、正态、MSA合格、稳定”，计算Pp/Ppk只要求数据满足“MSA合格，独立”）。我们还说过，以下公式只适用于正态分布数据。





那么，你有跟下面这位朋友一样的疑问吗？



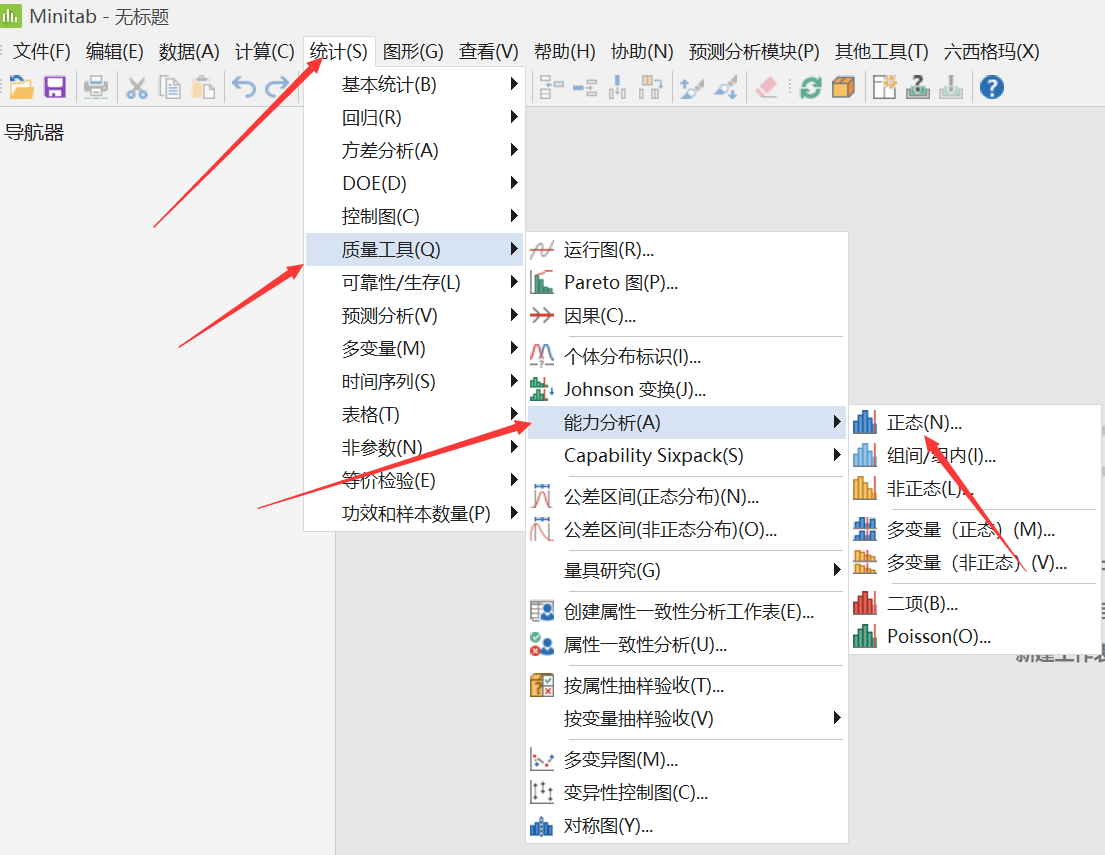
对于这个问题，首先我们要知道，不管是正态数据还是非正态数据都可以计算Ppk，但是拟合分布不同计算结果肯定是有差异。如果数据正态可以按照上面的公式计算，如果非正态我们前面文章介绍了两种方法——转换/拟合其他分布。虽然计算Ppk不需要数据正态，但是做为数据分析人员我们要知道到底选择的正态方法还是非正态方法。直白点说，虽然计算Ppk不要求数据正态，但是我们仍然要在做过程能力分析计算Ppk之前执行正态性检验，只有这样你才知道从Minitab的哪个窗口进入分析。





另外一个问题，也是经常被问到（就我而言，就最少被问过不下20次）。



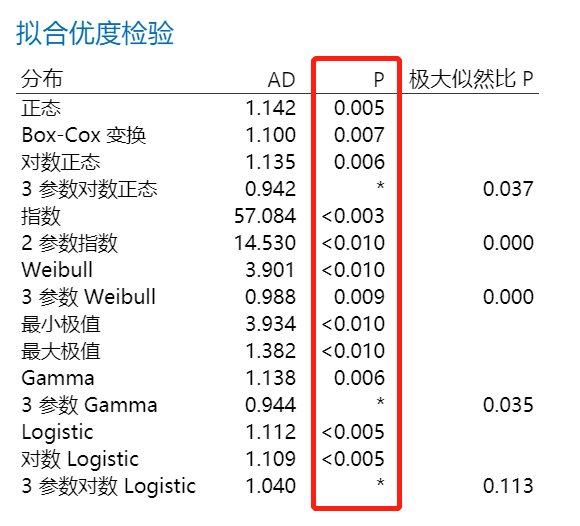
前面文章我们说过，如果数据非正态不要急着转换数据或盲目套其他分布，我们可以先来个“个体分布标识”。但是在“个体分布标识”中我们可能会遇到以下情况——两种变换都不行，14种分布中没有一个能够很好拟合数据。



对于这种情况，我们需要花费更多的精力回到数据搜集的现场做调查，而不是为了得到一个过程能力报告去寻求统计专家的帮助（再高明的专家如果不去现场也只能帮助你猜原因）。

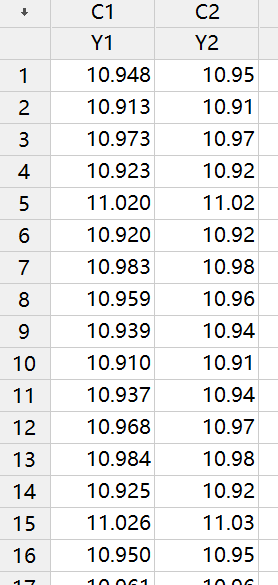
比如像上面的“个体分布标识”输出，为什么找不到合适分布，其实我把数据展示一部分给大家看一下就知道原因了（测量系统分辨力不够或数据经过了修约处理）。



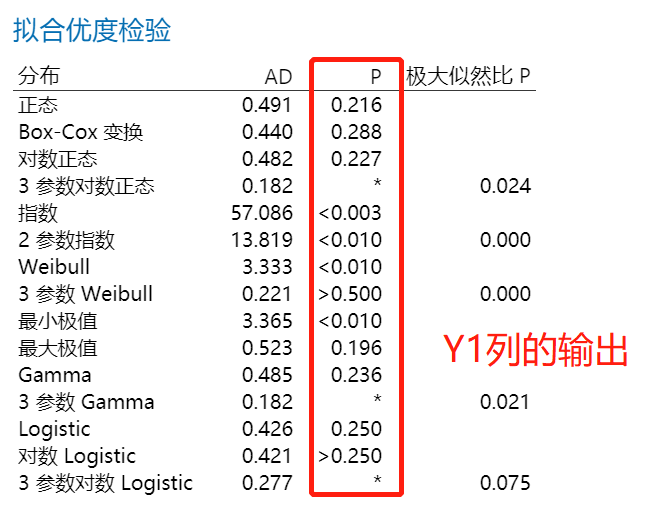
上面的“个体分布标识”是Y2的输出结果，如果我对Y1列执行相同分析呢？



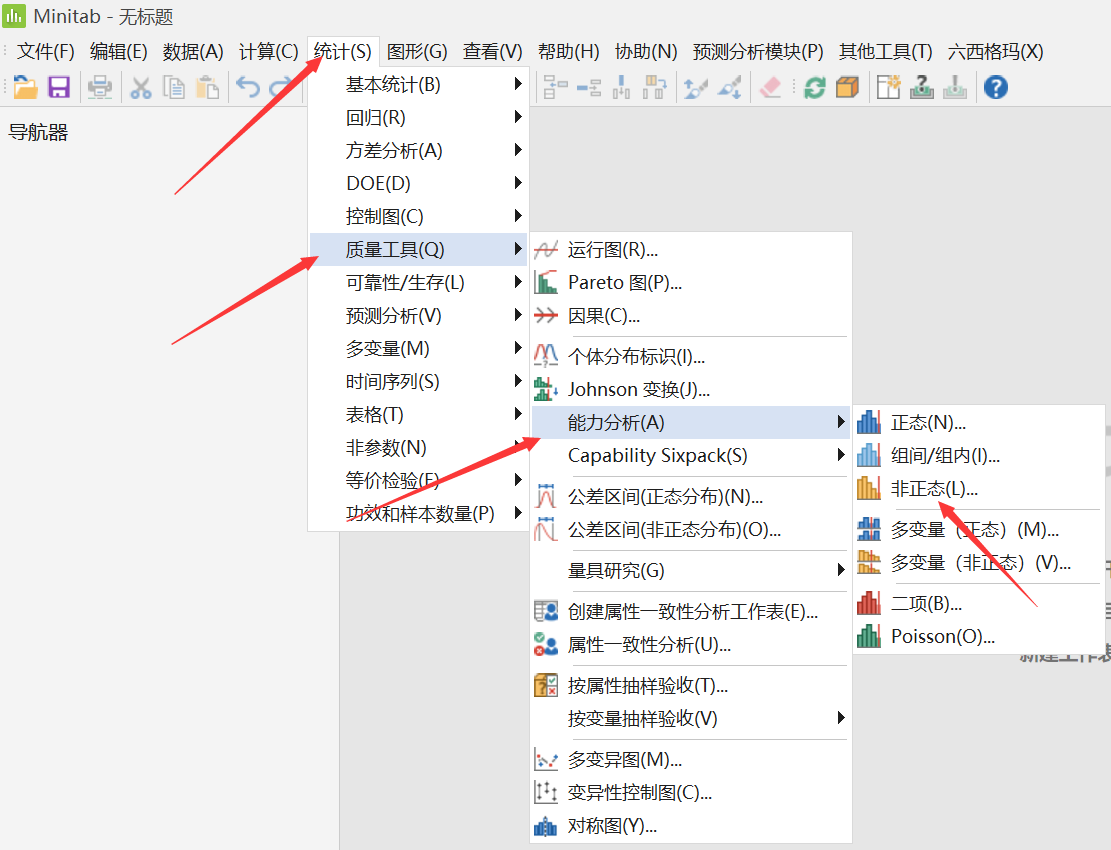
这里我只是展示一种可能找不到合适分布的原因——测量系统分辨力不足，那你的数据又是什么原因导致找不到合格分布呢？这个问题别人无法回答，需要你去现场找答案。那如果我所有怀疑的原因都找了一圈结果还是没有发现问题出在哪里，那可不可以计算过程能力呢？这时候如果你的数据量比较大的话（最好1000以上），我们还有一种方法可以来计算过程能力——非参数方法。这种方法不需要知道拟合分布，但要求样本量比较大。
 
非参数方法

非参数方法计算过程能力的核心逻辑跟前面介绍的拟合其他分布是一样的。



因为找不到合适拟合分布，所以这里的分位数计算就不能用之前的方法了，在这里你可以手算也可以利用 Minitab自带的宏命令来计算这些分位数。



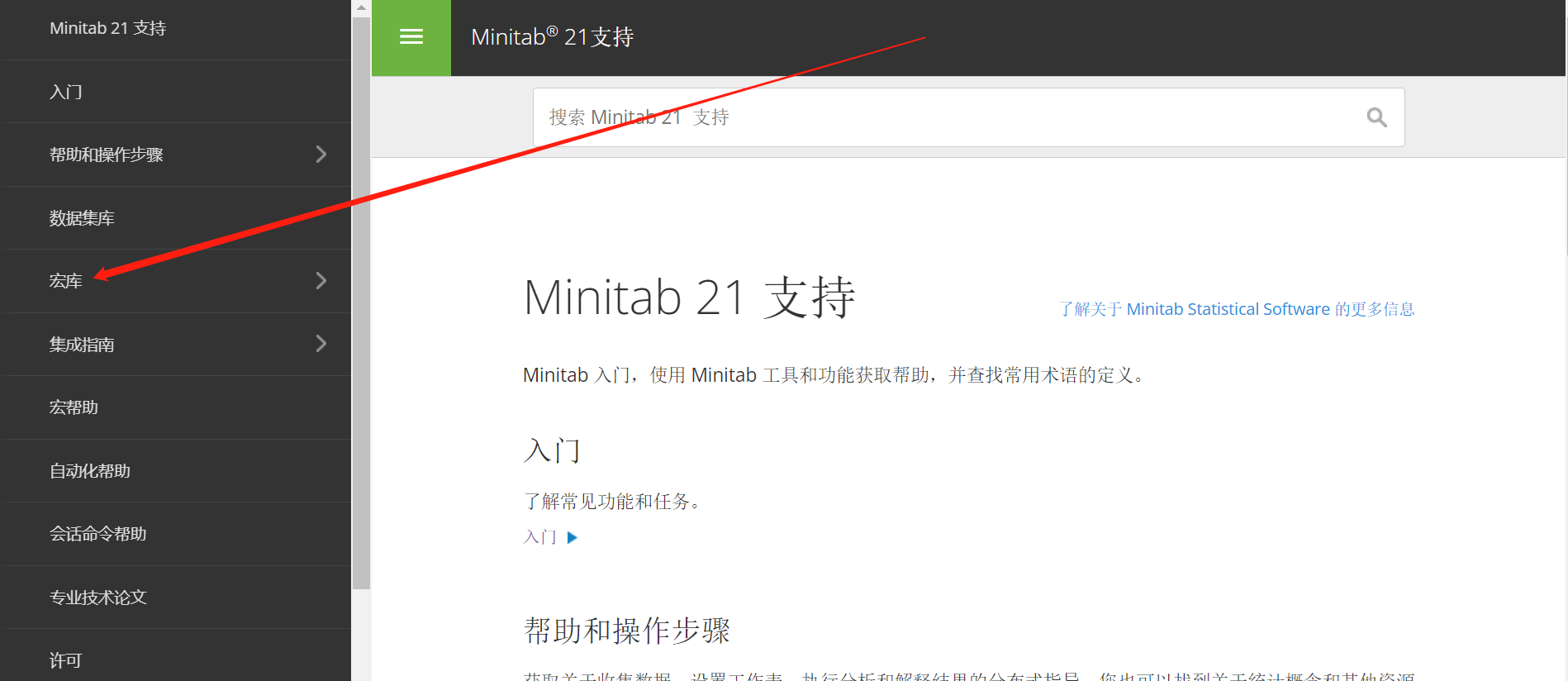
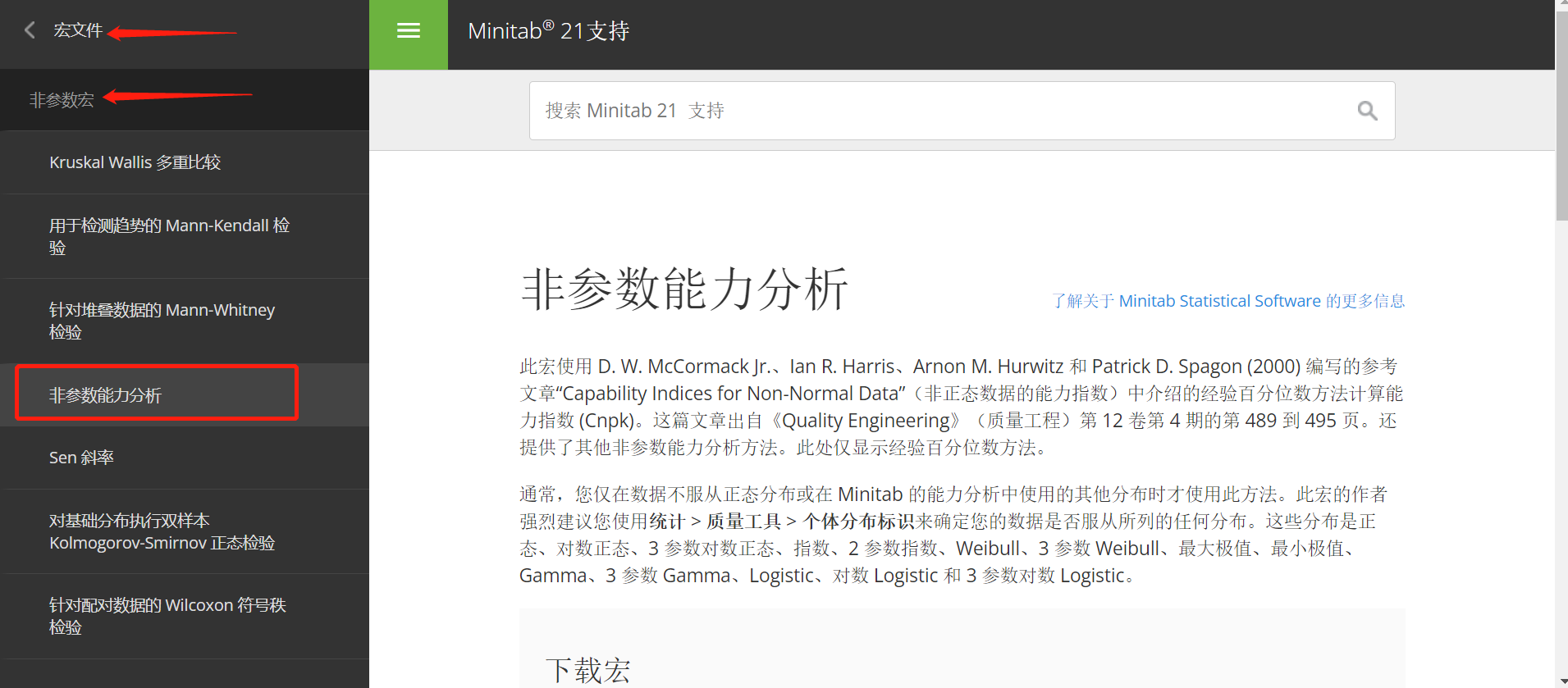
点击“帮助”菜单，我们可以在帮助文档中找到相应的宏命令。







把这个宏命令下载下来，运行之前请阅读仔细阅读帮助中说明，尤其要注意把宏放到指定的位置。