假设检验的功效和样本数量

在假设检验中，我们会使用样本中的数据来描绘有关总体的结论。首先，我们会进行假设，这被称为原假设（以 H0 表示）。当您进行原假设时，您也需要定义备选假设 (Ha)，其与原假设正相反。样本数据将用于判断 H0 是否可以被否定。如果其被否定，则统计结论将认为备选假设 Ha 正确。 

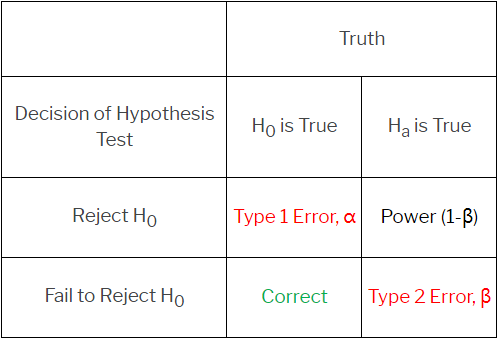
请记住这一检验的功效，或是在原假设不正确时，原假设被否定的可能性。

它可以解释为“检验在应该拒绝原假设时拒绝原假设的能力”。如果原假设不正确，则有很高概率拒绝原假设是很有意义的。功效与类型 2 的错误相关（功效 = 1 - 类型 2 错误），请见下表。类型 2 错误是当备选假设正确时不拒绝原假设的概率。因此，确保有足够高的功效，才能保证类型 2 错误较低或“可以接受”。确保检验有足够功效的一种常用方法是收集足够的数据，因为功效的计算取决于样本数量等因子。样本数量越大，功效越高。换言之，未能收集足够的数据将导致低功效和大量类型 2 错误。 



最重要的是要找到合适的样本数量。显而易见，未能收集足够的数据会导致更多的类型 2 错误。但是，收集“过多”的数据也会增加类型 1 错误，因为检验的功效会更高。因此，该检验可能会检测到与假设值的微小差异，即使该差异可能没有任何实际意义，尤其是与抽样成本有关时。检验功效的计算应当基于实际意义。 
MINITAB具有通过多种不同统计检验计算功效的功能

在下列示例中，分析人员在 Minitab 中通过单比率检验和单样本 t 检验，进行了功效和样本数量分析。 

单比率检验样本数量

考虑将产品分类为好或差的制造过程，其中有 1% 的不良品率。如果不良品率上升至 3%，则会对整个组织造成严重的成本问题。他们需要确定合适的样本数量，以满足：类型 I 错误率为 0.05，检验功效为 0.80，以检测出不良品率从 1% 上升至 3% 或更高。 
因为分析人员对不良品率研究感兴趣，他们使用了单比率检验。原假设和备选假设是： 
Ho: P = 0.01 
Ha: P > 0.01 
其中 P 为实际缺陷比率。
为了找出需要多少数据点才能达到至少0.8的功效，分析人员在 Minitab 中进行了单比率检验的功效和样本数量分析。 



单样本 t 检验的样本数量

将产品分类为好或差很简单，但会损失很多信息。将好产品视为在 5 到 10 之间。假如有 2 个单元测得的数值为 4.9 和 10.01，并因而归入差的分类。假如有另外 2 个单元测得的数值为 2.3 和 14.1，并因而归入差的分类。请注意，如果只是简单的区分好和差，这两种情况是相同的。因此，如果测量产品质量特征是可行的，那么分析人员应该记录质量特征的实际值，并使用记录的数据 – 无需转换为好和差。单样本 t 检验可以用于检验总体的均值是否与目标一致。如果样本数据的均值接近“目标”，则该过程可能运行良好。如果均值不接近目标，则可能生产出缺陷产品。 
 
例如，假设该产品特征为特定目标的孔直径。分析人员可以测量每个产品上的孔直径，并使用单样本 t 检验将均值与目标值进行比较，而不是检查 236 个产品以确定孔是否符合规格。 

为了找出需要多少数据点来检测至少 80% 功效的过程均值中的 1 西格玛偏移，分析人员在 Minitab 中对一个单样本 t 检验进行功效和样本数量分析。 



计算的样本数量仅为 10。这意味着如果分析人员希望确定目标的偏离均值是否超过了 1 西格玛，则他们需要进行 10 个单位的单样本 t 检验，以获得至少 80% 的功效。 

为什么会有这么大的区别？

属性数据的假设检验需要大量样本，因为在收集数据时没有获取详细信息。另一方面，连续数据的假设检验只需较少的样本数量，因为其获取并使用了产品的详细信息。该理论不仅适用于功效。属性数据需要大量样本以用于置信区间、属性一致性分析、控制图和能力分析。 

总之，重要的是进行具有足够功效的假设检验，以提供合理的机会来检测差异。功效与样本数量直接相关。Minitab 具有计算多种不同假设检验（包括试验设计）的功效的功能。 

本文最初出现在Minitab博客上。