等价检验 VS 显著性检验
传统显著性检验用于推断样本所代表的总体均值是否相等,它的检验假设为样本来自同一总体(即总体均值相等)。在应用中,显著性检验结果不能评价差别的大小,也不能说明差别是否有实际意义,所谓差别显著是指在统计学理论上认为样本来自不同的总体。另外显著性检验在均值差异性比较中也存在一定的局限性,下面我们以双样本t检验为例来说明。
显著性检验的局限性
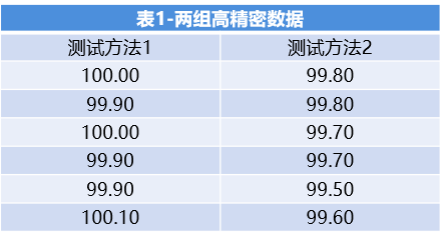
我们看到下表1中两种测试方法得到的数据,希望比较两种测试方法得到的结果是否一致(等效)。
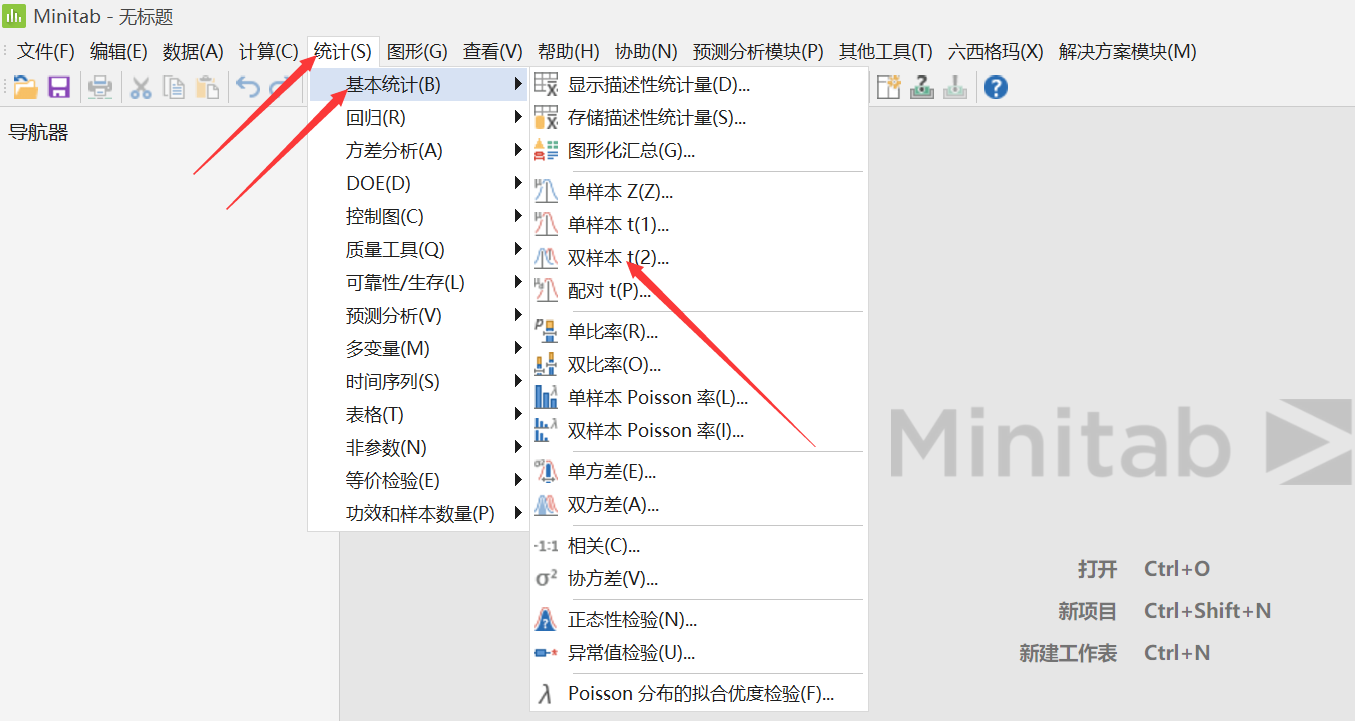
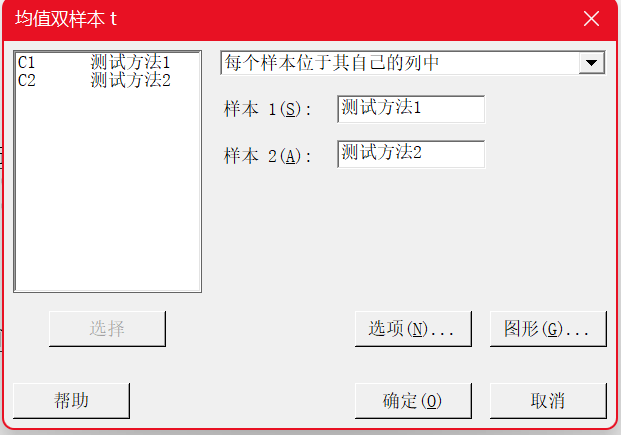
可能首先想到的方法就是用双样本t检验,我们来试试看(前提条件验证略)。
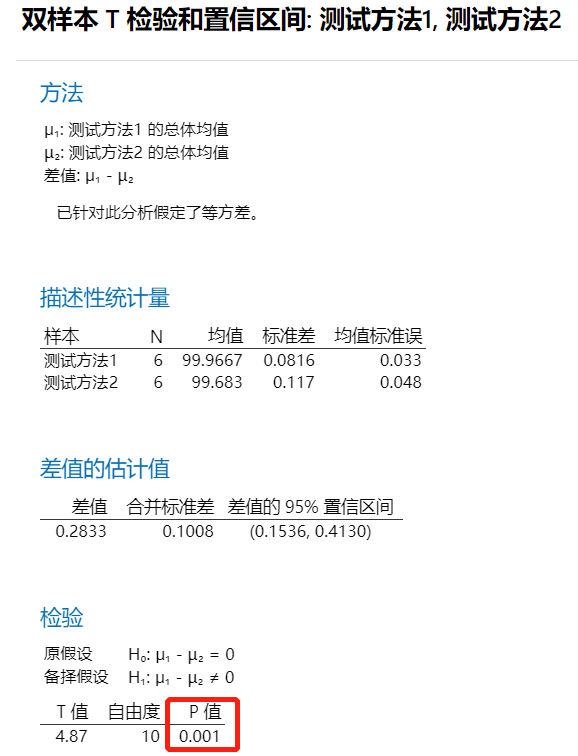
双样本t检验的结果显示,P=0.001<0.05,所以我们得到的结论是:两种测试方法的结果是有显著性差异的。拒绝是有说服力的,所以我们也不用担心犯第二类错误。
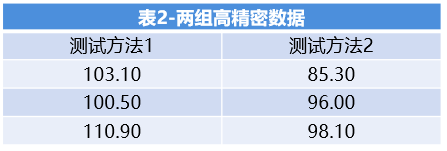
现在我们再来看看下表2中两种测试方法的数据,也想来比较有没有显著性差异。
同理,我们也来执行双样本t检验(前提条件验证略),得到如下结果。
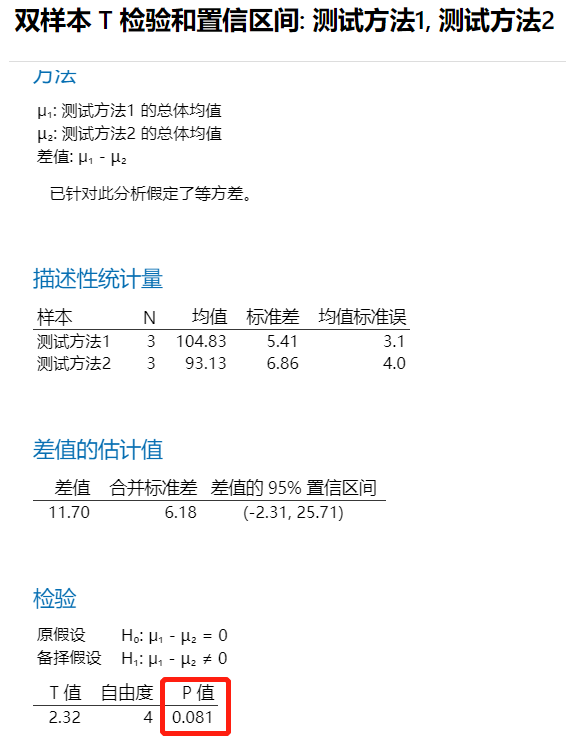
双样本t检验的结果显示,P=0.081>0.05,所以我们得到的结论是:两种测试方法的结果无显著性差异的,即不拒绝原假设。不拒绝是没有说服力的,可能是样本量不够导致的(建议做功效与样本量的计算)。
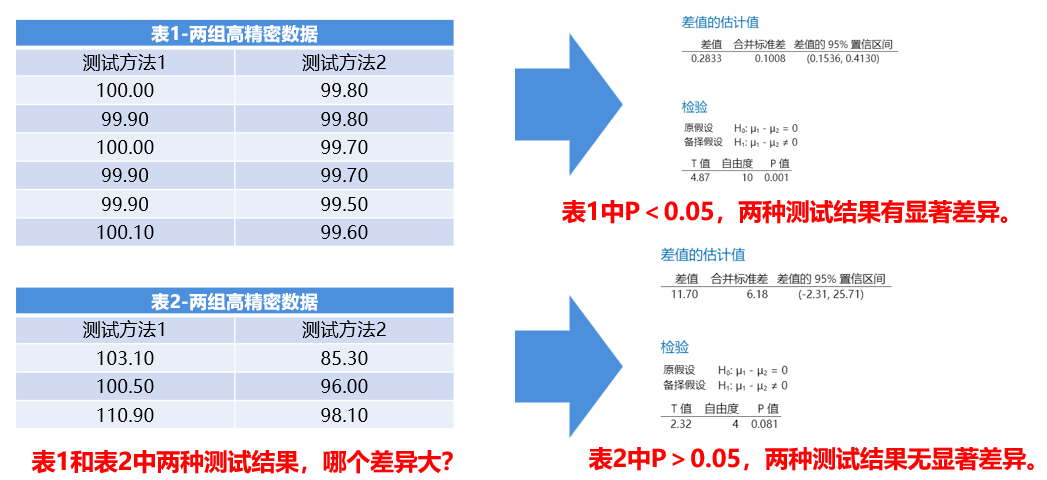
基于以上分析,总结如下:
但是,如果你仔细去看一看表1和表2中的数据,有没有发现表1中两种测试方法结果差异比较小(但双样本t检验结果P=0.001<0.05),表2中两种测试方法结果差异比较大(但双样本t检验结果P=0.081>0.05),注意,这不是错觉,这是t检验本身存在的局限性。
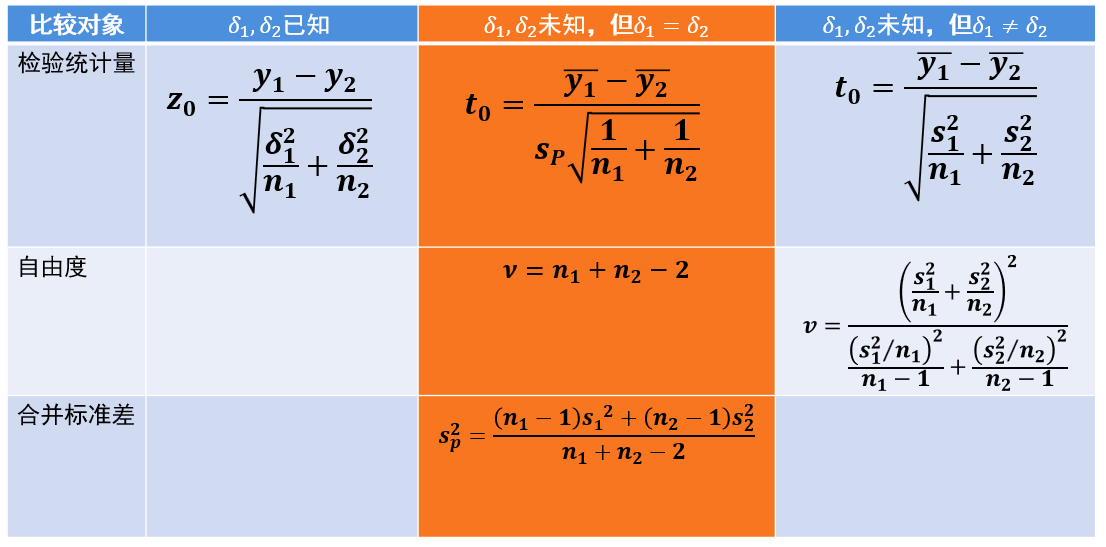
为什么这么说,我们以表2中数据(两总体标准差未知但相等)为例来看看t检验的基本原理。
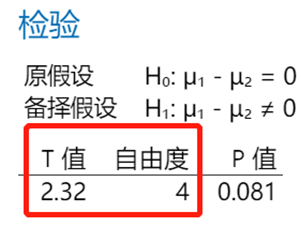
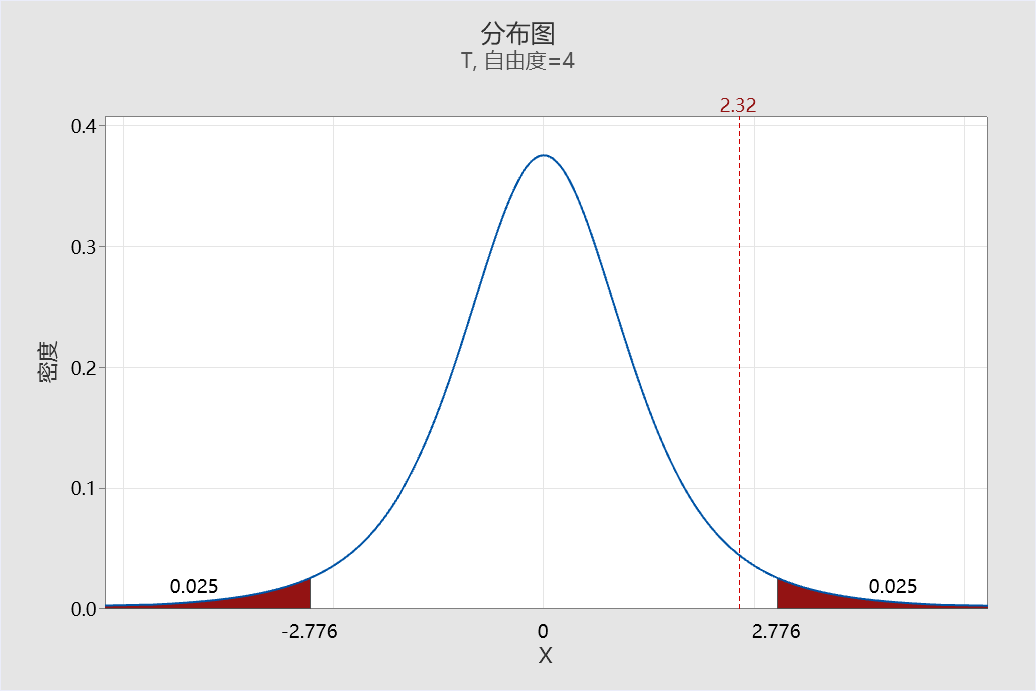
T=2.32小于拒绝域临界值2.776,及检验统计量T落在非拒绝域(白色区域),故不拒绝原假设。换句话说,如果想拒绝原假设(得到两种测试方法有显著差异的结论),就需要检验统计量T值(绝对值)足够大,大到超过2.776,那么怎么做才能实现呢?通过后台公式我们能发现只需要:样本量足够大且/或合并标准差SP足够小。
其实这是一个有悖逻辑的发现,因为如果真的如此的话,那我以后直接选择摆烂不就可以吗(样本量少抽一点,测量变异搞大点,这样越不容易得到有显著差异)。
等价检验
从功能和实用意义上来讲,产品之间存在微小差异并不总是十分重要。例如,在200 mg的药物剂量中,相差1mg不会产生任何实际效应,那如果我想证明药物剂量不同对疗效是相同的或相近的,又该如何去验证呢?可不可以用显著性检验的方法(如t检验)?
显著性检验确定备择假设的方法是“想证明什么结论就把它放在备择假设上”,那能否把相等的结论放在备择假设上,如H0:μ≠μ0, H1: μ=μ0很遗憾,统计学中不可能处理这种“原假设是某个范围,而备择假设只是一个单点”的情况,只能处理备择假设为
H1:|μ-μ0|<△
H1: μ1<μ<μ2
其中μ1=μ0-△,μ2=μ0+△
这类检验问题称为等价检验(equivalence test)问题,也称等效性检验问题。其中(μ1,μ2)称为等价区间。它的原假设和备择假设为:
H0:μ<μ1或μ>μ2 H1:μ1≤μ≤μ2
等价检验实际上是双单侧假设检验(TOST),当左右两边的原假设同时被拒绝时才能认为原假设不成立。
等价检验 VS 显著性检验
等价检验与显著性检验比较如上图,下面我们通过一个具体案例来说明一下(案例来自于蓝皮书第三版P161)。
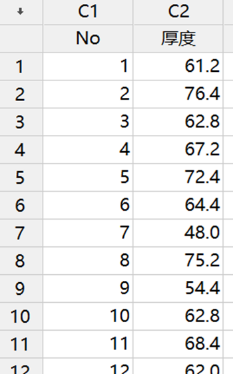
示例:在焊接电路板的过程中,焊锡膏的涂抹厚度是关键的控制量之一。工艺标准要求涂抹厚度的均值是60微米,均值偏差在5微米内。现在收集了25个焊点上的焊锡膏涂抹厚度。我们希望验证,涂抹厚度均值是60微米吗?涂抹厚度均值是落在(55,65)之内吗?
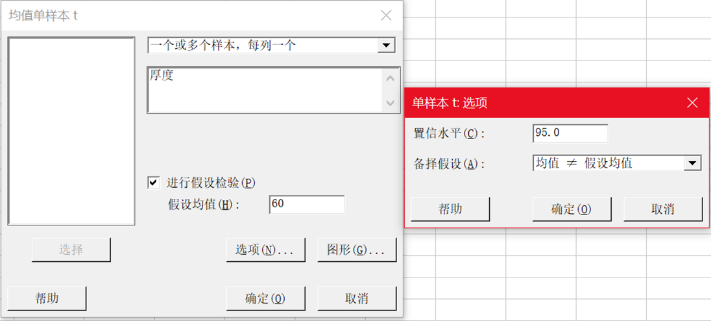
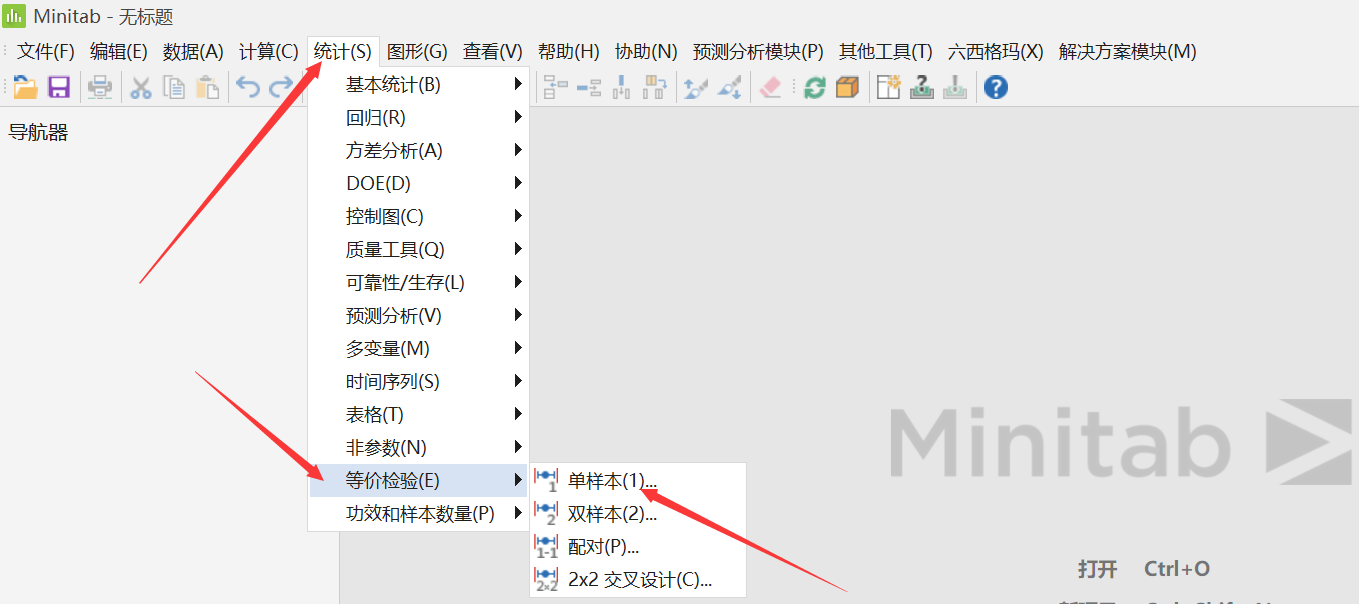
我们先来看看如果是用显著性检验(单样本t检验)会得到什么结果。
由于P值为0.111,因此无法拒绝原假设,也就是说没有充分的理由否认焊锡膏涂抹厚度均值为60。但“不否认”还不是明确的说明“均值就是60微米”的有说服力的结论。如果需要进一步确定“均值就是60微米”,或者更进一步判断其均值是否落入(55,65),则只能使用单样本等价检验方法(注意:即使是等价检验对于备择假设只是一个单点也是无能为力的)。
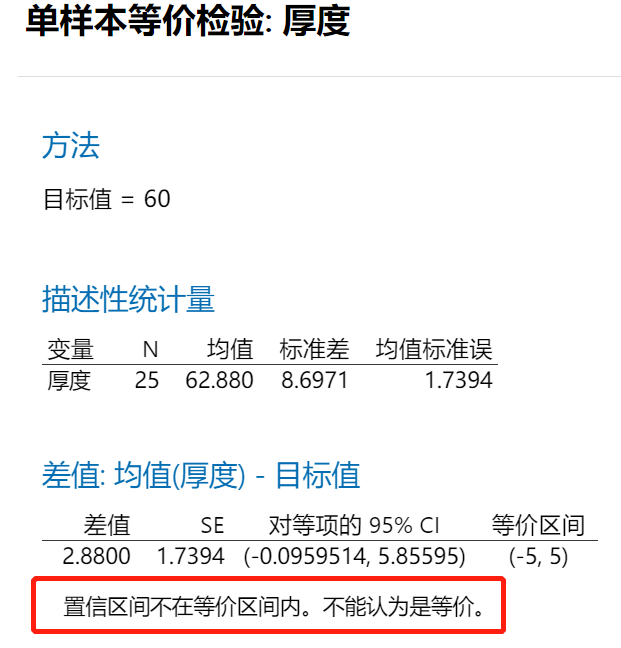
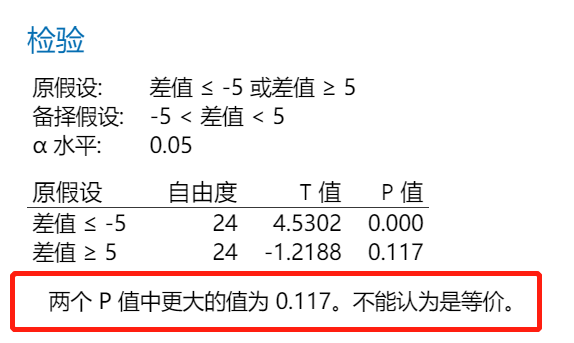
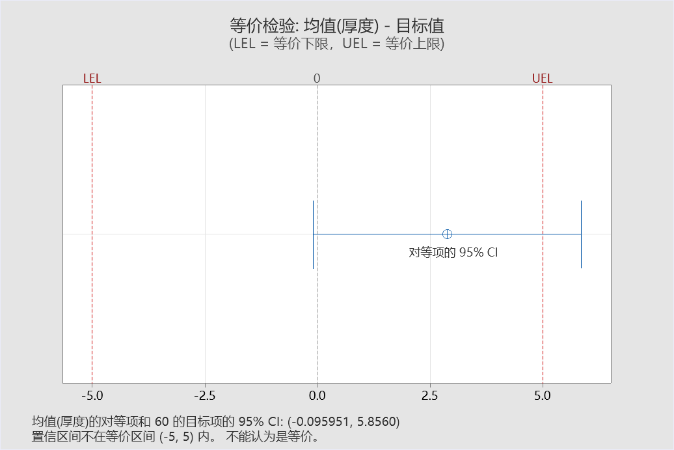
正如Minitab告诉你的,不能认为是等价的,即焊锡膏涂抹厚度均值可以认为是60微米,但未落在(55,65)之内,即精确度未达到误差小于5微米的水平。
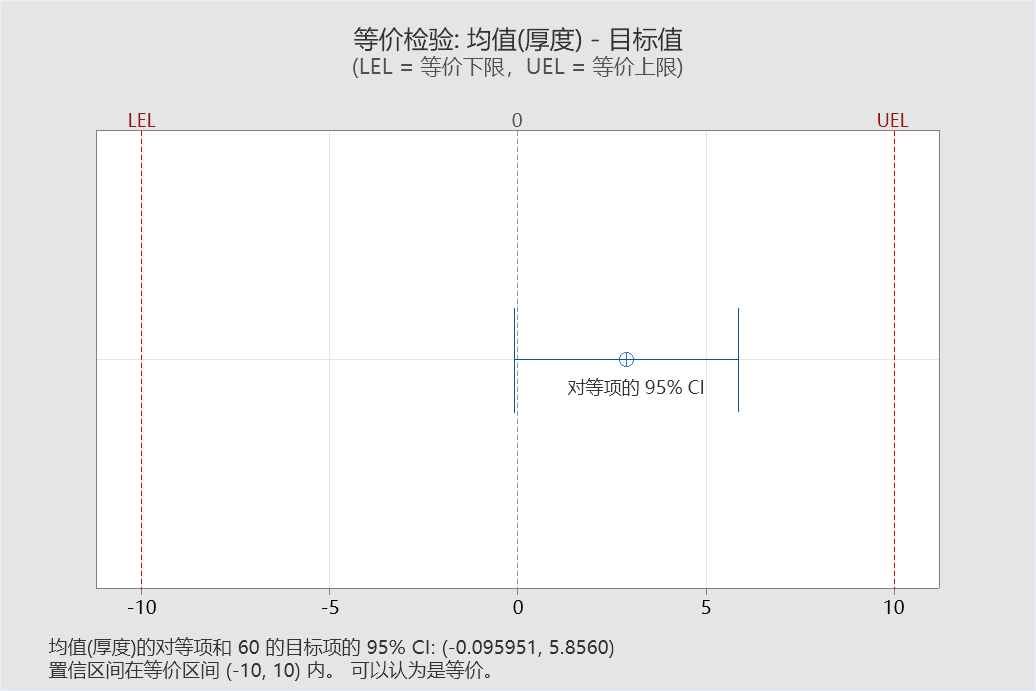
那如果允许误差放大些,比如说(50,70),结果就可以认为是等价的了。
请注意,我在这里不得不说明一下,千万不要说为了得到等价的结论而去改等价区间,我在这里修改只是为了说明问题,我们在实际工作一定是要事先指定好等价区间范围(防止扯皮)。
小结
要在等价检验和标准t检验之间进行选择,请考虑您希望证明或说明的内容。如果您希望证明两个均值相等或者证明均值等于目标值,而且您可以确切地定义在所属领域中属于重要差值的差值大小,则您可能希望使用等价检验,而不是标准t检验。
显著性检验的局限性
我们看到下表1中两种测试方法得到的数据,希望比较两种测试方法得到的结果是否一致(等效)。
可能首先想到的方法就是用双样本t检验,我们来试试看(前提条件验证略)。
双样本t检验的结果显示,P=0.001<0.05,所以我们得到的结论是:两种测试方法的结果是有显著性差异的。拒绝是有说服力的,所以我们也不用担心犯第二类错误。
现在我们再来看看下表2中两种测试方法的数据,也想来比较有没有显著性差异。
同理,我们也来执行双样本t检验(前提条件验证略),得到如下结果。
双样本t检验的结果显示,P=0.081>0.05,所以我们得到的结论是:两种测试方法的结果无显著性差异的,即不拒绝原假设。不拒绝是没有说服力的,可能是样本量不够导致的(建议做功效与样本量的计算)。
基于以上分析,总结如下:
但是,如果你仔细去看一看表1和表2中的数据,有没有发现表1中两种测试方法结果差异比较小(但双样本t检验结果P=0.001<0.05),表2中两种测试方法结果差异比较大(但双样本t检验结果P=0.081>0.05),注意,这不是错觉,这是t检验本身存在的局限性。
为什么这么说,我们以表2中数据(两总体标准差未知但相等)为例来看看t检验的基本原理。
T=2.32小于拒绝域临界值2.776,及检验统计量T落在非拒绝域(白色区域),故不拒绝原假设。换句话说,如果想拒绝原假设(得到两种测试方法有显著差异的结论),就需要检验统计量T值(绝对值)足够大,大到超过2.776,那么怎么做才能实现呢?通过后台公式我们能发现只需要:样本量足够大且/或合并标准差SP足够小。
其实这是一个有悖逻辑的发现,因为如果真的如此的话,那我以后直接选择摆烂不就可以吗(样本量少抽一点,测量变异搞大点,这样越不容易得到有显著差异)。
等价检验
从功能和实用意义上来讲,产品之间存在微小差异并不总是十分重要。例如,在200 mg的药物剂量中,相差1mg不会产生任何实际效应,那如果我想证明药物剂量不同对疗效是相同的或相近的,又该如何去验证呢?可不可以用显著性检验的方法(如t检验)?
显著性检验确定备择假设的方法是“想证明什么结论就把它放在备择假设上”,那能否把相等的结论放在备择假设上,如H0:μ≠μ0, H1: μ=μ0很遗憾,统计学中不可能处理这种“原假设是某个范围,而备择假设只是一个单点”的情况,只能处理备择假设为
H1:|μ-μ0|<△
H1: μ1<μ<μ2
其中μ1=μ0-△,μ2=μ0+△
这类检验问题称为等价检验(equivalence test)问题,也称等效性检验问题。其中(μ1,μ2)称为等价区间。它的原假设和备择假设为:
H0:μ<μ1或μ>μ2 H1:μ1≤μ≤μ2
等价检验实际上是双单侧假设检验(TOST),当左右两边的原假设同时被拒绝时才能认为原假设不成立。
等价检验 VS 显著性检验
等价检验与显著性检验比较如上图,下面我们通过一个具体案例来说明一下(案例来自于蓝皮书第三版P161)。
示例:在焊接电路板的过程中,焊锡膏的涂抹厚度是关键的控制量之一。工艺标准要求涂抹厚度的均值是60微米,均值偏差在5微米内。现在收集了25个焊点上的焊锡膏涂抹厚度。我们希望验证,涂抹厚度均值是60微米吗?涂抹厚度均值是落在(55,65)之内吗?
我们先来看看如果是用显著性检验(单样本t检验)会得到什么结果。
由于P值为0.111,因此无法拒绝原假设,也就是说没有充分的理由否认焊锡膏涂抹厚度均值为60。但“不否认”还不是明确的说明“均值就是60微米”的有说服力的结论。如果需要进一步确定“均值就是60微米”,或者更进一步判断其均值是否落入(55,65),则只能使用单样本等价检验方法(注意:即使是等价检验对于备择假设只是一个单点也是无能为力的)。
正如Minitab告诉你的,不能认为是等价的,即焊锡膏涂抹厚度均值可以认为是60微米,但未落在(55,65)之内,即精确度未达到误差小于5微米的水平。
那如果允许误差放大些,比如说(50,70),结果就可以认为是等价的了。
请注意,我在这里不得不说明一下,千万不要说为了得到等价的结论而去改等价区间,我在这里修改只是为了说明问题,我们在实际工作一定是要事先指定好等价区间范围(防止扯皮)。
小结
要在等价检验和标准t检验之间进行选择,请考虑您希望证明或说明的内容。如果您希望证明两个均值相等或者证明均值等于目标值,而且您可以确切地定义在所属领域中属于重要差值的差值大小,则您可能希望使用等价检验,而不是标准t检验。
 TA的首页
TA的首页