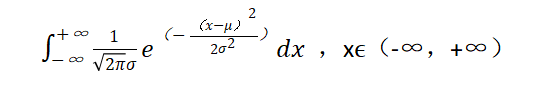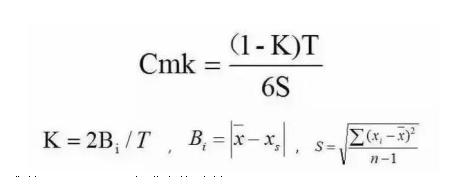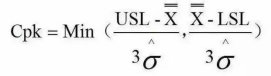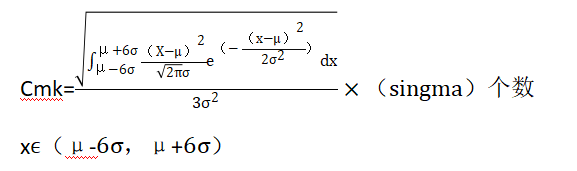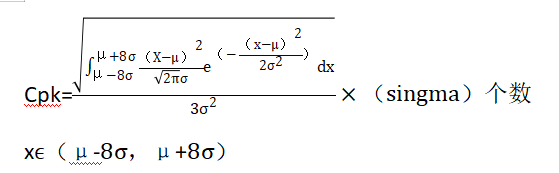扭矩精度西格玛与Cmk Cpk的关系研究
扭矩精度西格玛与Cmk Cpk的关系研究
黄飞鸿
(宁波安德路工业自动化设备有限公司)
摘要:
随着日益规范化的设备使用过载中,对精度的标注更加规范化,以西格玛和精度范围作为精度的标准,从而衍生出满足精度标准的Cmk和Cpk的规律和计算方式的推算。以下内容以深圳艾而特工业自动化设备有限公司的ACT型螺丝刀作为范例进行演示。
关键词:精度;Cmk;Cpk;西格玛;
1 总结性描述
1.1背景
1.目前螺丝刀的进度在3西格玛±5%的精度情况下,在手持螺丝刀时候,扭力的测试数据很难计算Cmk1.67,工厂经过数据挑选挑选,使得Cmk大于1.67,挑选的精度数据在2%或3%以内的,通过计算Cmk才达到1.67的要求。
1.2原因分析
1.螺丝刀的精度不能满足当前Cmk的计算公式,精度的上下需要更换。
1.3解决方案
1.进行西格玛标准进行目前螺丝刀Cmk的公式进行正推,是否螺丝刀的Cmk能达到1.67。
2.在正态分布的模型中进行抽样对目前Cmk的公式进行反推,螺丝刀的Cmk能发达到1,67。
2 西格玛标准的定义
2.1正态分布
若随机变量 X服从一个位置参数为μ、尺度参数为σ的概率分布,且其概率密度函数为
则这个随机变量就称为正态随机变量,正态随机变量服从的分布就称为正态分布,记作X~N(μ,),读作X服从N(μ,),或X服从正态分布。
2.2标准正态分布
当μ=0,σ=1时,正态分布就成为标准正态分布
如图:
2.3正态函数的面积分布与西格玛的关系
正态函数的不定积分是一个非初等函数,称为误差函数
x(μ-σ,μ+σ),表示在一个西格玛的概率为0.682689492137,690,000失误/百万机会。
x(μ-2σ,μ+2σ),表示在两个西格玛的概率为0.954499736104,308,000失误/百万机会。
x(μ-3σ,μ+3σ),表示在三个西格玛的概率为0.997300203937,66,800失误/百万机会。
x(μ-4σ,μ+4σ),表示在四个西格玛的概率为0.999936657516,6,210失误/百万机会。
x(μ-5σ,μ+5σ),表示在五个西格玛的概率为0.999999426697,230失误/百万机会。
x(μ-6σ,μ+6σ),表示在六个西格玛的概率为0.999999998027,3.4失误/百万机会。
3 Cmk与Cpk的定义与关系
3.1Cpk与Cmk的定义
在说明Cmk计算方法之前,先阐述Cpk(potentialprocess capability index,潜在的工序能力指数)和Cpk(process capability index工序能力指数)计算方法。工序是产品制造的基本环节,若在生产过程中每一道工序的加工质量都比较高,则产品的质量定能够得到保证。产品或者服务的质量是可以用规格来衡量的,在规格范围内就认为是合格的,否则就认为不合格。过程能力指数的计算就是评价和衡量过程能力的重要环节和规格,甚至成为唯一的尺度[1]。
Cpk:工序能力指数,是指工序在一定时间里,处于控制状态(稳定状态)下的实际加工能力。它是工序固有的能力,或者说它是工序保证质量的能力。1.强调的是过程固有变差和实际固有的能力;2.分析前提是数据服从正态分布,且过程受控;3.至少1.33,过程稳定受控情况下适当频率抽25组至少100个样本
Cmk:表示仅由设备普通原因变差决定的能力,1.考虑短期离散,强调设备本身因素对质量的影响;2.用于新机验收时、新产品试制时、设备大修后等情况;3至少1.67;一般在机器生产稳定后约一小时内抽样10组50样本[2]。
3.2Cpk与Cmk的关系
Cmk与Cpk不同在于取样方法不同,是在机器稳定工作时至少连续50件的数据,Cmk=T/6西格玛,西格玛即可用至少连续50件的数据s估计,又可用至少连续50件的数据分组后的Rbar/d2来估计,由于根据美国工业界的经验,过程变差的75%来自设备变差,如果用至少连续50件的数据s估计的西格玛或用至少连续50件的数据分组后的Rbar/d2估计的西格玛来计算Cpk的话,人机料法环总普通原因变差为8西格玛, Cpk=T/8西格玛.当通过理想化模型,取样数量足够时,Cpk和Cmk接近。
4用正态分布进行Cmk和Cpk的推导过程
4.1Cmk的计算公式
S:取样数据的标准差,用STDEV公式直接计算
T:公差范围,即上、下极限值之差
K:为修正系数或偏离系数
Bi:平均值Xbar和测量的理论中间值之差
Bi=[Xbar-图纸中间值-(上偏差+下偏差)/2]
4.2Cpk的计算公式
USL:图纸上限尺寸,(中间值+上公差)
LSL:图纸下限尺寸,(中间值+下公差)
Xbar:每组抽样数据的平均数,然后再平均数(其实就是所有抽样数据的平均数)
Rbar:每组抽样数据的极差的平均数
d2:跟据抽样数据的多少而对应的修正系数,有表可查
4.3PPK的计算公式
S:取样数据的标准差,用STDEV公式直接计算
附注:Cmk和PPK的公式其实是一样的。西格玛和σ是同一意思。
4.4Cmk和Cpk在正态分布中的计算
由于处于积分状态,样点取数接近无穷个。在此状态下,样品标准差≈整体标准差可得:
一个西格玛标准时,Cpk=0.333333333333。
两个西格玛标准时,Cpk=0.666666666667。
三个西格玛标准时,Cpk=1。
四个西格玛标准时,Cpk=1.333333333333。
五个西格玛标准时,Cpk=1.666666666667。
六个西格玛标准时,Cpk=2。
5按照螺丝刀3σ±5%的精度进行整体分布进行100个抽样。
5.1理想情况下样本抽样表
个数 在正态分布中的扭力抽样符合螺丝的±5%+3σ的标准
1 0.523333
1 0.480833333
1 0.518333
1 0.4825
1 0.516667
1 0.484166667
1 0.515
2 0.485833333 0.514167
2 0.486666667 0.513333
2 0.4875 0.5125
3 0.488333333 0.511667 0.488333333
3 0.489166667 0.510833 0.510833333
4 0.49 0.51 0.49 0.51
4 0.490833333 0.509167 0.490833333 0.509167
5 0.491666667 0.508333 0.491666667 0.508333 0.491667
5 0.4925 0.5075 0.4925 0.5075 0.5075
5 0.493333333 0.506667 0.493333333 0.506667 0.493333
6 0.494166667 0.505833 0.494166667 0.505833 0.494167 0.505833
6 0.495 0.505 0.495 0.505 0.495 0.505
7 0.495833333 0.504167 0.495833333 0.504167 0.495833 0.504167 0.495833
7 0.496666667 0.503333 0.496666667 0.503333 0.496667 0.503333 0.496667
8 0.4975 0.5025 0.4975 0.5025 0.4975 0.5025 0.4975 0.4975
8 0.498333333 0.501667 0.498333333 0.501667 0.498333 0.501667 0.498333 0.501667
8 0.499166667 0.500833 0.499166667 0.500833 0.499167 0.500833 0.499167 0.500833
8 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5
5.2 Cpk和Cmk计算
目标扭力 0.5 上限% 5 下限% 5
上限扭力 0.525 下限扭力 0.475
平均值 0.5
方差 0.00006355555556
整体标准差 0.007972174
样本标准差 0.008012336
Cmk 1.040062868
由图表可知,当扭力上下限为5%时候,螺丝无法满足Cmk=1.67的要求。
5.3 按照螺丝刀在5σ的时候进行扭力精度调整
将上下限3σ±5%延伸至5σ±8.3%。
最大扭力 0.5 上限% 8.3 下限% 8.3
目标扭力 0.5 上限扭力 0.5415 下限扭力 0.4585
平均值 0.5
方差 0.00006355555556
整体标准差 0.007972174
样本标准差 0.008012336
Cmk 1.726504361
如表格所示,螺丝刀可以满足Cmk≥1.67。
根据调试的情况不同,可以存在一定量的样本中,Cmk可以大于Cpk的情况与理想状态分离,但是正常情况下,Cmk>1.67的时候需要Cpk>1.33。
6总结
目前螺丝刀的精度标为3西格玛±5%的精度时和以下精度一致。
螺丝刀的精度可以标定为±1.67%的精度满足1西格玛标准,此时此时Cpk≈0.33;
螺丝刀的精度可以标定为±3.33%的精度满足2西格玛标准,此时此时Cpk≈0.67;
螺丝刀的精度可以标定为±5%的精度满足3西格玛标准,此时此时Cpk≈1;
螺丝刀的精度可以标定为±6.67%的精度满足4西格玛标准,此时此时Cpk≈1.33;
螺丝刀的精度可以标定为±8.33%的精度满足5西格玛标准,此时此时Cpk≈1.67;
螺丝刀的精度可以标定为±10%的精度满足6西格玛标准,此时此时Cpk≈2;
螺丝刀的Cmk≥1.67需要在螺丝刀4西格玛的精度标准,及Cpk≥1.33的基础上才可以调整达到要求。当设备处于非优秀调试状态下,想要让Cmk≥1.67时候,需要在螺丝刀满足5西格玛的精度标准,Cpk≥1.67的情况下才能完成。
参考文献:
[1]罗孟然,丛明,顾齐芳,李泳耀,李宏坤.基于C_(mk)分析的加工中心精度稳定性评估[J].组合机床与自动化加工技术,2015(03):149-153.DOI:10.13462/j.cnki.mmtamt.2015.03.041.
[2]石枫.能力指数Ppk、Cpk、Cmk在实际工作中应用的探讨[J].电子测试,2014(20):29-31.
[3]赖涌丹.精益六西格玛在在线检测设备测量精度分析中的应用研究[J].机电工程技术,2021,50(02):186-189+223.
补充说明:可以以此为例进行其他设备的精度标准的推测和检测依据。
黄飞鸿
(宁波安德路工业自动化设备有限公司)
摘要:
随着日益规范化的设备使用过载中,对精度的标注更加规范化,以西格玛和精度范围作为精度的标准,从而衍生出满足精度标准的Cmk和Cpk的规律和计算方式的推算。以下内容以深圳艾而特工业自动化设备有限公司的ACT型螺丝刀作为范例进行演示。
关键词:精度;Cmk;Cpk;西格玛;
1 总结性描述
1.1背景
1.目前螺丝刀的进度在3西格玛±5%的精度情况下,在手持螺丝刀时候,扭力的测试数据很难计算Cmk1.67,工厂经过数据挑选挑选,使得Cmk大于1.67,挑选的精度数据在2%或3%以内的,通过计算Cmk才达到1.67的要求。
1.2原因分析
1.螺丝刀的精度不能满足当前Cmk的计算公式,精度的上下需要更换。
1.3解决方案
1.进行西格玛标准进行目前螺丝刀Cmk的公式进行正推,是否螺丝刀的Cmk能达到1.67。
2.在正态分布的模型中进行抽样对目前Cmk的公式进行反推,螺丝刀的Cmk能发达到1,67。
2 西格玛标准的定义
2.1正态分布
若随机变量 X服从一个位置参数为μ、尺度参数为σ的概率分布,且其概率密度函数为
则这个随机变量就称为正态随机变量,正态随机变量服从的分布就称为正态分布,记作X~N(μ,),读作X服从N(μ,),或X服从正态分布。
2.2标准正态分布
当μ=0,σ=1时,正态分布就成为标准正态分布
如图:
2.3正态函数的面积分布与西格玛的关系
正态函数的不定积分是一个非初等函数,称为误差函数
x(μ-σ,μ+σ),表示在一个西格玛的概率为0.682689492137,690,000失误/百万机会。
x(μ-2σ,μ+2σ),表示在两个西格玛的概率为0.954499736104,308,000失误/百万机会。
x(μ-3σ,μ+3σ),表示在三个西格玛的概率为0.997300203937,66,800失误/百万机会。
x(μ-4σ,μ+4σ),表示在四个西格玛的概率为0.999936657516,6,210失误/百万机会。
x(μ-5σ,μ+5σ),表示在五个西格玛的概率为0.999999426697,230失误/百万机会。
x(μ-6σ,μ+6σ),表示在六个西格玛的概率为0.999999998027,3.4失误/百万机会。
3 Cmk与Cpk的定义与关系
3.1Cpk与Cmk的定义
在说明Cmk计算方法之前,先阐述Cpk(potentialprocess capability index,潜在的工序能力指数)和Cpk(process capability index工序能力指数)计算方法。工序是产品制造的基本环节,若在生产过程中每一道工序的加工质量都比较高,则产品的质量定能够得到保证。产品或者服务的质量是可以用规格来衡量的,在规格范围内就认为是合格的,否则就认为不合格。过程能力指数的计算就是评价和衡量过程能力的重要环节和规格,甚至成为唯一的尺度[1]。
Cpk:工序能力指数,是指工序在一定时间里,处于控制状态(稳定状态)下的实际加工能力。它是工序固有的能力,或者说它是工序保证质量的能力。1.强调的是过程固有变差和实际固有的能力;2.分析前提是数据服从正态分布,且过程受控;3.至少1.33,过程稳定受控情况下适当频率抽25组至少100个样本
Cmk:表示仅由设备普通原因变差决定的能力,1.考虑短期离散,强调设备本身因素对质量的影响;2.用于新机验收时、新产品试制时、设备大修后等情况;3至少1.67;一般在机器生产稳定后约一小时内抽样10组50样本[2]。
3.2Cpk与Cmk的关系
Cmk与Cpk不同在于取样方法不同,是在机器稳定工作时至少连续50件的数据,Cmk=T/6西格玛,西格玛即可用至少连续50件的数据s估计,又可用至少连续50件的数据分组后的Rbar/d2来估计,由于根据美国工业界的经验,过程变差的75%来自设备变差,如果用至少连续50件的数据s估计的西格玛或用至少连续50件的数据分组后的Rbar/d2估计的西格玛来计算Cpk的话,人机料法环总普通原因变差为8西格玛, Cpk=T/8西格玛.当通过理想化模型,取样数量足够时,Cpk和Cmk接近。
4用正态分布进行Cmk和Cpk的推导过程
4.1Cmk的计算公式
S:取样数据的标准差,用STDEV公式直接计算
T:公差范围,即上、下极限值之差
K:为修正系数或偏离系数
Bi:平均值Xbar和测量的理论中间值之差
Bi=[Xbar-图纸中间值-(上偏差+下偏差)/2]
4.2Cpk的计算公式
USL:图纸上限尺寸,(中间值+上公差)
LSL:图纸下限尺寸,(中间值+下公差)
Xbar:每组抽样数据的平均数,然后再平均数(其实就是所有抽样数据的平均数)
Rbar:每组抽样数据的极差的平均数
d2:跟据抽样数据的多少而对应的修正系数,有表可查
4.3PPK的计算公式
S:取样数据的标准差,用STDEV公式直接计算
附注:Cmk和PPK的公式其实是一样的。西格玛和σ是同一意思。
4.4Cmk和Cpk在正态分布中的计算
由于处于积分状态,样点取数接近无穷个。在此状态下,样品标准差≈整体标准差可得:
一个西格玛标准时,Cpk=0.333333333333。
两个西格玛标准时,Cpk=0.666666666667。
三个西格玛标准时,Cpk=1。
四个西格玛标准时,Cpk=1.333333333333。
五个西格玛标准时,Cpk=1.666666666667。
六个西格玛标准时,Cpk=2。
5按照螺丝刀3σ±5%的精度进行整体分布进行100个抽样。
5.1理想情况下样本抽样表
个数 在正态分布中的扭力抽样符合螺丝的±5%+3σ的标准
1 0.523333
1 0.480833333
1 0.518333
1 0.4825
1 0.516667
1 0.484166667
1 0.515
2 0.485833333 0.514167
2 0.486666667 0.513333
2 0.4875 0.5125
3 0.488333333 0.511667 0.488333333
3 0.489166667 0.510833 0.510833333
4 0.49 0.51 0.49 0.51
4 0.490833333 0.509167 0.490833333 0.509167
5 0.491666667 0.508333 0.491666667 0.508333 0.491667
5 0.4925 0.5075 0.4925 0.5075 0.5075
5 0.493333333 0.506667 0.493333333 0.506667 0.493333
6 0.494166667 0.505833 0.494166667 0.505833 0.494167 0.505833
6 0.495 0.505 0.495 0.505 0.495 0.505
7 0.495833333 0.504167 0.495833333 0.504167 0.495833 0.504167 0.495833
7 0.496666667 0.503333 0.496666667 0.503333 0.496667 0.503333 0.496667
8 0.4975 0.5025 0.4975 0.5025 0.4975 0.5025 0.4975 0.4975
8 0.498333333 0.501667 0.498333333 0.501667 0.498333 0.501667 0.498333 0.501667
8 0.499166667 0.500833 0.499166667 0.500833 0.499167 0.500833 0.499167 0.500833
8 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5
5.2 Cpk和Cmk计算
目标扭力 0.5 上限% 5 下限% 5
上限扭力 0.525 下限扭力 0.475
平均值 0.5
方差 0.00006355555556
整体标准差 0.007972174
样本标准差 0.008012336
Cmk 1.040062868
由图表可知,当扭力上下限为5%时候,螺丝无法满足Cmk=1.67的要求。
5.3 按照螺丝刀在5σ的时候进行扭力精度调整
将上下限3σ±5%延伸至5σ±8.3%。
最大扭力 0.5 上限% 8.3 下限% 8.3
目标扭力 0.5 上限扭力 0.5415 下限扭力 0.4585
平均值 0.5
方差 0.00006355555556
整体标准差 0.007972174
样本标准差 0.008012336
Cmk 1.726504361
如表格所示,螺丝刀可以满足Cmk≥1.67。
根据调试的情况不同,可以存在一定量的样本中,Cmk可以大于Cpk的情况与理想状态分离,但是正常情况下,Cmk>1.67的时候需要Cpk>1.33。
6总结
目前螺丝刀的精度标为3西格玛±5%的精度时和以下精度一致。
螺丝刀的精度可以标定为±1.67%的精度满足1西格玛标准,此时此时Cpk≈0.33;
螺丝刀的精度可以标定为±3.33%的精度满足2西格玛标准,此时此时Cpk≈0.67;
螺丝刀的精度可以标定为±5%的精度满足3西格玛标准,此时此时Cpk≈1;
螺丝刀的精度可以标定为±6.67%的精度满足4西格玛标准,此时此时Cpk≈1.33;
螺丝刀的精度可以标定为±8.33%的精度满足5西格玛标准,此时此时Cpk≈1.67;
螺丝刀的精度可以标定为±10%的精度满足6西格玛标准,此时此时Cpk≈2;
螺丝刀的Cmk≥1.67需要在螺丝刀4西格玛的精度标准,及Cpk≥1.33的基础上才可以调整达到要求。当设备处于非优秀调试状态下,想要让Cmk≥1.67时候,需要在螺丝刀满足5西格玛的精度标准,Cpk≥1.67的情况下才能完成。
参考文献:
[1]罗孟然,丛明,顾齐芳,李泳耀,李宏坤.基于C_(mk)分析的加工中心精度稳定性评估[J].组合机床与自动化加工技术,2015(03):149-153.DOI:10.13462/j.cnki.mmtamt.2015.03.041.
[2]石枫.能力指数Ppk、Cpk、Cmk在实际工作中应用的探讨[J].电子测试,2014(20):29-31.
[3]赖涌丹.精益六西格玛在在线检测设备测量精度分析中的应用研究[J].机电工程技术,2021,50(02):186-189+223.
补充说明:可以以此为例进行其他设备的精度标准的推测和检测依据。
 TA的首页
TA的首页
![VU]X7PSX1L7DETJ__5SVAO.png VU]X7PSX1L7DETJ__5SVAO.png](https://www.6sq.net/uploads/article/20220920/2a9650149094b22d2a6f27c57af2f326.png)

![S]8@_PQN_{_0R8}K6U8K@7.png S]8@_PQN_{_0R8}K6U8K@7.png](https://www.6sq.net/uploads/article/20220920/3e0606b2c3abaf89aab4c2404e0144a3.png)