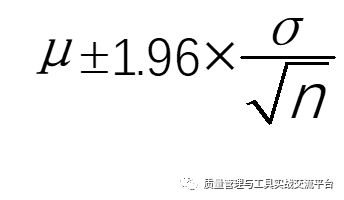控制图出现失控后一定要隔离产品和停线吗？

在我的前面的控制图相关文章中，讨论了控制图为什么能够发现失控的、子组大小的确定方法、判异与判稳的准则及其选择的依据等，而在控制图的实操过程中，还有一个避不开的问题，这就是：当发现失控时要对过程进行原因调查，那么还要必须隔离产品或者停线吗？

这是一个比较尖锐的问题，因为这关系到产品交付的及时性，会对相关部门的利益产生影响，尽管我们都是为了公司和客户着想。

是否需要隔离产品或者停线，取决于我们使用并出现下列判异准则中的哪几个：


准则1：1个点，距离中心线大于3个标准差

准则2：连续9个点，在中心线同一侧

准则3：连续6个点，全部递增或全部递减

准则4：连续14个点，上下交错

准则5：3个点中有2个点，距离中心线（同侧）大于2个标准差

准则6：5个点中有4个点，距离中心线（同侧）大于1个标准差

准则7：连线15个点，距离中心线（任一侧）1个标准差以内准则8：连线8个点，距离中心线（任一侧）大于1个标准差判异准则1是必须使用的，我们就先讨论准则1。

均值点出界，又可分为两种情形：

情形1——均值点超出控制限，且超过规格限，是必须停线和隔离产品的，这是毫无疑问的，因为已经产生了不合格了，即使是过程特性，也意味着对应的产品特性大概率出现不合格。这种情形，我们就不进一步展开讨论了。

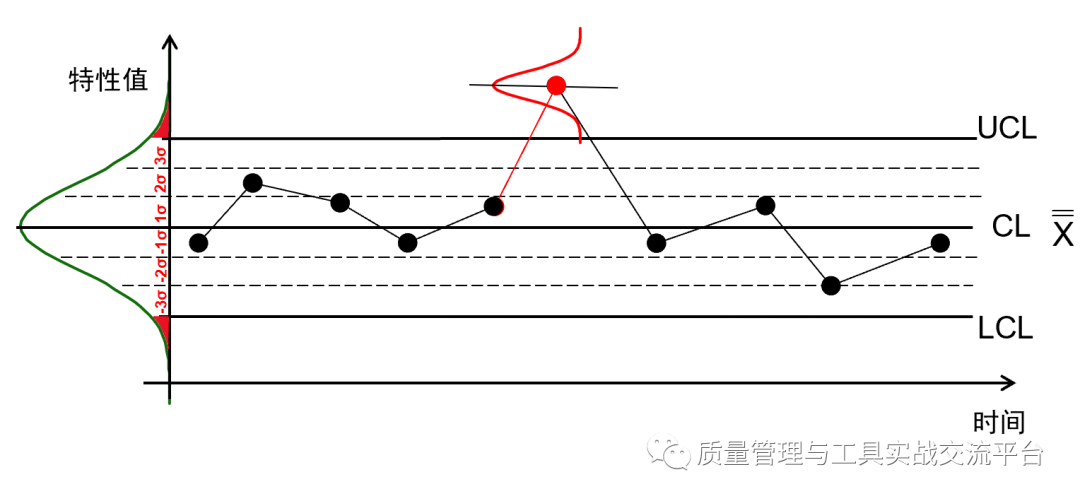
情形2——均值点超出控制限，但未超规格限。要知道未超规格限，只是我们所抽取的子组的均值未超规格限，这里面又可分为两种情况：子组内有个别单值可能会超规格限，这个容易确认，在测量样本时就知道了；另一种情况是在这个抽样时间段内，未抽到的产品特性可能还会有超规格，那么，如果有，会有多大的概率存在不合格呢？我们还是以最常用的均值-极差图为例。在均值图上出现了超界点，实际上就是均值发生了显著的偏移，不管是一种暂时性的偏移，还是永久性的。因为控制图的点是抽样所得，这个点就代表着抽样间隔内所生产的所有产品的特性值构成了一个新的分布，如下图所示，只是这个新的分布的均值与之前稳定时的分布均值有了显著的变异。



那么，我们现在来使用95%置信区间来估计超界均值点所代表的抽样时间间隔内的这个小的“总体均值”（后面叫做“抽样间隔总体”）是多少。

下面先简要介绍置信区间的概念。

由于不是100%检验，我们使用样本均值来对总体进行“点估计”，根据“中心极限定理”可知，样本均值等于总体的均值。但是由于总体均值是通过样本来估计的，所以总是存在抽样误差，这个误差就是：



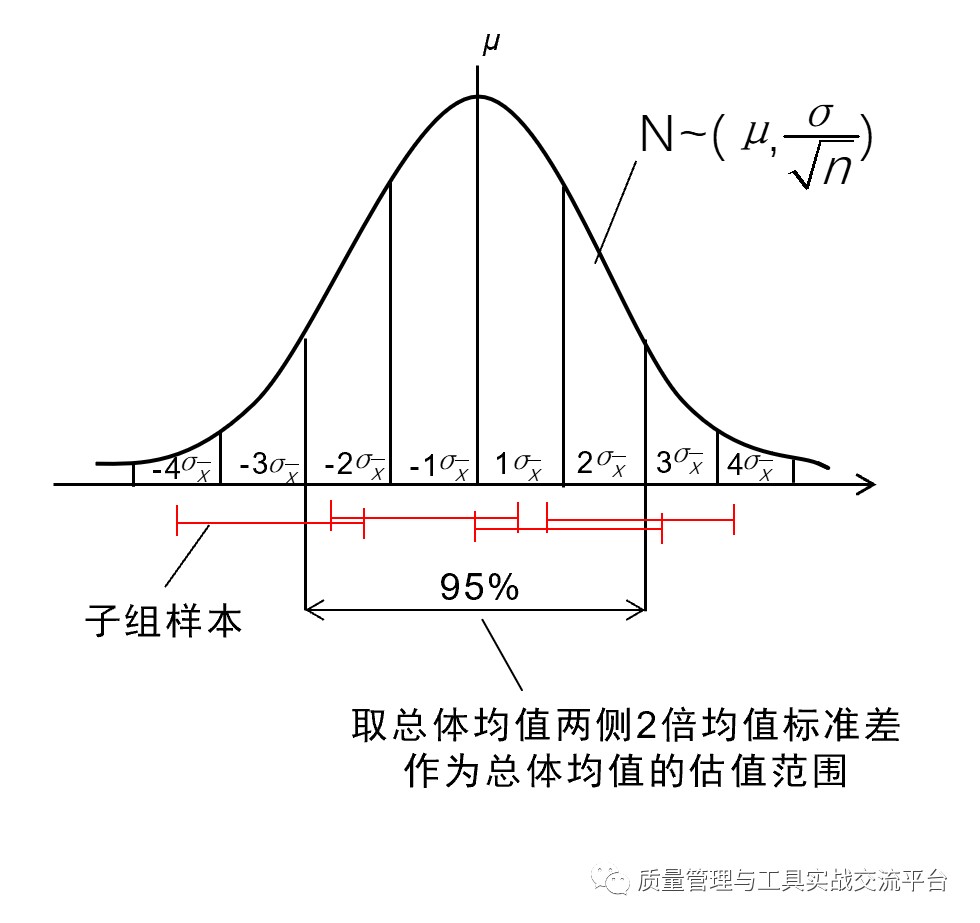
其中，σ 在本案例中是抽样时间段内特性单值的标准差，n 是每次抽样的数量。用子组样本均值估计抽样间隔总体均值存在上述抽样误差，同时这个抽样误差也是由（子组）样本均值所构成的正态分布的标准差，我们也把它叫做“标准误”。这个由均值点构成的正态分布的均值，就是我们要估计的“抽样间隔总体均值 μ”，如下图所示：



那么，我们就取正态布总体均值两侧2倍均值标准差，作为抽样间隔总体均值的估值范围，如上图所示，可见，这个范围正好占正态分布的95%，我们用下列95%置信区间公式来表达：



式中，μ 为样本均值，σ 为样本单值的标准差，n 为子组的大小，即抽样数量。

下一步，我们就看看特性的规格限是否落在了上述置信区间内，如果是，我们就可以说：抽样时间段内，有95%的可能性出现了不合格。

因此，准则1失控了，我们需要通过上述具体的计算，来评估产品的风险高低，做出是否隔离产品的决策，一旦隔离，就应进行全检。另外，判异准则1失控了，通常是需要停线来找原因的。

当需要隔离产品时，不能直接隔离一个最近一个抽样间隔的产品，还要根据具体的失控ARL来推算出实际失控的时间点在哪里，具体的原理，请详见我的另一篇文章“一个均值-极差控图子组大小的问题”，里面有详尽的介绍，就不在本文中赘述了。

准则5、6也属于均值偏移类型的失控，因此，是否隔离产品，也应通过上述的计算来做决策。

除了准则1、5、6以外，其他的准则，则属于趋势和点链了，出现不合格的可能性不大，只是调查原因即可。

下面我们再来讨论一下在极差图上出现超界点的问题。

极差图上出现超出下控制限的点，是子组的极差变小了，由此估计的产品的特性的标准差也就是离散度变小，这是我们所期望的，这往往是改善的结果。当极差图上出现超出上控制限的点时，就说明了子组样本特性的极差变大了，对应的产品特性间的标准差变大了，这就影响到了过程性能指数变大了，过程性能指数见下列公式：[图片]





我们需要从失控时开始，计算一下失控后具体过程的性能指数PPK，如果不能满足目标值，则应将产品隔离，进行全检。