选择实验设计中的最优设计
我们知道,DOE在质量控制的整个过程中扮演了非常重要的角色,它是我们产品质量提高,工艺流程改善的重要保证。但基于实验环境和实验成本等因素考虑,有时,我们并不能够实现所有的因子水平组合。这样我们就需要根据实际场景执行最优设计。
最优设计,是指在给定因子空间内试验单元数相等的所有试验方案中,各回归系数的广义方差最小的试验方案。最优设计是在因子空间中可能产生的试验方案中信息矩阵行列式值最大,也是相关矩阵行列式值最小的试验方案。最优设计的出发点是优化回归方程的统计性质。最优设计试验方案通常用数值方法构造,先给定一个初始方案,然后用计算机构造出一系列方案的信息矩阵行列式值逐渐增大,并收敛于最优设计方案。最优设计有一次模型和二次模型的区别,也有饱和的与非饱和的区别。Minitab 的最优设计功能可以与一般全因子设计、响应曲面设计以及混料设计一起使用。
【例】工艺工程师希望建立将导致生物膜厚度及最大拉力的时间和温度设置。 由于这两个因素,她必须小心处理薄膜,因为如果过程运行太冷/太短,薄膜不会固化,如果运行太热/时间太长,薄膜会燃烧。 具体来说,为了让薄膜固化但不燃烧,她有以下限制:
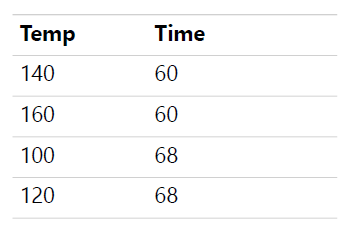
(1)在最短的 60 分钟的循环时间内,它们必须在至少 140 度但不超过 160 度的温度下运行;
(2)在最长的 68 分钟的循环时间内,它们必须在至少 100 度但不超过 120 度的温度下运行。
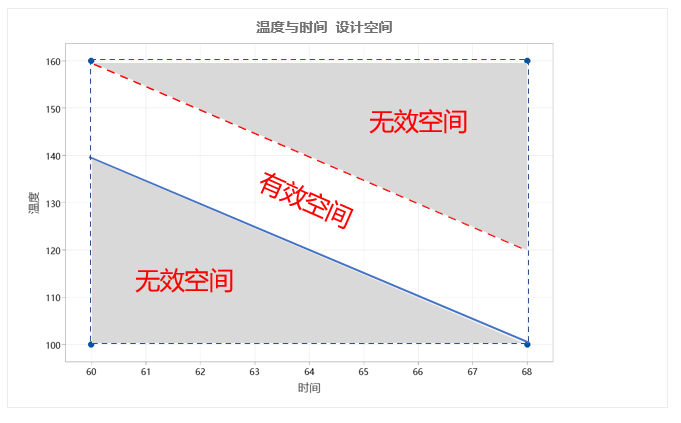
根据这样的要求,就相当于我们执行2因子2水平设计,但是实验区域受限(如下图)
我们可以根据线性回归特性,将边界线的模型表达出来:
Temp=460-5*Time
Temp=440-%*Time
为了得到实验空间,我们借助Minitab软件的产生网格数据,初步得到实验的空间:
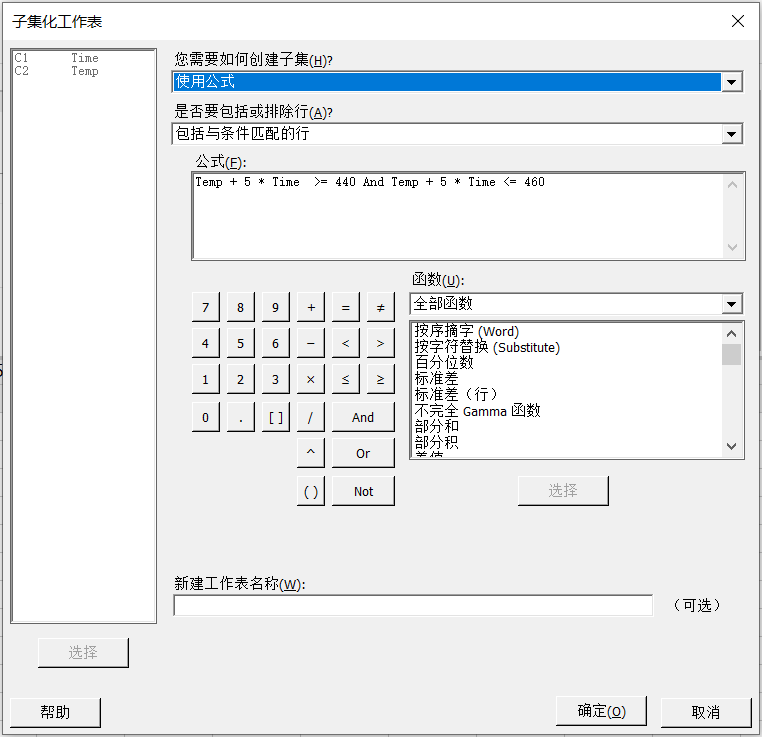
从备选点集中选择设计点以得到最优设计。当原始设计包含的点比限于时间或财力所能实现的多时,通常使用选择最优设计来减少试验数。虽然这些数据点可能是将来的试验点,但根据前面的介绍,有些空间数据并没有实际意义,因此我们需要截取相应的实验点,这个工作可以通过Minitab的子集化工作表实现:
根据子集化工作表的设置,将实验空间进一步优化,如下图所示:
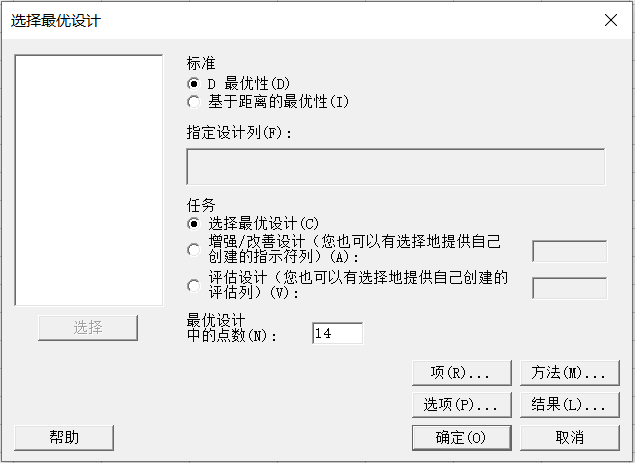
这些实验组内次数非常庞大,基于实验的原则,我们不可能将所有组合全部实施,接下来,利用Minitab的“选择最优设计”可以帮我们快速选择:
这样一来,Minitab就可以从候选设计组合中选择最优的14次运行,基于这些实验结果,Minitab可以拟合出二次回归模型。D 最优性将拟合模型中回归系数的方差降到最低,从而提供最精确的效应估计。
指定模型后,Minitab 将从一组候选设计点中选择满足D 最优标准的设计点。
最优设计,是指在给定因子空间内试验单元数相等的所有试验方案中,各回归系数的广义方差最小的试验方案。最优设计是在因子空间中可能产生的试验方案中信息矩阵行列式值最大,也是相关矩阵行列式值最小的试验方案。最优设计的出发点是优化回归方程的统计性质。最优设计试验方案通常用数值方法构造,先给定一个初始方案,然后用计算机构造出一系列方案的信息矩阵行列式值逐渐增大,并收敛于最优设计方案。最优设计有一次模型和二次模型的区别,也有饱和的与非饱和的区别。Minitab 的最优设计功能可以与一般全因子设计、响应曲面设计以及混料设计一起使用。
【例】工艺工程师希望建立将导致生物膜厚度及最大拉力的时间和温度设置。 由于这两个因素,她必须小心处理薄膜,因为如果过程运行太冷/太短,薄膜不会固化,如果运行太热/时间太长,薄膜会燃烧。 具体来说,为了让薄膜固化但不燃烧,她有以下限制:
(1)在最短的 60 分钟的循环时间内,它们必须在至少 140 度但不超过 160 度的温度下运行;
(2)在最长的 68 分钟的循环时间内,它们必须在至少 100 度但不超过 120 度的温度下运行。
根据这样的要求,就相当于我们执行2因子2水平设计,但是实验区域受限(如下图)
我们可以根据线性回归特性,将边界线的模型表达出来:
Temp=460-5*Time
Temp=440-%*Time
为了得到实验空间,我们借助Minitab软件的产生网格数据,初步得到实验的空间:
从备选点集中选择设计点以得到最优设计。当原始设计包含的点比限于时间或财力所能实现的多时,通常使用选择最优设计来减少试验数。虽然这些数据点可能是将来的试验点,但根据前面的介绍,有些空间数据并没有实际意义,因此我们需要截取相应的实验点,这个工作可以通过Minitab的子集化工作表实现:
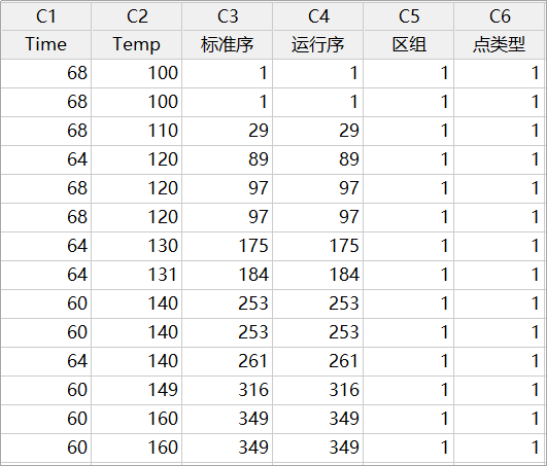
根据子集化工作表的设置,将实验空间进一步优化,如下图所示:
这些实验组内次数非常庞大,基于实验的原则,我们不可能将所有组合全部实施,接下来,利用Minitab的“选择最优设计”可以帮我们快速选择:
这样一来,Minitab就可以从候选设计组合中选择最优的14次运行,基于这些实验结果,Minitab可以拟合出二次回归模型。D 最优性将拟合模型中回归系数的方差降到最低,从而提供最精确的效应估计。
指定模型后,Minitab 将从一组候选设计点中选择满足D 最优标准的设计点。
 TA的首页
TA的首页