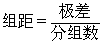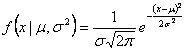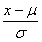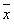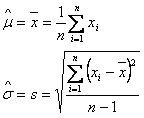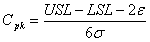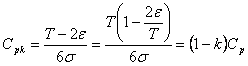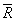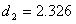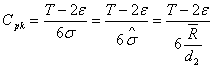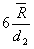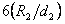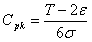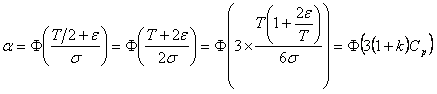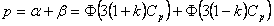过程能力分析的来龙去脉
过程能力分析离不开正态分布的知识,所以我们先从直方图及正态分布讲起。
一、直方图与正态分布
描绘计量型数据的分布离不开直方图,下面先来回顾一下直方图的画法:
1、确定所要研究的对象,为了能更准确的反映总体的状况,至少收集100个数据。
2、计算数据的极差,极差=最大值-最小值。
3、确定分组数,一般来说可以按k=1+3.32lg(n)来定分组数,其中,n为样本量。
4、计算组距,
5、确定组界,组界由下组界和上组界构成。第一组的下组界为最小值-最小分度值的一半,第一组的上组界为第一组的下组界+组距,以此类推。
6、统计数据落入每组中的频数。
7、以组距为底,频数为高画直方,就可以得到一张直方图。
下面举一个画直方图的例子:
您在一家汽车工厂工作,目前正面临所用凸轮轴长度的变异性问题。您想了解由两家供应商提供的凸轮轴的质量是否相当,因此从每家随机抽取 100 件凸轮轴测量其长度。请分别给这两家供应商的数据画两张直方图。
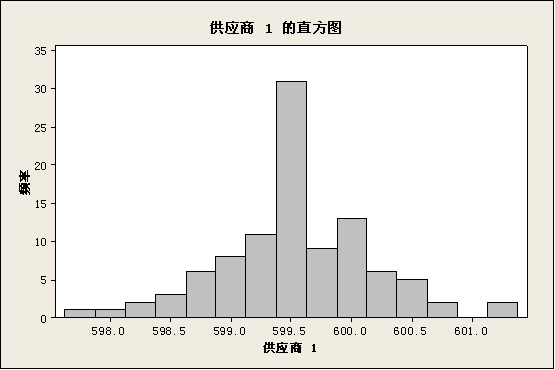
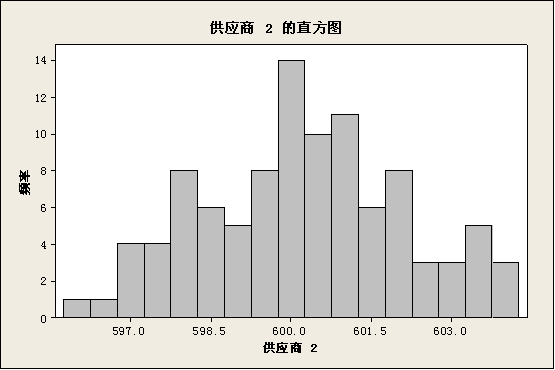
手工画直方图比较繁琐,我们可以利用数据统计分析软件——Minitab来画直方图,画出的直方图如下:
从上面两张图可以发现:供应商1提供的凸轮轴的长度数据比供应商2的更加集中一点,表现为中间多两头少,而供应商2的数据就比较分散,凭直觉判断,我们应该选用供应商1的凸轮轴。
直方图有频数直方图和频率直方图,上面我们介绍的就是频数直方图。如果在画直方图时把频数替换为频率就成了频率直方图。频率是频数除以样本量,所以频率直方图就是频数直方图在坐标轴缩小“样本量”倍,但从形状上来看与频数直方图是一模一样的。
下面我们要在频率直方图的基础上来了解一下分布的概念。如果在画频率直方图时我们限定两个条件①收集的数据足够多;②分组数为无穷多组,大家想一想,这样画出来的直方图将会变成什么形状?
(直方图上的每个直方将会变成一条线)
每一条线的高度在数学上称为“概率密度”,如果用一条光滑的曲线把这些线的端点连接起来,就是我们平时所讲的分布曲线。所以分布曲线并不是很难理解的东西的,它实际上是概率密度函数在图形上的反映。
数据的分布形状有很多种类型,我们平时接触到最多也是最常用的分布是正态分布。分布的形状跟数据的类型有关。不同类型的数据具有不同的分布。数据通常分为两类:连续型数据(或者叫做计量型数据)和离散型数据(或者叫做计数型数据)。所谓连续型数据就是数据之间的间隔是可以无限细分的,比如长度是可以无限细分的,米可以分成分米,厘米,毫米,微米,纳米,……,所以长度就是一个连续型数据,体积、时间、压力等都是连续型数据。离散型数据是指不能无限细分的,它总存在一个最小的数据间隔,比如,不合格品数,它只能以“整”个来描述,不可能说成1.5个不合格品,2.5个不合格品,象这样一类的数据就是离散型数据,离散型数据还有很多,比如外观缺陷数,瑕疵数等等。
我们平时接触到最多也是最常用的分布是正态分布。正态分布也称高斯分布,它是由德国数学家高斯于1809年正式给出表达式的。为了纪念高斯的伟大贡献,在德国10马克的钞票上不但印上了高斯的头像,而且把正态分布曲线连同它的表达式印在钞票的正面。
正态分布的数学表达式为:
这个数学表达式中竖线后面的两个字母是正态分布的两个分布参数。μ是正态分布的分布中心, σ2是正态分布的方差,σ就是正态分布的标准差。我们只要知道这两个参数,一条正态分布曲线就可以把它确定下来。任何一条正态分布曲线都可以形象地描述为“中间高、两边低、左右对称、延伸到无穷”的钟形曲线。
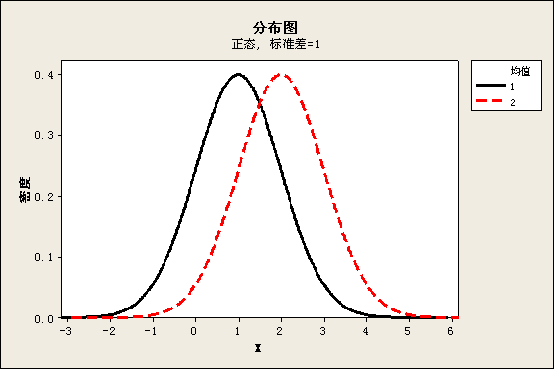
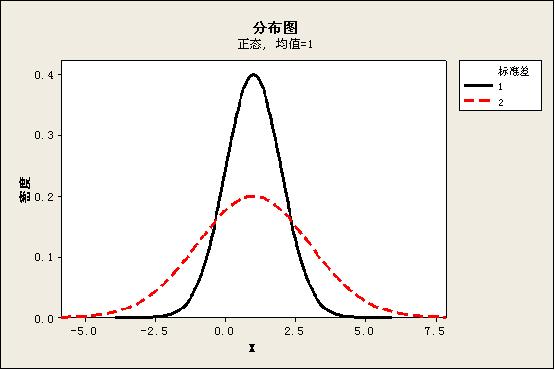
分布中心反映了正态分布在横轴上的位置,而标准差反映了正态分布的离散状况,以下是不同分布中心和标准差的正态分布的比较。
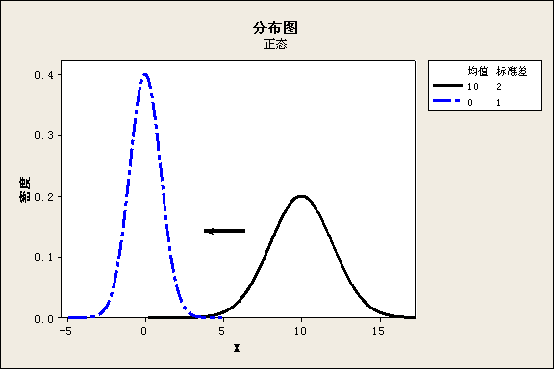
有一类正态分布我们必须熟练应用,那就是标准正态分布。所谓标准正态分布就是分布中心为0,标准差为1的正态分布,任何一个正态分布都可以通过 数学变换转换成标准正态分布。以下就是一个分布中心为10,标准差为2的正态分布转换前后的图形。
下面我们来说说如何来计算μ和σ。μ和σ在数理统计上有专门的定义,但如果按照定义去求μ和σ的精确值几乎不大可能。我们通常是利用样本的状况去推断总体的状况,这在统计学上就称为参数估计。比如对于正态分布的中心和标准差,我们就可以用样本均值 和样本标准差s来估计。为了使估计值和精确值有所区分,我们用 分别表示μ和σ的估计值。
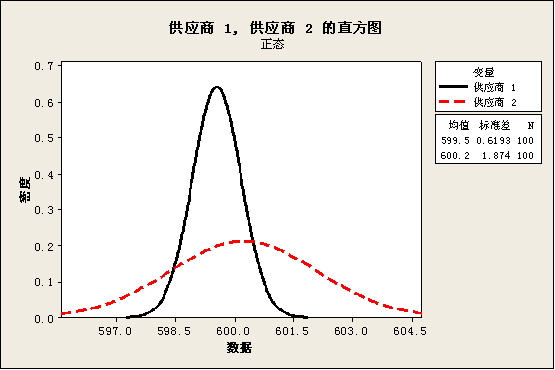
下面我们对上面提到的凸轮轴长度的数据再用正态分布曲线拟合一下,可以得到以下图形:
现在我们可以用数据来解释供应商1与供应商2之间的差异了:供应商 1 的凸轮轴似乎比供应商 2 的凸轮轴短。这可以从表格中的平均值(分别为 599.5 和 600.2)以及拟合正态分布峰值的相对位置看出来。
供应商 2 样本的标准差 (1.874) 远远高于供应商 1 的标准差 (0.6193)。这使得供应商 2 的拟合正态分布较低且较宽。供应商 2 的产品中大量变异性可能是导致凸轮轴长度不一致的主要原因。
二、过程输出与正态分布
过程输出 → 产品 → 产品可以用质量特性值来表示 → 质量特性值可分为计量型和计数型数据 → 数学理论上可以证明,如果某项计量型数据的指标受到很多项随机因素的干扰,而每项干扰都很小的话,则所有干扰影响的综合结果将导致此项指标的分布为正态分布
通过上面这段文字的指引,我们可以发现,如果过程的输出可以用计量型数据来表示的话,那么往往就可以用正态分布来表示过程的输出。正因为我们要了解过程的输出,而输出又可以用正态分布来表示,这就是我们为什么要学习正态分布的原因。
三、正态分布与过程不合格品率
也许生产控制人员最关心的问题就是产品的不合格品率。那么我们有没有办法通过正态分布来求产品的不合格品率呢?
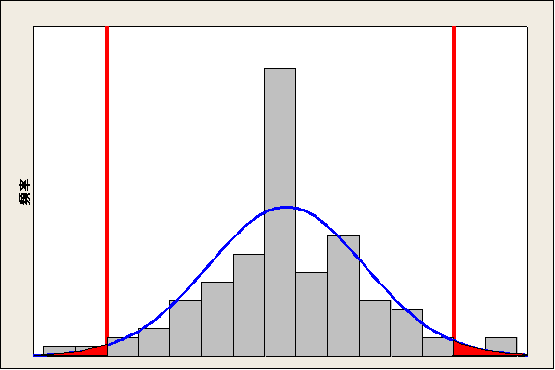
假如有一个磨加工车间在磨一只产品,它的规范限是9.8—10.2,通过抽取样本画出的频率直方图如下:
图上的两条红线就是产品的规范限,从图上标明的数据很容易可以知道,这个样本中的不合格品率是0.01+0.01+0.02=0.04,也就是把所有超过规范限的“直方”加起来。而通过前面所学的知识我们知道,频率直方图上的一个直方在正态分布曲线图上就是一条线,如果要通过正态分布曲线来求不合格品率,只需把超出规范限以外的所有的“线”加起来,而所有的线加起来就构成了“面积”。所以利用正态分布求不合格品率就变成了求超出规范限以外的正态分布曲线与横轴所围成的面积。
那么如何来求“超出规范限以外的正态分布曲线与横轴所围成的面积”呢?这个比较复杂,需要运用高等数学里的积分的方法求。但是我们可以借助MINITAB软件把它求出来。比如上面所举的例子,磨加工高度的规范限是9.8—10.2,现在通过抽取样本计算出均值为10.1,标准差为0.1,我们可以先通过正态分布求出该磨加工过程的合格品率。
通过上图可知,该磨加工过程的合格品率为84%,那么不合格品率就是16%。
假如通过改进过程,使得过程的平均值靠近公差带中心,即10,我们再来看一下过程的不合格品率会发生什么变化。
这时,过程的合格品率就提高到了95.4%,而不合格品率就降低为4.6%。
如果过程的均值没有发生变化,但设法提高了过程的加工精度,标准差由0.1减小为0.07,我们再来看一下过程的不合格品率又发生了什么变化。
我们可以发现合格品率由84%提高到了92.3%,而不合格品率降为7.7%。
最后我们得出减小过程不合格品率的两种策略:
在产品的公差范围不变的情况下,通过改进过程,使得过程的均值向公差带中心靠拢和/或减小过程的变差,可以显著地减小过程的不合格品率。
在两种策略中,相比较而言,让过程均值向公差带中心靠拢更容易实现一些。所以在过程不合格品率过大的情况下,首先要分析一下过程均值有没有跟公差带中心靠拢,然后再设法提高加工的精度。
四、过程能力指数
通过上面的介绍,我们知道,过程是可以用分布来描述的。而分布有它的一些特定的参数,比如分布中心和标准差。分布参数不同,满足顾客要求的能力也不同。比如标准差大的比标准差小的满足顾客要求的能力要差,因为标准差大的过程产生的不合格品会多一些。我们通常把6倍的标准差称为过程的能力。把过程能力与顾客的要求(即公差范围)去比较,称为过程能力指数。所以过程能力指数是表征过程满足顾客要求的能力的指标。
过程能力指数的计算公式是:
但是,如果标准差相同,分布中心不同,这两个过程满足顾客要求的能力也是不同的。如下图所示,两个过程标准差相同,但分布中心相差ε,这两个过程的不合格品率也是不同的。
如果光从Cp来表示还不能区分这两个过程满足顾客能力的大小,所以又增加了一个指数Cpk:
其中ε为过程分布中心偏离公差带中心的距离。
对Cpk的算式进行简单处理,可以得到如下等式:
令:T=USL-LSL
接下来的问题是,如何来估计总体的标准差σ?在解决这个问题之前,我们先要了解一下稳定的和不稳定的过程。
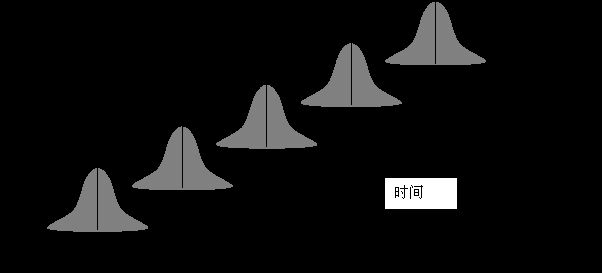
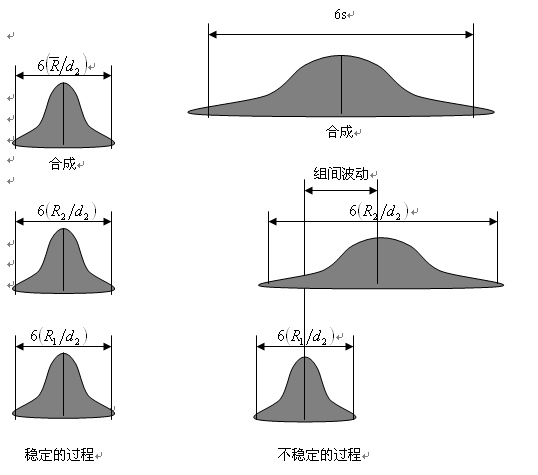
所谓稳定的过程是在任何一个时刻去观测过程,它的分布位置和分布宽度都是恒定不变的。如下图所示的就是一个稳定的过程。它的特点是过程的均值和标准差都保持不变。
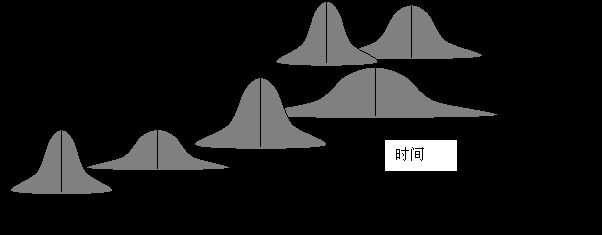
而不稳定的过程是指在不同的时刻去观测过程,它的分布位置和分布宽度都可能会发生变化。如下图所示的就是一个不稳定过程。
对于不稳定的过程,任一时刻的过程的输出的标准差都可能会不同,用任一时刻的过程输出的标准差来代表整个过程的标准差都是片面的,不合理的。因此计算过程能力指数有一个前提条件,那就是:过程必须预先用控制图来判断是稳定的。在这种状态下可以用 来估计σ,其中 是控制图当中的极差平均值, 是一个跟子组大小有关的系数,可查表。比如当子组大小为5的时候, 。
在这时候过程能力指数就可表示为:
可是如果过程确实是不稳定的怎么办?这时候我们可以用合并的标准差,也就是样本标准差s来估计总体的标准差。
当σ用s来估计时,得到的就不是过程能力指数,而是过程性能指数Ppk。
接下来我们来看看
和6s有什么区别。我们用图示的方法来说明。
对于稳定的过程,任一时刻的输出的中心和分布宽度基本上是不变的。如果把某一时刻的过程输出当成一个子组,那么每个子组之间只存在着组内波动, , ,……,表示的就是组内波动。它不存在着组与组之间的波动。而且组内的波动也是相等的,只是由于抽样的缘故,它们之间会存在略小的差别。总的过程波动可以用各个组内波动的平均 来估计。从波动引起的机理上来说,组内波动主要由偶然因素引起,组间波动由异常因素引起。所以稳定的过程也可以说是只有偶然因素在起作用的过程。而不稳定的过程是除了组内波动以外,还有组间波动,组间波动主要表现为子组的分布中心发生了漂移,而且从上图可以看出组内的波动也可能是不相等的。不稳定的过程是除了偶然因素在起作用以外还有异常因素在起作用的过程。所以总的过程标准差必须用合并的标准差,即样本标准差s来估计。这个s既包括了偶然因素引起的波动,又包括了异常因素引起的波动,最后计算出来的s应该比其中任何一个都要大。如果一个过程计算出的s与 差不多大,那么我们也可以大致推断过程是稳定的。
正因为 与6s存在上面这样的一种关系,所以从理论上来说过程性能指数Ppk总要比Cpk小。
因为在实际过程运行中,稳定是相对的,变化是绝对的。不发生变化(这种变化是由于异常因素在起作用而引起)的过程几乎是不可能,即便是稳定的过程,也只能是保持在相对来说比较长的一段时间内。所以我们有时把过程能力指数称为短期过程能力指数,把过程性能指数称为长期过程能力指数。
如果把一个过程比作一个人的话,那么一个稳定的过程就相当于是一个精神正常的人,而一个不稳定的过程就象是一个有精神病的人,我们谁都希望跟精神正常的人打交道,谁都不愿意跟精神不正常的人相处。因为我们对一个精神病人的行为是无法把握的,这就会增加我们心中的恐惧感。让过程处于稳定受控状态是现场控制人员的一项重要任务。上面我们也提到,过程总有一种由稳定向不稳定变化的趋势,怎么样发现过程已经开始发生变异是采取措施的关键。控制图就是帮助我们识别过程发生变异的重要工具。如果我们在控制图上规定一些采取措施的“行动点”,及时对开始变异的过程加以调整,我们是完全能够使过程处于稳定状态的。
下面举一个利用MINITAB进行过程能力分析的例子。
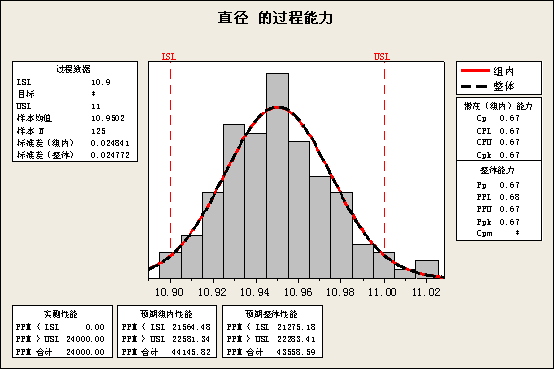
某台机器连续生产钢珠,直径是它的一个重要质量特性。为对钢珠直径进行控制,每隔15分钟抽样1次,每次抽取产品5个,共抽样25次。测量并记录数据。经检验钢珠直径服从正态分布,试绘制Xbar—R控制图并进行过程能力分析。
首先是利用MINITAB画出控制图,判断这个过程是否处于稳定状态。
丛图上可知,所有的点都在控制限内,并且也没有非随机的趋势,因此我们可以判断生产过程处于稳定状态。接下来我们进行过程能力的分析。
观察上图,可以获得很多信息。首先,图正中带两条拟合曲线的直方图给了我们最直观的认识。两条线几乎完全重合,将左上角的标准差(组内)=0.024841与标准差(总体)=0.024722相比,相差甚微,这说明除了组内的偶然因素引起的波动以外,几乎不存在组间波动。其次,Cp=0.67,Cpk=0.67,两者均小于1.33,说明过程能力不足,需要改进过程,两者没有差别,说明主要改进方向是设法降低过程的偶然因素引起的波动。再次,图左下方的PPM值的统计从可能出现的不良率这个角度解释了过程能力的优劣。
五、过程能力指数和不合格品率之间的关系
从过程能力指数的计算公式
可知,提高过程能力指数的途径有三种:
1、增大公差范围。
2、减少分布中心和公差带中心的偏移量。
3、减少过程输出的标准差。
在上面讲到不合格品率的内容时,我们也分析了减少不合格品率的途径。通过对比,我们发现减少不合格品率与提高过程能力指数的途径是一样的,这说明两者之间肯定存在着千丝万缕的联系。那么它们之间到底存在着什么样的精确关系呢?下面就为大家来解析这个问题。
上图中α为超出公差下限的不合格品率,β超出公差上限的不合格品率。M是公差带中心,μ是过程分布中心。USL是公差上限,LSL是公差下限。由前面学过的知识可知:
若此文能给大家带来豁然开朗的感觉,那就是本人的荣幸。有什么需要探讨的可与本人联系:13586957654
一、直方图与正态分布
描绘计量型数据的分布离不开直方图,下面先来回顾一下直方图的画法:
1、确定所要研究的对象,为了能更准确的反映总体的状况,至少收集100个数据。
2、计算数据的极差,极差=最大值-最小值。
3、确定分组数,一般来说可以按k=1+3.32lg(n)来定分组数,其中,n为样本量。
4、计算组距,
5、确定组界,组界由下组界和上组界构成。第一组的下组界为最小值-最小分度值的一半,第一组的上组界为第一组的下组界+组距,以此类推。
6、统计数据落入每组中的频数。
7、以组距为底,频数为高画直方,就可以得到一张直方图。
下面举一个画直方图的例子:
您在一家汽车工厂工作,目前正面临所用凸轮轴长度的变异性问题。您想了解由两家供应商提供的凸轮轴的质量是否相当,因此从每家随机抽取 100 件凸轮轴测量其长度。请分别给这两家供应商的数据画两张直方图。
手工画直方图比较繁琐,我们可以利用数据统计分析软件——Minitab来画直方图,画出的直方图如下:
从上面两张图可以发现:供应商1提供的凸轮轴的长度数据比供应商2的更加集中一点,表现为中间多两头少,而供应商2的数据就比较分散,凭直觉判断,我们应该选用供应商1的凸轮轴。
直方图有频数直方图和频率直方图,上面我们介绍的就是频数直方图。如果在画直方图时把频数替换为频率就成了频率直方图。频率是频数除以样本量,所以频率直方图就是频数直方图在坐标轴缩小“样本量”倍,但从形状上来看与频数直方图是一模一样的。
下面我们要在频率直方图的基础上来了解一下分布的概念。如果在画频率直方图时我们限定两个条件①收集的数据足够多;②分组数为无穷多组,大家想一想,这样画出来的直方图将会变成什么形状?
(直方图上的每个直方将会变成一条线)
每一条线的高度在数学上称为“概率密度”,如果用一条光滑的曲线把这些线的端点连接起来,就是我们平时所讲的分布曲线。所以分布曲线并不是很难理解的东西的,它实际上是概率密度函数在图形上的反映。
数据的分布形状有很多种类型,我们平时接触到最多也是最常用的分布是正态分布。分布的形状跟数据的类型有关。不同类型的数据具有不同的分布。数据通常分为两类:连续型数据(或者叫做计量型数据)和离散型数据(或者叫做计数型数据)。所谓连续型数据就是数据之间的间隔是可以无限细分的,比如长度是可以无限细分的,米可以分成分米,厘米,毫米,微米,纳米,……,所以长度就是一个连续型数据,体积、时间、压力等都是连续型数据。离散型数据是指不能无限细分的,它总存在一个最小的数据间隔,比如,不合格品数,它只能以“整”个来描述,不可能说成1.5个不合格品,2.5个不合格品,象这样一类的数据就是离散型数据,离散型数据还有很多,比如外观缺陷数,瑕疵数等等。
我们平时接触到最多也是最常用的分布是正态分布。正态分布也称高斯分布,它是由德国数学家高斯于1809年正式给出表达式的。为了纪念高斯的伟大贡献,在德国10马克的钞票上不但印上了高斯的头像,而且把正态分布曲线连同它的表达式印在钞票的正面。
正态分布的数学表达式为:
这个数学表达式中竖线后面的两个字母是正态分布的两个分布参数。μ是正态分布的分布中心, σ2是正态分布的方差,σ就是正态分布的标准差。我们只要知道这两个参数,一条正态分布曲线就可以把它确定下来。任何一条正态分布曲线都可以形象地描述为“中间高、两边低、左右对称、延伸到无穷”的钟形曲线。
分布中心反映了正态分布在横轴上的位置,而标准差反映了正态分布的离散状况,以下是不同分布中心和标准差的正态分布的比较。
有一类正态分布我们必须熟练应用,那就是标准正态分布。所谓标准正态分布就是分布中心为0,标准差为1的正态分布,任何一个正态分布都可以通过 数学变换转换成标准正态分布。以下就是一个分布中心为10,标准差为2的正态分布转换前后的图形。
下面我们来说说如何来计算μ和σ。μ和σ在数理统计上有专门的定义,但如果按照定义去求μ和σ的精确值几乎不大可能。我们通常是利用样本的状况去推断总体的状况,这在统计学上就称为参数估计。比如对于正态分布的中心和标准差,我们就可以用样本均值 和样本标准差s来估计。为了使估计值和精确值有所区分,我们用 分别表示μ和σ的估计值。
下面我们对上面提到的凸轮轴长度的数据再用正态分布曲线拟合一下,可以得到以下图形:
现在我们可以用数据来解释供应商1与供应商2之间的差异了:供应商 1 的凸轮轴似乎比供应商 2 的凸轮轴短。这可以从表格中的平均值(分别为 599.5 和 600.2)以及拟合正态分布峰值的相对位置看出来。
供应商 2 样本的标准差 (1.874) 远远高于供应商 1 的标准差 (0.6193)。这使得供应商 2 的拟合正态分布较低且较宽。供应商 2 的产品中大量变异性可能是导致凸轮轴长度不一致的主要原因。
二、过程输出与正态分布
过程输出 → 产品 → 产品可以用质量特性值来表示 → 质量特性值可分为计量型和计数型数据 → 数学理论上可以证明,如果某项计量型数据的指标受到很多项随机因素的干扰,而每项干扰都很小的话,则所有干扰影响的综合结果将导致此项指标的分布为正态分布
通过上面这段文字的指引,我们可以发现,如果过程的输出可以用计量型数据来表示的话,那么往往就可以用正态分布来表示过程的输出。正因为我们要了解过程的输出,而输出又可以用正态分布来表示,这就是我们为什么要学习正态分布的原因。
三、正态分布与过程不合格品率
也许生产控制人员最关心的问题就是产品的不合格品率。那么我们有没有办法通过正态分布来求产品的不合格品率呢?
假如有一个磨加工车间在磨一只产品,它的规范限是9.8—10.2,通过抽取样本画出的频率直方图如下:
图上的两条红线就是产品的规范限,从图上标明的数据很容易可以知道,这个样本中的不合格品率是0.01+0.01+0.02=0.04,也就是把所有超过规范限的“直方”加起来。而通过前面所学的知识我们知道,频率直方图上的一个直方在正态分布曲线图上就是一条线,如果要通过正态分布曲线来求不合格品率,只需把超出规范限以外的所有的“线”加起来,而所有的线加起来就构成了“面积”。所以利用正态分布求不合格品率就变成了求超出规范限以外的正态分布曲线与横轴所围成的面积。
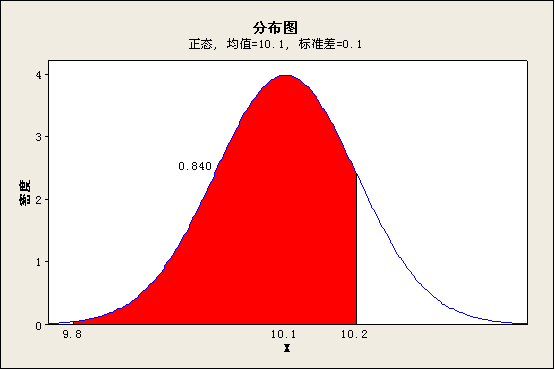
那么如何来求“超出规范限以外的正态分布曲线与横轴所围成的面积”呢?这个比较复杂,需要运用高等数学里的积分的方法求。但是我们可以借助MINITAB软件把它求出来。比如上面所举的例子,磨加工高度的规范限是9.8—10.2,现在通过抽取样本计算出均值为10.1,标准差为0.1,我们可以先通过正态分布求出该磨加工过程的合格品率。
通过上图可知,该磨加工过程的合格品率为84%,那么不合格品率就是16%。
假如通过改进过程,使得过程的平均值靠近公差带中心,即10,我们再来看一下过程的不合格品率会发生什么变化。
这时,过程的合格品率就提高到了95.4%,而不合格品率就降低为4.6%。
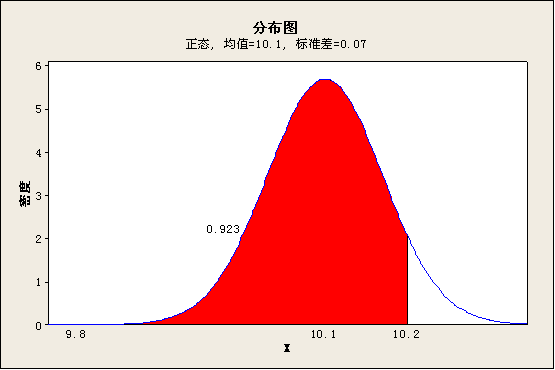
如果过程的均值没有发生变化,但设法提高了过程的加工精度,标准差由0.1减小为0.07,我们再来看一下过程的不合格品率又发生了什么变化。
我们可以发现合格品率由84%提高到了92.3%,而不合格品率降为7.7%。
最后我们得出减小过程不合格品率的两种策略:
在产品的公差范围不变的情况下,通过改进过程,使得过程的均值向公差带中心靠拢和/或减小过程的变差,可以显著地减小过程的不合格品率。
在两种策略中,相比较而言,让过程均值向公差带中心靠拢更容易实现一些。所以在过程不合格品率过大的情况下,首先要分析一下过程均值有没有跟公差带中心靠拢,然后再设法提高加工的精度。
四、过程能力指数
通过上面的介绍,我们知道,过程是可以用分布来描述的。而分布有它的一些特定的参数,比如分布中心和标准差。分布参数不同,满足顾客要求的能力也不同。比如标准差大的比标准差小的满足顾客要求的能力要差,因为标准差大的过程产生的不合格品会多一些。我们通常把6倍的标准差称为过程的能力。把过程能力与顾客的要求(即公差范围)去比较,称为过程能力指数。所以过程能力指数是表征过程满足顾客要求的能力的指标。
过程能力指数的计算公式是:
但是,如果标准差相同,分布中心不同,这两个过程满足顾客要求的能力也是不同的。如下图所示,两个过程标准差相同,但分布中心相差ε,这两个过程的不合格品率也是不同的。
如果光从Cp来表示还不能区分这两个过程满足顾客能力的大小,所以又增加了一个指数Cpk:
其中ε为过程分布中心偏离公差带中心的距离。
对Cpk的算式进行简单处理,可以得到如下等式:
令:T=USL-LSL
接下来的问题是,如何来估计总体的标准差σ?在解决这个问题之前,我们先要了解一下稳定的和不稳定的过程。
所谓稳定的过程是在任何一个时刻去观测过程,它的分布位置和分布宽度都是恒定不变的。如下图所示的就是一个稳定的过程。它的特点是过程的均值和标准差都保持不变。
而不稳定的过程是指在不同的时刻去观测过程,它的分布位置和分布宽度都可能会发生变化。如下图所示的就是一个不稳定过程。
对于不稳定的过程,任一时刻的过程的输出的标准差都可能会不同,用任一时刻的过程输出的标准差来代表整个过程的标准差都是片面的,不合理的。因此计算过程能力指数有一个前提条件,那就是:过程必须预先用控制图来判断是稳定的。在这种状态下可以用 来估计σ,其中 是控制图当中的极差平均值, 是一个跟子组大小有关的系数,可查表。比如当子组大小为5的时候, 。
在这时候过程能力指数就可表示为:
可是如果过程确实是不稳定的怎么办?这时候我们可以用合并的标准差,也就是样本标准差s来估计总体的标准差。
当σ用s来估计时,得到的就不是过程能力指数,而是过程性能指数Ppk。
接下来我们来看看
和6s有什么区别。我们用图示的方法来说明。
对于稳定的过程,任一时刻的输出的中心和分布宽度基本上是不变的。如果把某一时刻的过程输出当成一个子组,那么每个子组之间只存在着组内波动, , ,……,表示的就是组内波动。它不存在着组与组之间的波动。而且组内的波动也是相等的,只是由于抽样的缘故,它们之间会存在略小的差别。总的过程波动可以用各个组内波动的平均 来估计。从波动引起的机理上来说,组内波动主要由偶然因素引起,组间波动由异常因素引起。所以稳定的过程也可以说是只有偶然因素在起作用的过程。而不稳定的过程是除了组内波动以外,还有组间波动,组间波动主要表现为子组的分布中心发生了漂移,而且从上图可以看出组内的波动也可能是不相等的。不稳定的过程是除了偶然因素在起作用以外还有异常因素在起作用的过程。所以总的过程标准差必须用合并的标准差,即样本标准差s来估计。这个s既包括了偶然因素引起的波动,又包括了异常因素引起的波动,最后计算出来的s应该比其中任何一个都要大。如果一个过程计算出的s与 差不多大,那么我们也可以大致推断过程是稳定的。
正因为 与6s存在上面这样的一种关系,所以从理论上来说过程性能指数Ppk总要比Cpk小。
因为在实际过程运行中,稳定是相对的,变化是绝对的。不发生变化(这种变化是由于异常因素在起作用而引起)的过程几乎是不可能,即便是稳定的过程,也只能是保持在相对来说比较长的一段时间内。所以我们有时把过程能力指数称为短期过程能力指数,把过程性能指数称为长期过程能力指数。
如果把一个过程比作一个人的话,那么一个稳定的过程就相当于是一个精神正常的人,而一个不稳定的过程就象是一个有精神病的人,我们谁都希望跟精神正常的人打交道,谁都不愿意跟精神不正常的人相处。因为我们对一个精神病人的行为是无法把握的,这就会增加我们心中的恐惧感。让过程处于稳定受控状态是现场控制人员的一项重要任务。上面我们也提到,过程总有一种由稳定向不稳定变化的趋势,怎么样发现过程已经开始发生变异是采取措施的关键。控制图就是帮助我们识别过程发生变异的重要工具。如果我们在控制图上规定一些采取措施的“行动点”,及时对开始变异的过程加以调整,我们是完全能够使过程处于稳定状态的。
下面举一个利用MINITAB进行过程能力分析的例子。
某台机器连续生产钢珠,直径是它的一个重要质量特性。为对钢珠直径进行控制,每隔15分钟抽样1次,每次抽取产品5个,共抽样25次。测量并记录数据。经检验钢珠直径服从正态分布,试绘制Xbar—R控制图并进行过程能力分析。
首先是利用MINITAB画出控制图,判断这个过程是否处于稳定状态。
丛图上可知,所有的点都在控制限内,并且也没有非随机的趋势,因此我们可以判断生产过程处于稳定状态。接下来我们进行过程能力的分析。
观察上图,可以获得很多信息。首先,图正中带两条拟合曲线的直方图给了我们最直观的认识。两条线几乎完全重合,将左上角的标准差(组内)=0.024841与标准差(总体)=0.024722相比,相差甚微,这说明除了组内的偶然因素引起的波动以外,几乎不存在组间波动。其次,Cp=0.67,Cpk=0.67,两者均小于1.33,说明过程能力不足,需要改进过程,两者没有差别,说明主要改进方向是设法降低过程的偶然因素引起的波动。再次,图左下方的PPM值的统计从可能出现的不良率这个角度解释了过程能力的优劣。
五、过程能力指数和不合格品率之间的关系
从过程能力指数的计算公式
可知,提高过程能力指数的途径有三种:
1、增大公差范围。
2、减少分布中心和公差带中心的偏移量。
3、减少过程输出的标准差。
在上面讲到不合格品率的内容时,我们也分析了减少不合格品率的途径。通过对比,我们发现减少不合格品率与提高过程能力指数的途径是一样的,这说明两者之间肯定存在着千丝万缕的联系。那么它们之间到底存在着什么样的精确关系呢?下面就为大家来解析这个问题。
上图中α为超出公差下限的不合格品率,β超出公差上限的不合格品率。M是公差带中心,μ是过程分布中心。USL是公差上限,LSL是公差下限。由前面学过的知识可知:
若此文能给大家带来豁然开朗的感觉,那就是本人的荣幸。有什么需要探讨的可与本人联系:13586957654
 TA的首页
TA的首页