为什么 30 个样本就称为「大样本」，而不是 40 或 50？

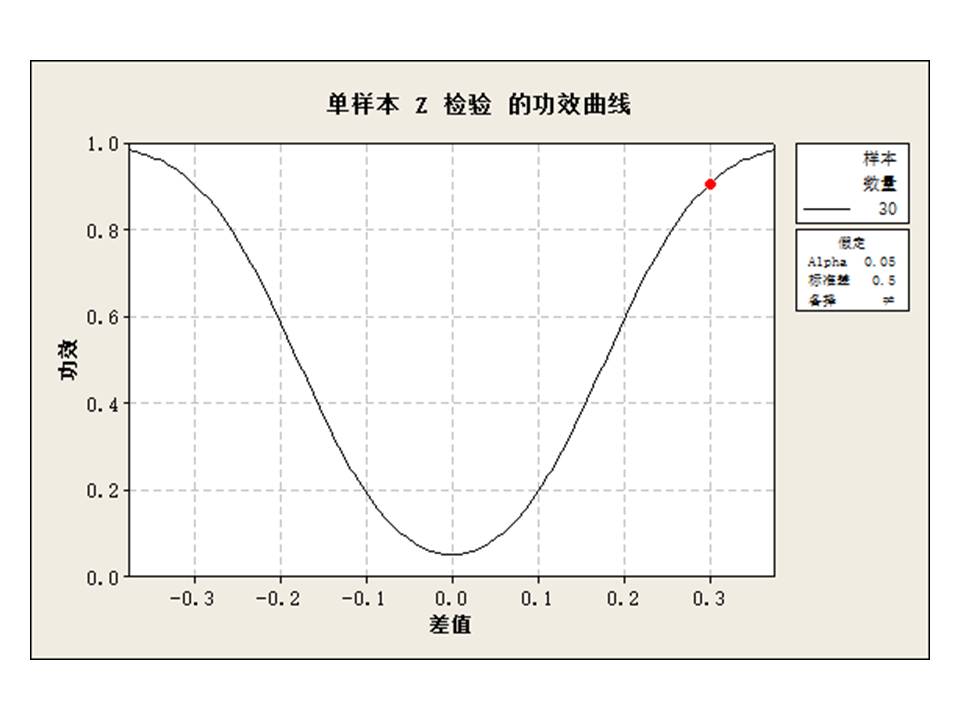
样本数的决定取决于需要预测的精度。预测精度简单理解就是能够容忍的差是多少，可以表现为标准偏差的差，也可以表现为百分比的差。也就是 ▏μ-M ▏允许差多少。μ为总体的均值，M为抽样得到的均值。差越小，抽样数就越需要多。如果允许10%的预测误差的话， 就是 ▏μ-M ▏/μ<10%，这通常被认为是一种稳定的状态。那么也就是最大误差不能超过0.1倍总体的偏差。总偏差的宽度是6个标准偏差，那么允许的误差就应该是五分之三标准偏差。按照这样的精度要求计算,样本数是30。所以，30个样本数就是这样产生的。在计算技术不发达的初期，为了能够让普通人都能运用统计手法，统计学家制定了这样的一个方案

关于如何计算样本数，有以下公式计算得到，α=0.05、β=0.1。有兴趣的可以计算一下。

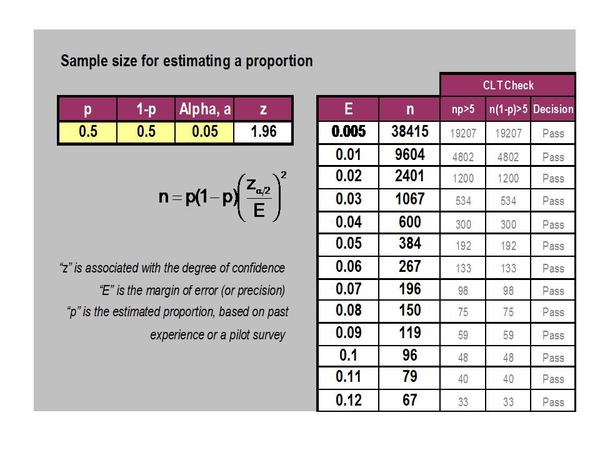
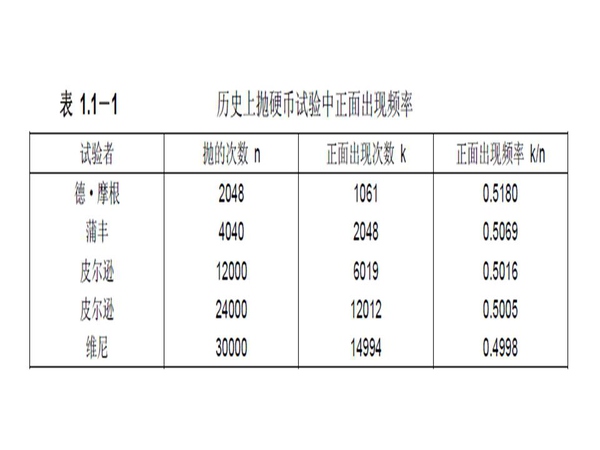
在实际当中需要多少样本数才能反映总体呢？比如：抛硬币，有人曾问过这样的问题，就是抛了10次都是正面，那么第11次是正面的概率是多少。。。抛硬币时候确实会有连续是某一面的情况存在，但这并不是它本质的概率。如果获得准确的本质概率需要抛多少次才能反映呢？抛11次，得到某一面出现为50%的结论的概率只有70%。如果要达到99%准确的话，则需要试验9604次试验。因此样本需要多少，完全取决于需要达到多少预测的精度。

上表就是样本数量的一个计算表，E代表的是我们可以忍受的误差。抛硬币试验，历史上有好多人都做过试验，结果证实了以上的计算结果。

著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
在网上找到了一篇文章贴上，供参考：如何确定样本量,基本方法很多,但是公式检验表明,当误差和置信区间一定时,不同的样本量计算公式计算出来的样本量是十分相近的,所以,我们完全可以使用简单随机抽样计算样本量的公式去近似估计其他抽样方法的样本量,这样可以更加快捷方便,然后将样本量根据一定方法分配到各个子域中去.所以,区域二相抽样不能计算样本量的说法是不科学的.　　1．简单随机抽样确定样本量主要有两种类型: 　　（1）对于平均数类型的变量　　对于已知数据为绝对数,我们一般根据下列步骤来计算所需要的样本量.已知期望调查结果的精度(E), 期望调查结果的置信度(L),以及总体的标准差估计值σ的具体数据,总体单位数N. 计算公式为:n=σ2/(e2/Z2+σ2/N) 特殊情况下,如果是很大总体,计算公式变为:n= Z2σ2/e2 例如希望平均收入的误差在正负人民币30元之间,调查结果在95%的置信范围以内,其95%的置信度要求Z的统计量为1.96.根据估计总体的标准差为150元,总体单位数为1000. 样本量:n=150*150/(30*30/(1.96*1.96))+150*150/1000)=88 (2)于百分比类型的变量 对于已知数据为百分比,一般根据下列步骤计算样本量.已知调查结果的精度值百分比(E),以及置信度(L),比例估计(P)的精度,即样本变异程度,总体数为N. 则计算公式为:n=P(1-P)/(e2/Z2+ P(1-P)/N) 同样,特殊情况下如果不考虑总体,公式为:n= Z2P(1-P)/e2   一般情况下,我们不知道P的取值,取其样本变异程度最大时的值为0.5. 例如:希望平均收入的误差在正负0.05之间,调查结果在95%的置信范围以内,其95%的置信度要求Z的统计量为1.96,估计P为0.5,总体单位数为1000.样本量为:n=0.5*0.5/(0.05*0.05/(1.96*1.96)+0.5*0.5/1000)=278 2.样本量分配方法 　　以上分析我们获得了采用简单随机抽样公式计算得到的样本量,总的样本量需要在此基础上乘以设计效应的值得到.由于样本总量已经确定,我们采用总样本量固定方法分配样本,这种方法包括按照比例分配和不按照比例分配两类.实际工作中首先计算取得区县总的样本量,然后逐级将其分配到各阶分层中,如果不清楚各阶分层的规模和方差等,一般采取比例分配或者比例平方根分配法.如果有一定辅助变量可以使用,可以采用按照规模分配法分配样本量. 　　3.样本量和总体大小的关系: 　　在其它条件一定的情况下,即误差、置信度、抽样比率一定,样本量随总体的大小而变化.但是,总体越大,其变化越不明显；总体较小时,变化明显.  　　二者之间的变化并非是线性关系.所以,样本量并不是越大越好,应该综合考虑,实际工作中只要达到要求就可以了.结论：样本大小与我们期望的预测精度以及总体大小有关，预测精度越高，样本量就越大。。。直至百分百的调查。为保证95%的置信度，我们通常认为至少30组数据为抽样调查的样本数。如果一组是5个数据的话，那么一般就按照125执行。总体数小于3000的情况下，我们基本上就可以按照125样本数实施。