1分钟教你制作单样本Z检验

对九个小配件进行了测量。您知道，根据历史经验，测量值的分布接近于正态，且 s = 0.2。由于已知 s，并且要检验总体均值是否为 5 并获得均值的 90% 置信区间，因此使用 Z 检验。
 
数据如下:
值
4.9
5.1
4.6
5.0
5.1
4.7
4.4
4.7
4.6
 
操作:
1, 6SQ统计--估计和假设检验--单样本Z检验


 
2，置信水平输入 90% 假设均值 5  总体标准偏差0.2 
 备择假设选择 不等于 . 图表选择 数据单值图。

 
3,点击确认输出结果:



解释结果

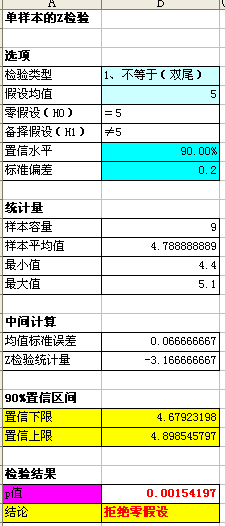
用于检验总体均值是否等于 5 的检验统计量 Z 为 -3.17。p 值 或在原假设为真时否定原假设的概率为 0.0015。这称为达到的显著水平 、p 值或检验达到的 a。由于 p 值 0.0015 小于通常选择的 a 水平 ，有显著证据表明 m不等于 5，因此否定 H0，支持 m 不等于 5。

通过查看单值图还可以执行 a = 0.1 时的假设检验 。假设值落于总体均值的 90% 置信区间 (4.6792, 4.8985) 之外，因此可以否定原假设。

excel案例数据
http://pan.baidu.com/s/1i5AXSRN​
6SQ统计3.0企业版90天试用下载​ http://pan.baidu.com/s/1i5AXSRN