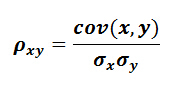“爹矮矮一窝”的说法正确吗？相关分析法告诉你！

 全世界父母关注的事
        没有听说哪个父母希望孩子越矮越好，都希望子女““高大上”。但中国民间一直流传着这样的说法。“娘矮矮一个，爹矮矮一窝”，这句话靠谱吗？



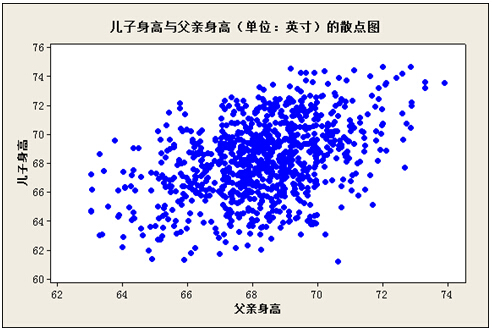
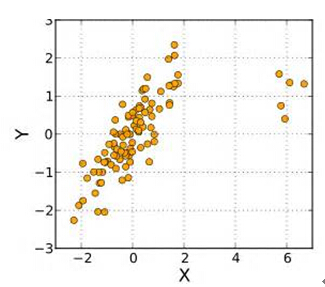
       其实，这种困扰不止在中国有，在外国也有。为此，一百多年前（1900年前后），人类学家、优生学家、英国皇家学会院士佛朗西斯.高尔顿（Francis Galton）爵士和有统计学之父尊称的卡尔·皮尔森（Karl Pearson）等人对此进行了调查研究。他们对英格兰市民进行了抽样调查，得到1078对成年父子身高的数据，并画出以下散点图：



       从这个图形可以看到，随着父亲身高变高，儿子的身高确实有变高的趋势。我们把一个连续变量（y）随着另外一个连续变量（x）增加而增加或减少的现象叫做相关。如果y随x增加而增加，就称y与x为正相关；如果y随x增加而减少，就称y与x为负相关。儿子的身高与父亲的身高即为正相关关系，即：父亲身高高的话，儿子身高就会高。
 
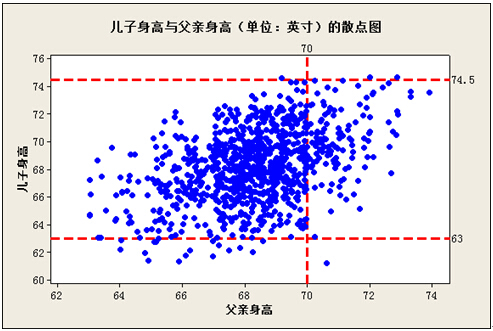
另一方面，我们也看到，儿子身高随父亲身高增加得并没有那么紧密。请下图：



       当父亲身高为70英寸时，儿子身高从63英寸到74.5英寸都有可能，其变化范围多达11.5英寸。换句话说，儿子身高与父亲身高的相关性并没有那么强！为此皮尔森定义了相关系数（即皮尔森系数，总体用ρ，样本用r标示），以表达变量间的相关强度。



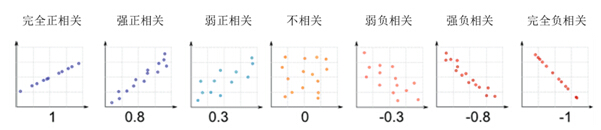
       相关系数的取值范围为（-1,1），r的绝对值越大，相关性就越强。r=1为完全正相关，r=-1为完全负相关，r=0意味着没有线性相关关系。



       经过计算，这1078对父子身高的相关系数r=0.419,属于偏弱的相关性。那么结论就出来了，父亲的身高确实对儿子的身高有影响，但影响比较弱。看来“爹矮矮一窝”的说法并不靠谱！千百年来，父亲们受到了很多错怪，承受了很多不公正的压力！

相关性分析的基本方法

        相关分析是针对连续变量之间的关系进行分析。其基本分析方法为散点图和相关系数。散点图就是把两个变量的坐标点画在直角坐标系中，观察其形状，以判断其相关属性：正相关、负相关和不相关（无线性相关）。从这些点的集中和离散程度可以判断其相关强度。但这样判断相关强度并不准确，因此相关系数是判断相关强度的准确方法。

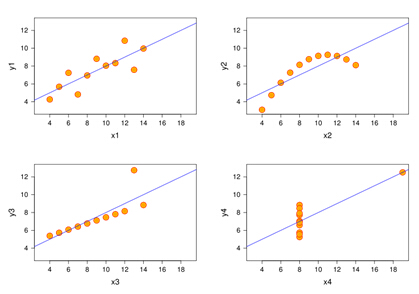
       但不能仅仅依靠相关系数判断变量间的相关强度。下图中4对变量的散点图各不相同，但它们的相关系数均为0.816。因此相关分析必须是先分析散点图，再计算相关系数，否则可能得到错误的结论。



相关分析的注意事项

 相关不一定有因果分析。研究指出，医院规模增加，病人死亡率亦显著提升。这么说来，我们应该避免去大型医院就诊吗？显然这是一个不合理的结论。



相关关系不能外推。相关关系的存在只限于研究的范围，把相关关系的结论外推到超出研究的范围，可能导致错误的结论。如二手汽车的售价会随着车龄增加而降低，车的售价与车龄属于负相关的关系。但这个结论一般只在一定的车龄范围内有效，超过一定的车龄范围（如50年），售价和车龄的关系未必就是负相关关系了，也许变成正相关关系。



异常点的处理。出现异常点时，要调查原因，再进行处理。不处理异常点或直接把异常点删除都可能导致错误的后果。


版权声明：本文由科理咨询原创，版权归属科理咨询，抄袭必究。