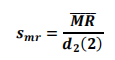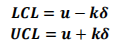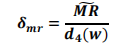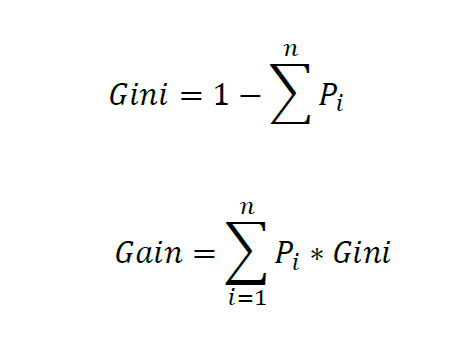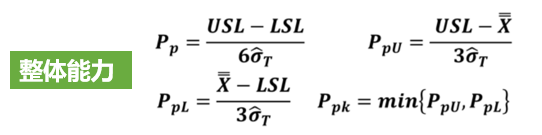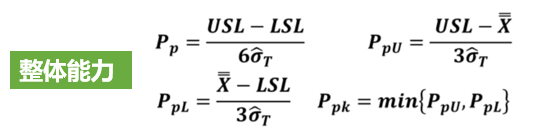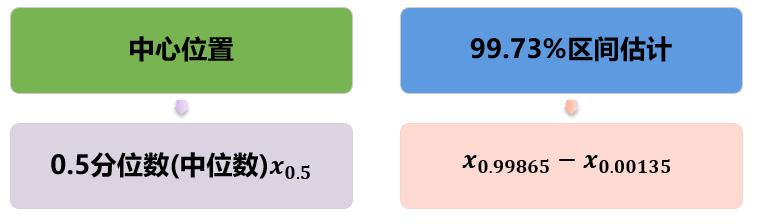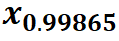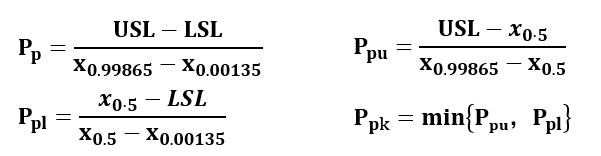创建蒙特卡洛模拟的 4 个简单步骤
20 世纪 40 年代,研究原子弹的科学家应用 Monte Carlo 模拟计算了一个裂变铀原子引起另一个裂变反应的概率,这是该模拟的首次应用,自此以来已经取得了很大进展。今天我们将介绍如何使用 Minitab 为已知的工程公式和 DOE 方程创建 Monte Carlo 模拟。
由于当时铀供应短缺,试验的试错空间很小,因此 Monte Carlo 模拟一直专注于根据模拟数据计算可靠的概率。如今,从材料工程到医疗设备包装密封再到炼钢,模拟数据经常用于许多场景,例如资源有限的场景,或者收集真实数据过于昂贵或不切实际的场景。使用 Engage 或 Workspace 的 Monte Carlo 模拟工具可以:
(1)模拟可能结果的范围以帮助做出决策
(2)预测财务结果或估计项目时间表
(3)了解过程或系统中的变异性
(4)在过程或系统中发现问题
(5)通过了解成本/效益关系来管理风险
开始使用任何 Monte Carlo 模拟的4 个步骤
模拟可能非常复杂,具体取决于所涉及因子的数量。但所有 Monte Carlo 模拟基本上都有四个简单的步骤:
• 确定传输方程
要创建 Monte Carlo 模拟,您需要一个包含要探索的业务活动、计划或过程的定量模型。过程的数学表达式称为“传输方程”。这可以是已知的工程或业务公式,也可以基于根据设计试验 (DOE) 或回归分析创建的模型。借助 Minitab Engage 和 Minitab Workspace 等软件,您能够创建复杂的方程,甚至是具有多个可能相互依赖的响应的方程。
• 定义输入参数
对于传输方程中的每个因子,确定其数据的分布方式。一些输入可能遵循正态分布,而另一些则遵循三角分布或均匀分布。然后,您需要确定每个输入的分布参数。例如,需要为遵循正态分布的输入指定均值和标准差。如果您不确定数据遵循哪种分布,可以使用 Engage 和 Workspace 提供的工具来确定。
• 设置模拟
要进行有效的模拟,您必须为每个输入创建一个非常大的随机数据集(大约包含 100,000 个实例)。这些随机数据点模拟在很长一段时间内,对于每个输入将看到的值。尽管听起来工作量很大,但这正是 Engage 和 Workspace 的亮点。一旦我们提交输入和模型,一切都会得到处理。
• 分析过程输出
有了模拟数据,您就可以使用传输方程来计算模拟结果。考虑到输入中的预期变异,通过模型运行足够多的模拟输入数据将可靠地指出该过程将在一段时间内输出的内容。
Monte Carlo 使用已知工程公式的4 个步骤
一家制造公司需要评估所提议产品的设计,这是一款每分钟必须泵送 12 毫升流体的小型活塞泵。考虑到活塞直径 (D)、冲程长度 (L) 和每分钟冲程数 (RPM) 的自然变异,您想要估计数千个泵的可能性能。理想情况下,数千个泵的泵流量将具有不大于 0.2 毫升的标准差。
• 确定传输方程
进行 Monte Carlo 模拟的第一步是确定传输方程。在本例中,您只需使用已知的工程公式来测量泵流量:
流量(以毫升为单位)= π(D/2)2 ∗ L ∗ RPM
• 定义输入参数
现在,必须定义传输方程中使用的每个输入的分布和参数。泵的活塞直径和冲程长度是已知的,但必须计算达到所需 12 毫升/分钟流速所需的每分钟冲程数 (RPM)。每个冲程泵送的体积按以下方程计算:π(D/2)2 * L
如果 D = 0.8,L = 2.5,则每个冲程排出 1.256 毫升流体。因此,要达到 12 毫升/分钟的流速,RPM 为 9.549。
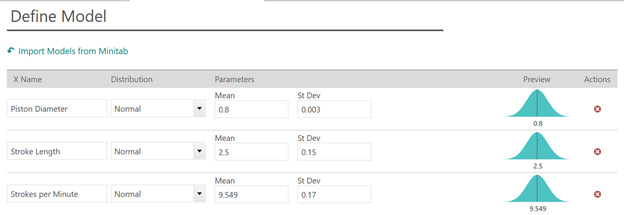
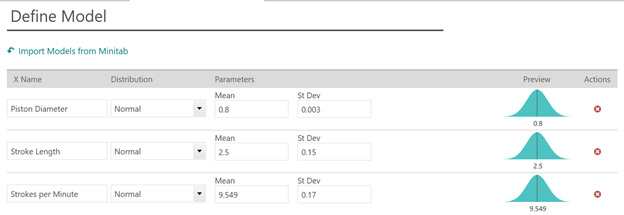
根据贵厂制造的其他泵的性能,您可以假定活塞直径呈正态分布,均值为 0.8 厘米,标准差为 0.003 厘米。冲程长度呈正态分布,均值为 2.5 厘米,标准差为 0.15 厘米。最后,每分钟冲程数呈正态分布,均值为 9.549 RPM,标准差为 0.17 RPM。
• 在 Engage 或 Workspace 中设置模拟
单击顶部功能区中的插入选项卡,然后选择 Monte Carlo 模拟。
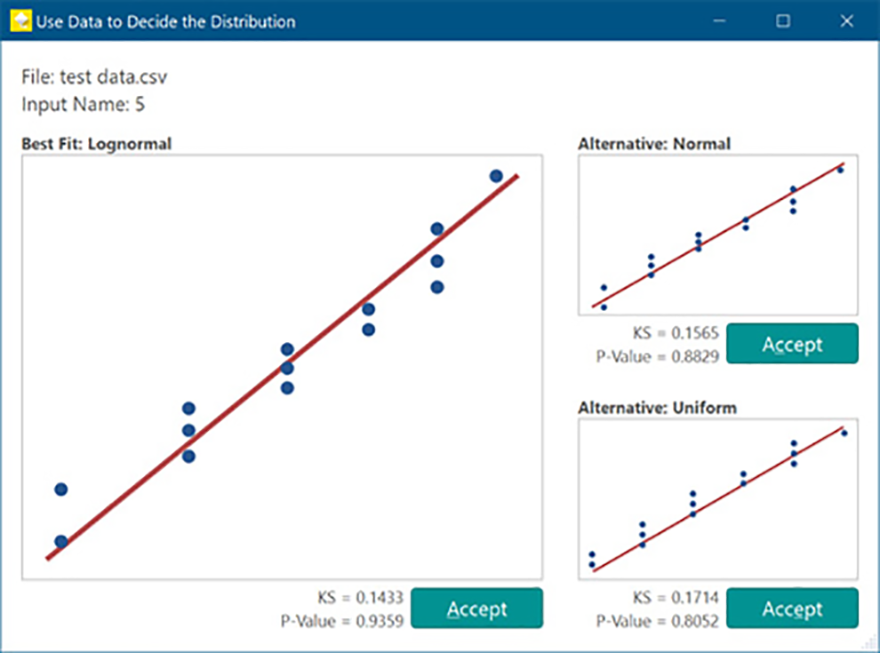
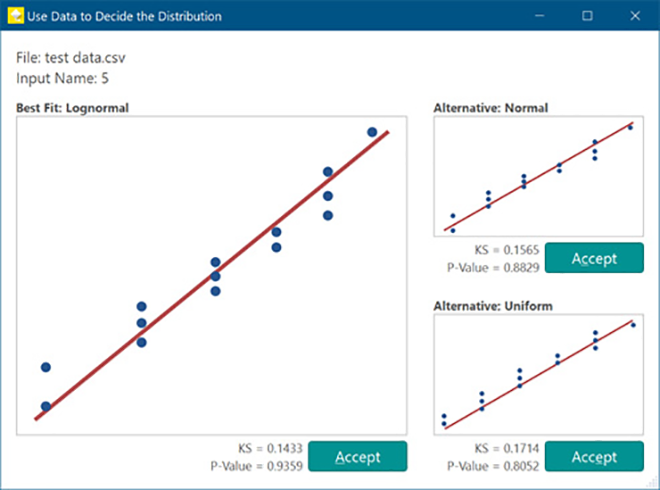
我们将它变得非常简单 — 您只需为每个变量提供名称,从下拉菜单中选择一个分布,然后输入参数。我们将按照上面所述的内容进行操作。如果您不确定数据遵循哪种分布,可以选择使用数据确定。这将提示您上传数据的 .csv 文件,可从以下几个选项中进行选择:
• 模拟和分析过程输出
下一步是给出方程。在这里,操作非常简单,只需为您的输出提供名称(我们提供的名称是 Flow),然后键入我们在上面确定的正确传输方程。您还可以添加规格上限和规格下限以查看模拟的比较情况。
然后,在功能区中,选择要运行的模拟数量(100,000 是不错的基准),然后单击用来运行模拟的按钮。
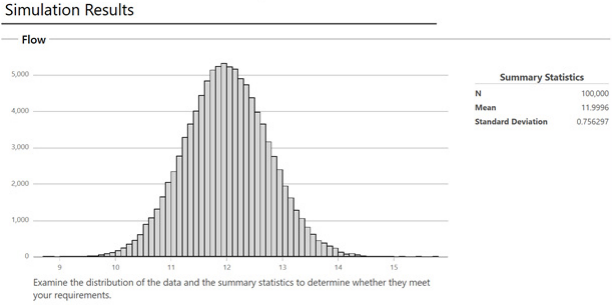
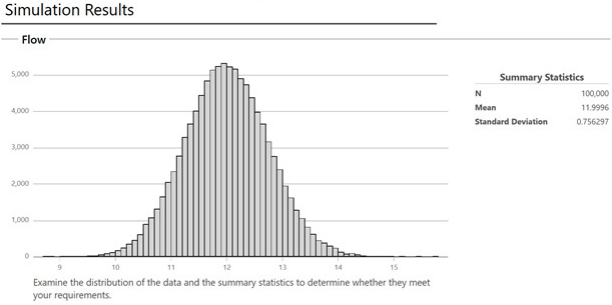
对于为了撰写本文而生成的随机数据,基于 100,000 个样本的平均流速为 11.996。从平均值来看,我们达到了目标,但最小值为 8.7817,最大值为 15.7057。这是一个相当大的范围。(所有组件的)传输变异导致标准差为 0.756 毫升,这远远超过目标值 0.2 毫升。
看起来这种泵的设计变异太大,需要在投入生产之前进一步完善。从这里,我们看到模拟所带来的好处。如果我们直接投入生产,很可能会生产出太多被退货的泵。借助 Monte Carlo 模拟,我们能够解决所有这些问题,而不会因制造和测试数千个原型或过早投入生产而产生费用。
您可能想了解这些模拟结果是否站得住脚,不妨自己尝试一下吧!运行不同的模拟将导致轻微的变化,但每次的最终结果(流速变异量不可接受)都会保持一致。这就是 Monte Carlo 方法的强大之处。
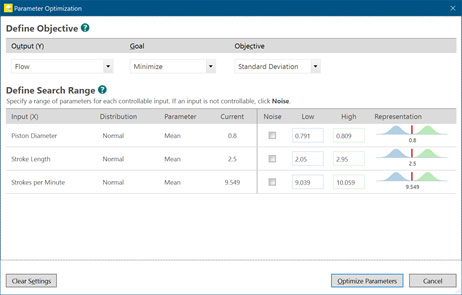
另一个可选步骤:参数优化
了解到标准差过高非常有价值,但 Engage 和 Workspace 真正突出的地方在于它们能够帮助改善状况。这就是参数优化的用武之地。
让我们看看第一个输入:活塞直径。平均值为 0.8,大部分数据将接近该值,或者在平均值的一两个标准差内。但是,如果活塞直径越小,流动效率越高,该怎么办?参数优化有助于我们回答这个问题。
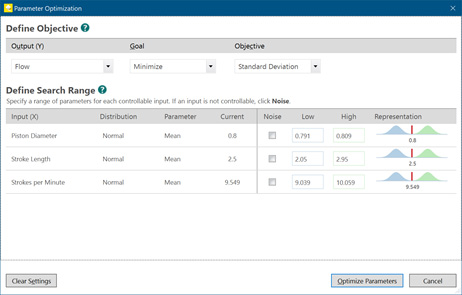
为了进行参数优化,我们需要为每个输入指定搜索范围。在本例中,为简单起见,我指定的算法搜索范围是 +/- 3 个标准差。然后,Engage 或 Workspace 将帮助我们为每个输入找到要实现目标(在本例中是减小标准差)的最佳设置。选择合适的范围至关重要;确保您输入的整个范围都可以运行;如果找到的最佳解决方案无法在生产环境中复制,则毫无用处。
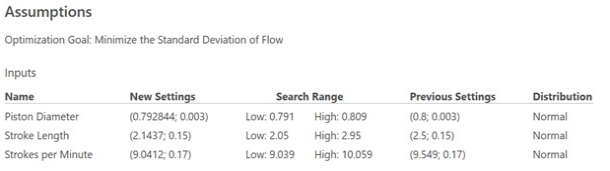
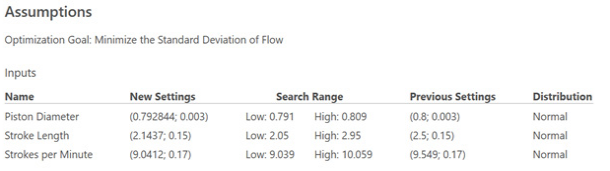
如果您在 Minitab Statistical Software 中用过响应优化器,则原理类似。下面是我们的结果:
基于以上结果,如果要减小标准差,则应当减小冲程长度和每分钟冲程数。活塞直径可以保持类似大小。请记住,Monte Carlo 模拟的关键之处在于,能够在不构建单个新原型或进行新试验的情况下找出所有这些结果。
Monte Carlo 使用试验设计 (DOE) 响应方程
如果您不知道要使用什么方程,或者您正在尝试模拟独特过程的结果,该怎么办?此时,我们可以将 Minitab Statistical Software 的设计试验功能与 Engage 或 Workspace 的模拟功能相结合。
一家电子制造商已指派您改进其电极清洁操作,该操作为电镀金属部件做准备。制造商通过电镀在原材料上涂上一层不同的金属,以实现所需的特性。电镀不会附着在肮脏的表面上,因此该公司有一个连接到自动电镀机的连续流电极清洗系统。传送带将每个部件浸入槽中,槽中的电压通过部件传送,从而对部件进行清洁。如果清洁不充分,会导致平均粗糙度的均方根(简称 RMS)值太高以及表面光洁度较差。经过正确清洁的部件具有光滑的表面和较低的 RMS。
为了优化该过程,可以调整两个关键输入:电压 (Vdc) 和电流密度 (ASF)。对于电极清洁方法,Vdc 的典型工程限值为 3 至 12 伏。电流密度限值为 10 至 150 安培/平方英尺 (ASF)。
• 确定传输方程
您不能针对该过程使用教材上的已知公式,但可以在 Minitab 中设置响应曲面 DOE 以确定传输方程。响应曲面 DOE 通常用于通过为“关键少数”可控因子寻找最佳设置来优化响应。
在本例中,响应将是部件在清洁后的表面质量。
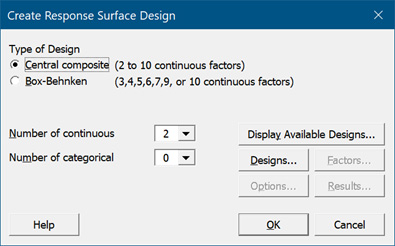
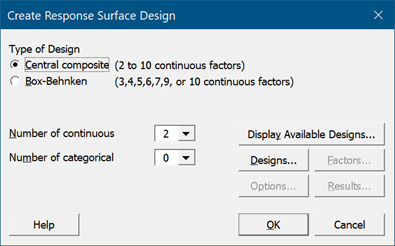
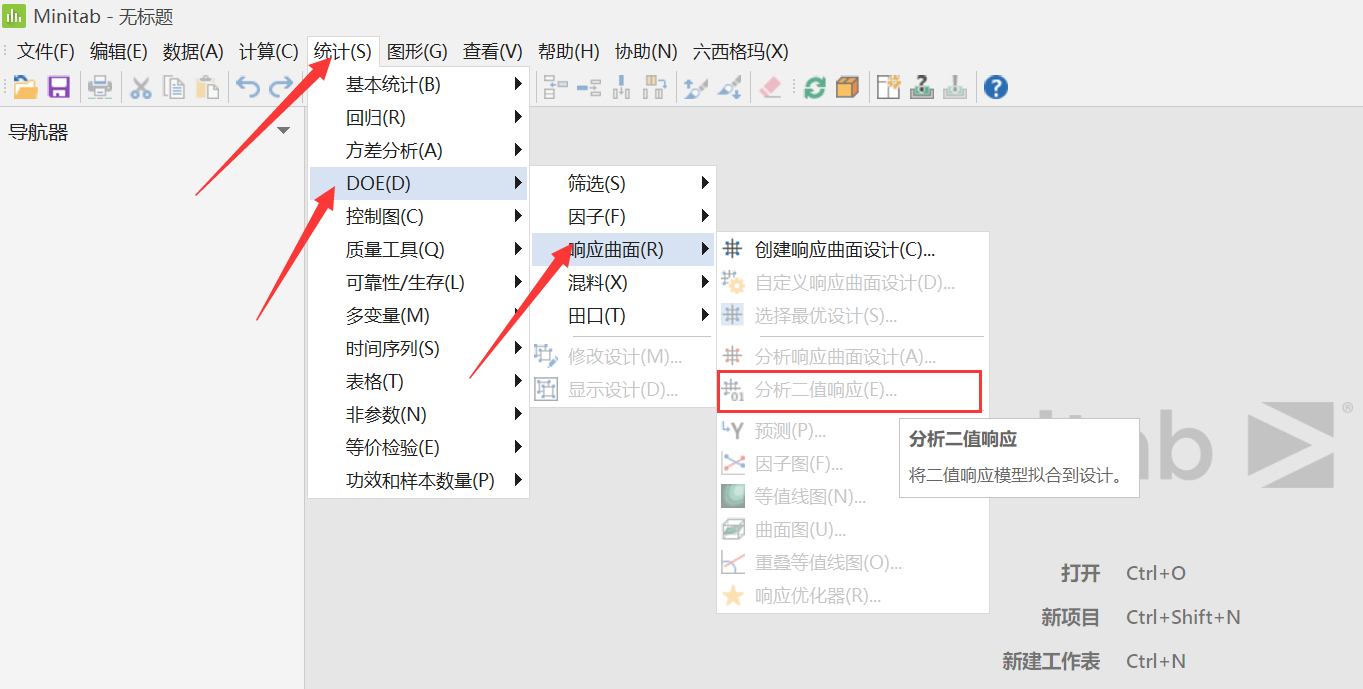
要在 Minitab 中创建响应曲面试验,请选择统计 > DOE > 响应曲面 > 创建响应曲面设计。由于我们有两个因子(电压 (Vdc) 和电流密度 (ASF)),因此我们将选择试验次数为 13 的双因子中心复合设计。
Minitab 创建设计试验后,您需要执行 13 次试验、收集数据并记录 13 个清洁后部件的表面粗糙度。通过 Minitab,可轻松分析 DOE 结果、简化模型和使用残差图检查假定。使用最终模型和 Minitab 的响应优化器,可以找到变量的最佳设置。在本例中,您将电压设置为 7.74,将 ASF 设置为 77.8,所获得的粗糙度值为 39.4。
响应曲面 DOE 为 Monte Carlo 模拟生成以下传输方程:
粗糙度 = 957.8 − 189.4(Vdc) − 4.81(ASF) + 12.26(Vdc2) + 0.0309(ASF2)
• 定义输入参数
现在,您可以为Monte Carlo模拟输入设置参数定义,并将它们带入Engage或Workspace 中。
请注意,标准差必须已知或基于现有的过程知识进行估计。这适用于所有 Monte Carlo 输入。电压呈正态分布,均值为 7.74 Vdc,标准差为 0.14 Vdc。每平方英尺安培数 (ASF) 呈正态分布,均值为 77.8 ASF,标准差为 3 ASF。
• 在 Engage 或 Workspace 中设置模拟
这与步骤 3 完全相同。单击功能区中的插入 > Monte Carlo 模拟,添加您的输入并定义其参数,然后输入您的模型。在本例中,如果您拥有最新版本的 Minitab,则可以单击鼠标右键,然后点击发送到 Engage 或发送到 Minitab Workspace。如果您没有,则可以从 Minitab 输出中手动复制它并将其粘贴到 Engage 或 Workspace 的模型字段中。
• 模拟和分析过程输出
汇总表明,即使基础输入呈正态分布,RMS 粗糙度的分布也不是正态的。该汇总还显示所有组件的传输变异导致标准差为 0.521,根据您掌握的过程知识判断,这是不错的过程结果。基于试验次数仅为 13 的 DOE,我们可以确定在该过程中将看到的实际情况。同样,由于这基于模拟数据,您的答案会略有不同,但通常而言答案应该是正确的。如有必要,我们可以查看参数优化以微调我们的答案并找到最佳解决方案。 收起阅读 »
由于当时铀供应短缺,试验的试错空间很小,因此 Monte Carlo 模拟一直专注于根据模拟数据计算可靠的概率。如今,从材料工程到医疗设备包装密封再到炼钢,模拟数据经常用于许多场景,例如资源有限的场景,或者收集真实数据过于昂贵或不切实际的场景。使用 Engage 或 Workspace 的 Monte Carlo 模拟工具可以:
(1)模拟可能结果的范围以帮助做出决策
(2)预测财务结果或估计项目时间表
(3)了解过程或系统中的变异性
(4)在过程或系统中发现问题
(5)通过了解成本/效益关系来管理风险
开始使用任何 Monte Carlo 模拟的4 个步骤
模拟可能非常复杂,具体取决于所涉及因子的数量。但所有 Monte Carlo 模拟基本上都有四个简单的步骤:
• 确定传输方程
要创建 Monte Carlo 模拟,您需要一个包含要探索的业务活动、计划或过程的定量模型。过程的数学表达式称为“传输方程”。这可以是已知的工程或业务公式,也可以基于根据设计试验 (DOE) 或回归分析创建的模型。借助 Minitab Engage 和 Minitab Workspace 等软件,您能够创建复杂的方程,甚至是具有多个可能相互依赖的响应的方程。
• 定义输入参数
对于传输方程中的每个因子,确定其数据的分布方式。一些输入可能遵循正态分布,而另一些则遵循三角分布或均匀分布。然后,您需要确定每个输入的分布参数。例如,需要为遵循正态分布的输入指定均值和标准差。如果您不确定数据遵循哪种分布,可以使用 Engage 和 Workspace 提供的工具来确定。
• 设置模拟
要进行有效的模拟,您必须为每个输入创建一个非常大的随机数据集(大约包含 100,000 个实例)。这些随机数据点模拟在很长一段时间内,对于每个输入将看到的值。尽管听起来工作量很大,但这正是 Engage 和 Workspace 的亮点。一旦我们提交输入和模型,一切都会得到处理。
• 分析过程输出
有了模拟数据,您就可以使用传输方程来计算模拟结果。考虑到输入中的预期变异,通过模型运行足够多的模拟输入数据将可靠地指出该过程将在一段时间内输出的内容。
Monte Carlo 使用已知工程公式的4 个步骤
一家制造公司需要评估所提议产品的设计,这是一款每分钟必须泵送 12 毫升流体的小型活塞泵。考虑到活塞直径 (D)、冲程长度 (L) 和每分钟冲程数 (RPM) 的自然变异,您想要估计数千个泵的可能性能。理想情况下,数千个泵的泵流量将具有不大于 0.2 毫升的标准差。
• 确定传输方程
进行 Monte Carlo 模拟的第一步是确定传输方程。在本例中,您只需使用已知的工程公式来测量泵流量:
流量(以毫升为单位)= π(D/2)2 ∗ L ∗ RPM
• 定义输入参数
现在,必须定义传输方程中使用的每个输入的分布和参数。泵的活塞直径和冲程长度是已知的,但必须计算达到所需 12 毫升/分钟流速所需的每分钟冲程数 (RPM)。每个冲程泵送的体积按以下方程计算:π(D/2)2 * L
如果 D = 0.8,L = 2.5,则每个冲程排出 1.256 毫升流体。因此,要达到 12 毫升/分钟的流速,RPM 为 9.549。
根据贵厂制造的其他泵的性能,您可以假定活塞直径呈正态分布,均值为 0.8 厘米,标准差为 0.003 厘米。冲程长度呈正态分布,均值为 2.5 厘米,标准差为 0.15 厘米。最后,每分钟冲程数呈正态分布,均值为 9.549 RPM,标准差为 0.17 RPM。
• 在 Engage 或 Workspace 中设置模拟
单击顶部功能区中的插入选项卡,然后选择 Monte Carlo 模拟。
我们将它变得非常简单 — 您只需为每个变量提供名称,从下拉菜单中选择一个分布,然后输入参数。我们将按照上面所述的内容进行操作。如果您不确定数据遵循哪种分布,可以选择使用数据确定。这将提示您上传数据的 .csv 文件,可从以下几个选项中进行选择:
• 模拟和分析过程输出
下一步是给出方程。在这里,操作非常简单,只需为您的输出提供名称(我们提供的名称是 Flow),然后键入我们在上面确定的正确传输方程。您还可以添加规格上限和规格下限以查看模拟的比较情况。
然后,在功能区中,选择要运行的模拟数量(100,000 是不错的基准),然后单击用来运行模拟的按钮。
对于为了撰写本文而生成的随机数据,基于 100,000 个样本的平均流速为 11.996。从平均值来看,我们达到了目标,但最小值为 8.7817,最大值为 15.7057。这是一个相当大的范围。(所有组件的)传输变异导致标准差为 0.756 毫升,这远远超过目标值 0.2 毫升。
看起来这种泵的设计变异太大,需要在投入生产之前进一步完善。从这里,我们看到模拟所带来的好处。如果我们直接投入生产,很可能会生产出太多被退货的泵。借助 Monte Carlo 模拟,我们能够解决所有这些问题,而不会因制造和测试数千个原型或过早投入生产而产生费用。
您可能想了解这些模拟结果是否站得住脚,不妨自己尝试一下吧!运行不同的模拟将导致轻微的变化,但每次的最终结果(流速变异量不可接受)都会保持一致。这就是 Monte Carlo 方法的强大之处。
另一个可选步骤:参数优化
了解到标准差过高非常有价值,但 Engage 和 Workspace 真正突出的地方在于它们能够帮助改善状况。这就是参数优化的用武之地。
让我们看看第一个输入:活塞直径。平均值为 0.8,大部分数据将接近该值,或者在平均值的一两个标准差内。但是,如果活塞直径越小,流动效率越高,该怎么办?参数优化有助于我们回答这个问题。
为了进行参数优化,我们需要为每个输入指定搜索范围。在本例中,为简单起见,我指定的算法搜索范围是 +/- 3 个标准差。然后,Engage 或 Workspace 将帮助我们为每个输入找到要实现目标(在本例中是减小标准差)的最佳设置。选择合适的范围至关重要;确保您输入的整个范围都可以运行;如果找到的最佳解决方案无法在生产环境中复制,则毫无用处。
如果您在 Minitab Statistical Software 中用过响应优化器,则原理类似。下面是我们的结果:
基于以上结果,如果要减小标准差,则应当减小冲程长度和每分钟冲程数。活塞直径可以保持类似大小。请记住,Monte Carlo 模拟的关键之处在于,能够在不构建单个新原型或进行新试验的情况下找出所有这些结果。
Monte Carlo 使用试验设计 (DOE) 响应方程
如果您不知道要使用什么方程,或者您正在尝试模拟独特过程的结果,该怎么办?此时,我们可以将 Minitab Statistical Software 的设计试验功能与 Engage 或 Workspace 的模拟功能相结合。
一家电子制造商已指派您改进其电极清洁操作,该操作为电镀金属部件做准备。制造商通过电镀在原材料上涂上一层不同的金属,以实现所需的特性。电镀不会附着在肮脏的表面上,因此该公司有一个连接到自动电镀机的连续流电极清洗系统。传送带将每个部件浸入槽中,槽中的电压通过部件传送,从而对部件进行清洁。如果清洁不充分,会导致平均粗糙度的均方根(简称 RMS)值太高以及表面光洁度较差。经过正确清洁的部件具有光滑的表面和较低的 RMS。
为了优化该过程,可以调整两个关键输入:电压 (Vdc) 和电流密度 (ASF)。对于电极清洁方法,Vdc 的典型工程限值为 3 至 12 伏。电流密度限值为 10 至 150 安培/平方英尺 (ASF)。
• 确定传输方程
您不能针对该过程使用教材上的已知公式,但可以在 Minitab 中设置响应曲面 DOE 以确定传输方程。响应曲面 DOE 通常用于通过为“关键少数”可控因子寻找最佳设置来优化响应。
在本例中,响应将是部件在清洁后的表面质量。
要在 Minitab 中创建响应曲面试验,请选择统计 > DOE > 响应曲面 > 创建响应曲面设计。由于我们有两个因子(电压 (Vdc) 和电流密度 (ASF)),因此我们将选择试验次数为 13 的双因子中心复合设计。
Minitab 创建设计试验后,您需要执行 13 次试验、收集数据并记录 13 个清洁后部件的表面粗糙度。通过 Minitab,可轻松分析 DOE 结果、简化模型和使用残差图检查假定。使用最终模型和 Minitab 的响应优化器,可以找到变量的最佳设置。在本例中,您将电压设置为 7.74,将 ASF 设置为 77.8,所获得的粗糙度值为 39.4。
响应曲面 DOE 为 Monte Carlo 模拟生成以下传输方程:
粗糙度 = 957.8 − 189.4(Vdc) − 4.81(ASF) + 12.26(Vdc2) + 0.0309(ASF2)
• 定义输入参数
现在,您可以为Monte Carlo模拟输入设置参数定义,并将它们带入Engage或Workspace 中。
请注意,标准差必须已知或基于现有的过程知识进行估计。这适用于所有 Monte Carlo 输入。电压呈正态分布,均值为 7.74 Vdc,标准差为 0.14 Vdc。每平方英尺安培数 (ASF) 呈正态分布,均值为 77.8 ASF,标准差为 3 ASF。
• 在 Engage 或 Workspace 中设置模拟
这与步骤 3 完全相同。单击功能区中的插入 > Monte Carlo 模拟,添加您的输入并定义其参数,然后输入您的模型。在本例中,如果您拥有最新版本的 Minitab,则可以单击鼠标右键,然后点击发送到 Engage 或发送到 Minitab Workspace。如果您没有,则可以从 Minitab 输出中手动复制它并将其粘贴到 Engage 或 Workspace 的模型字段中。
• 模拟和分析过程输出
汇总表明,即使基础输入呈正态分布,RMS 粗糙度的分布也不是正态的。该汇总还显示所有组件的传输变异导致标准差为 0.521,根据您掌握的过程知识判断,这是不错的过程结果。基于试验次数仅为 13 的 DOE,我们可以确定在该过程中将看到的实际情况。同样,由于这基于模拟数据,您的答案会略有不同,但通常而言答案应该是正确的。如有必要,我们可以查看参数优化以微调我们的答案并找到最佳解决方案。 收起阅读 »
使用 Engage 或 Workspace 创建 Monte Carlo 模拟的 4 个简单步骤
20 世纪 40 年代,研究原子弹的科学家应用 Monte Carlo 模拟计算了一个裂变铀原子引起另一个裂变反应的概率,这是该模拟的首次应用,自此以来已经取得了很大进展。今天我们将介绍如何使用 Minitab 为已知的工程公式和 DOE 方程创建 Monte Carlo 模拟。
由于当时铀供应短缺,试验的试错空间很小,因此 Monte Carlo 模拟一直专注于根据模拟数据计算可靠的概率。如今,从材料工程到医疗设备包装密封再到炼钢,模拟数据经常用于许多场景,例如资源有限的场景,或者收集真实数据过于昂贵或不切实际的场景。使用 Engage 或 Workspace 的 Monte Carlo 模拟工具可以:
(1)模拟可能结果的范围以帮助做出决策。
(2)预测财务结果或估计项目时间表。
(3)了解过程或系统中的变异性。
(4)在过程或系统中发现问题。
(5)通过了解成本/效益关系来管理风险。
开始使用任何 Monte Carlo 模拟的 4 个步骤
模拟可能非常复杂,具体取决于所涉及因子的数量。但所有 Monte Carlo 模拟基本上都有四个简单的步骤:
1.确定传输方程
要创建 Monte Carlo 模拟,您需要一个包含要探索的业务活动、计划或过程的定量模型。过程的数学表达式称为“传输方程”。这可以是已知的工程或业务公式,也可以基于根据设计试验 (DOE) 或回归分析创建的模型。借助 Minitab Engage 和 Minitab Workspace 等软件,您能够创建复杂的方程,甚至是具有多个可能相互依赖的响应的方程。
2.定义输入参数
对于传输方程中的每个因子,确定其数据的分布方式。一些输入可能遵循正态分布,而另一些则遵循三角分布或均匀分布。然后,您需要确定每个输入的分布参数。例如,需要为遵循正态分布的输入指定均值和标准差。如果您不确定数据遵循哪种分布,可以使用 Engage 和 Workspace 提供的工具来确定。
3.设置模拟
要进行有效的模拟,您必须为每个输入创建一个非常大的随机数据集(大约包含 100,000 个实例)。这些随机数据点模拟在很长一段时间内,对于每个输入将看到的值。尽管听起来工作量很大,但这正是 Engage 和 Workspace 的亮点。一旦我们提交输入和模型,一切都会得到处理。
4.分析过程输出
有了模拟数据,您就可以使用传输方程来计算模拟结果。考虑到输入中的预期变异,通过模型运行足够多的模拟输入数据将可靠地指出该过程将在一段时间内输出的内容。
Monte Carlo 使用已知工程公式的 4 个步骤
一家制造公司需要评估所提议产品的设计,这是一款每分钟必须泵送 12 毫升流体的小型活塞泵。考虑到活塞直径 (D)、冲程长度 (L) 和每分钟冲程数 (RPM) 的自然变异,您想要估计数千个泵的可能性能。理想情况下,数千个泵的泵流量将具有不大于 0.2 毫升的标准差。
1.确定传输方程
进行 Monte Carlo 模拟的第一步是确定传输方程。在本例中,您只需使用已知的工程公式来测量泵流量:
流量(以毫升为单位)= π(D/2)2 ∗ L ∗ RPM
2.定义输入参数
现在,必须定义传输方程中使用的每个输入的分布和参数。泵的活塞直径和冲程长度是已知的,但必须计算达到所需 12 毫升/分钟流速所需的每分钟冲程数 (RPM)。每个冲程泵送的体积按以下方程计算:
π(D/2)2 * L
如果 D = 0.8,L = 2.5,则每个冲程排出 1.256 毫升流体。因此,要达到 12 毫升/分钟的流速,RPM 为 9.549。
根据贵厂制造的其他泵的性能,您可以假定活塞直径呈正态分布,均值为 0.8 厘米,标准差为 0.003 厘米。冲程长度呈正态分布,均值为 2.5 厘米,标准差为 0.15 厘米。最后,每分钟冲程数呈正态分布,均值为 9.549 RPM,标准差为 0.17 RPM。
3.在 Engage 或 Workspace 中设置模拟
单击顶部功能区中的插入选项卡,然后选择 Monte Carlo 模拟。
我们将它变得非常简单 — 您只需为每个变量提供名称,从下拉菜单中选择一个分布,然后输入参数。我们将按照上面所述的内容进行操作。如果您不确定数据遵循哪种分布,可以选择使用数据确定。这将提示您上传数据的 .csv 文件,可从以下几个选项中进行选择:
4.模拟和分析过程输出
下一步是给出方程。在这里,操作非常简单,只需为您的输出提供名称(我们提供的名称是 Flow),然后键入我们在上面确定的正确传输方程。您还可以添加规格上限和规格下限以查看模拟的比较情况。
然后,在功能区中,选择要运行的模拟数量(100,000 是不错的基准),然后单击用来运行模拟的按钮。
对于为了撰写本文而生成的随机数据,基于 100,000 个样本的平均流速为 11.996。从平均值来看,我们达到了目标,但最小值为 8.7817,最大值为 15.7057。这是一个相当大的范围。(所有组件的)传输变异导致标准差为 0.756 毫升,这远远超过目标值 0.2 毫升。
看起来这种泵的设计变异太大,需要在投入生产之前进一步完善。从这里,我们看到模拟所带来的好处。如果我们直接投入生产,很可能会生产出太多被退货的泵。借助 Monte Carlo 模拟,我们能够解决所有这些问题,而不会因制造和测试数千个原型或过早投入生产而产生费用。
您可能想了解这些模拟结果是否站得住脚,不妨自己尝试一下吧!运行不同的模拟将导致轻微的变化,但每次的最终结果(流速变异量不可接受)都会保持一致。这就是 Monte Carlo 方法的强大之处。
另一个可选步骤:参数优化
了解到标准差过高非常有价值,但 Engage 和 Workspace 真正突出的地方在于它们能够帮助改善状况。这就是参数优化的用武之地。
让我们看看第一个输入:活塞直径。平均值为 0.8,大部分数据将接近该值,或者在平均值的一两个标准差内。但是,如果活塞直径越小,流动效率越高,该怎么办?参数优化有助于我们回答这个问题。
为了进行参数优化,我们需要为每个输入指定搜索范围。在本例中,为简单起见,我指定的算法搜索范围是 +/- 3 个标准差。然后,Engage 或 Workspace 将帮助我们为每个输入找到要实现目标(在本例中是减小标准差)的最佳设置。选择合适的范围至关重要;确保您输入的整个范围都可以运行;如果找到的最佳解决方案无法在生产环境中复制,则毫无用处。
如果您在 Minitab Statistical Software 中用过响应优化器,则原理类似。下面是我们的结果:
基于以上结果,如果要减小标准差,则应当减小冲程长度和每分钟冲程数。活塞直径可以保持类似大小。请记住,Monte Carlo 模拟的关键之处在于,能够在不构建单个新原型或进行新试验的情况下找出所有这些结果。
Monte Carlo 使用试验设计 (DOE) 响应方程
如果您不知道要使用什么方程,或者您正在尝试模拟独特过程的结果,该怎么办?此时,我们可以将 Minitab Statistical Software 的设计试验功能与 Engage 或 Workspace 的模拟功能相结合。
一家电子制造商已指派您改进其电极清洁操作,该操作为电镀金属部件做准备。制造商通过电镀在原材料上涂上一层不同的金属,以实现所需的特性。电镀不会附着在肮脏的表面上,因此该公司有一个连接到自动电镀机的连续流电极清洗系统。传送带将每个部件浸入槽中,槽中的电压通过部件传送,从而对部件进行清洁。如果清洁不充分,会导致平均粗糙度的均方根(简称 RMS)值太高以及表面光洁度较差。经过正确清洁的部件具有光滑的表面和较低的 RMS。
为了优化该过程,可以调整两个关键输入:电压 (Vdc) 和电流密度 (ASF)。对于电极清洁方法,Vdc 的典型工程限值为 3 至 12 伏。电流密度限值为 10 至 150 安培/平方英尺 (ASF)。
1.确定传输方程
您不能针对该过程使用教材上的已知公式,但可以在 Minitab 中设置响应曲面 DOE 以确定传输方程。响应曲面 DOE 通常用于通过为“关键少数”可控因子寻找最佳设置来优化响应。
在本例中,响应将是部件在清洁后的表面质量。
要在 Minitab 中创建响应曲面试验,请选择统计 > DOE > 响应曲面 > 创建响应曲面设计。由于我们有两个因子(电压 (Vdc) 和电流密度 (ASF)),因此我们将选择试验次数为 13 的双因子中心复合设计。
Minitab 创建设计试验后,您需要执行 13 次试验、收集数据并记录 13 个清洁后部件的表面粗糙度。通过 Minitab,可轻松分析 DOE 结果、简化模型和使用残差图检查假定。使用最终模型和 Minitab 的响应优化器,可以找到变量的最佳设置。在本例中,您将电压设置为 7.74,将 ASF 设置为 77.8,所获得的粗糙度值为 39.4。
响应曲面 DOE 为 Monte Carlo 模拟生成以下传输方程:
粗糙度 = 957.8 − 189.4(Vdc) − 4.81(ASF) + 12.26(Vdc2) + 0.0309(ASF2)
2.定义输入参数
现在,您可以为 Monte Carlo 模拟输入设置参数定义,并将它们带入 Engage 或 Workspace 中。
请注意,标准差必须已知或基于现有的过程知识进行估计。这适用于所有 Monte Carlo 输入。电压呈正态分布,均值为 7.74 Vdc,标准差为 0.14 Vdc。每平方英尺安培数 (ASF) 呈正态分布,均值为 77.8 ASF,标准差为 3 ASF。
3.在 Engage 或 Workspace 中设置模拟
这与步骤 3 完全相同。单击功能区中的插入 > Monte Carlo 模拟,添加您的输入并定义其参数,然后输入您的模型。在本例中,如果您拥有最新版本的 Minitab,则可以单击鼠标右键,然后点击发送到 Engage 或发送到 Minitab Workspace。如果您没有,则可以从 Minitab 输出中手动复制它并将其粘贴到 Engage 或 Workspace 的模型字段中。
4.模拟和分析过程输出
汇总表明,即使基础输入呈正态分布,RMS 粗糙度的分布也不是正态的。该汇总还显示所有组件的传输变异导致标准差为 0.521,根据您掌握的过程知识判断,这是不错的过程结果。基于试验次数仅为 13 的 DOE,我们可以确定在该过程中将看到的实际情况。同样,由于这基于模拟数据,您的答案会略有不同,但通常而言答案应该是正确的。如有必要,我们可以查看参数优化以微调我们的答案并找到最佳解决方案。
本文最初出现在Minitab博客上。 收起阅读 »
由于当时铀供应短缺,试验的试错空间很小,因此 Monte Carlo 模拟一直专注于根据模拟数据计算可靠的概率。如今,从材料工程到医疗设备包装密封再到炼钢,模拟数据经常用于许多场景,例如资源有限的场景,或者收集真实数据过于昂贵或不切实际的场景。使用 Engage 或 Workspace 的 Monte Carlo 模拟工具可以:
(1)模拟可能结果的范围以帮助做出决策。
(2)预测财务结果或估计项目时间表。
(3)了解过程或系统中的变异性。
(4)在过程或系统中发现问题。
(5)通过了解成本/效益关系来管理风险。
开始使用任何 Monte Carlo 模拟的 4 个步骤
模拟可能非常复杂,具体取决于所涉及因子的数量。但所有 Monte Carlo 模拟基本上都有四个简单的步骤:
1.确定传输方程
要创建 Monte Carlo 模拟,您需要一个包含要探索的业务活动、计划或过程的定量模型。过程的数学表达式称为“传输方程”。这可以是已知的工程或业务公式,也可以基于根据设计试验 (DOE) 或回归分析创建的模型。借助 Minitab Engage 和 Minitab Workspace 等软件,您能够创建复杂的方程,甚至是具有多个可能相互依赖的响应的方程。
2.定义输入参数
对于传输方程中的每个因子,确定其数据的分布方式。一些输入可能遵循正态分布,而另一些则遵循三角分布或均匀分布。然后,您需要确定每个输入的分布参数。例如,需要为遵循正态分布的输入指定均值和标准差。如果您不确定数据遵循哪种分布,可以使用 Engage 和 Workspace 提供的工具来确定。
3.设置模拟
要进行有效的模拟,您必须为每个输入创建一个非常大的随机数据集(大约包含 100,000 个实例)。这些随机数据点模拟在很长一段时间内,对于每个输入将看到的值。尽管听起来工作量很大,但这正是 Engage 和 Workspace 的亮点。一旦我们提交输入和模型,一切都会得到处理。
4.分析过程输出
有了模拟数据,您就可以使用传输方程来计算模拟结果。考虑到输入中的预期变异,通过模型运行足够多的模拟输入数据将可靠地指出该过程将在一段时间内输出的内容。
Monte Carlo 使用已知工程公式的 4 个步骤
一家制造公司需要评估所提议产品的设计,这是一款每分钟必须泵送 12 毫升流体的小型活塞泵。考虑到活塞直径 (D)、冲程长度 (L) 和每分钟冲程数 (RPM) 的自然变异,您想要估计数千个泵的可能性能。理想情况下,数千个泵的泵流量将具有不大于 0.2 毫升的标准差。
1.确定传输方程
进行 Monte Carlo 模拟的第一步是确定传输方程。在本例中,您只需使用已知的工程公式来测量泵流量:
流量(以毫升为单位)= π(D/2)2 ∗ L ∗ RPM
2.定义输入参数
现在,必须定义传输方程中使用的每个输入的分布和参数。泵的活塞直径和冲程长度是已知的,但必须计算达到所需 12 毫升/分钟流速所需的每分钟冲程数 (RPM)。每个冲程泵送的体积按以下方程计算:
π(D/2)2 * L
如果 D = 0.8,L = 2.5,则每个冲程排出 1.256 毫升流体。因此,要达到 12 毫升/分钟的流速,RPM 为 9.549。
根据贵厂制造的其他泵的性能,您可以假定活塞直径呈正态分布,均值为 0.8 厘米,标准差为 0.003 厘米。冲程长度呈正态分布,均值为 2.5 厘米,标准差为 0.15 厘米。最后,每分钟冲程数呈正态分布,均值为 9.549 RPM,标准差为 0.17 RPM。
3.在 Engage 或 Workspace 中设置模拟
单击顶部功能区中的插入选项卡,然后选择 Monte Carlo 模拟。
我们将它变得非常简单 — 您只需为每个变量提供名称,从下拉菜单中选择一个分布,然后输入参数。我们将按照上面所述的内容进行操作。如果您不确定数据遵循哪种分布,可以选择使用数据确定。这将提示您上传数据的 .csv 文件,可从以下几个选项中进行选择:
4.模拟和分析过程输出
下一步是给出方程。在这里,操作非常简单,只需为您的输出提供名称(我们提供的名称是 Flow),然后键入我们在上面确定的正确传输方程。您还可以添加规格上限和规格下限以查看模拟的比较情况。
然后,在功能区中,选择要运行的模拟数量(100,000 是不错的基准),然后单击用来运行模拟的按钮。
对于为了撰写本文而生成的随机数据,基于 100,000 个样本的平均流速为 11.996。从平均值来看,我们达到了目标,但最小值为 8.7817,最大值为 15.7057。这是一个相当大的范围。(所有组件的)传输变异导致标准差为 0.756 毫升,这远远超过目标值 0.2 毫升。
看起来这种泵的设计变异太大,需要在投入生产之前进一步完善。从这里,我们看到模拟所带来的好处。如果我们直接投入生产,很可能会生产出太多被退货的泵。借助 Monte Carlo 模拟,我们能够解决所有这些问题,而不会因制造和测试数千个原型或过早投入生产而产生费用。
您可能想了解这些模拟结果是否站得住脚,不妨自己尝试一下吧!运行不同的模拟将导致轻微的变化,但每次的最终结果(流速变异量不可接受)都会保持一致。这就是 Monte Carlo 方法的强大之处。
另一个可选步骤:参数优化
了解到标准差过高非常有价值,但 Engage 和 Workspace 真正突出的地方在于它们能够帮助改善状况。这就是参数优化的用武之地。
让我们看看第一个输入:活塞直径。平均值为 0.8,大部分数据将接近该值,或者在平均值的一两个标准差内。但是,如果活塞直径越小,流动效率越高,该怎么办?参数优化有助于我们回答这个问题。
为了进行参数优化,我们需要为每个输入指定搜索范围。在本例中,为简单起见,我指定的算法搜索范围是 +/- 3 个标准差。然后,Engage 或 Workspace 将帮助我们为每个输入找到要实现目标(在本例中是减小标准差)的最佳设置。选择合适的范围至关重要;确保您输入的整个范围都可以运行;如果找到的最佳解决方案无法在生产环境中复制,则毫无用处。
如果您在 Minitab Statistical Software 中用过响应优化器,则原理类似。下面是我们的结果:
基于以上结果,如果要减小标准差,则应当减小冲程长度和每分钟冲程数。活塞直径可以保持类似大小。请记住,Monte Carlo 模拟的关键之处在于,能够在不构建单个新原型或进行新试验的情况下找出所有这些结果。
Monte Carlo 使用试验设计 (DOE) 响应方程
如果您不知道要使用什么方程,或者您正在尝试模拟独特过程的结果,该怎么办?此时,我们可以将 Minitab Statistical Software 的设计试验功能与 Engage 或 Workspace 的模拟功能相结合。
一家电子制造商已指派您改进其电极清洁操作,该操作为电镀金属部件做准备。制造商通过电镀在原材料上涂上一层不同的金属,以实现所需的特性。电镀不会附着在肮脏的表面上,因此该公司有一个连接到自动电镀机的连续流电极清洗系统。传送带将每个部件浸入槽中,槽中的电压通过部件传送,从而对部件进行清洁。如果清洁不充分,会导致平均粗糙度的均方根(简称 RMS)值太高以及表面光洁度较差。经过正确清洁的部件具有光滑的表面和较低的 RMS。
为了优化该过程,可以调整两个关键输入:电压 (Vdc) 和电流密度 (ASF)。对于电极清洁方法,Vdc 的典型工程限值为 3 至 12 伏。电流密度限值为 10 至 150 安培/平方英尺 (ASF)。
1.确定传输方程
您不能针对该过程使用教材上的已知公式,但可以在 Minitab 中设置响应曲面 DOE 以确定传输方程。响应曲面 DOE 通常用于通过为“关键少数”可控因子寻找最佳设置来优化响应。
在本例中,响应将是部件在清洁后的表面质量。
要在 Minitab 中创建响应曲面试验,请选择统计 > DOE > 响应曲面 > 创建响应曲面设计。由于我们有两个因子(电压 (Vdc) 和电流密度 (ASF)),因此我们将选择试验次数为 13 的双因子中心复合设计。
Minitab 创建设计试验后,您需要执行 13 次试验、收集数据并记录 13 个清洁后部件的表面粗糙度。通过 Minitab,可轻松分析 DOE 结果、简化模型和使用残差图检查假定。使用最终模型和 Minitab 的响应优化器,可以找到变量的最佳设置。在本例中,您将电压设置为 7.74,将 ASF 设置为 77.8,所获得的粗糙度值为 39.4。
响应曲面 DOE 为 Monte Carlo 模拟生成以下传输方程:
粗糙度 = 957.8 − 189.4(Vdc) − 4.81(ASF) + 12.26(Vdc2) + 0.0309(ASF2)
2.定义输入参数
现在,您可以为 Monte Carlo 模拟输入设置参数定义,并将它们带入 Engage 或 Workspace 中。
请注意,标准差必须已知或基于现有的过程知识进行估计。这适用于所有 Monte Carlo 输入。电压呈正态分布,均值为 7.74 Vdc,标准差为 0.14 Vdc。每平方英尺安培数 (ASF) 呈正态分布,均值为 77.8 ASF,标准差为 3 ASF。
3.在 Engage 或 Workspace 中设置模拟
这与步骤 3 完全相同。单击功能区中的插入 > Monte Carlo 模拟,添加您的输入并定义其参数,然后输入您的模型。在本例中,如果您拥有最新版本的 Minitab,则可以单击鼠标右键,然后点击发送到 Engage 或发送到 Minitab Workspace。如果您没有,则可以从 Minitab 输出中手动复制它并将其粘贴到 Engage 或 Workspace 的模型字段中。
4.模拟和分析过程输出
汇总表明,即使基础输入呈正态分布,RMS 粗糙度的分布也不是正态的。该汇总还显示所有组件的传输变异导致标准差为 0.521,根据您掌握的过程知识判断,这是不错的过程结果。基于试验次数仅为 13 的 DOE,我们可以确定在该过程中将看到的实际情况。同样,由于这基于模拟数据,您的答案会略有不同,但通常而言答案应该是正确的。如有必要,我们可以查看参数优化以微调我们的答案并找到最佳解决方案。
本文最初出现在Minitab博客上。 收起阅读 »
等价检验 VS 显著性检验
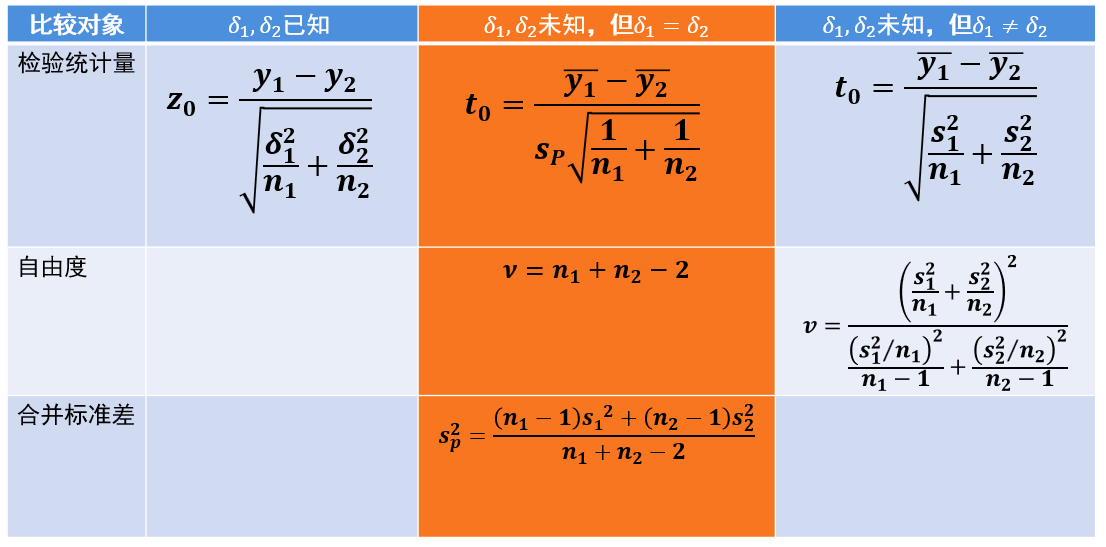
传统显著性检验用于推断样本所代表的总体均值是否相等,它的检验假设为样本来自同一总体(即总体均值相等)。在应用中,显著性检验结果不能评价差别的大小,也不能说明差别是否有实际意义,所谓差别显著是指在统计学理论上认为样本来自不同的总体。另外显著性检验在均值差异性比较中也存在一定的局限性,下面我们以双样本t检验为例来说明。
显著性检验的局限性
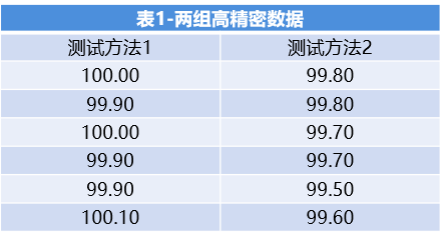
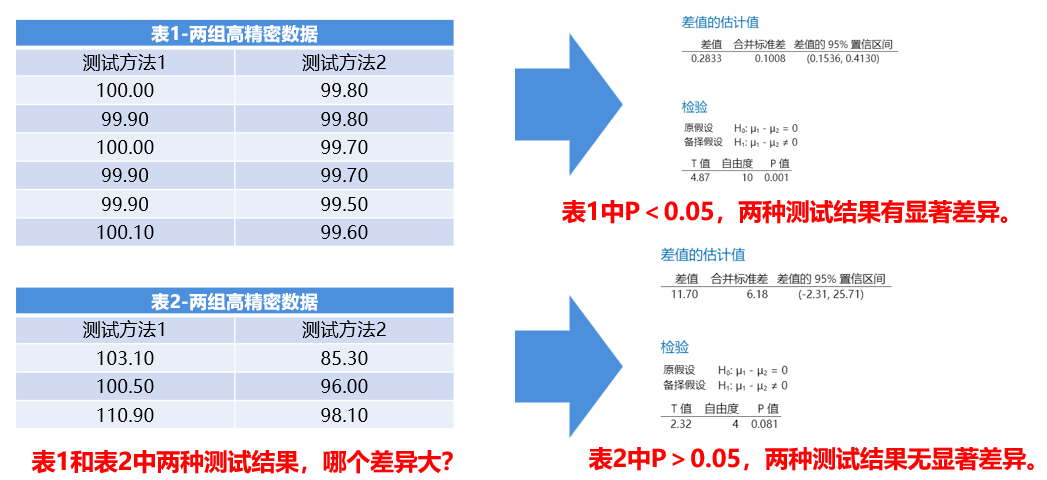
我们看到下表1中两种测试方法得到的数据,希望比较两种测试方法得到的结果是否一致(等效)。
可能首先想到的方法就是用双样本t检验,我们来试试看(前提条件验证略)。
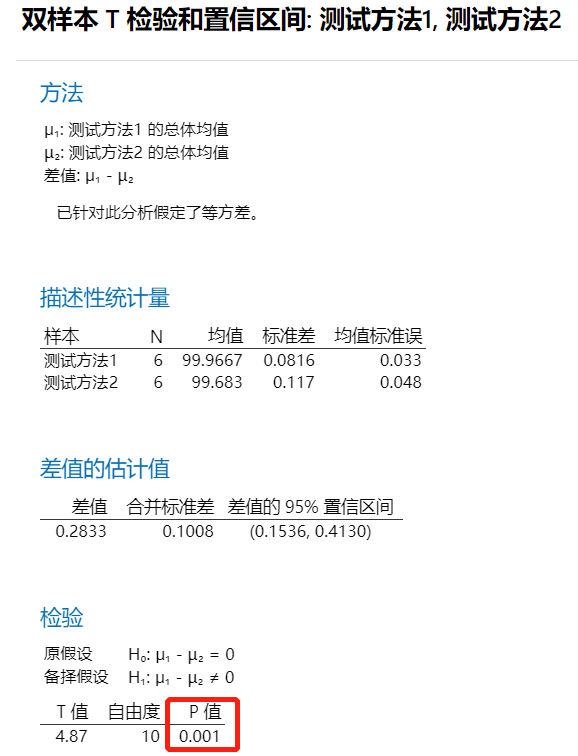
双样本t检验的结果显示,P=0.001<0.05,所以我们得到的结论是:两种测试方法的结果是有显著性差异的。拒绝是有说服力的,所以我们也不用担心犯第二类错误。
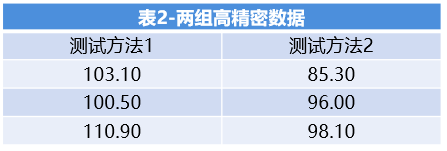
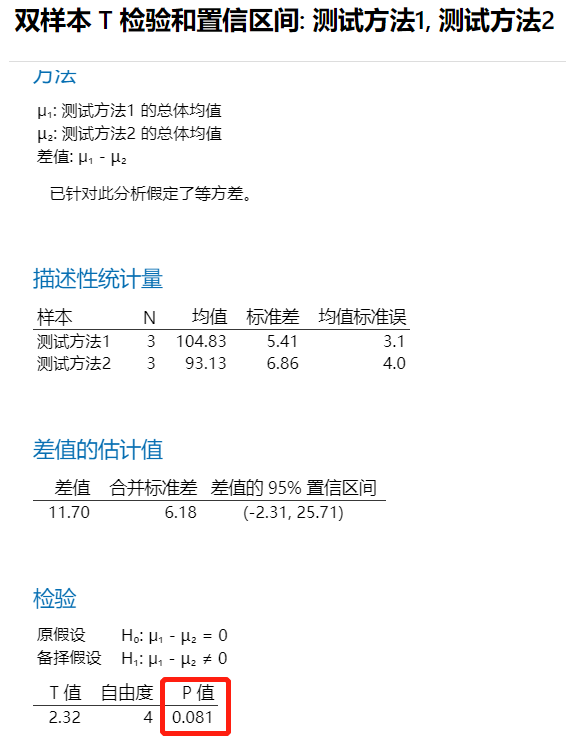
现在我们再来看看下表2中两种测试方法的数据,也想来比较有没有显著性差异。
同理,我们也来执行双样本t检验(前提条件验证略),得到如下结果。
双样本t检验的结果显示,P=0.081>0.05,所以我们得到的结论是:两种测试方法的结果无显著性差异的,即不拒绝原假设。不拒绝是没有说服力的,可能是样本量不够导致的(建议做功效与样本量的计算)。
基于以上分析,总结如下:
但是,如果你仔细去看一看表1和表2中的数据,有没有发现表1中两种测试方法结果差异比较小(但双样本t检验结果P=0.001<0.05),表2中两种测试方法结果差异比较大(但双样本t检验结果P=0.081>0.05),注意,这不是错觉,这是t检验本身存在的局限性。
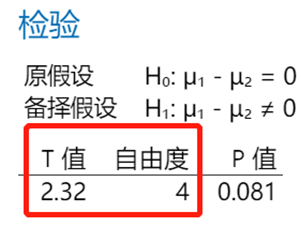
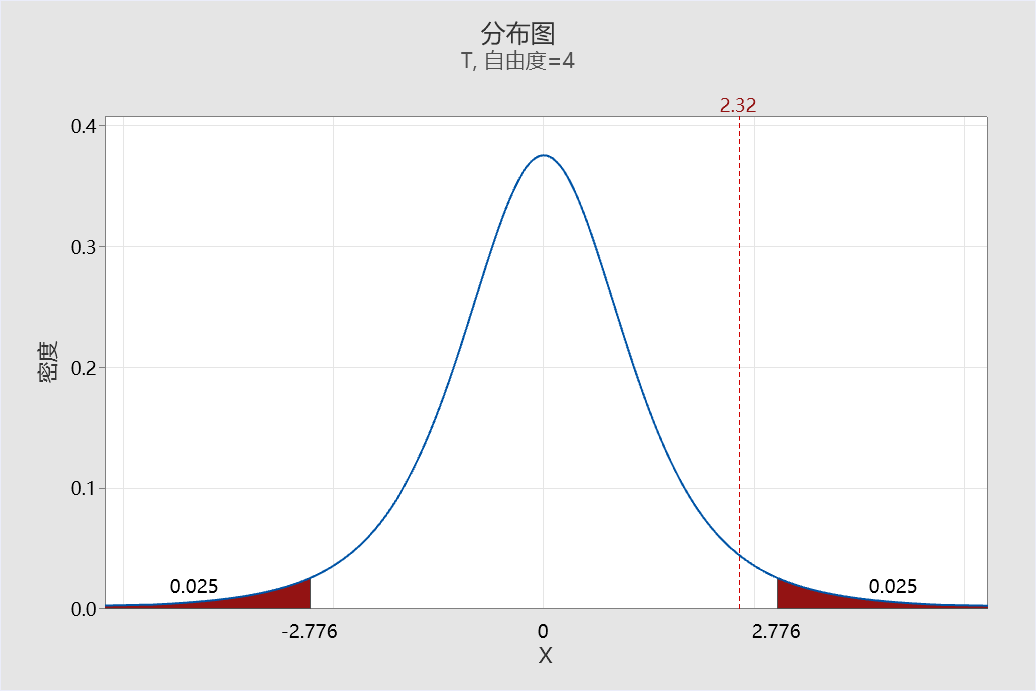
为什么这么说,我们以表2中数据(两总体标准差未知但相等)为例来看看t检验的基本原理。
T=2.32小于拒绝域临界值2.776,及检验统计量T落在非拒绝域(白色区域),故不拒绝原假设。换句话说,如果想拒绝原假设(得到两种测试方法有显著差异的结论),就需要检验统计量T值(绝对值)足够大,大到超过2.776,那么怎么做才能实现呢?通过后台公式我们能发现只需要:样本量足够大且/或合并标准差SP足够小。
其实这是一个有悖逻辑的发现,因为如果真的如此的话,那我以后直接选择摆烂不就可以吗(样本量少抽一点,测量变异搞大点,这样越不容易得到有显著差异)。
等价检验
从功能和实用意义上来讲,产品之间存在微小差异并不总是十分重要。例如,在200 mg的药物剂量中,相差1mg不会产生任何实际效应,那如果我想证明药物剂量不同对疗效是相同的或相近的,又该如何去验证呢?可不可以用显著性检验的方法(如t检验)?
显著性检验确定备择假设的方法是“想证明什么结论就把它放在备择假设上”,那能否把相等的结论放在备择假设上,如H0:μ≠μ0, H1: μ=μ0很遗憾,统计学中不可能处理这种“原假设是某个范围,而备择假设只是一个单点”的情况,只能处理备择假设为
H1:|μ-μ0|<△
H1: μ1<μ<μ2
其中μ1=μ0-△,μ2=μ0+△
这类检验问题称为等价检验(equivalence test)问题,也称等效性检验问题。其中(μ1,μ2)称为等价区间。它的原假设和备择假设为:
H0:μ<μ1或μ>μ2 H1:μ1≤μ≤μ2
等价检验实际上是双单侧假设检验(TOST),当左右两边的原假设同时被拒绝时才能认为原假设不成立。
等价检验 VS 显著性检验
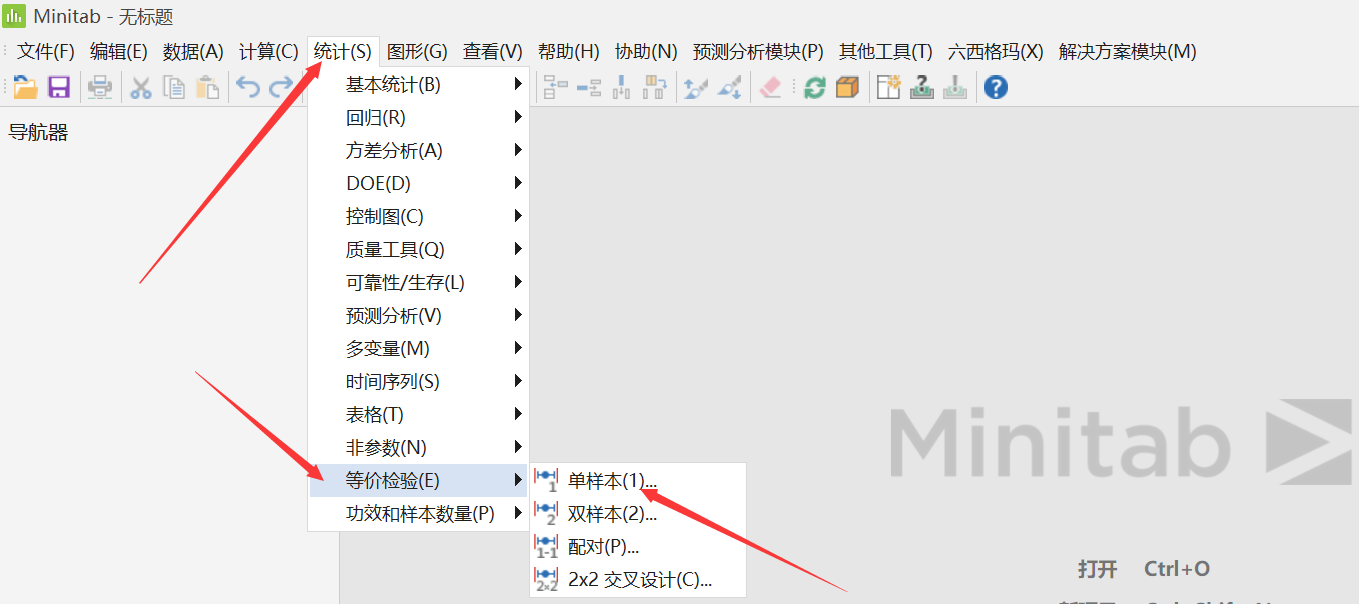
等价检验与显著性检验比较如上图,下面我们通过一个具体案例来说明一下(案例来自于蓝皮书第三版P161)。
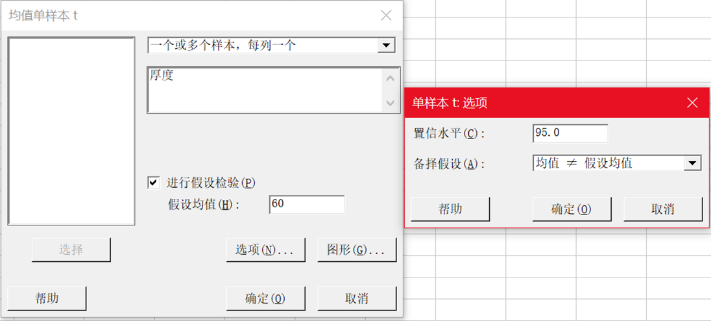
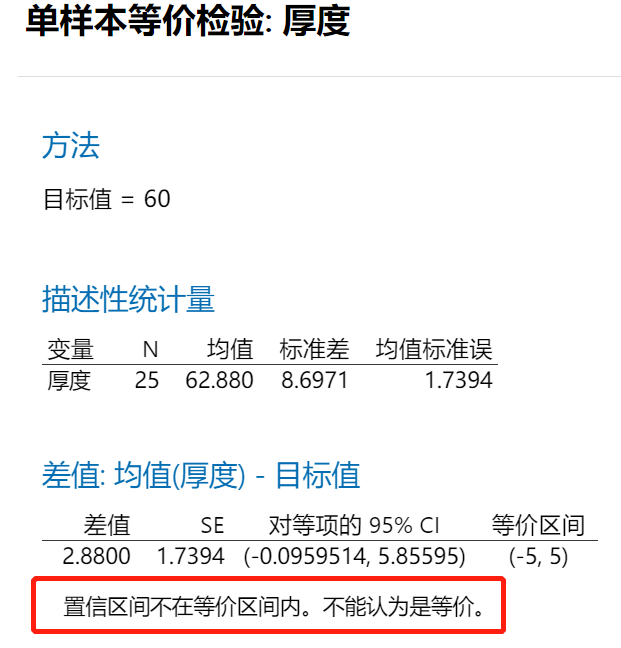
示例:在焊接电路板的过程中,焊锡膏的涂抹厚度是关键的控制量之一。工艺标准要求涂抹厚度的均值是60微米,均值偏差在5微米内。现在收集了25个焊点上的焊锡膏涂抹厚度。我们希望验证,涂抹厚度均值是60微米吗?涂抹厚度均值是落在(55,65)之内吗?
我们先来看看如果是用显著性检验(单样本t检验)会得到什么结果。
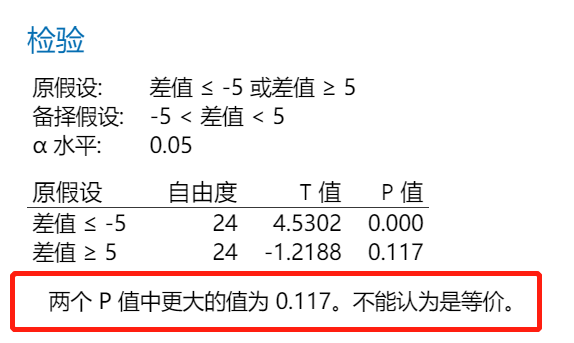
由于P值为0.111,因此无法拒绝原假设,也就是说没有充分的理由否认焊锡膏涂抹厚度均值为60。但“不否认”还不是明确的说明“均值就是60微米”的有说服力的结论。如果需要进一步确定“均值就是60微米”,或者更进一步判断其均值是否落入(55,65),则只能使用单样本等价检验方法(注意:即使是等价检验对于备择假设只是一个单点也是无能为力的)。
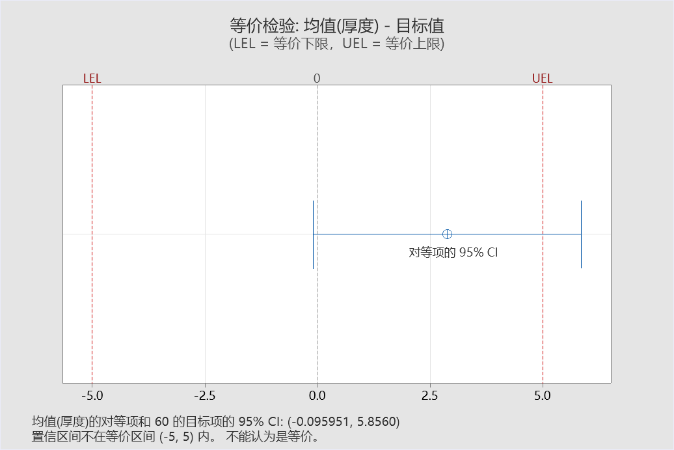
正如Minitab告诉你的,不能认为是等价的,即焊锡膏涂抹厚度均值可以认为是60微米,但未落在(55,65)之内,即精确度未达到误差小于5微米的水平。
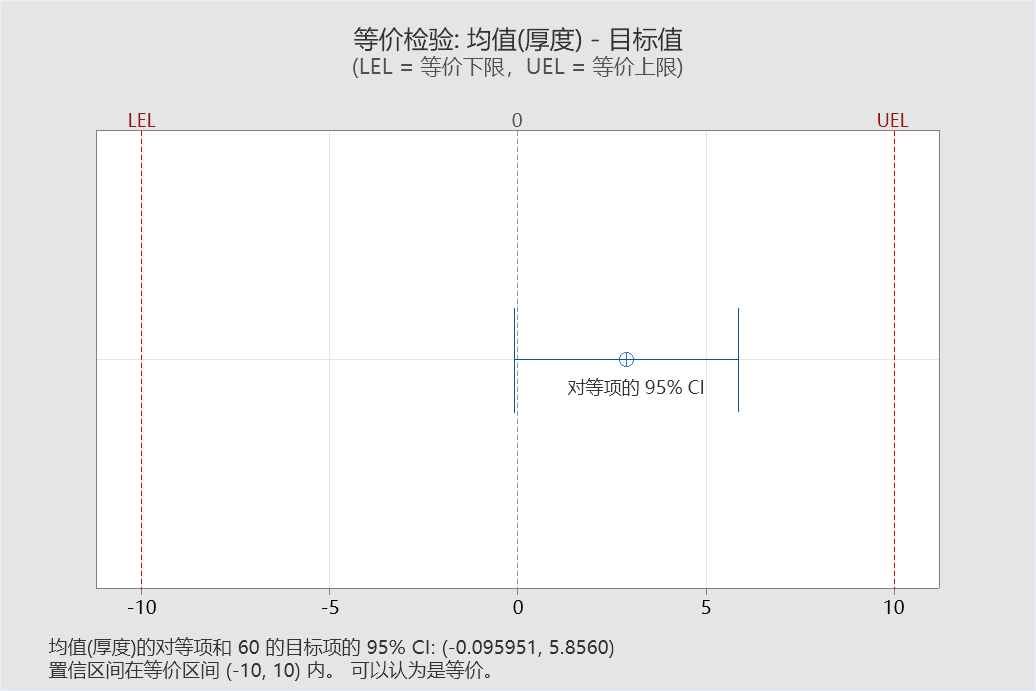
那如果允许误差放大些,比如说(50,70),结果就可以认为是等价的了。
请注意,我在这里不得不说明一下,千万不要说为了得到等价的结论而去改等价区间,我在这里修改只是为了说明问题,我们在实际工作一定是要事先指定好等价区间范围(防止扯皮)。
小结
要在等价检验和标准t检验之间进行选择,请考虑您希望证明或说明的内容。如果您希望证明两个均值相等或者证明均值等于目标值,而且您可以确切地定义在所属领域中属于重要差值的差值大小,则您可能希望使用等价检验,而不是标准t检验。 收起阅读 »
显著性检验的局限性
我们看到下表1中两种测试方法得到的数据,希望比较两种测试方法得到的结果是否一致(等效)。
可能首先想到的方法就是用双样本t检验,我们来试试看(前提条件验证略)。
双样本t检验的结果显示,P=0.001<0.05,所以我们得到的结论是:两种测试方法的结果是有显著性差异的。拒绝是有说服力的,所以我们也不用担心犯第二类错误。
现在我们再来看看下表2中两种测试方法的数据,也想来比较有没有显著性差异。
同理,我们也来执行双样本t检验(前提条件验证略),得到如下结果。
双样本t检验的结果显示,P=0.081>0.05,所以我们得到的结论是:两种测试方法的结果无显著性差异的,即不拒绝原假设。不拒绝是没有说服力的,可能是样本量不够导致的(建议做功效与样本量的计算)。
基于以上分析,总结如下:
但是,如果你仔细去看一看表1和表2中的数据,有没有发现表1中两种测试方法结果差异比较小(但双样本t检验结果P=0.001<0.05),表2中两种测试方法结果差异比较大(但双样本t检验结果P=0.081>0.05),注意,这不是错觉,这是t检验本身存在的局限性。
为什么这么说,我们以表2中数据(两总体标准差未知但相等)为例来看看t检验的基本原理。
T=2.32小于拒绝域临界值2.776,及检验统计量T落在非拒绝域(白色区域),故不拒绝原假设。换句话说,如果想拒绝原假设(得到两种测试方法有显著差异的结论),就需要检验统计量T值(绝对值)足够大,大到超过2.776,那么怎么做才能实现呢?通过后台公式我们能发现只需要:样本量足够大且/或合并标准差SP足够小。
其实这是一个有悖逻辑的发现,因为如果真的如此的话,那我以后直接选择摆烂不就可以吗(样本量少抽一点,测量变异搞大点,这样越不容易得到有显著差异)。
等价检验
从功能和实用意义上来讲,产品之间存在微小差异并不总是十分重要。例如,在200 mg的药物剂量中,相差1mg不会产生任何实际效应,那如果我想证明药物剂量不同对疗效是相同的或相近的,又该如何去验证呢?可不可以用显著性检验的方法(如t检验)?
显著性检验确定备择假设的方法是“想证明什么结论就把它放在备择假设上”,那能否把相等的结论放在备择假设上,如H0:μ≠μ0, H1: μ=μ0很遗憾,统计学中不可能处理这种“原假设是某个范围,而备择假设只是一个单点”的情况,只能处理备择假设为
H1:|μ-μ0|<△
H1: μ1<μ<μ2
其中μ1=μ0-△,μ2=μ0+△
这类检验问题称为等价检验(equivalence test)问题,也称等效性检验问题。其中(μ1,μ2)称为等价区间。它的原假设和备择假设为:
H0:μ<μ1或μ>μ2 H1:μ1≤μ≤μ2
等价检验实际上是双单侧假设检验(TOST),当左右两边的原假设同时被拒绝时才能认为原假设不成立。
等价检验 VS 显著性检验
等价检验与显著性检验比较如上图,下面我们通过一个具体案例来说明一下(案例来自于蓝皮书第三版P161)。
示例:在焊接电路板的过程中,焊锡膏的涂抹厚度是关键的控制量之一。工艺标准要求涂抹厚度的均值是60微米,均值偏差在5微米内。现在收集了25个焊点上的焊锡膏涂抹厚度。我们希望验证,涂抹厚度均值是60微米吗?涂抹厚度均值是落在(55,65)之内吗?
我们先来看看如果是用显著性检验(单样本t检验)会得到什么结果。
由于P值为0.111,因此无法拒绝原假设,也就是说没有充分的理由否认焊锡膏涂抹厚度均值为60。但“不否认”还不是明确的说明“均值就是60微米”的有说服力的结论。如果需要进一步确定“均值就是60微米”,或者更进一步判断其均值是否落入(55,65),则只能使用单样本等价检验方法(注意:即使是等价检验对于备择假设只是一个单点也是无能为力的)。
正如Minitab告诉你的,不能认为是等价的,即焊锡膏涂抹厚度均值可以认为是60微米,但未落在(55,65)之内,即精确度未达到误差小于5微米的水平。
那如果允许误差放大些,比如说(50,70),结果就可以认为是等价的了。
请注意,我在这里不得不说明一下,千万不要说为了得到等价的结论而去改等价区间,我在这里修改只是为了说明问题,我们在实际工作一定是要事先指定好等价区间范围(防止扯皮)。
小结
要在等价检验和标准t检验之间进行选择,请考虑您希望证明或说明的内容。如果您希望证明两个均值相等或者证明均值等于目标值,而且您可以确切地定义在所属领域中属于重要差值的差值大小,则您可能希望使用等价检验,而不是标准t检验。 收起阅读 »
防止缺货和优化库存水平的三个步骤
和大多数的问题解决方法一样,优化库存需要一个考虑周全的过程和几个步骤。当然,防止缺货的最简便方法是手头始终具有大量库存。然而,不优化库存也会产生难以预料的后果。过度生产和保持过高的库存水平可能会导致产品变质甚至腐坏。库存过剩不仅会在当下产生成本,而且当您需要生产更多商品来替换货架上放置时间过长的产品时,还会在以后产生隐性成本。
可通过多种方法来计算优化(将在下面解释),但优化库存的关键在于三个主要步骤:对影响库存的因素进行头脑风暴分析、收集数据并分析数据。在深入研究每个步骤之前,我们先来介绍一些有关缺货的基本知识。
什么是缺货?是什么原因造成的?
简单地说,缺货意味着由于产品不在库存中而无法履行或交付。这可能是因为产品需求量高于预期,或者因库存水平太低而无法满足当前需求。
缺货是否对企业不利?
用一个字概括,是。我们都属于各种各样的客户,当所需的产品或服务不可用时,我们都会有不好的感觉。这不仅会损害当前客户体验,而且会对您的品牌和客户关系产生长期影响。
因此...如何减少缺货?防止缺货的三个步骤如下
对影响缺货的因素(包括库存水平)进行头脑风暴分
防止缺货的最大因素是现有的库存水平。如果库存中没有足够的产品,将面临缺货。但现有库存只是一个因素。您还需要了解影响移动供应链的所有因素(如在途库存、销售额预测、历史销售业绩),甚至还需要了解您自己的供应商所带来的影响。
因此,如何保持库存水平足够高以满足客户需求,但又足够低以避免库存过剩?您需要对影响库存水平的因素进行头脑风暴分析。使用结构化的问题解决工具(如 CT 树或鱼骨图)可以让您获得成功。
下面是一个头脑风暴工具示例,该示例使用 Minitab Workspace 中的鱼骨图。
收集数据
一旦确定了影响缺货的关键因素,就需要收集有关这些因素的数据。请注意,可能需要从多个来源和系统收集库存数据,而且数据的请求和准备过程可能需要一些时间。考虑需要收集的数据量。
例如,考虑到一段时间发生的所有变化,若追溯到 5 年前可能太久了。收集几个月的数据可能更合理,所以请根据您的最佳判断来捕获您的过程的代表性快照。您可以请 IT 部门协助,或利用功能强大的数据统一工具(如 Minitab Connect)访问、集成和准备要分析的数据。
使用预测分析来分析数据
收集到数据之后,就可以开始进行最有趣的部分:分析!传统的业务分析和可视化技术在这方面可能存在不足,因为最有可能出现的直观效果是:现有库存越低,缺货量越大!由于我们已经知道这一点,因此我们真正想要确定的是:是否还有另一个重要因素是缺货的关键驱动因素?是否存在一个最佳库存水平既可最大限度地减少缺货,又不会造成积压和生产过剩?
因此,为什么要进行预测分析?简言之,设想创建一个方程,该方程将所有影响缺货的因素作为预测变量,并将缺货作为响应。就像高中代数一样,这些不同的因素有不同的权重,因此对结果的影响程度也不同。在 Minitab,我们开发了解决方案来专门帮助您解决这些问题! 收起阅读 »
可通过多种方法来计算优化(将在下面解释),但优化库存的关键在于三个主要步骤:对影响库存的因素进行头脑风暴分析、收集数据并分析数据。在深入研究每个步骤之前,我们先来介绍一些有关缺货的基本知识。
什么是缺货?是什么原因造成的?
简单地说,缺货意味着由于产品不在库存中而无法履行或交付。这可能是因为产品需求量高于预期,或者因库存水平太低而无法满足当前需求。
缺货是否对企业不利?
用一个字概括,是。我们都属于各种各样的客户,当所需的产品或服务不可用时,我们都会有不好的感觉。这不仅会损害当前客户体验,而且会对您的品牌和客户关系产生长期影响。
因此...如何减少缺货?防止缺货的三个步骤如下
对影响缺货的因素(包括库存水平)进行头脑风暴分
防止缺货的最大因素是现有的库存水平。如果库存中没有足够的产品,将面临缺货。但现有库存只是一个因素。您还需要了解影响移动供应链的所有因素(如在途库存、销售额预测、历史销售业绩),甚至还需要了解您自己的供应商所带来的影响。
因此,如何保持库存水平足够高以满足客户需求,但又足够低以避免库存过剩?您需要对影响库存水平的因素进行头脑风暴分析。使用结构化的问题解决工具(如 CT 树或鱼骨图)可以让您获得成功。
下面是一个头脑风暴工具示例,该示例使用 Minitab Workspace 中的鱼骨图。
收集数据
一旦确定了影响缺货的关键因素,就需要收集有关这些因素的数据。请注意,可能需要从多个来源和系统收集库存数据,而且数据的请求和准备过程可能需要一些时间。考虑需要收集的数据量。
例如,考虑到一段时间发生的所有变化,若追溯到 5 年前可能太久了。收集几个月的数据可能更合理,所以请根据您的最佳判断来捕获您的过程的代表性快照。您可以请 IT 部门协助,或利用功能强大的数据统一工具(如 Minitab Connect)访问、集成和准备要分析的数据。
使用预测分析来分析数据
收集到数据之后,就可以开始进行最有趣的部分:分析!传统的业务分析和可视化技术在这方面可能存在不足,因为最有可能出现的直观效果是:现有库存越低,缺货量越大!由于我们已经知道这一点,因此我们真正想要确定的是:是否还有另一个重要因素是缺货的关键驱动因素?是否存在一个最佳库存水平既可最大限度地减少缺货,又不会造成积压和生产过剩?
因此,为什么要进行预测分析?简言之,设想创建一个方程,该方程将所有影响缺货的因素作为预测变量,并将缺货作为响应。就像高中代数一样,这些不同的因素有不同的权重,因此对结果的影响程度也不同。在 Minitab,我们开发了解决方案来专门帮助您解决这些问题! 收起阅读 »
假设检验的功效和样本数量
在假设检验中,我们会使用样本中的数据来描绘有关总体的结论。首先,我们会进行假设,这被称为原假设(以 H0 表示)。当您进行原假设时,您也需要定义备选假设 (Ha),其与原假设正相反。样本数据将用于判断 H0 是否可以被否定。如果其被否定,则统计结论将认为备选假设 Ha 正确。
请记住这一检验的功效,或是在原假设不正确时,原假设被否定的可能性。
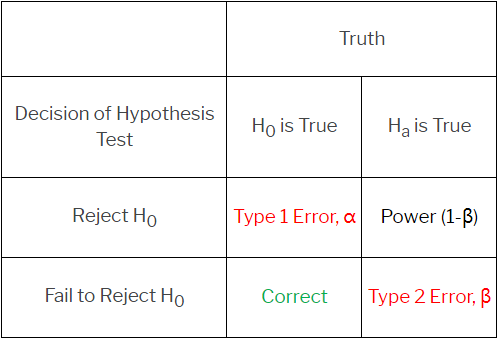
它可以解释为“检验在应该拒绝原假设时拒绝原假设的能力”。如果原假设不正确,则有很高概率拒绝原假设是很有意义的。功效与类型 2 的错误相关(功效 = 1 - 类型 2 错误),请见下表。类型 2 错误是当备选假设正确时不拒绝原假设的概率。因此,确保有足够高的功效,才能保证类型 2 错误较低或“可以接受”。确保检验有足够功效的一种常用方法是收集足够的数据,因为功效的计算取决于样本数量等因子。样本数量越大,功效越高。换言之,未能收集足够的数据将导致低功效和大量类型 2 错误。
最重要的是要找到合适的样本数量。显而易见,未能收集足够的数据会导致更多的类型 2 错误。但是,收集“过多”的数据也会增加类型 1 错误,因为检验的功效会更高。因此,该检验可能会检测到与假设值的微小差异,即使该差异可能没有任何实际意义,尤其是与抽样成本有关时。检验功效的计算应当基于实际意义。
MINITAB具有通过多种不同统计检验计算功效的功能
在下列示例中,分析人员在 Minitab 中通过单比率检验和单样本 t 检验,进行了功效和样本数量分析。
单比率检验样本数量
考虑将产品分类为好或差的制造过程,其中有 1% 的不良品率。如果不良品率上升至 3%,则会对整个组织造成严重的成本问题。他们需要确定合适的样本数量,以满足:类型 I 错误率为 0.05,检验功效为 0.80,以检测出不良品率从 1% 上升至 3% 或更高。
因为分析人员对不良品率研究感兴趣,他们使用了单比率检验。原假设和备选假设是:
Ho: P = 0.01
Ha: P > 0.01
其中 P 为实际缺陷比率。
为了找出需要多少数据点才能达到至少0.8的功效,分析人员在 Minitab 中进行了单比率检验的功效和样本数量分析。
单样本 t 检验的样本数量
将产品分类为好或差很简单,但会损失很多信息。将好产品视为在 5 到 10 之间。假如有 2 个单元测得的数值为 4.9 和 10.01,并因而归入差的分类。假如有另外 2 个单元测得的数值为 2.3 和 14.1,并因而归入差的分类。请注意,如果只是简单的区分好和差,这两种情况是相同的。因此,如果测量产品质量特征是可行的,那么分析人员应该记录质量特征的实际值,并使用记录的数据 – 无需转换为好和差。单样本 t 检验可以用于检验总体的均值是否与目标一致。如果样本数据的均值接近“目标”,则该过程可能运行良好。如果均值不接近目标,则可能生产出缺陷产品。
例如,假设该产品特征为特定目标的孔直径。分析人员可以测量每个产品上的孔直径,并使用单样本 t 检验将均值与目标值进行比较,而不是检查 236 个产品以确定孔是否符合规格。
为了找出需要多少数据点来检测至少 80% 功效的过程均值中的 1 西格玛偏移,分析人员在 Minitab 中对一个单样本 t 检验进行功效和样本数量分析。
计算的样本数量仅为 10。这意味着如果分析人员希望确定目标的偏离均值是否超过了 1 西格玛,则他们需要进行 10 个单位的单样本 t 检验,以获得至少 80% 的功效。
为什么会有这么大的区别?
属性数据的假设检验需要大量样本,因为在收集数据时没有获取详细信息。另一方面,连续数据的假设检验只需较少的样本数量,因为其获取并使用了产品的详细信息。该理论不仅适用于功效。属性数据需要大量样本以用于置信区间、属性一致性分析、控制图和能力分析。
总之,重要的是进行具有足够功效的假设检验,以提供合理的机会来检测差异。功效与样本数量直接相关。Minitab 具有计算多种不同假设检验(包括试验设计)的功效的功能。
本文最初出现在Minitab博客上。
收起阅读 »
请记住这一检验的功效,或是在原假设不正确时,原假设被否定的可能性。
它可以解释为“检验在应该拒绝原假设时拒绝原假设的能力”。如果原假设不正确,则有很高概率拒绝原假设是很有意义的。功效与类型 2 的错误相关(功效 = 1 - 类型 2 错误),请见下表。类型 2 错误是当备选假设正确时不拒绝原假设的概率。因此,确保有足够高的功效,才能保证类型 2 错误较低或“可以接受”。确保检验有足够功效的一种常用方法是收集足够的数据,因为功效的计算取决于样本数量等因子。样本数量越大,功效越高。换言之,未能收集足够的数据将导致低功效和大量类型 2 错误。
最重要的是要找到合适的样本数量。显而易见,未能收集足够的数据会导致更多的类型 2 错误。但是,收集“过多”的数据也会增加类型 1 错误,因为检验的功效会更高。因此,该检验可能会检测到与假设值的微小差异,即使该差异可能没有任何实际意义,尤其是与抽样成本有关时。检验功效的计算应当基于实际意义。
MINITAB具有通过多种不同统计检验计算功效的功能
在下列示例中,分析人员在 Minitab 中通过单比率检验和单样本 t 检验,进行了功效和样本数量分析。
单比率检验样本数量
考虑将产品分类为好或差的制造过程,其中有 1% 的不良品率。如果不良品率上升至 3%,则会对整个组织造成严重的成本问题。他们需要确定合适的样本数量,以满足:类型 I 错误率为 0.05,检验功效为 0.80,以检测出不良品率从 1% 上升至 3% 或更高。
因为分析人员对不良品率研究感兴趣,他们使用了单比率检验。原假设和备选假设是:
Ho: P = 0.01
Ha: P > 0.01
其中 P 为实际缺陷比率。
为了找出需要多少数据点才能达到至少0.8的功效,分析人员在 Minitab 中进行了单比率检验的功效和样本数量分析。
单样本 t 检验的样本数量
将产品分类为好或差很简单,但会损失很多信息。将好产品视为在 5 到 10 之间。假如有 2 个单元测得的数值为 4.9 和 10.01,并因而归入差的分类。假如有另外 2 个单元测得的数值为 2.3 和 14.1,并因而归入差的分类。请注意,如果只是简单的区分好和差,这两种情况是相同的。因此,如果测量产品质量特征是可行的,那么分析人员应该记录质量特征的实际值,并使用记录的数据 – 无需转换为好和差。单样本 t 检验可以用于检验总体的均值是否与目标一致。如果样本数据的均值接近“目标”,则该过程可能运行良好。如果均值不接近目标,则可能生产出缺陷产品。
例如,假设该产品特征为特定目标的孔直径。分析人员可以测量每个产品上的孔直径,并使用单样本 t 检验将均值与目标值进行比较,而不是检查 236 个产品以确定孔是否符合规格。
为了找出需要多少数据点来检测至少 80% 功效的过程均值中的 1 西格玛偏移,分析人员在 Minitab 中对一个单样本 t 检验进行功效和样本数量分析。
计算的样本数量仅为 10。这意味着如果分析人员希望确定目标的偏离均值是否超过了 1 西格玛,则他们需要进行 10 个单位的单样本 t 检验,以获得至少 80% 的功效。
为什么会有这么大的区别?
属性数据的假设检验需要大量样本,因为在收集数据时没有获取详细信息。另一方面,连续数据的假设检验只需较少的样本数量,因为其获取并使用了产品的详细信息。该理论不仅适用于功效。属性数据需要大量样本以用于置信区间、属性一致性分析、控制图和能力分析。
总之,重要的是进行具有足够功效的假设检验,以提供合理的机会来检测差异。功效与样本数量直接相关。Minitab 具有计算多种不同假设检验(包括试验设计)的功效的功能。
本文最初出现在Minitab博客上。
收起阅读 »
如何使用流程图来抗击病毒并保障医疗人员的安全
有关新冠病毒的新闻报道遍布各大媒体。但并非所有的新闻都是坏消息。人类的意志坚不可摧,全球各地都在努力研发病毒疫苗。医疗系统正在经受着前所未有的考验。但是,面临困境,依然有许多像Adventist HealthCare这样的组织在奋起抗击病毒。
利用卓越运营应对新冠病毒
总部位于盖瑟斯堡的 Adventist Healthcare 成立于1907年,是马里兰州蒙哥马利县的第一家(也是最大一家)医疗提供商。旗下的医疗系统包括四家医院、1,700多名医生和医疗人员、5,500多名员工以及由诸多医疗中心和设施组成的综合医疗网络,其服务不仅涵盖马里兰州,还覆盖华盛顿特区。
在美国确认新冠肺炎病例之后,Adventist HealthCare 卓越运营团队立即行动起来。他们组织了定期会议,力求在医生的领导以及其他多学科团队成员的参与下,组成过程设计和改进团队,共同分享有关此全球性新冠病毒的一切可用信息。世界卫生组织(WHO)和美国疾病防控中心(CDC)倡导增强卫生消毒方法以及严格限制身体接触,这让卓越运营团队意识到,只有更新医院和护理中心的现有诊治过程,才能更好地保护设施内的医疗人员和患者。
在 Melany Rabideau 的领导下,卓越运营团队在 Minitab Engage 中创建了一个项目,以期在单一位置记录与新冠病毒相关的所有过程。然后他们开始审查并确定哪些过程需要改进。
创建并更新过程,防止传染扩散
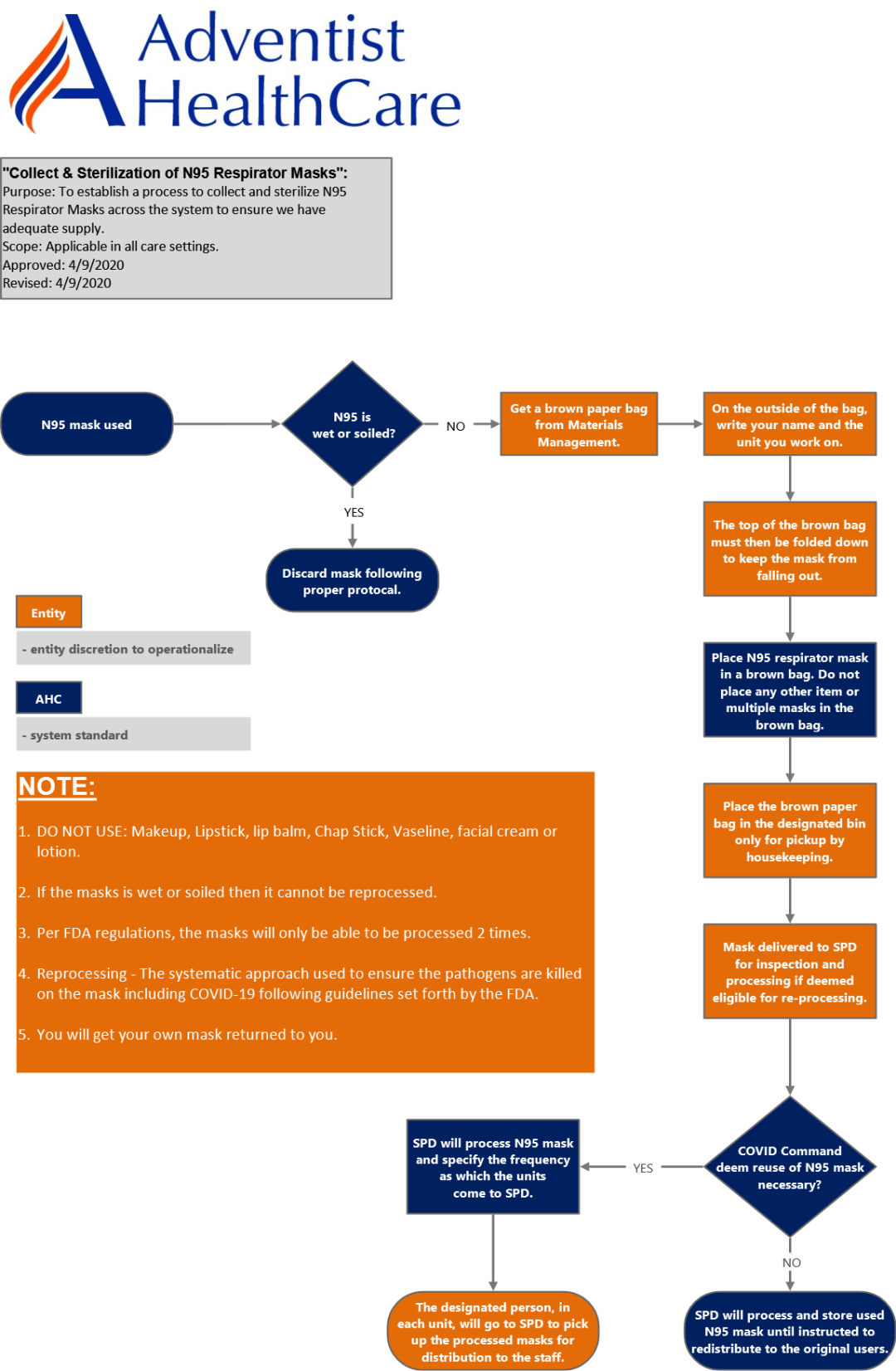
在弄清楚哪些过程需要改进以及需要创建哪些过程后,卓越运营团队立即展开行动。由于美国个人防护装备需求水涨船高,供应短缺,作为口罩供应稀缺时确保医疗人员安全的预防措施,卓越运营团队在 Minitab Engage 中创建了流程图,以确立在其所有设施中对N95口罩进行回收和消毒的标准化方法。
与任何优秀的流程图一样,卓越运营团队精心制定了完成过程所需的所有具体步骤,同时还添加了备注和颜色键来帮助医疗人员轻松快速地理解流程图。
以下是他们的流程图的数字版。
他们将流程图妥善分发到整个医疗系统中。但是,随着时间的推移,CDC 和 Adventist 领导层的指导方针发生了改变。
万幸的是,由于流程图是使用 Minitab Engage 创建,卓越运营团队中的任何人都可以根据需要进行编辑。团队成员非常喜欢这一点。他们将 Minitab Engage 当作“唯一参考信息源”和“中央存储库”,让所有团队成员都能在统一位置轻松获取相同的信息。
Adventist HealthCare 的脚步从未停歇
在当下全球疫情期间,Adventist HealthCare 创建了多张流程图来支持和帮助他们的医疗人员,针对 N95 口罩回收和消毒的流程图仅仅是其中之一。以下是他们与我们分享的其他两张流程图:
新冠肺炎疫情期间的紧急抢救响应
治疗导航 - 紧急治疗的调查病例 (PUI) 跟进过程
抗击新冠病毒正在如火如荼地进行,Adventist HealthCare 仍在不断创建新的流程图并予以更新,同时也在为其回归正轨做好规划准备。其中一名团队成员说得非常好:“Minitab Engage 在混乱时刻给予组织一种有条不紊的感觉。” 收起阅读 »
利用卓越运营应对新冠病毒
总部位于盖瑟斯堡的 Adventist Healthcare 成立于1907年,是马里兰州蒙哥马利县的第一家(也是最大一家)医疗提供商。旗下的医疗系统包括四家医院、1,700多名医生和医疗人员、5,500多名员工以及由诸多医疗中心和设施组成的综合医疗网络,其服务不仅涵盖马里兰州,还覆盖华盛顿特区。
在美国确认新冠肺炎病例之后,Adventist HealthCare 卓越运营团队立即行动起来。他们组织了定期会议,力求在医生的领导以及其他多学科团队成员的参与下,组成过程设计和改进团队,共同分享有关此全球性新冠病毒的一切可用信息。世界卫生组织(WHO)和美国疾病防控中心(CDC)倡导增强卫生消毒方法以及严格限制身体接触,这让卓越运营团队意识到,只有更新医院和护理中心的现有诊治过程,才能更好地保护设施内的医疗人员和患者。
在 Melany Rabideau 的领导下,卓越运营团队在 Minitab Engage 中创建了一个项目,以期在单一位置记录与新冠病毒相关的所有过程。然后他们开始审查并确定哪些过程需要改进。
创建并更新过程,防止传染扩散
在弄清楚哪些过程需要改进以及需要创建哪些过程后,卓越运营团队立即展开行动。由于美国个人防护装备需求水涨船高,供应短缺,作为口罩供应稀缺时确保医疗人员安全的预防措施,卓越运营团队在 Minitab Engage 中创建了流程图,以确立在其所有设施中对N95口罩进行回收和消毒的标准化方法。
与任何优秀的流程图一样,卓越运营团队精心制定了完成过程所需的所有具体步骤,同时还添加了备注和颜色键来帮助医疗人员轻松快速地理解流程图。
以下是他们的流程图的数字版。
他们将流程图妥善分发到整个医疗系统中。但是,随着时间的推移,CDC 和 Adventist 领导层的指导方针发生了改变。
万幸的是,由于流程图是使用 Minitab Engage 创建,卓越运营团队中的任何人都可以根据需要进行编辑。团队成员非常喜欢这一点。他们将 Minitab Engage 当作“唯一参考信息源”和“中央存储库”,让所有团队成员都能在统一位置轻松获取相同的信息。
Adventist HealthCare 的脚步从未停歇
在当下全球疫情期间,Adventist HealthCare 创建了多张流程图来支持和帮助他们的医疗人员,针对 N95 口罩回收和消毒的流程图仅仅是其中之一。以下是他们与我们分享的其他两张流程图:
新冠肺炎疫情期间的紧急抢救响应
治疗导航 - 紧急治疗的调查病例 (PUI) 跟进过程
抗击新冠病毒正在如火如荼地进行,Adventist HealthCare 仍在不断创建新的流程图并予以更新,同时也在为其回归正轨做好规划准备。其中一名团队成员说得非常好:“Minitab Engage 在混乱时刻给予组织一种有条不紊的感觉。” 收起阅读 »
SPC 之 I-MR 控制图
概述
1924 年,美国的休哈特博士应用统计数学理论将 3Sigma 原理运用于生产过程中,并发表了著名的“控制图法”,对产品特性和过程变量进行控制,开启了统计过程控制新时代。
什么是控制图
控制图指示过程何时不受控制,有助于标识是否存在特殊原因变异。如果存在特殊原因变异,则说明过程不稳定且有必要采取纠正措施。
控制图是按时间排序顺序绘制过程数据的图。大多数控制图都包括一条中心线、一个控制上限和一个控制下限。中心线表示过程均值。控制限表示过程变异。默认情况下,控制限绘制在中心线上下 3σ 的位置。
随机位于控制限内的点指示过程受控制且仅显示常见原因变异。位于控制限外部或者显示非随机模式的点指示过程不受控制且存在特殊原因变异。
如何选择合适的控制图
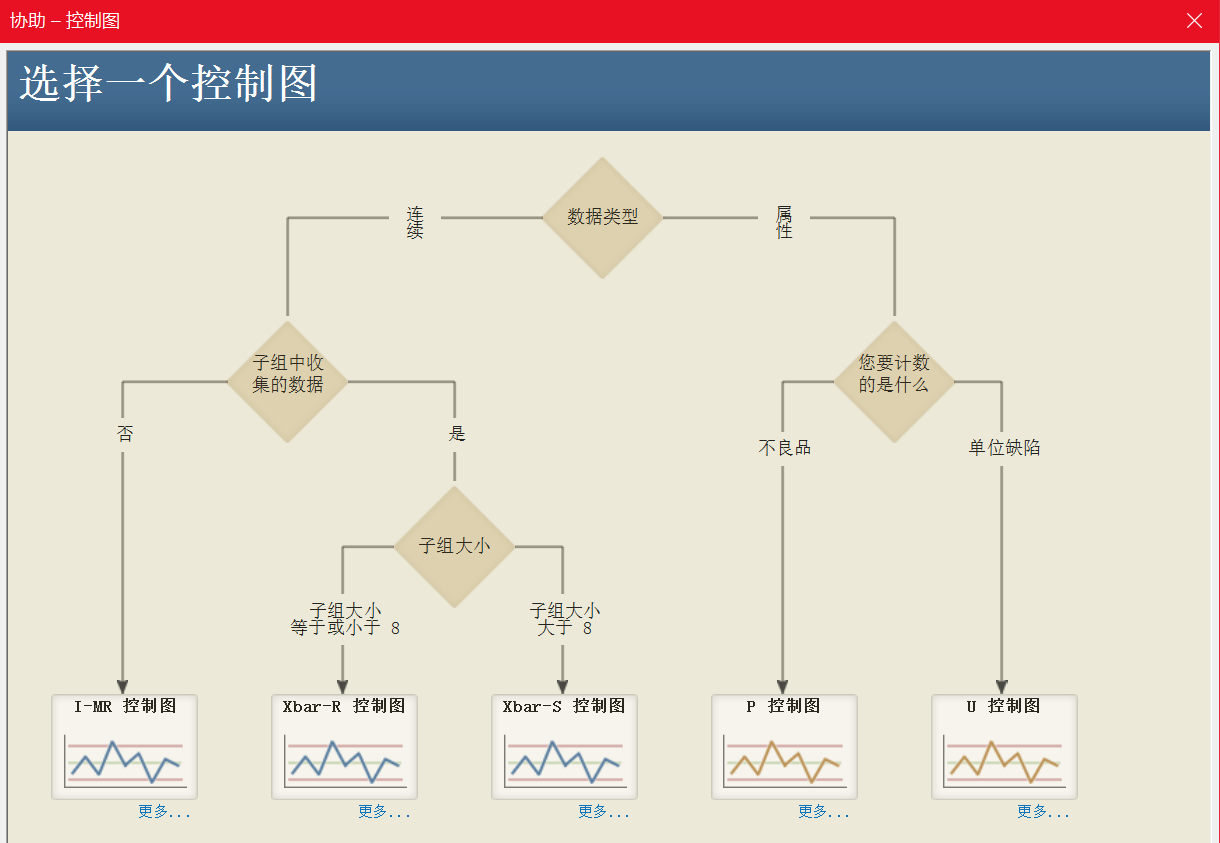
随着控制图的发展,它的类型也是越来越多,那么这时候对于使用 Minitab 的朋友来说,经常会纠结如何去选择一个合适的控制图。在 Minitab 19 中,协助菜单可以很好的帮助我们去选择一个合适的控制图。
I-MR 控制图
今天,我们来绘制一下 I-MR 控制图。
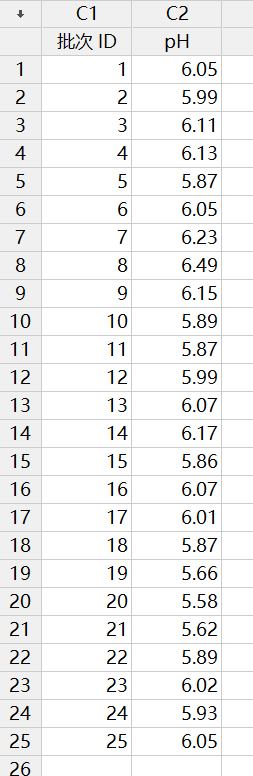
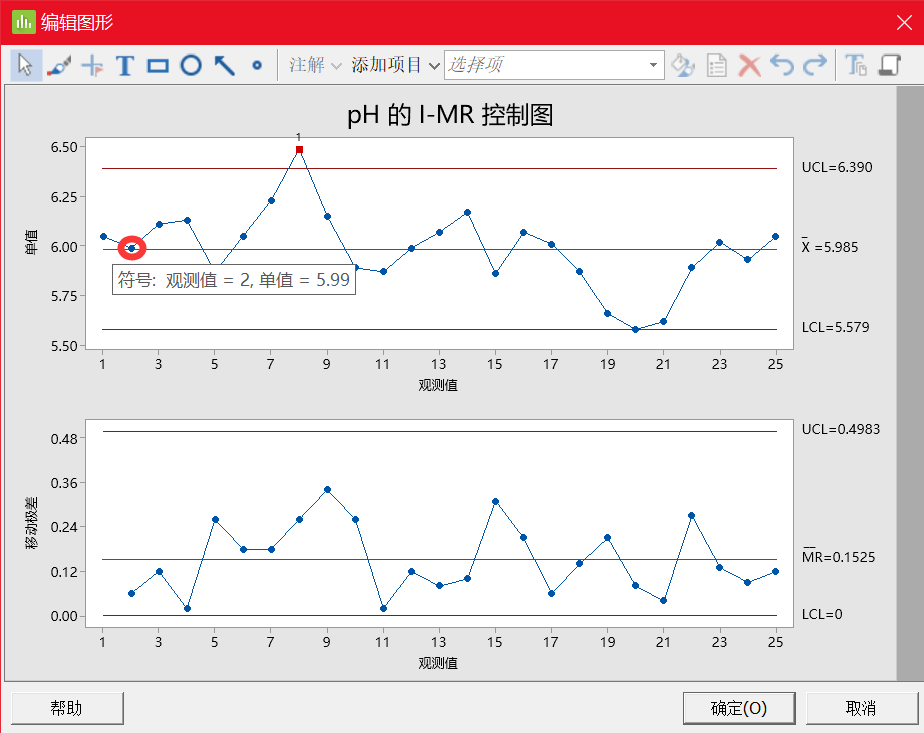
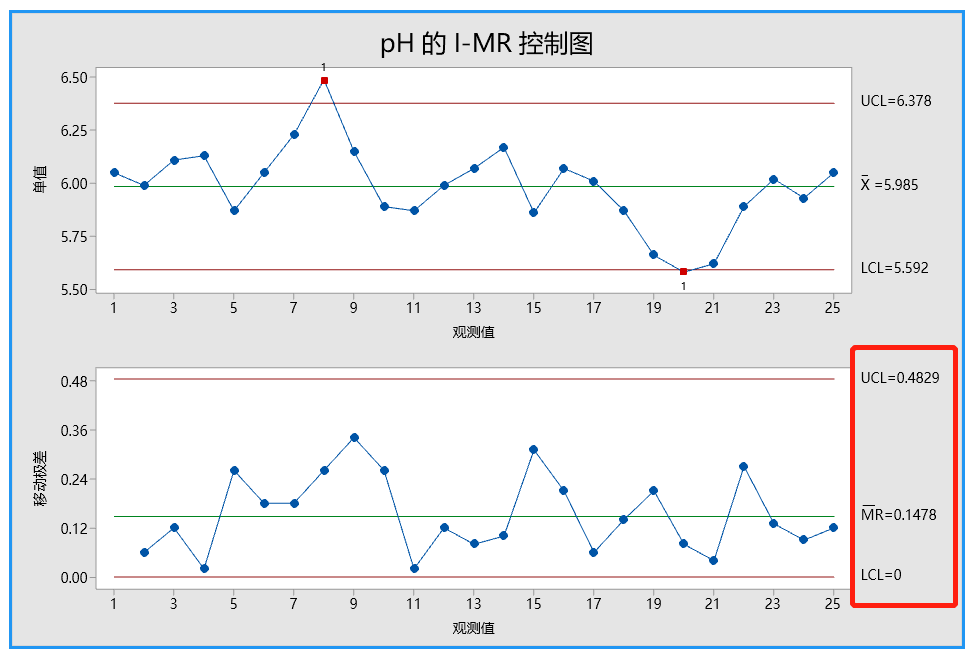
问题背景:某质量工程师监控了液体洗涤剂的生产过程,想要评估该过程是否受控制。这位工程师测量了 25 个连续批次的洗涤剂的 pH 值。
由于 pH 值的数据类型是连续型数据,而且是每批次只取一个样品(子组大小等于 1),故这位工程师创建了一张 I-MR 控制图,以监控洗涤剂的生产过程。
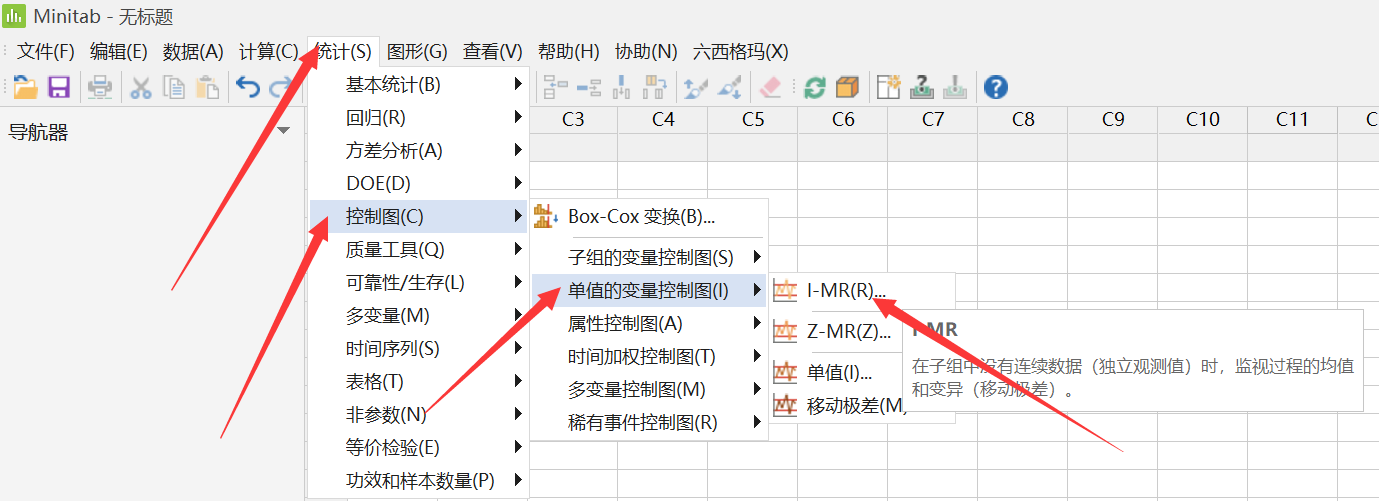
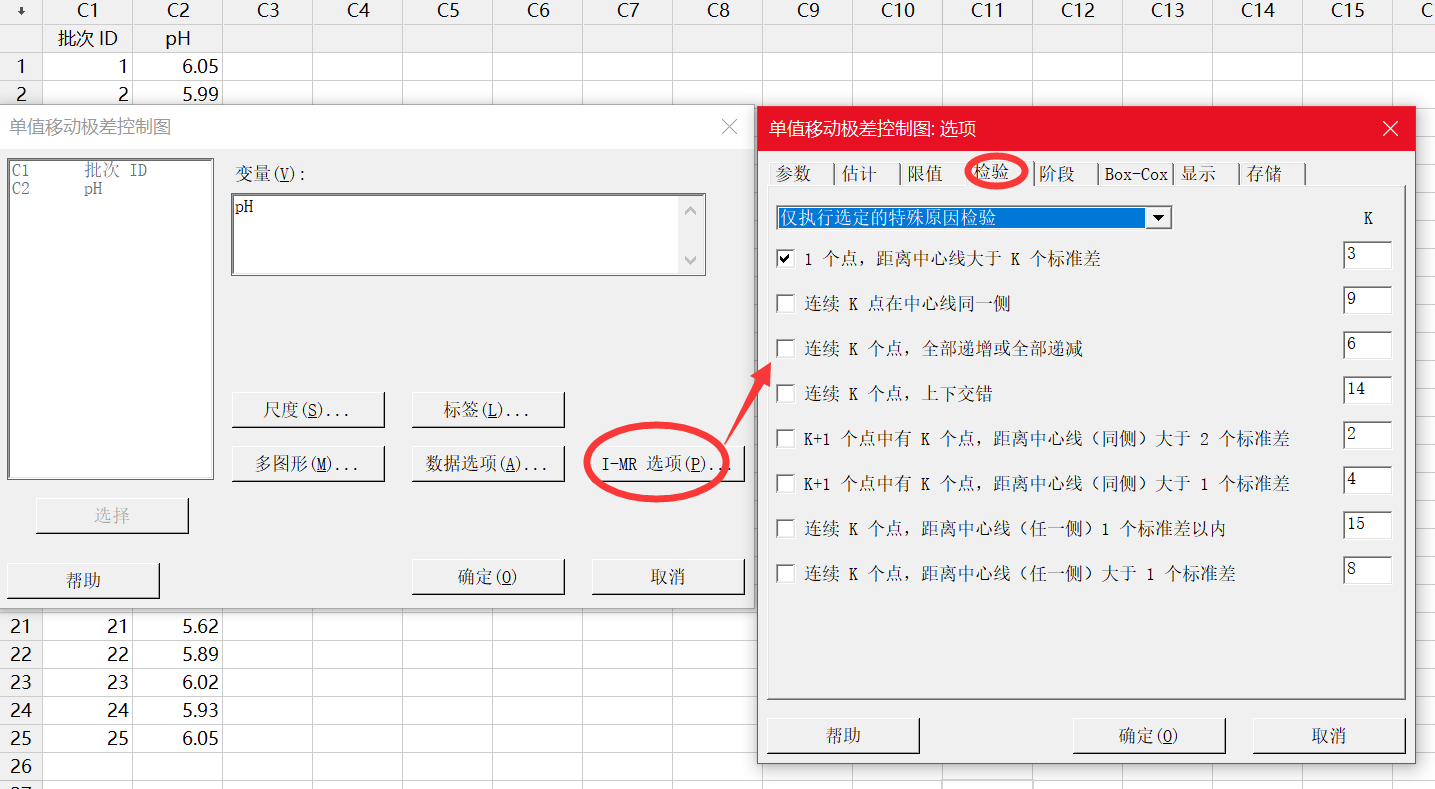
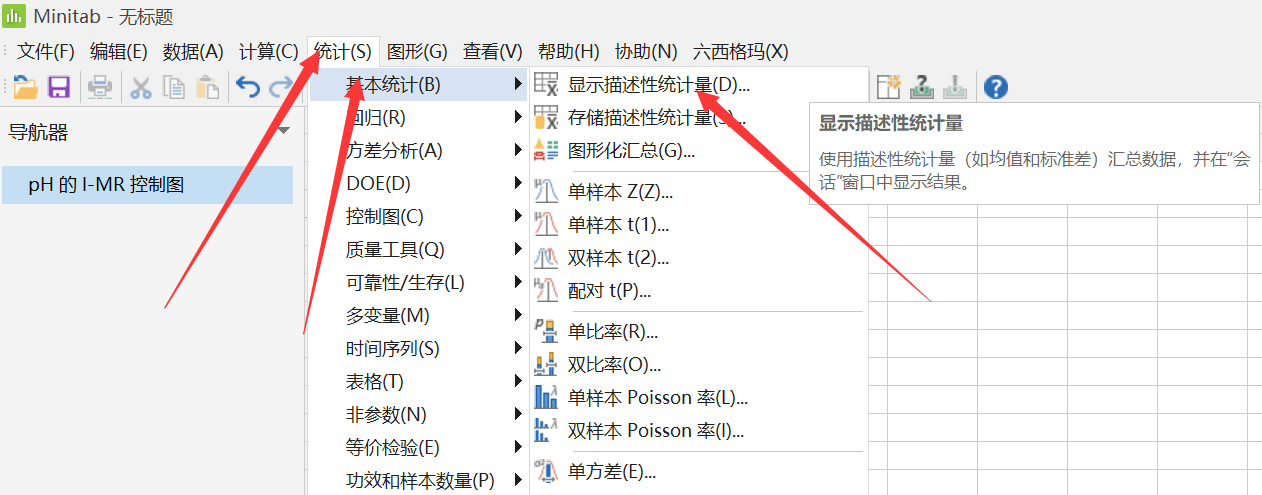
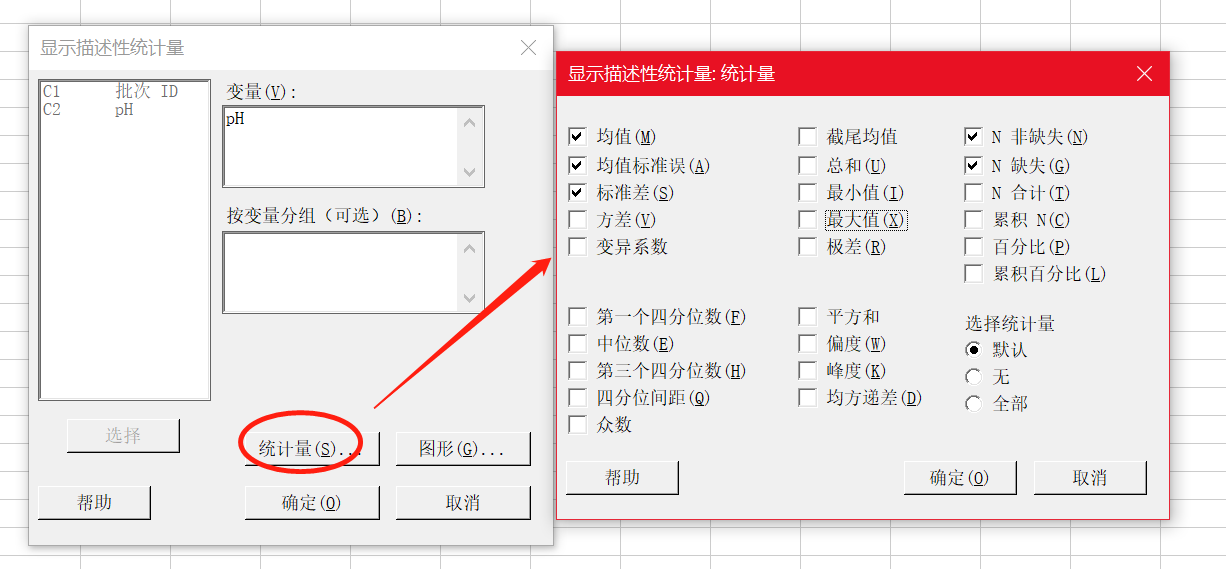
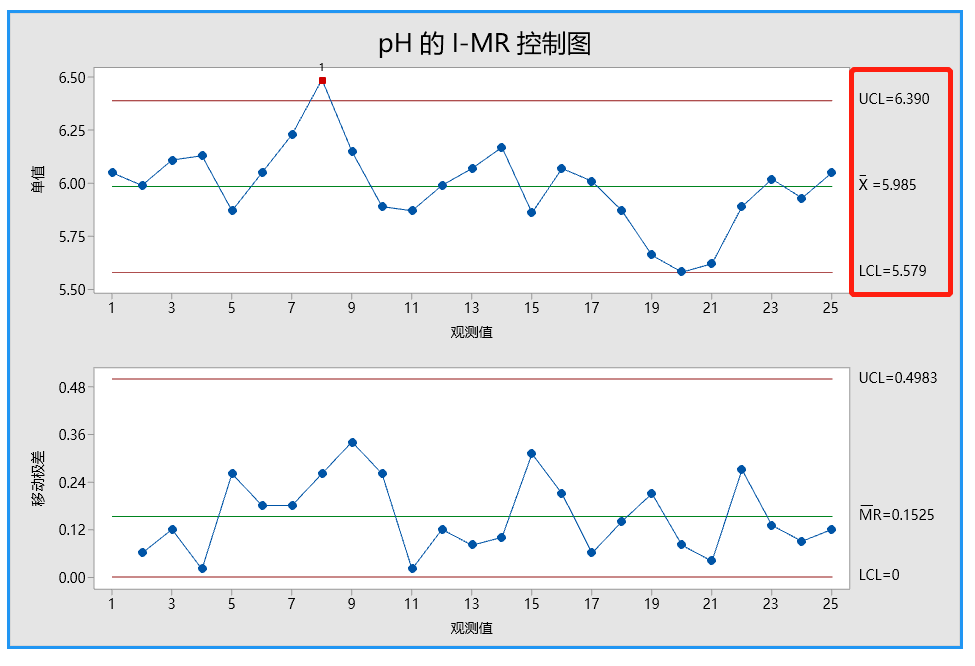
Minitab 绘制 I-MR 控制图
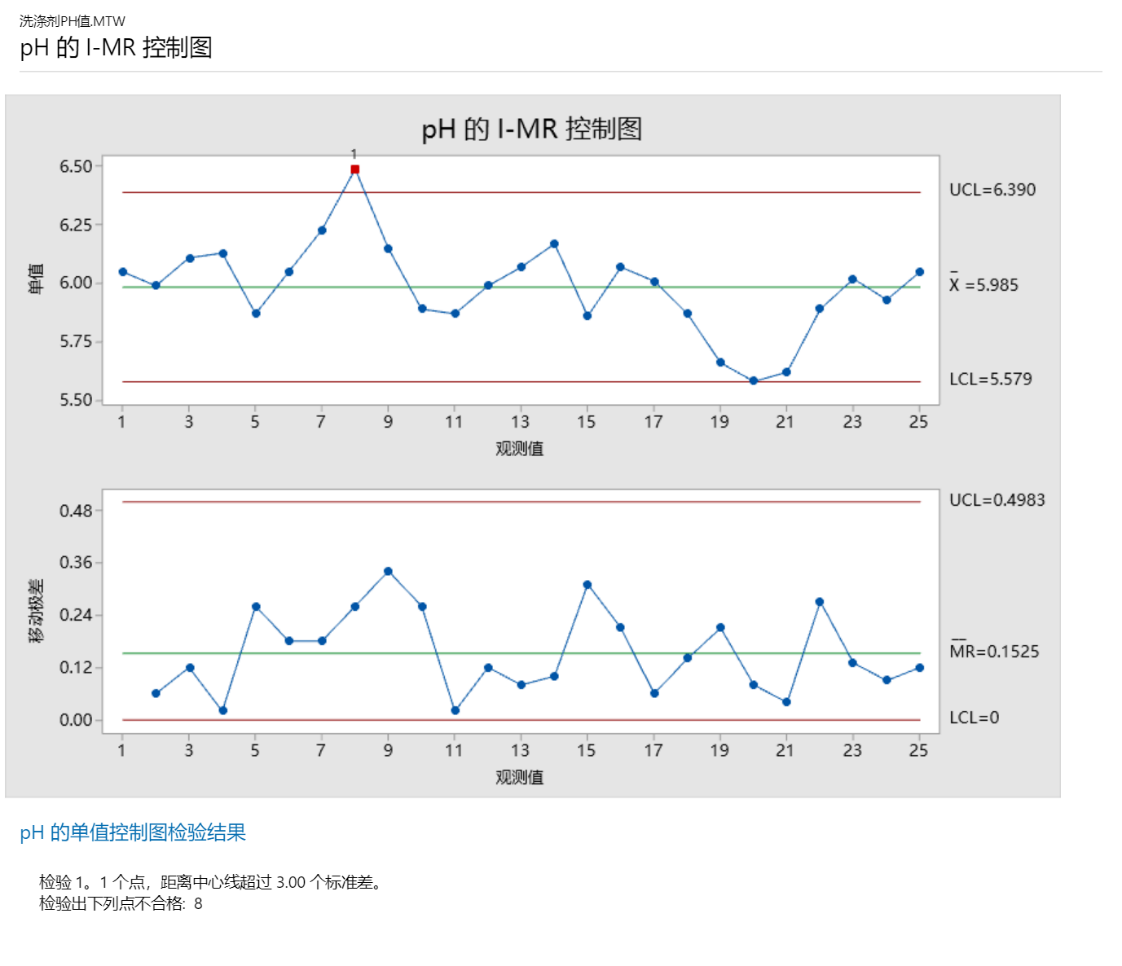
Minitab 结果解释
首先解释移动极差控制图(MR 控制图)以检查过程变异。没有位于控制限外部的点且所有的点都显示出随机模式。因此,过程变异受控制,质量工程师可以检查单值控制图(I 控制图)上的过程中心。
I 控制图上的一个观测值在检验 1 中失败,因为观测值在中心线上方且距离中心线超过 3个标准差。
I-MR 控制图的控制限计算(手动)
对于 I-MR 控制图,包含两张图单值控制图(I 控制图)和移动极差控制图(MR 控制图), 我们首先来认识一下这两张图形上的 X 轴、Y 轴、点和线分别表示什么含义。
一、单值控制图(I 控制图)
X 轴:批次 ID
Y 轴:单值(每个批次对应的 pH 值,如单值图上的第二个点表示的是批次 2 的 pH 值)
点:单值控制图(I 控制图)上的每个标绘点是单独的观测值(如上图)。
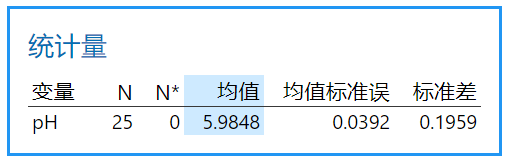
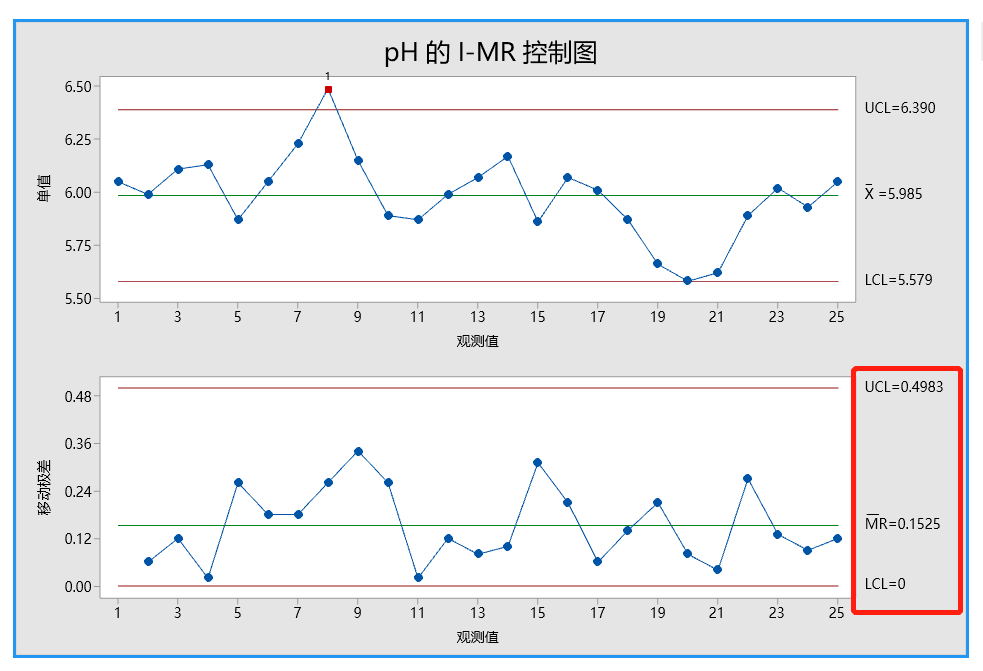
中心线:单值控制图(I 控制图)上的中心线是过程平均值的估计值,计算如下
控制限:单值控制图(I 控制图)控制限的计算结果取决于标准差的估计方式。
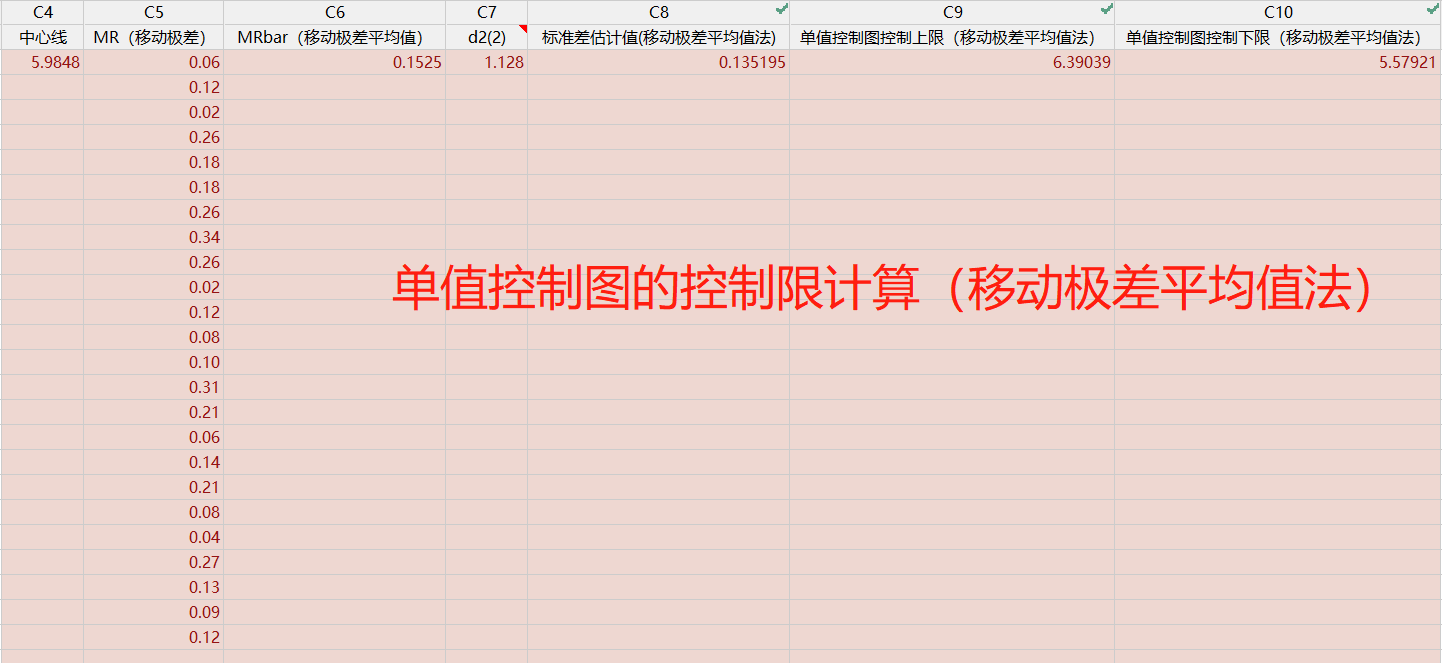
1)移动极差平均值(默认方法)-移动极差长度默认为 2
a. 计算移动极差 MR(相邻 2 个数的较大值减较小值),当前数据样本量为 25,计算得到24 个移动极差。
b. 计算这 24 个移动极差的平均值 MRbar
c. 估计标准差的公式如下:
控制限计算公式
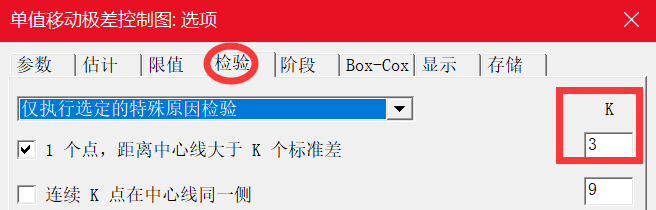
其中 k 为检验 1 的参数。默认值为 3。
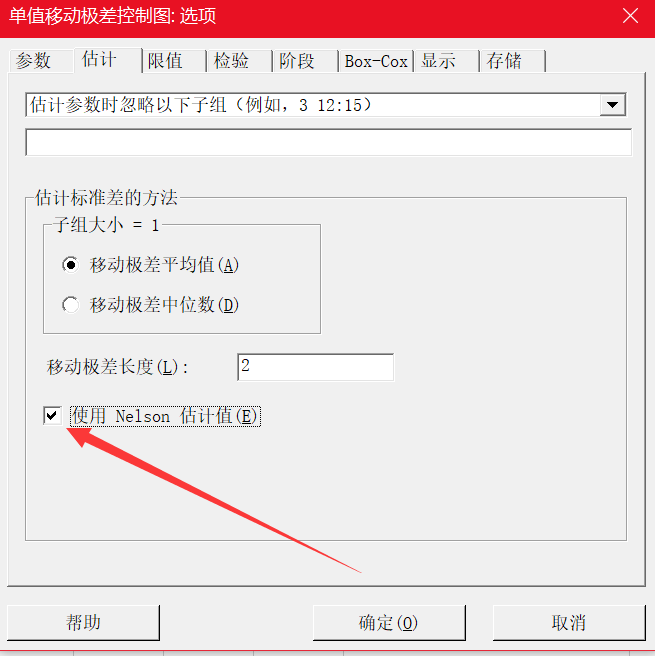
当选择默认的用移动极差平均值来估计标准差时,我们还可以勾选”使用 Nelson 估计值”。使用 Nelson 估计值可以在计算控制限时更正异常大的移动极差值。此过程与 Nelson1 提出的过程相似。Minitab 消除比移动极差平均值大 3σ 的任何移动极差值,然后重新计算移动极差平均值和控制限。
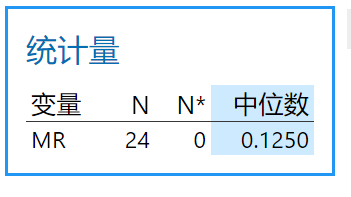
2)移动极差中位数
a. 计算移动极差
b. 计算移动极差中位数
c. 估计标准差的公式如下:
二、移动极差控制图(MR 控制图)
X 轴:批次 ID
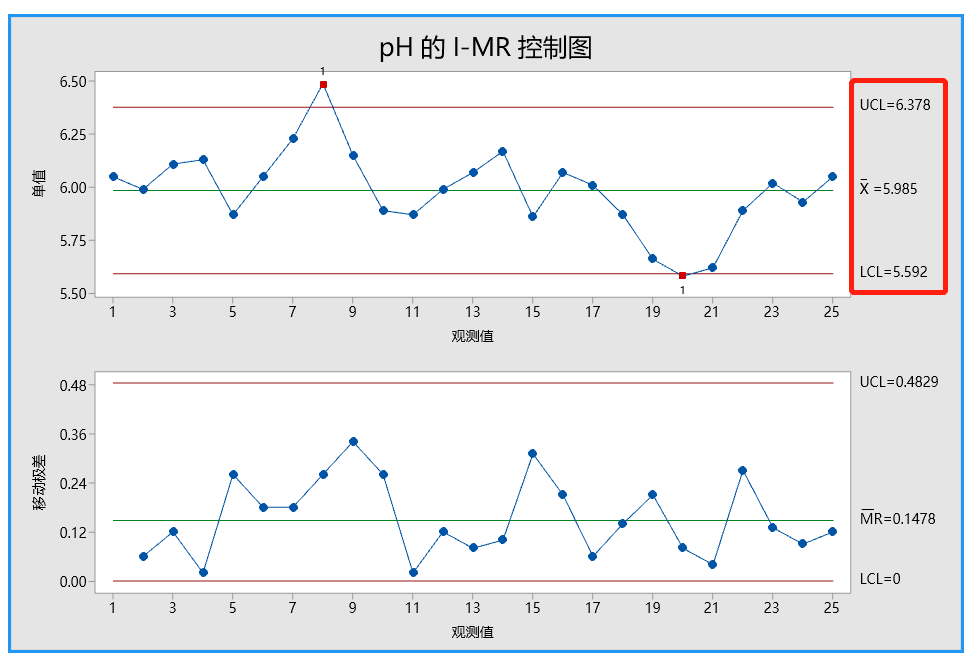
Y 轴:移动极差(如下 MR 控制图中的第二个点是批次 2 的 pH 值 5.99 和批次 3pH 值 6.11中较大值减去较小值,结果为 0.12(6.11-5.99)
点:MR 控制图上的标绘点是移动极差(移动极差是两个或多个连续点之间差值的绝对值)。
中心线:中心线是移动极差平均值的无偏估计值 MRbar
控制上限:??? = (??(?) ⋅ ?) + (? ⋅ ??(?) ⋅ ?)
控制下限:??? = (??(?) ⋅ ?) − (? ⋅ ??(?) ⋅ ?)或 LCL=0(计算结果为负值时)
移动极差平均值法的结果
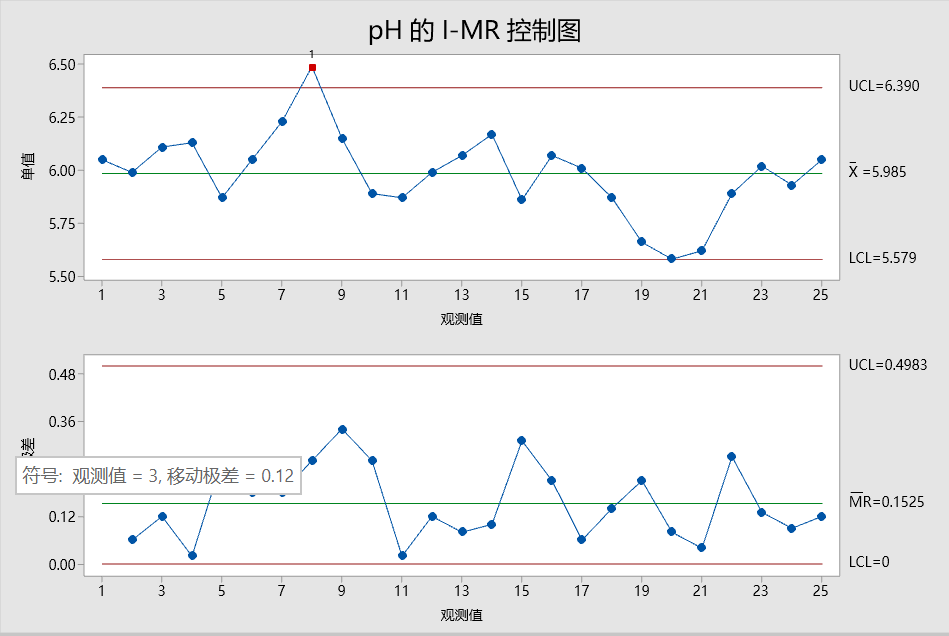
移动极差中位数法的结果
结论
手动计算的过程比较复杂,而且还可能会出错,但是有了 Minitab 的帮助,我们只需要选择好合适的控制图后,点击几下就可以高效快速的计算出对应的控制限。当然,花点时间手动计算一下这些值,能够帮助你更好的理解控制图。而且在计算的过程中,你也会发现 Minitab 的算法跟 Excel 中算法的差异,也能够发现单值控制图的控制限受到移动极差的影响,所以在分析这两张控制图时,应该先分析下面的移动极差控制图,移动极差控制图中没有异常点时,这时候分析单值控制图才是有意义的。
X 轴:批次 ID
Y 轴:移动极差(如下 MR 控制图中的第二个点是批次 2 的 pH 值 5.99 和批次3pH 值 6.11 中较大值减去较小值,结果为 0.12(6.11-5.99) 收起阅读 »
1924 年,美国的休哈特博士应用统计数学理论将 3Sigma 原理运用于生产过程中,并发表了著名的“控制图法”,对产品特性和过程变量进行控制,开启了统计过程控制新时代。
什么是控制图
控制图指示过程何时不受控制,有助于标识是否存在特殊原因变异。如果存在特殊原因变异,则说明过程不稳定且有必要采取纠正措施。
控制图是按时间排序顺序绘制过程数据的图。大多数控制图都包括一条中心线、一个控制上限和一个控制下限。中心线表示过程均值。控制限表示过程变异。默认情况下,控制限绘制在中心线上下 3σ 的位置。
随机位于控制限内的点指示过程受控制且仅显示常见原因变异。位于控制限外部或者显示非随机模式的点指示过程不受控制且存在特殊原因变异。
如何选择合适的控制图
随着控制图的发展,它的类型也是越来越多,那么这时候对于使用 Minitab 的朋友来说,经常会纠结如何去选择一个合适的控制图。在 Minitab 19 中,协助菜单可以很好的帮助我们去选择一个合适的控制图。
I-MR 控制图
今天,我们来绘制一下 I-MR 控制图。
问题背景:某质量工程师监控了液体洗涤剂的生产过程,想要评估该过程是否受控制。这位工程师测量了 25 个连续批次的洗涤剂的 pH 值。
由于 pH 值的数据类型是连续型数据,而且是每批次只取一个样品(子组大小等于 1),故这位工程师创建了一张 I-MR 控制图,以监控洗涤剂的生产过程。
Minitab 绘制 I-MR 控制图
Minitab 结果解释
首先解释移动极差控制图(MR 控制图)以检查过程变异。没有位于控制限外部的点且所有的点都显示出随机模式。因此,过程变异受控制,质量工程师可以检查单值控制图(I 控制图)上的过程中心。
I 控制图上的一个观测值在检验 1 中失败,因为观测值在中心线上方且距离中心线超过 3个标准差。
I-MR 控制图的控制限计算(手动)
对于 I-MR 控制图,包含两张图单值控制图(I 控制图)和移动极差控制图(MR 控制图), 我们首先来认识一下这两张图形上的 X 轴、Y 轴、点和线分别表示什么含义。
一、单值控制图(I 控制图)
X 轴:批次 ID
Y 轴:单值(每个批次对应的 pH 值,如单值图上的第二个点表示的是批次 2 的 pH 值)
点:单值控制图(I 控制图)上的每个标绘点是单独的观测值(如上图)。
中心线:单值控制图(I 控制图)上的中心线是过程平均值的估计值,计算如下
控制限:单值控制图(I 控制图)控制限的计算结果取决于标准差的估计方式。
1)移动极差平均值(默认方法)-移动极差长度默认为 2
a. 计算移动极差 MR(相邻 2 个数的较大值减较小值),当前数据样本量为 25,计算得到24 个移动极差。
b. 计算这 24 个移动极差的平均值 MRbar
c. 估计标准差的公式如下:
控制限计算公式
其中 k 为检验 1 的参数。默认值为 3。
当选择默认的用移动极差平均值来估计标准差时,我们还可以勾选”使用 Nelson 估计值”。使用 Nelson 估计值可以在计算控制限时更正异常大的移动极差值。此过程与 Nelson1 提出的过程相似。Minitab 消除比移动极差平均值大 3σ 的任何移动极差值,然后重新计算移动极差平均值和控制限。
2)移动极差中位数
a. 计算移动极差
b. 计算移动极差中位数
c. 估计标准差的公式如下:
二、移动极差控制图(MR 控制图)
X 轴:批次 ID
Y 轴:移动极差(如下 MR 控制图中的第二个点是批次 2 的 pH 值 5.99 和批次 3pH 值 6.11中较大值减去较小值,结果为 0.12(6.11-5.99)
点:MR 控制图上的标绘点是移动极差(移动极差是两个或多个连续点之间差值的绝对值)。
中心线:中心线是移动极差平均值的无偏估计值 MRbar
控制上限:??? = (??(?) ⋅ ?) + (? ⋅ ??(?) ⋅ ?)
控制下限:??? = (??(?) ⋅ ?) − (? ⋅ ??(?) ⋅ ?)或 LCL=0(计算结果为负值时)
移动极差平均值法的结果
移动极差中位数法的结果
结论
手动计算的过程比较复杂,而且还可能会出错,但是有了 Minitab 的帮助,我们只需要选择好合适的控制图后,点击几下就可以高效快速的计算出对应的控制限。当然,花点时间手动计算一下这些值,能够帮助你更好的理解控制图。而且在计算的过程中,你也会发现 Minitab 的算法跟 Excel 中算法的差异,也能够发现单值控制图的控制限受到移动极差的影响,所以在分析这两张控制图时,应该先分析下面的移动极差控制图,移动极差控制图中没有异常点时,这时候分析单值控制图才是有意义的。
X 轴:批次 ID
Y 轴:移动极差(如下 MR 控制图中的第二个点是批次 2 的 pH 值 5.99 和批次3pH 值 6.11 中较大值减去较小值,结果为 0.12(6.11-5.99) 收起阅读 »
在 Minitab 中进行扩展量具 R&R 研究
量具 R&R 研究可以告诉您测量系统生成的数据是否值得信赖。遗憾的是,严格的数据要求和其他限制可能会让量具 R&R 研究难以进行分析,并可能无法解释所有重要因子。Minitab 中的扩展量具 R&R 工具能够使这些障碍成为过去。
量具 R&R 研究可以告诉您什么?
• 您的测量系统是否足够灵敏?
• 您的测量工具是否一致?
• 进行测量的人是否一致?
扩展量具 R&R 能提供哪些额外优势?
• 不仅要分析部件和操作员,还要分析多达八个其他因子。
• 甚至不完整的数据也可以进行分析(不平衡研究)。
• 包括固定或随机因子,获得更好的灵活性。
在量具 R&R 研究中包含两个以上的因子
通常,量具 R&R 研究只关注两个因子:部件和操作员。但是如果您知道其他因子也会影响您的测量系统呢?如果您不纳入这些因子,则将永远无法了解它们对测量变异性有多大影响,以及您的测量系统可能看起来比实际情况更好还是更差。Minitab 的扩展量具 R&R 能让您纳入最多八个额外的因子,用于调查并评估所有可能影响测量系统的因子。
例如
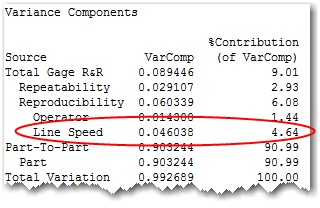
因为他们在繁忙的生产车间工作,检验人员担心生产速度的变化会影响他们的测量能力。加入生产线速度作为量具研究的因子,揭示出生产线速度变化对测量的影响甚至超出他们的预期。
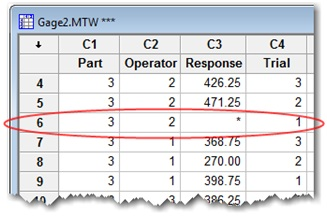
以不完整或不平衡的数据进行量具 R&R
量具 R&R 研究可以要求严格的“平衡”设计,尽管实际上数据的收集通常并不完美。也许在研究中让操作员将所有部件测量相同的次数并不可行,或者可能一些测量数据已经丢失。扩展量具 R&R 允许您分析测量系统,即使有这样不平衡的数据,也无需手动计算来解释丢失的数据。
包括固定或随机因子以获取更高的灵活性
在量具研究中,如果您有意选择了一定的兴趣级别(比如最有经验和最缺乏经验的操作员),则该因子是固定的。如果您随机选择了级别来代表总体,则该因子为随机。常见量具研究会在所有因子均为随机的基础上计算结果。但将固定因子视为随机因子可能导致过度或低估其重要性。
扩展量具 R&R 允许您指明哪些因子是固定的,哪些是随机的,以便更好更妥当地评估您的测量系统。
例如
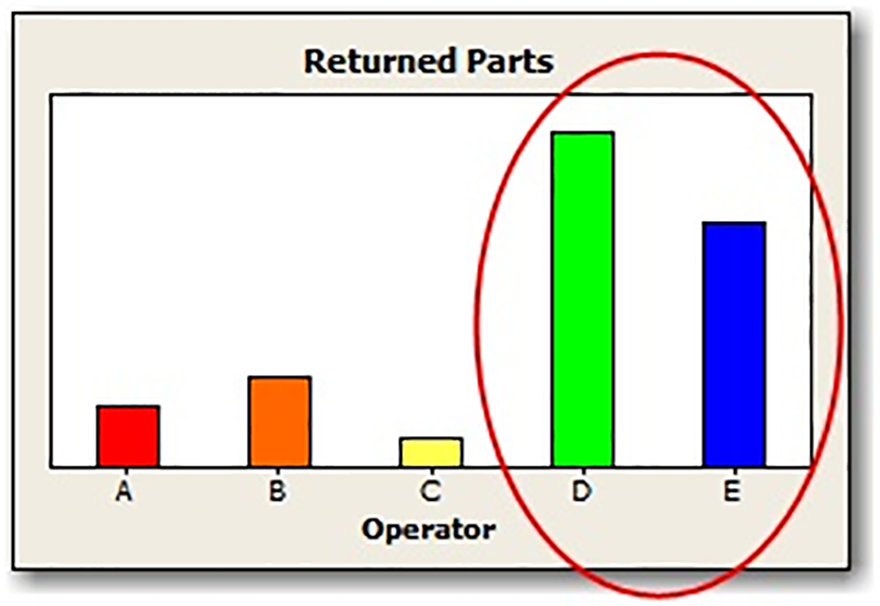
审核显示,退回精密铣削设施的大部分不合规格部件可追溯到两名经验最少的检验员。为了更好的理解该问题,质量经理希望能重点关注这些特定操作员后续的量具研究。因为人工挑选的这些操作员无法反应出随机抽样,所以在分析该研究时,经理将这一因子指定为固定因子。
MINITAB 让量具 R&R 更简单
如果您尚未利用 Minitab 的强大功能从数据中获取最大价值,请立即下载功能完备的 Minitab 30 天免费试用版。
本文最初出现在Minitab博客上。
收起阅读 »
量具 R&R 研究可以告诉您什么?
• 您的测量系统是否足够灵敏?
• 您的测量工具是否一致?
• 进行测量的人是否一致?
扩展量具 R&R 能提供哪些额外优势?
• 不仅要分析部件和操作员,还要分析多达八个其他因子。
• 甚至不完整的数据也可以进行分析(不平衡研究)。
• 包括固定或随机因子,获得更好的灵活性。
在量具 R&R 研究中包含两个以上的因子
通常,量具 R&R 研究只关注两个因子:部件和操作员。但是如果您知道其他因子也会影响您的测量系统呢?如果您不纳入这些因子,则将永远无法了解它们对测量变异性有多大影响,以及您的测量系统可能看起来比实际情况更好还是更差。Minitab 的扩展量具 R&R 能让您纳入最多八个额外的因子,用于调查并评估所有可能影响测量系统的因子。
例如
因为他们在繁忙的生产车间工作,检验人员担心生产速度的变化会影响他们的测量能力。加入生产线速度作为量具研究的因子,揭示出生产线速度变化对测量的影响甚至超出他们的预期。
以不完整或不平衡的数据进行量具 R&R
量具 R&R 研究可以要求严格的“平衡”设计,尽管实际上数据的收集通常并不完美。也许在研究中让操作员将所有部件测量相同的次数并不可行,或者可能一些测量数据已经丢失。扩展量具 R&R 允许您分析测量系统,即使有这样不平衡的数据,也无需手动计算来解释丢失的数据。
包括固定或随机因子以获取更高的灵活性
在量具研究中,如果您有意选择了一定的兴趣级别(比如最有经验和最缺乏经验的操作员),则该因子是固定的。如果您随机选择了级别来代表总体,则该因子为随机。常见量具研究会在所有因子均为随机的基础上计算结果。但将固定因子视为随机因子可能导致过度或低估其重要性。
扩展量具 R&R 允许您指明哪些因子是固定的,哪些是随机的,以便更好更妥当地评估您的测量系统。
例如
审核显示,退回精密铣削设施的大部分不合规格部件可追溯到两名经验最少的检验员。为了更好的理解该问题,质量经理希望能重点关注这些特定操作员后续的量具研究。因为人工挑选的这些操作员无法反应出随机抽样,所以在分析该研究时,经理将这一因子指定为固定因子。
MINITAB 让量具 R&R 更简单
如果您尚未利用 Minitab 的强大功能从数据中获取最大价值,请立即下载功能完备的 Minitab 30 天免费试用版。
本文最初出现在Minitab博客上。
收起阅读 »
6西格玛绿带考试随记
为了9/4的绿带考试,奋斗。。。
在充实自己的同时,提高自己。
在充实自己的同时,提高自己。
样本量大于30就可以认为是正态分布吗?你可能对中心极限定理有误区!
我经常会被问到这么一个问题:样本量多大就不用进行正态性检验了。殊不知,这问题的本身就是错误的,并不是样本大,就一定要服从正态分布。我们可以轻易举出一个反例来说明这个问题。比方说就用1-1000这一千个(甚至更多)自然数,组成一个样本,那么这个样本的分布就不是正态分布,因为1-1000服从的是均匀分布。另外,数据的分布基于形成的机理,有的分布天生就非正态(如寿命数据)。
但有些朋友,并不觉得这是一个错误的问题,甚至在他们的学习中还流传着这么一个说法:样本量大于30就可以认为是服从正态分布。当你向他问为什么的时候,会得到一个专业的解释——中心极限定理。
中心极限定理
中心极限定理(Central Limit Theorem)是统计学中最重要的结论之一。在这里,我并不想给出中心极限定理专业的定义,只需要了解它告诉我们:来自某总体的一个样本,无论该总体服从什么分布,只要样本容量足够大,其样本均值都近似服从正态分布。
请注意这里的说法:“样本均值“近似正态,而不是样本本身服从正态(不是说你抽了30个样品组成的样本数据就正态)。这里又有一个大家疑惑的地方,样本容量足够大,多大才是足够大?这个问题的答案和总体分布的形状相关,如果样本本是来自近似对称分布的总体,那么当样本量取相当小(如样本量取5)的值的时候,正态逼近的结果也会非常好。然后,如果总体的分布严重倾斜,则样本量必须取相当大的值。根据检验,对于大多数总体来说,样本容量取30或者更大,就足以得到令人满意的正态逼近结果。我想这可能就是错误认为样本量大于30就认为是正态分布的出处了。
模拟掷骰子展示中心极限定理
为了展示中心极限定理,模拟多次投掷骰子来说明。
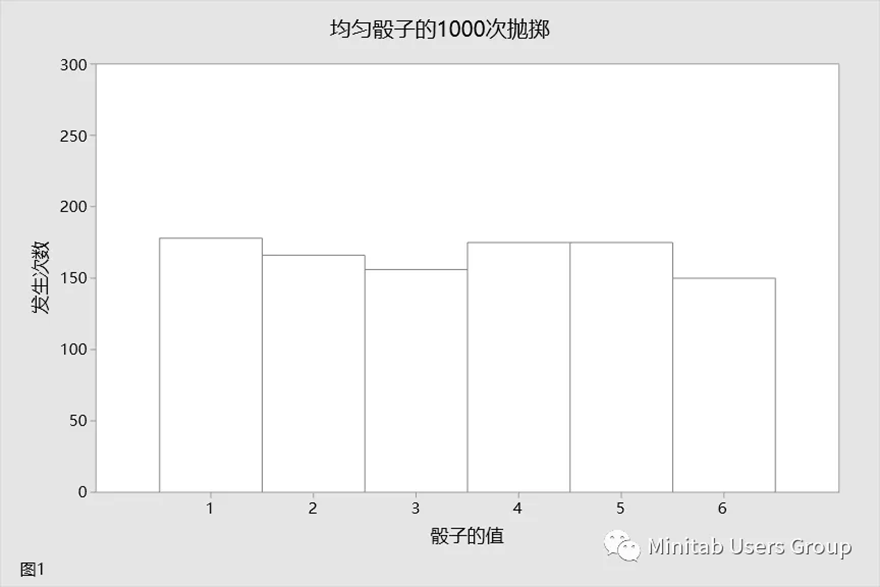
假设您掷骰子 1000 次。您希望得到相等数目的 1、2 等。让我们查看 1000 次骰子的分布(图1)。
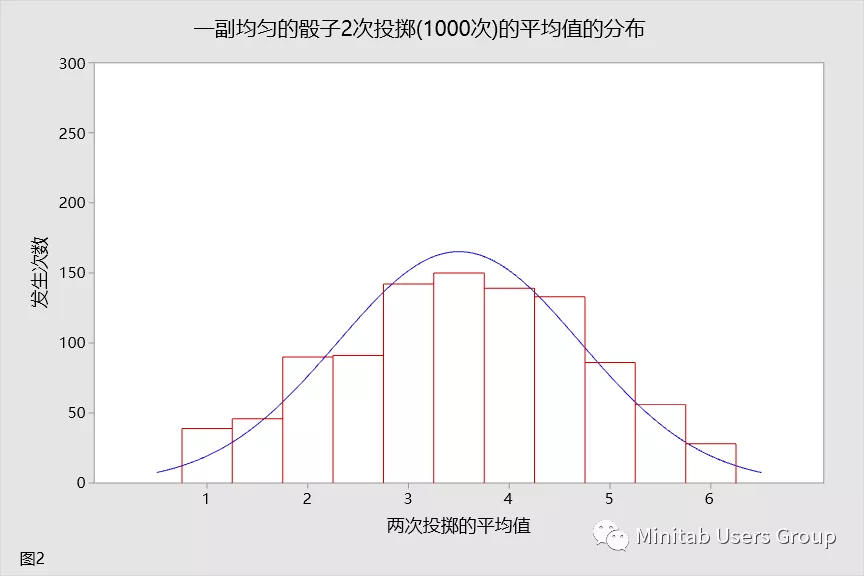
现在假设您将投掷 2 次,并采用两次投掷的平均值。您还将重复此试验 1000 次。让我们来看看两次投掷的平均值的分布。这种分布如图 2 所示。您是否注意到在只进行了两次投掷的情况下,平均值的分布已经呈现出了土堆形?
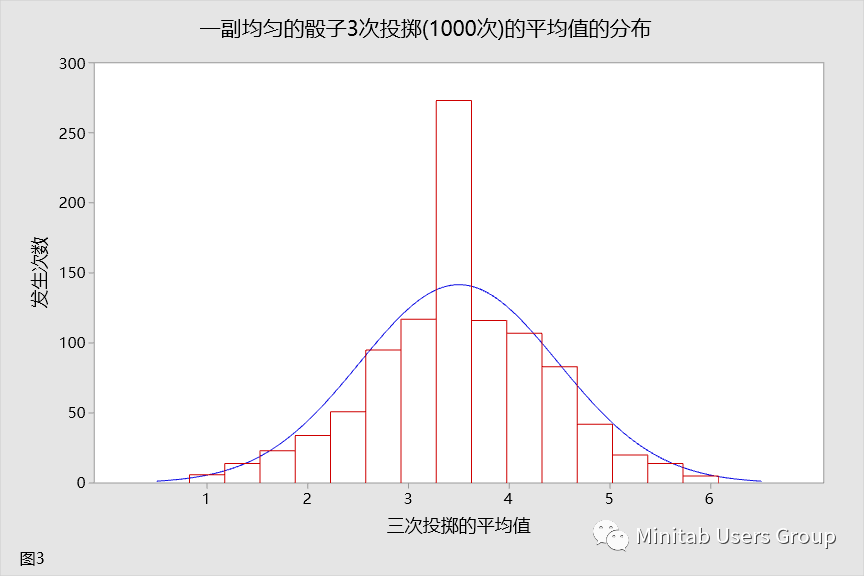
假设您现在投掷骰子三次,然后取三次投掷的平均值。再次重复此试验 1000 次。让我们来看看此举对投掷的平均值分布有何影响。这种分布如图 3 所示。同样,分布的形状与正态分布的形状相当接近。您是否注意到分布上发生了其他变化?
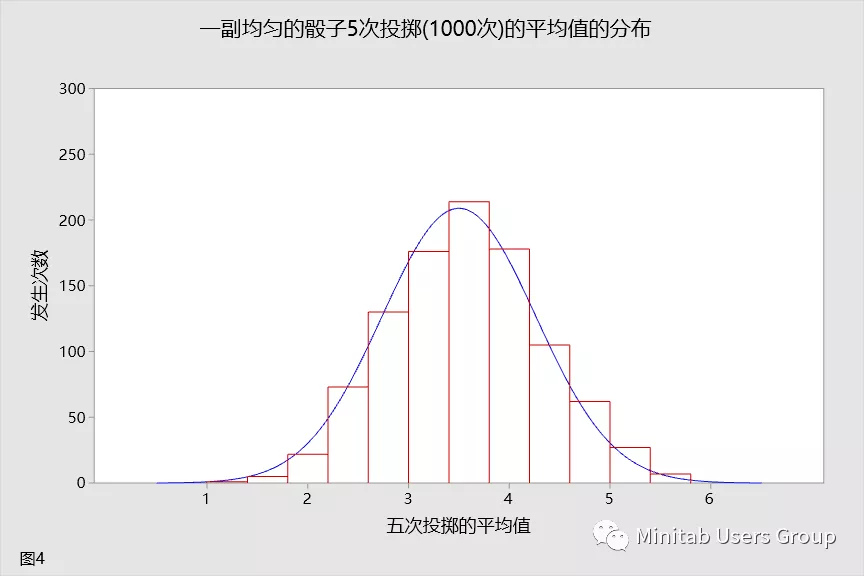
让我们投掷骰子五次,并取其平均值。再次重复此试验 1000 次。这种分布如图 4 所示。您是否已开始注意到所发生的情形中存在任何模式?
让我们继续增加平均投掷次数。此时您将投掷 10 次,并采用 10 次投掷的平均值。这种分布如图 5 所示。
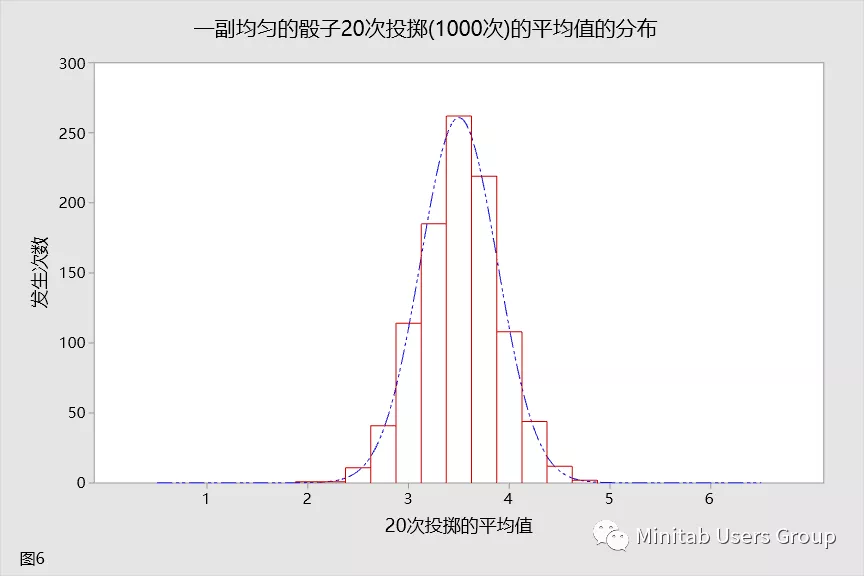
现在,随着您增加投掷次数,将看到两个现象。首先,您会看到,平均分布的形状开始与正态分布的形状相似。其次,您会看到,随着投掷次数的增加,分布变得越来越窄。让我们继续增加投掷次数。此时,您将投掷骰子 20 次。这种分布如图 6 所示。
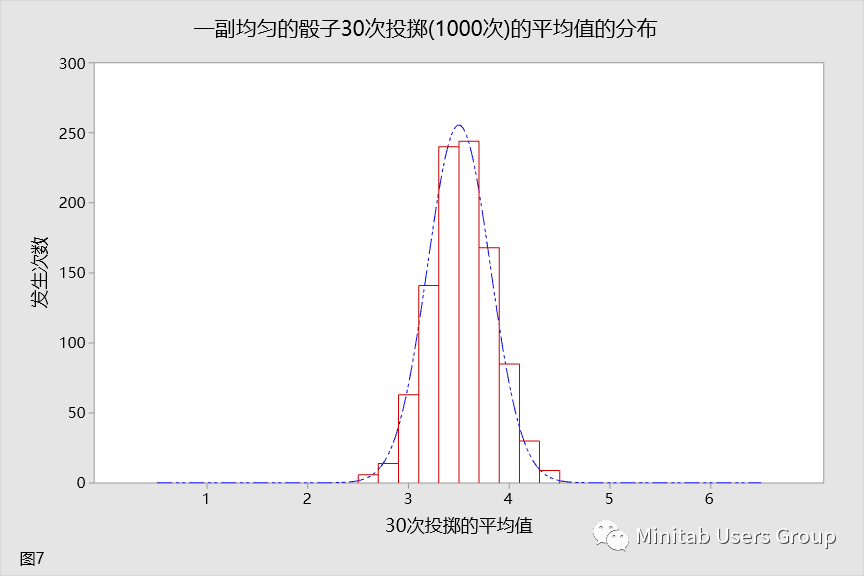
到现在,您应该确信增大样本数量对样本平均值分布是有影响的。您将再次增大样本数量,以强化这种认知。此时,您将投掷骰子 30 次。这种分布如图 7 所示。
让我们看看所呈现的情况,在一个图中绘制大小为 2、5、10、20、30 的样本的直方图,以查看变化的分布。
从上面的模拟结果,可以知道,当样本量大于30的时候,那么样本均值(取了1000次样本,得到1000个均值)的分布基本呈正态分布。
另外该定理还指出,如果根据总体不断重复绘制随机样本数量 n 以及有限均值 mu(y) 和标准差 sigma(y),然后在 n 较大时,样本均值的分布将近似呈正态分布,并且均值等于 mu(y),标准差等于 (sigma(y))/sqrt(n)。 收起阅读 »
但有些朋友,并不觉得这是一个错误的问题,甚至在他们的学习中还流传着这么一个说法:样本量大于30就可以认为是服从正态分布。当你向他问为什么的时候,会得到一个专业的解释——中心极限定理。
中心极限定理
中心极限定理(Central Limit Theorem)是统计学中最重要的结论之一。在这里,我并不想给出中心极限定理专业的定义,只需要了解它告诉我们:来自某总体的一个样本,无论该总体服从什么分布,只要样本容量足够大,其样本均值都近似服从正态分布。
请注意这里的说法:“样本均值“近似正态,而不是样本本身服从正态(不是说你抽了30个样品组成的样本数据就正态)。这里又有一个大家疑惑的地方,样本容量足够大,多大才是足够大?这个问题的答案和总体分布的形状相关,如果样本本是来自近似对称分布的总体,那么当样本量取相当小(如样本量取5)的值的时候,正态逼近的结果也会非常好。然后,如果总体的分布严重倾斜,则样本量必须取相当大的值。根据检验,对于大多数总体来说,样本容量取30或者更大,就足以得到令人满意的正态逼近结果。我想这可能就是错误认为样本量大于30就认为是正态分布的出处了。
模拟掷骰子展示中心极限定理
为了展示中心极限定理,模拟多次投掷骰子来说明。
假设您掷骰子 1000 次。您希望得到相等数目的 1、2 等。让我们查看 1000 次骰子的分布(图1)。
现在假设您将投掷 2 次,并采用两次投掷的平均值。您还将重复此试验 1000 次。让我们来看看两次投掷的平均值的分布。这种分布如图 2 所示。您是否注意到在只进行了两次投掷的情况下,平均值的分布已经呈现出了土堆形?
假设您现在投掷骰子三次,然后取三次投掷的平均值。再次重复此试验 1000 次。让我们来看看此举对投掷的平均值分布有何影响。这种分布如图 3 所示。同样,分布的形状与正态分布的形状相当接近。您是否注意到分布上发生了其他变化?
让我们投掷骰子五次,并取其平均值。再次重复此试验 1000 次。这种分布如图 4 所示。您是否已开始注意到所发生的情形中存在任何模式?
让我们继续增加平均投掷次数。此时您将投掷 10 次,并采用 10 次投掷的平均值。这种分布如图 5 所示。
现在,随着您增加投掷次数,将看到两个现象。首先,您会看到,平均分布的形状开始与正态分布的形状相似。其次,您会看到,随着投掷次数的增加,分布变得越来越窄。让我们继续增加投掷次数。此时,您将投掷骰子 20 次。这种分布如图 6 所示。
到现在,您应该确信增大样本数量对样本平均值分布是有影响的。您将再次增大样本数量,以强化这种认知。此时,您将投掷骰子 30 次。这种分布如图 7 所示。
让我们看看所呈现的情况,在一个图中绘制大小为 2、5、10、20、30 的样本的直方图,以查看变化的分布。
从上面的模拟结果,可以知道,当样本量大于30的时候,那么样本均值(取了1000次样本,得到1000个均值)的分布基本呈正态分布。
另外该定理还指出,如果根据总体不断重复绘制随机样本数量 n 以及有限均值 mu(y) 和标准差 sigma(y),然后在 n 较大时,样本均值的分布将近似呈正态分布,并且均值等于 mu(y),标准差等于 (sigma(y))/sqrt(n)。 收起阅读 »
十个常用的六西格玛统计工具及应用场景
六西格玛是一种质量改进方法,企业已经使用了几十年 - 因为它取得了成果。六西格玛项目遵循明确定义的一系列步骤,世界各国的每个行业的公司都使用这种方法来解决问题。
但是,六西格玛在很大程度上依赖于统计和数据分析,许多对质量改进不熟悉的人感到受到统计方面的威胁。你不必被吓倒。虽然数据分析确实对提高质量至关重要,但六西格玛的大多数分析并不难理解,即使您对统计数据不是很了解。但使用Minitab熟悉这些工具是一个很好的起点。本文简要介绍六西格玛中常用的10种统计工具,了解它们的作用以及它们为何如此重要。
1.帕累托图(Pareto图)
帕累托图来源于一种称为帕累托原则的观点,该观点认为大约80%的结果来自20%的原因。即使在我们的个人生活中,也很容易想到例子。例如,80%的时间你会穿买的衣服中20%的衣服,或者你在图书馆80%的时间只会听网易云音乐中收集的20%的音乐。
帕累托图可帮助您直观地了解此原则如何应用于您收集的数据。它是一种特殊类型的条形图,旨在将“少数几个”原因与“琐碎的”原因区分开来,使您能够专注于最重要的问题。例如,如果每次出现缺陷类型时就收集有关缺陷类型的数据,则帕累托图会显示哪些类型最常见,因此您可以集中精力解决最紧迫的问题。
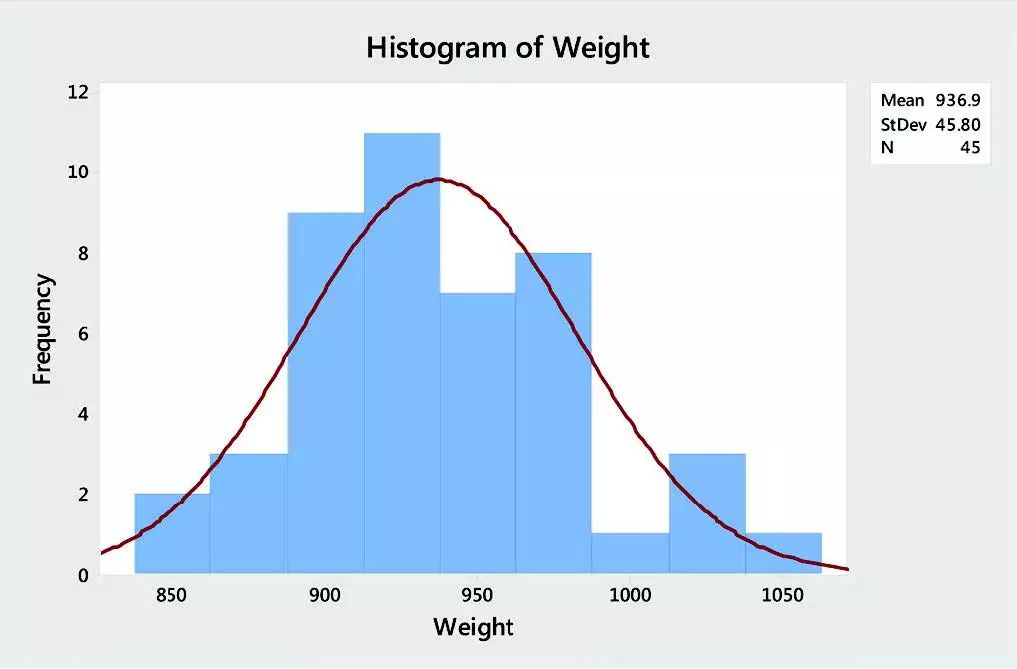
2.直方图
直方图是连续数据的图形快照。直方图使您能够快速识别数据的中心和范围。它显示了大部分数据落在哪里,以及最小值和最大值。直方图还显示您的数据是否为钟形,可以帮助您找到可能需要进一步调查的异常数据点。
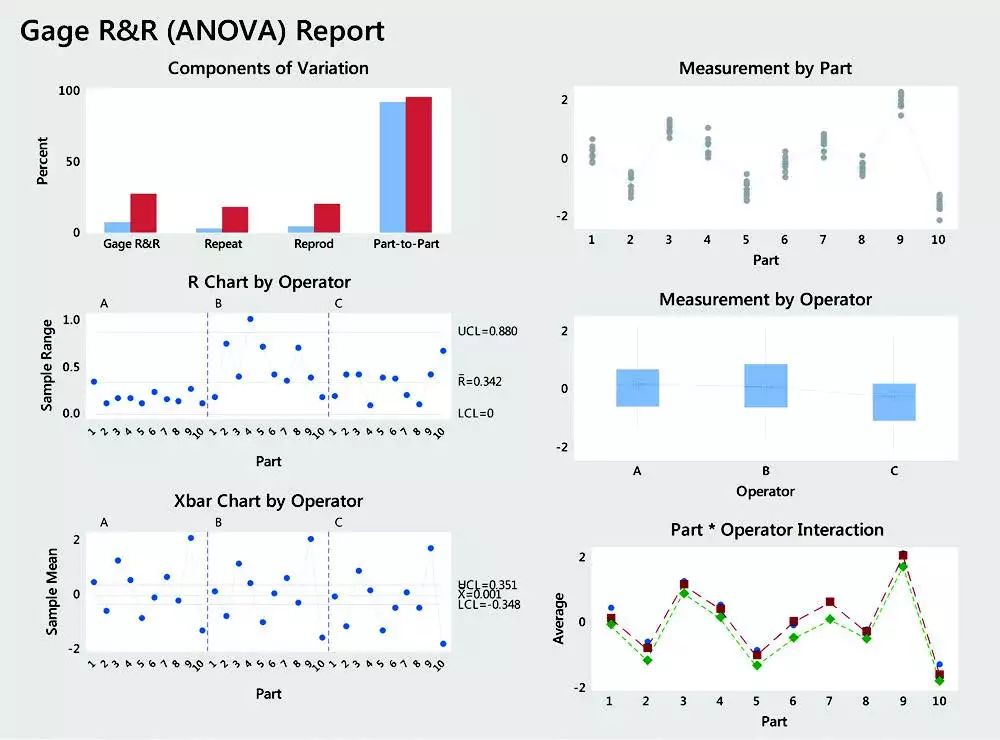
3.Gage R&R
准确的测量至关重要。你想用自己认为不可靠的数据来衡量自己吗?你会继续使用从未显示正确温度的温度计吗?如果您无法准确测量过程,则无法对其进行改进,这时Gage R&R就有了用武之地。此工具可帮助您确定连续型数值测量(如重量,直径和压力),当同一个人反复测量同一部件时,以及当不同的操作者测量相同部件时是否准确和精确。
4.属性一致性分析
另一个确保您可以信任您的数据的工具是属性一致性分析。Gage R&R评估连续型数据的重复性和再现性,而属性一致性分析评估的是属性数据,例如通过或失败。此工具显示对这些类别进行评级的人是否与已知标准,与其他评估者以及他们自己一致。
5.过程能力分析
几乎每个过程都具有可接受的下限和/或上限。例如,供应商的零件不能太大或太小,等待时间不能超过可接受的阈值,填充重量需要超过规定的最小值。能力分析向您展示您的流程与规范的完美程度,并深入了解如何改善不良流程。经常引用的能力指标包括Cpk,Ppk,Cp,Pp,百万机会缺陷数(DPMO)和西格玛水平(Z值)。
6.t检验
我们使用t检验来比较样本的平均值与目标值或另一个样本的平均值。例如,工艺参数调整后,想确定钢筋抗拉强度均值是否比原来的2000要高。如果您从两家供应商处购买调味糖浆,并想确定各自出货量的平均量是否有差异,您可以使用双样本t检验来比较两家供应商。
7.方差分析
t检验将平均值与目标进行比较,或者将两个平均值相互比较,而ANOVA(方差分析的缩写)则可以比较两个以上总体的均值。例如,ANOVA可以显示3个班次的平均产量是否相等。您还可以使用ANOVA分析多于1个变量的均值。例如,您可以同时比较3班次的均值和2个制造地点的均值。
8.回归分析
回归可帮助您确定输出与一个或多个输入因子之间是否存在关联。例如,您可以使用回归来检查公司的营销支出与其销售收入之间是否存在关联。当存在变量之间的关系时,您可以使用回归方程来描述该关系并预测给定输入值的未来输出值。
9.DOE(实验设计)
回归和ANOVA最常用于已经收集的数据。相比之下,实验设计(DOE)为您提供了一种有效的数据收集策略。它允许您同时更改或调整多个因子,以确定输入和输出之间是否存在关系。收集数据并识别重要输入后,您可以使用DOE确定每个因子的最佳设置。
10.控制图
每个过程都有一些自然的,固有的变化,但稳定(因此可预测)的过程是优质产品和服务的标志。重要的是要知道过程何时超出正常的自然变化,因为它可以指示需要解决的问题。控制图将“特殊原因”变化与可接受的自然变化区分开来。这些图表随时间变化绘制数据并标记失控数据点,因此您可以检测异常变化并在必要时采取措施。控制图还可以帮助您确保在未来持续改进流程。
小结
六西格玛可以为任何企业带来巨大的利益,但是获得这些收益需要收集和分析数据,以便您了解改进的机会并做出重大和可持续的变革。六西格玛项目的成功往往取决于在许多领域都是高技能专家的从业者,而不是统计数据。但是,通过对最常用的六西格玛统计数据和易于使用的统计软件(如Minitab)的基本了解,您可以处理与提高质量相关的统计任务,并自信地分析您的数据。 收起阅读 »
但是,六西格玛在很大程度上依赖于统计和数据分析,许多对质量改进不熟悉的人感到受到统计方面的威胁。你不必被吓倒。虽然数据分析确实对提高质量至关重要,但六西格玛的大多数分析并不难理解,即使您对统计数据不是很了解。但使用Minitab熟悉这些工具是一个很好的起点。本文简要介绍六西格玛中常用的10种统计工具,了解它们的作用以及它们为何如此重要。
1.帕累托图(Pareto图)
帕累托图来源于一种称为帕累托原则的观点,该观点认为大约80%的结果来自20%的原因。即使在我们的个人生活中,也很容易想到例子。例如,80%的时间你会穿买的衣服中20%的衣服,或者你在图书馆80%的时间只会听网易云音乐中收集的20%的音乐。
帕累托图可帮助您直观地了解此原则如何应用于您收集的数据。它是一种特殊类型的条形图,旨在将“少数几个”原因与“琐碎的”原因区分开来,使您能够专注于最重要的问题。例如,如果每次出现缺陷类型时就收集有关缺陷类型的数据,则帕累托图会显示哪些类型最常见,因此您可以集中精力解决最紧迫的问题。
2.直方图
直方图是连续数据的图形快照。直方图使您能够快速识别数据的中心和范围。它显示了大部分数据落在哪里,以及最小值和最大值。直方图还显示您的数据是否为钟形,可以帮助您找到可能需要进一步调查的异常数据点。
3.Gage R&R
准确的测量至关重要。你想用自己认为不可靠的数据来衡量自己吗?你会继续使用从未显示正确温度的温度计吗?如果您无法准确测量过程,则无法对其进行改进,这时Gage R&R就有了用武之地。此工具可帮助您确定连续型数值测量(如重量,直径和压力),当同一个人反复测量同一部件时,以及当不同的操作者测量相同部件时是否准确和精确。
4.属性一致性分析
另一个确保您可以信任您的数据的工具是属性一致性分析。Gage R&R评估连续型数据的重复性和再现性,而属性一致性分析评估的是属性数据,例如通过或失败。此工具显示对这些类别进行评级的人是否与已知标准,与其他评估者以及他们自己一致。
5.过程能力分析
几乎每个过程都具有可接受的下限和/或上限。例如,供应商的零件不能太大或太小,等待时间不能超过可接受的阈值,填充重量需要超过规定的最小值。能力分析向您展示您的流程与规范的完美程度,并深入了解如何改善不良流程。经常引用的能力指标包括Cpk,Ppk,Cp,Pp,百万机会缺陷数(DPMO)和西格玛水平(Z值)。
6.t检验
我们使用t检验来比较样本的平均值与目标值或另一个样本的平均值。例如,工艺参数调整后,想确定钢筋抗拉强度均值是否比原来的2000要高。如果您从两家供应商处购买调味糖浆,并想确定各自出货量的平均量是否有差异,您可以使用双样本t检验来比较两家供应商。
7.方差分析
t检验将平均值与目标进行比较,或者将两个平均值相互比较,而ANOVA(方差分析的缩写)则可以比较两个以上总体的均值。例如,ANOVA可以显示3个班次的平均产量是否相等。您还可以使用ANOVA分析多于1个变量的均值。例如,您可以同时比较3班次的均值和2个制造地点的均值。
8.回归分析
回归可帮助您确定输出与一个或多个输入因子之间是否存在关联。例如,您可以使用回归来检查公司的营销支出与其销售收入之间是否存在关联。当存在变量之间的关系时,您可以使用回归方程来描述该关系并预测给定输入值的未来输出值。
9.DOE(实验设计)
回归和ANOVA最常用于已经收集的数据。相比之下,实验设计(DOE)为您提供了一种有效的数据收集策略。它允许您同时更改或调整多个因子,以确定输入和输出之间是否存在关系。收集数据并识别重要输入后,您可以使用DOE确定每个因子的最佳设置。
10.控制图
每个过程都有一些自然的,固有的变化,但稳定(因此可预测)的过程是优质产品和服务的标志。重要的是要知道过程何时超出正常的自然变化,因为它可以指示需要解决的问题。控制图将“特殊原因”变化与可接受的自然变化区分开来。这些图表随时间变化绘制数据并标记失控数据点,因此您可以检测异常变化并在必要时采取措施。控制图还可以帮助您确保在未来持续改进流程。
小结
六西格玛可以为任何企业带来巨大的利益,但是获得这些收益需要收集和分析数据,以便您了解改进的机会并做出重大和可持续的变革。六西格玛项目的成功往往取决于在许多领域都是高技能专家的从业者,而不是统计数据。但是,通过对最常用的六西格玛统计数据和易于使用的统计软件(如Minitab)的基本了解,您可以处理与提高质量相关的统计任务,并自信地分析您的数据。 收起阅读 »
探索未知.预测未来------利用机器学习(CART)预测合格率
人类一直试图让机器具有智能,也就是人工智能(Artificial Intelligence)。从上世纪50年代,人工智能的发展经历了“推理期”,通过赋予机器逻辑推理能力使机器获得智能,当时的AI程序能够证明一些著名的数学定理,但由于机器缺乏知识,远不能实现真正的智能。因此,70年代,人工智能的发展进入“知识期”,即将人类的知识总结出来教给机器,使机器获得智能。 无论是“推理期”还是“知识期”,机器都是按照人类设定的规则和总结的知识运作,永远无法超越其创造者,其次人力成本太高。于是,一些学者就想到,如果机器能够自我学习问题不就迎刃而解了吗!机器学习(Machine Learning)方法应运而生,人工智能进入“机器学习时期”。机器学习的核心是“使用算法解析数据,从中学习,然后对世界上的某件事情做出决定或预测”。机器学习最大的突破是2006年的深度学习。深度学习是一类机器学习,目的是模仿人脑的思维过程,经常用于图像和语音识别。深度学习的出现导致了我们今天使用的(可能是理所当然的)许多技术。当你问你的iPhone关于今天的天气时,你的话语会用一种复杂的语音解析算法进行分析。如果没有深度学习,这一切都是不可能的。
机器学习与统计区别
机器学习是一类算法的总称,这些算法企图从大量历史数据中挖掘出其中隐含的规律,并用于预测或者分类,更具体的说,机器学习可以看作是寻找一个函数,输入是样本数据,输出是期望的结果,只是这个函数过于复杂,以至于不太方便形式化表达。
通常学习一个好的函数,分为以下三步:
1、选择一个合适的模型,这通常需要依据实际问题而定,针对不同的问题和任务需要选取恰当的模型。
2、判断一个函数的好坏,这需要确定一个衡量标准,如回归问题一般采用欧式距离,分类问题一般采用交叉验证函数。
3、找出“最好”的函数,如何从众多函数中最快的找出“最好”的那一个,学习得到“最好”的函数后,需要在新样本上进行测试,只有在新样本上表现很好,才算是一个“好”的函数。
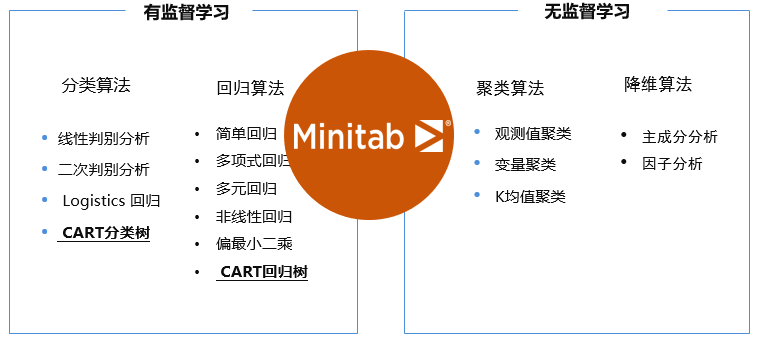
机器学习的核心是“使用算法解析数据,从中学习,然后对世界上的某件事情做出决定或预测”。这意味着,与其显式地编写程序来执行某些任务,不如教计算机如何开发一个算法来完成任务。有三种主要类型的机器学习:监督学习、非监督学习和强化学习。
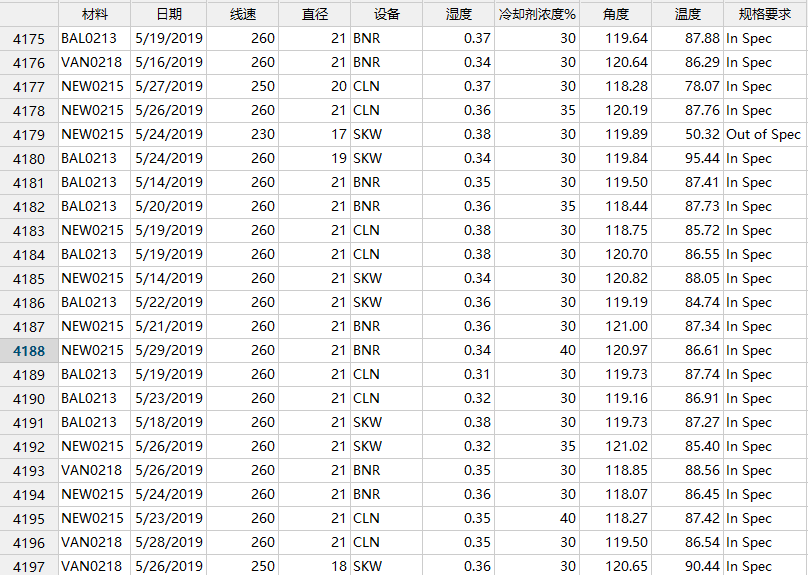
【案例分享】为了预测过程输出性能,提高客户满意度及产品质量,现从数据库中批量导入了2019年5月份生产报表,检测产品能否满足规格要求及相关生产环境,试分析影响产品质量的相关原因及预测结果。
本例共有9个变量,近5000个测试数据,其数据表如下:
在Minitab最新发布的版本Minitab19.2020中,除了可以将Python的脚本可以导入Minitab加载分析之外,还增加了机器学习的CART分析法。我们将上述案例用CART分析步骤如下:
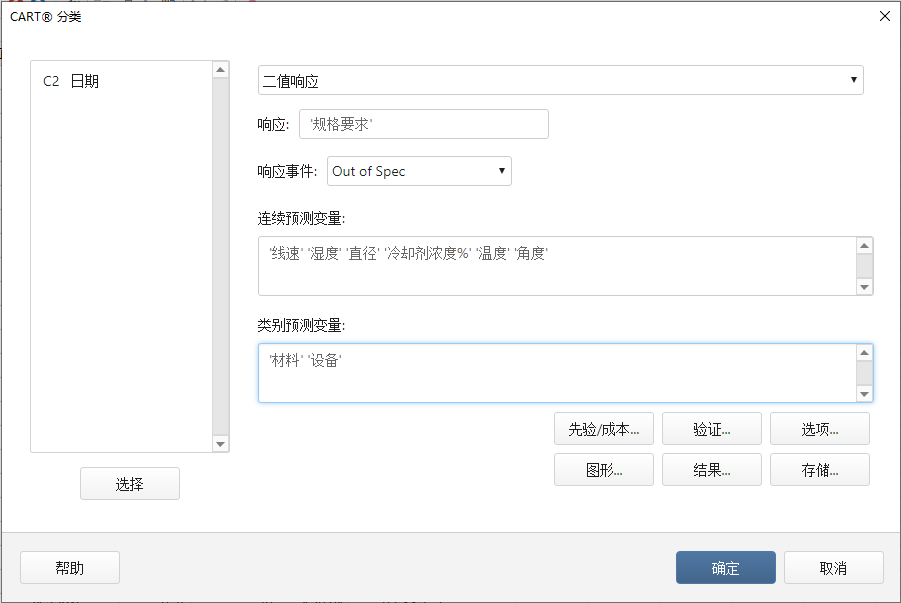
1、统计---预测分析---CART分类,将响应和影响因子分别填入对应位置
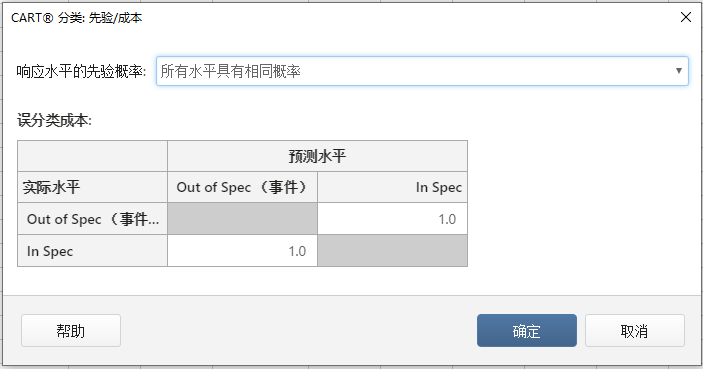
2、点击 先验/成本,设置误分类成本
误分类成本就是判断错误的风险,例如,在医学影像检测中,把健康的人误诊为病人还不是最糟的情况,只要医生能对诊断结果进行复查,并把健康的这个人找出来就可以了。但反过来,未能诊断出真正的病人而不提供给他任何治疗,则就非常危险了。默认情况下,Minitab 使用相等的成本 1。
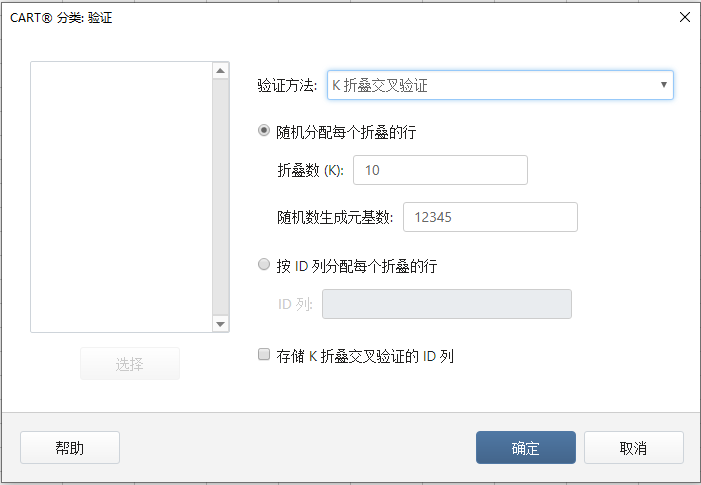
3、点击 验证,选择验证方法
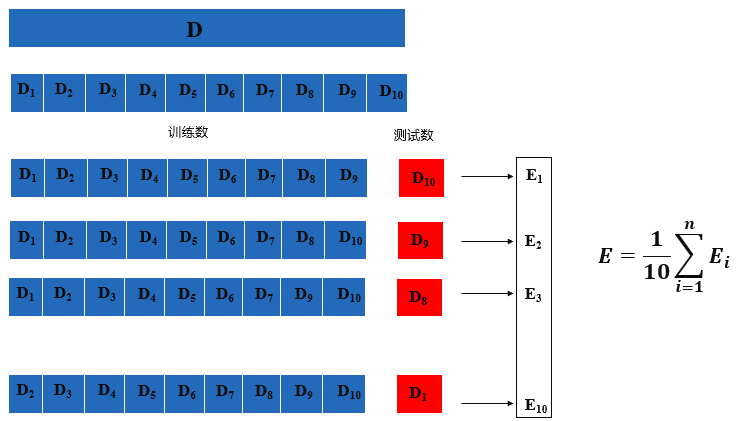
设置模型验证:数据通常被分为训练数据和测试数据
训练数据(学习数据)通常被用来创建模型及评估模型的系数;测试数据通常检模型性能,通过测试数据得到拟合值,在用训练数据的数据和对应的拟合值进行比较来检验模型的预测性能通过验证,防止模型过度拟合若用同一组数据来拟合模型并评估模型的拟合优度,会导致过度拟合,过度拟合的模型并不能用于很好的预测…..
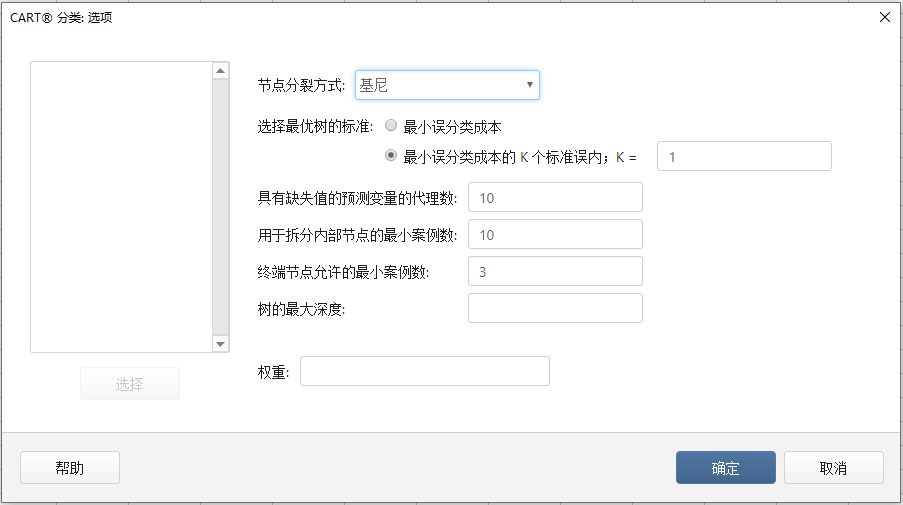
4、点击 选项,设置节点分裂方式
默认的节点分裂,选择 基尼
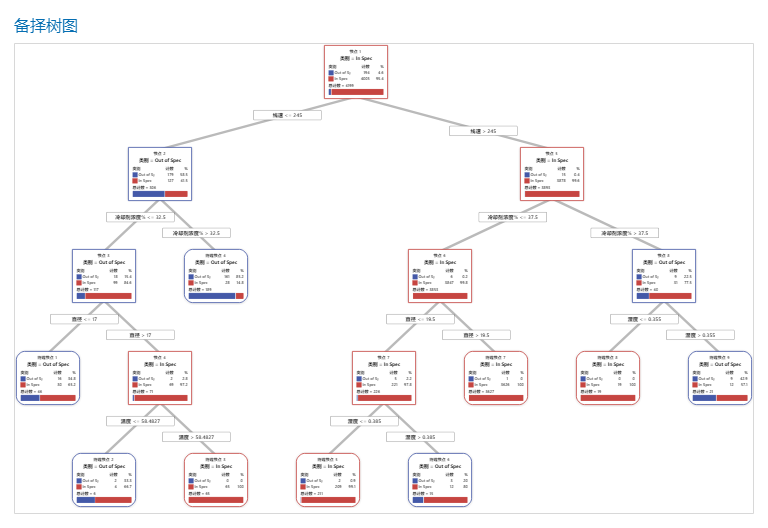
对所有对话框点击 确定,查看Minitab输出(部分):
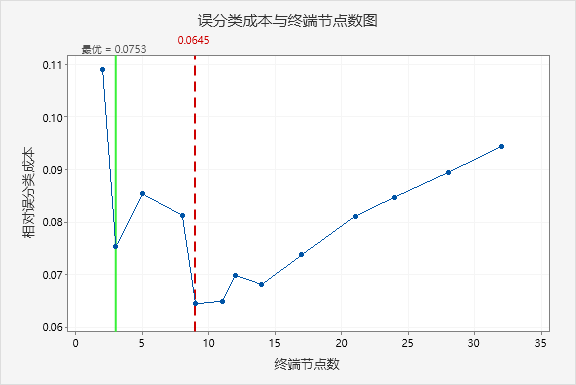
默认情况下,Minitab 为误分类成本在最小误分类成本 1 个标准误内的最小树生成输出。也可以识别最优树的序列中探索其他树。终端节点数越多,模型就越复杂。
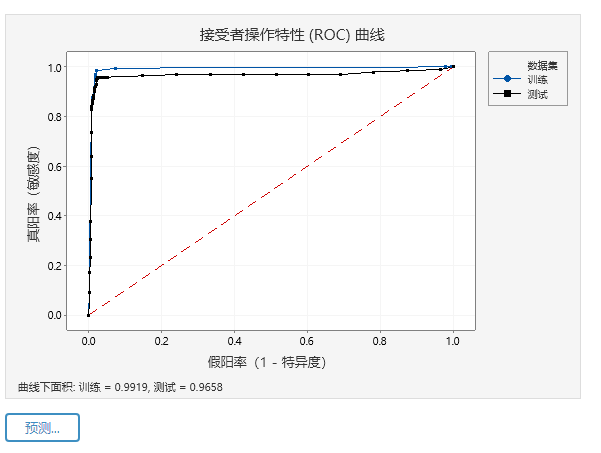
ROC曲线指受试者工作特征曲线 / 接收器操作特性曲线(receiver operating characteristic curve), 是反映敏感性和特异性连续变量的综合指标,是用构图法揭示敏感性和特异性的相互关系,它通过将连续变量设定出多个不同的临界值,从而计算出一系列敏感性和特异性,再以敏感性为纵坐标、(1-特异性)为横坐标绘制成曲线,曲线下面积越大,诊断准确性越高。
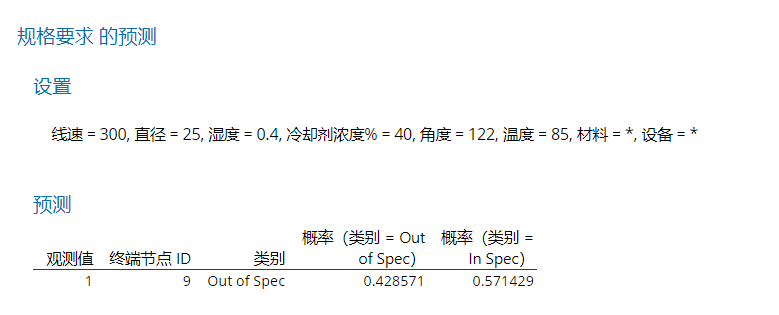
点击ROC图左下角的预测,可以根据模型预测不同场景下的输出概率。
总结:
机器学习是目前业界最为火热的一项技术,从网上的每一次淘宝的购买东西,到自动驾驶汽车技术,以及网络攻击抵御系统等等,都有机器学习的因子在内,同时机器学习也是最有可能使人类完成“AI 梦”的一项技术,各种人工智能目前的应用,如微软小冰聊天机器人,到计算机视觉技术的进步,都有机器学习努力的成分。作为全球领先的统计分析软件,Minitab在2018年收购了SPM,并在Minitab.19.2020版中增加了预测分析的CART分类和CART回归功能,能够帮助我们了解一些机器学习的相关知识与概念,更好的理解为我们带来莫大便利技术的背后原理,以及让我们更好的理解当代科技的进程。 收起阅读 »
田口设计案例-晶体外延层生长实验
案例背景
生产集成电路(IC)器件的一个初始步骤是在抛光的硅晶片上产生一个外延层,镶在一个称为感应器的六面柱体上(每面有两块晶片),这个六面柱体在一个钟形容器里旋转,这个容器通过其顶部的喷咀喷入化学蒸汽并加热。这个过程持续到外延层生长到所要求的厚度,厚度的目标值14.5微米(um),其误差范围为14.5土0.5微米,即实际的厚度应该尽可能接近14.5,并在区间[14,15]内。当前的设置造成的偏差超过了指定的1.0微米,于是试验人员需要找出可以设置的过程因子使得外延层的不均匀性达到最小,同时确保平均厚度尽可能接近目标值。
稳健参数设计
响应变差可以通过减小噪声变差来减小,但这可能要付出高的经济代价。由Genichi Taguchi最先提出的稳健参数设计(robust parameter design)是一种可选择的策略,该策略是通过探索控制因子与噪声因子间的交互效应来改变控制因子的水平组合来减小响应变差。因为控制因子通常很易于改变,所以稳健参数设计比直接减小噪声变差更经济更方便。
外延层生长试验的因子和水平
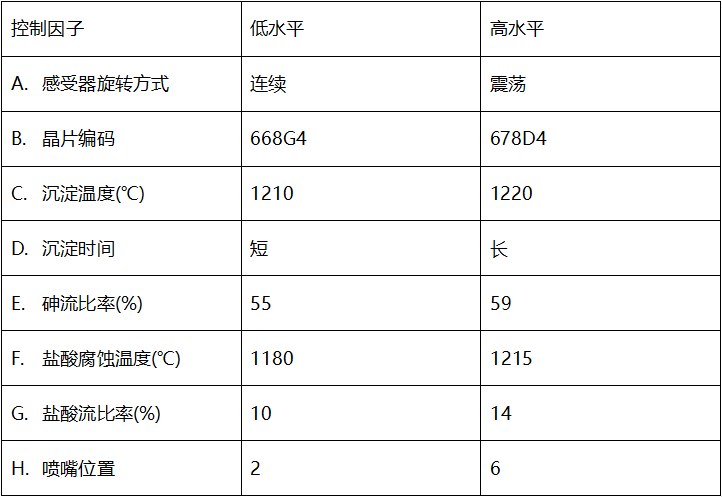
原始外延层生长试验的试验因子如下表所示,共有八个控制因子(A-H)和两个噪声因子(L和M)。
每个感受器有四个面,因此因子M有四水平。在每一个面上位置幽分顶部和底部(因子L)。在最初的试验中, Kackar and Shoemaber (1986)报告六个面的结果.为了方便说明,这里我们只考虑四个面。因为所期望的是在任何面和位置上都有均匀的厚度,所以因子L和M都处理为噪声因子。
厚度的目标值是14.5微米,规定误差限制在14.5士0.5微米。这样,试验的目标就是在保持14.5微米的平均厚度的同时,最小化外延层在四个面以及顶、底部上厚度的不均匀性。
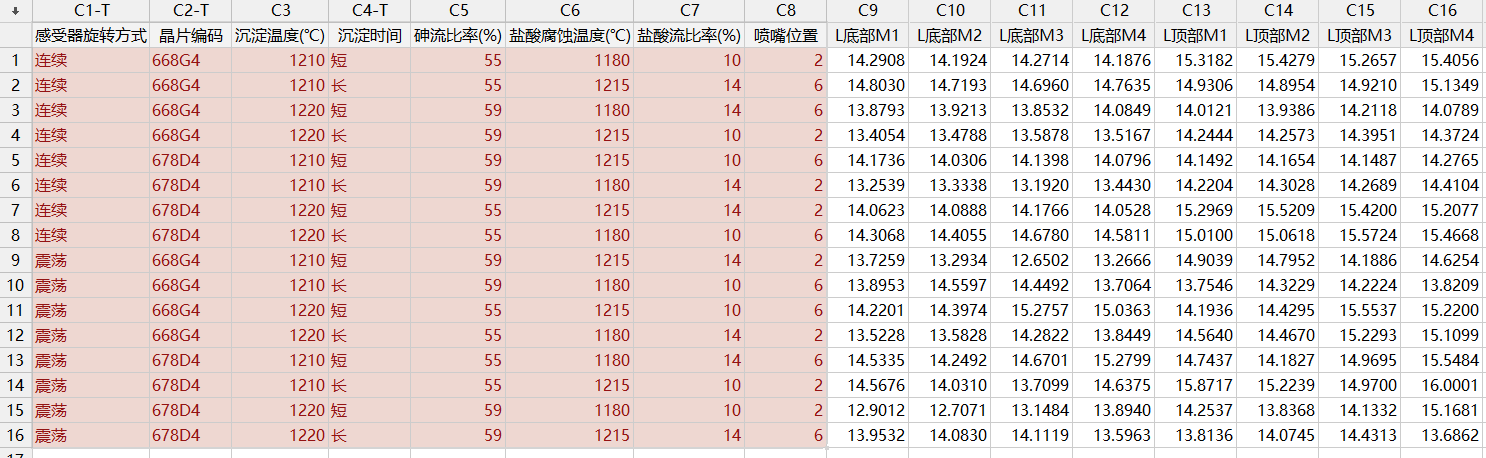
乘积表分析
此田口设计的内表采用L16 (2^8)的正交表(表示设计有16个实验和8个因子,以及 每个因子2个水平)。外表对两个噪声因子选用了2x4设计,这样每个控制因子水平组合就有8个观测值。那么,按照乘积表分析的话就有16x8=128次实验。
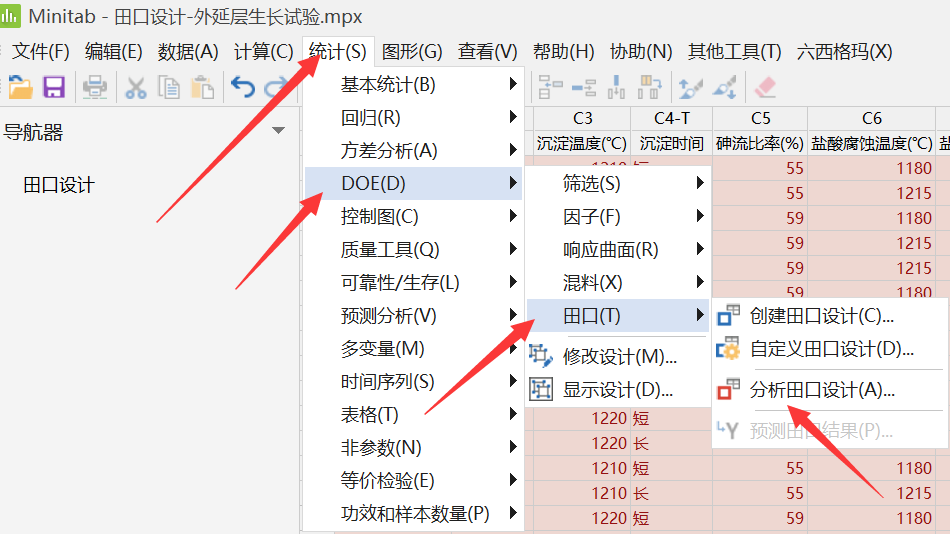
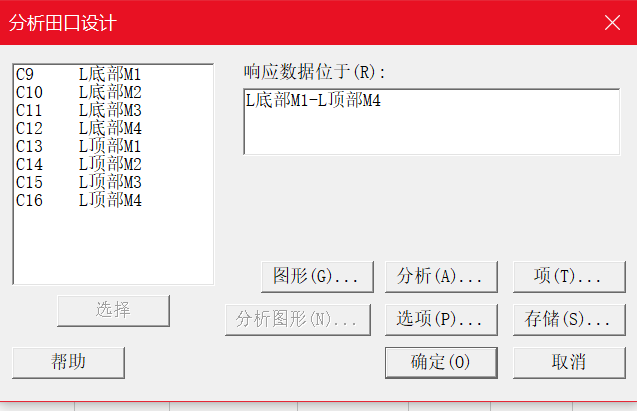
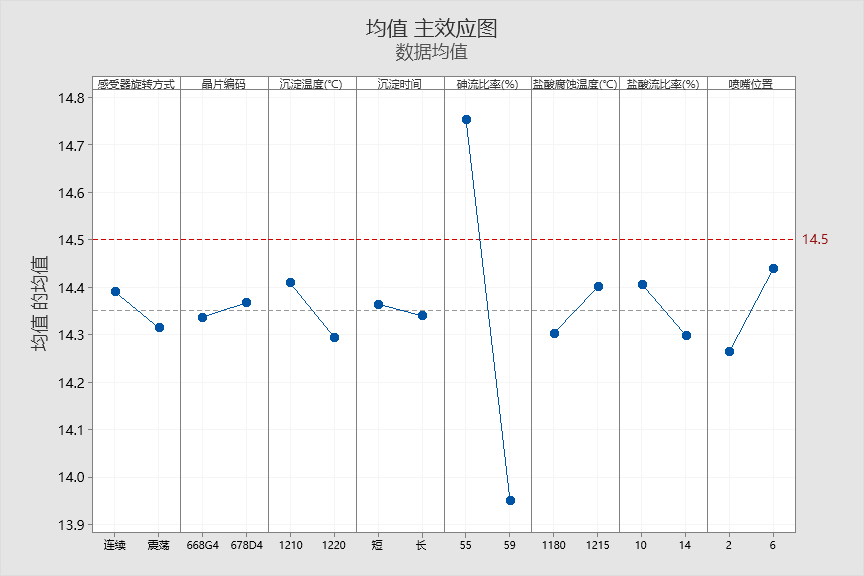
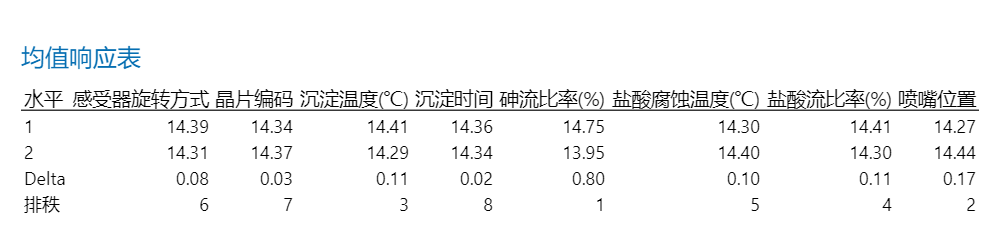
Minitab中田口分析
望目特征问题的两步程序:
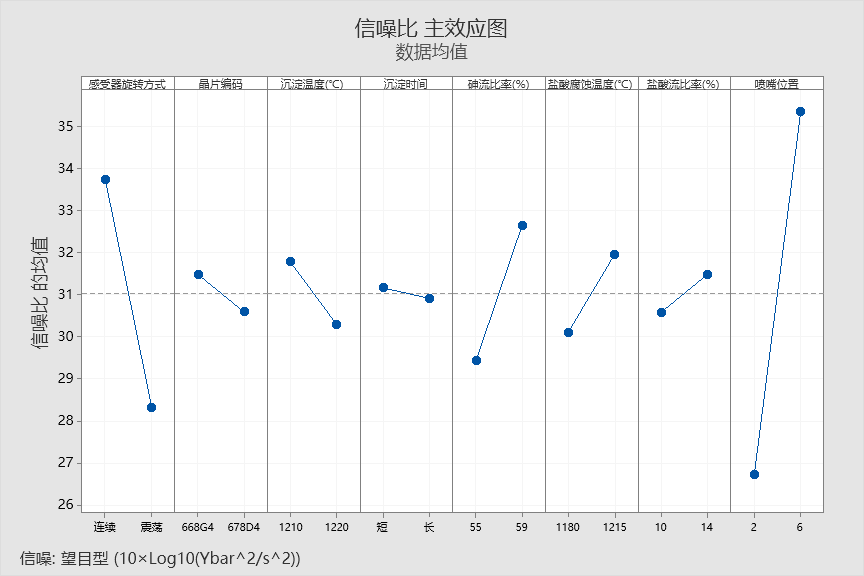
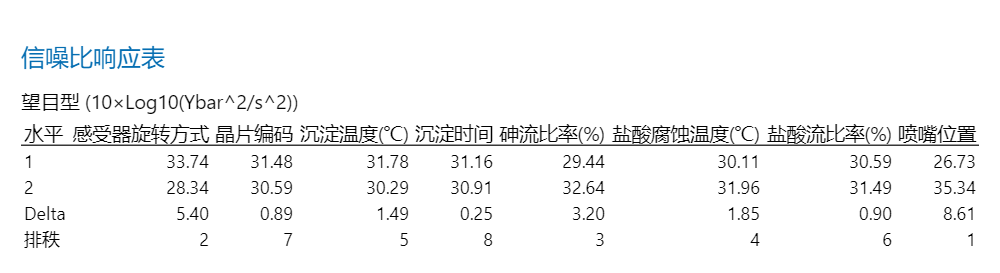
选择散度因子的水平使散度最小化(信噪比最大化)
选择调节因子的水平使位置达到目标值
要想第一步中信噪比最大化,则应该取因子组合为:
A1B1C1D1E2F2G2H2
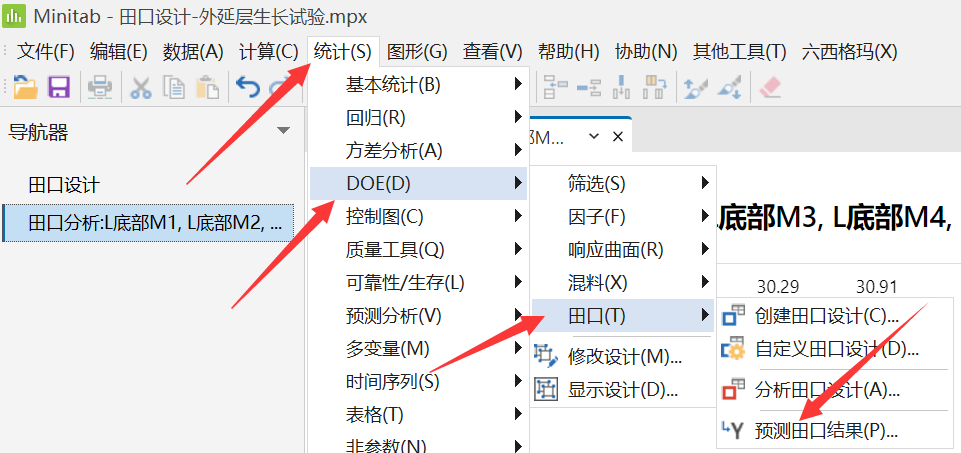
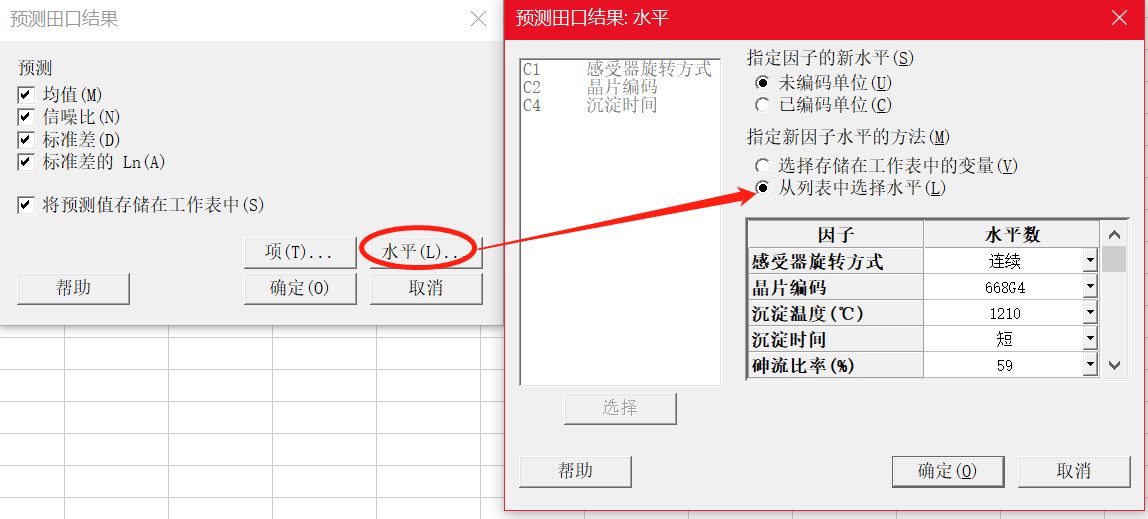
基于以上最佳信噪比组合,预测均值是否达到目标值14.5微米。
由以上预测结果可知,均值没有达到14.5微米,需要进行调节。
从下面的均值主效应图中可以发现,砷流比率(%)是一个合适的调节因子。
为此,我们固定A1B1C1D1F2G2H2,改变E的水平进行预测,结果如下:
根据预测的结果,我们下一步将会固定A1B1C1D1F2G2H2,因子E砷流比率(%)在(55,59)范围内选取,再次进行新的实验。
思考
在本案例中为了实现稳健参数设计,我们用的是田口设计中的乘积表,但乘积表实验次数太多了(128次),有没有其他方法也可以实现稳健参数设计呢?另外,乘积表分析除了实验次数多以外,还有没有其他一些缺点呢? 收起阅读 »
生产集成电路(IC)器件的一个初始步骤是在抛光的硅晶片上产生一个外延层,镶在一个称为感应器的六面柱体上(每面有两块晶片),这个六面柱体在一个钟形容器里旋转,这个容器通过其顶部的喷咀喷入化学蒸汽并加热。这个过程持续到外延层生长到所要求的厚度,厚度的目标值14.5微米(um),其误差范围为14.5土0.5微米,即实际的厚度应该尽可能接近14.5,并在区间[14,15]内。当前的设置造成的偏差超过了指定的1.0微米,于是试验人员需要找出可以设置的过程因子使得外延层的不均匀性达到最小,同时确保平均厚度尽可能接近目标值。
稳健参数设计
响应变差可以通过减小噪声变差来减小,但这可能要付出高的经济代价。由Genichi Taguchi最先提出的稳健参数设计(robust parameter design)是一种可选择的策略,该策略是通过探索控制因子与噪声因子间的交互效应来改变控制因子的水平组合来减小响应变差。因为控制因子通常很易于改变,所以稳健参数设计比直接减小噪声变差更经济更方便。
外延层生长试验的因子和水平
原始外延层生长试验的试验因子如下表所示,共有八个控制因子(A-H)和两个噪声因子(L和M)。
每个感受器有四个面,因此因子M有四水平。在每一个面上位置幽分顶部和底部(因子L)。在最初的试验中, Kackar and Shoemaber (1986)报告六个面的结果.为了方便说明,这里我们只考虑四个面。因为所期望的是在任何面和位置上都有均匀的厚度,所以因子L和M都处理为噪声因子。
厚度的目标值是14.5微米,规定误差限制在14.5士0.5微米。这样,试验的目标就是在保持14.5微米的平均厚度的同时,最小化外延层在四个面以及顶、底部上厚度的不均匀性。
乘积表分析
此田口设计的内表采用L16 (2^8)的正交表(表示设计有16个实验和8个因子,以及 每个因子2个水平)。外表对两个噪声因子选用了2x4设计,这样每个控制因子水平组合就有8个观测值。那么,按照乘积表分析的话就有16x8=128次实验。
Minitab中田口分析
望目特征问题的两步程序:
选择散度因子的水平使散度最小化(信噪比最大化)
选择调节因子的水平使位置达到目标值
要想第一步中信噪比最大化,则应该取因子组合为:
A1B1C1D1E2F2G2H2
基于以上最佳信噪比组合,预测均值是否达到目标值14.5微米。
由以上预测结果可知,均值没有达到14.5微米,需要进行调节。
从下面的均值主效应图中可以发现,砷流比率(%)是一个合适的调节因子。
为此,我们固定A1B1C1D1F2G2H2,改变E的水平进行预测,结果如下:
根据预测的结果,我们下一步将会固定A1B1C1D1F2G2H2,因子E砷流比率(%)在(55,59)范围内选取,再次进行新的实验。
思考
在本案例中为了实现稳健参数设计,我们用的是田口设计中的乘积表,但乘积表实验次数太多了(128次),有没有其他方法也可以实现稳健参数设计呢?另外,乘积表分析除了实验次数多以外,还有没有其他一些缺点呢? 收起阅读 »
过程能力分析04—非正态(非参数方法)
通过此系列文章,目前我们学习了过程能力分析的意义,基于Minitab的正态/非正态数据过程能力分析的思路和方法,其中在非正态数据能力分析中,我们讲了两种方法——转换方法和拟合其他分布方法。文章发布后,果不其然大家又有了新的问题,我们今天先来回答一些问题,再来介绍非正态数据能力分析的另外一种方法——非参数方法。
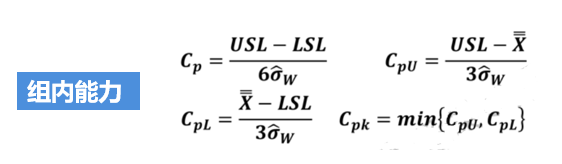
你有这些疑问吗?
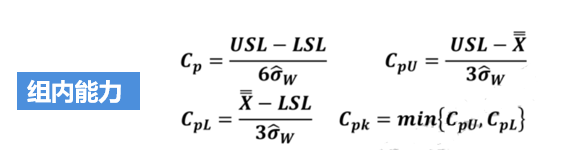
基于前面文章的说明,我们反复强调过程能力分析的一些前提条件(计算Cp/Cpk要求数据满足“独立、正态、MSA合格、稳定”,计算Pp/Ppk只要求数据满足“MSA合格,独立”)。我们还说过,以下公式只适用于正态分布数据。
那么,你有跟下面这位朋友一样的疑问吗?
对于这个问题,首先我们要知道,不管是正态数据还是非正态数据都可以计算Ppk,但是拟合分布不同计算结果肯定是有差异。如果数据正态可以按照上面的公式计算,如果非正态我们前面文章介绍了两种方法——转换/拟合其他分布。虽然计算Ppk不需要数据正态,但是做为数据分析人员我们要知道到底选择的正态方法还是非正态方法。直白点说,虽然计算Ppk不要求数据正态,但是我们仍然要在做过程能力分析计算Ppk之前执行正态性检验,只有这样你才知道从Minitab的哪个窗口进入分析。
另外一个问题,也是经常被问到(就我而言,就最少被问过不下20次)。
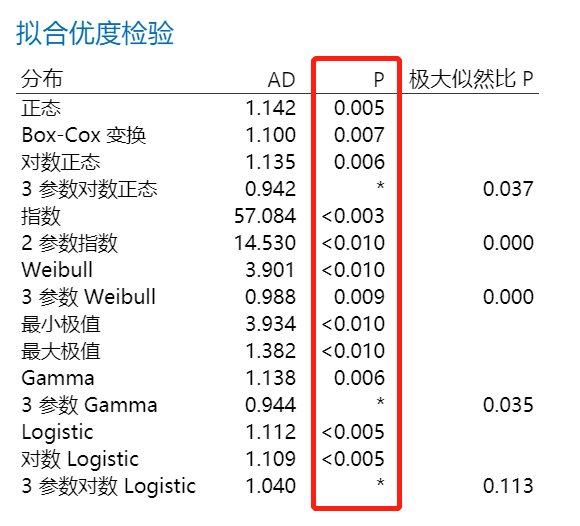
前面文章我们说过,如果数据非正态不要急着转换数据或盲目套其他分布,我们可以先来个“个体分布标识”。但是在“个体分布标识”中我们可能会遇到以下情况——两种变换都不行,14种分布中没有一个能够很好拟合数据。
对于这种情况,我们需要花费更多的精力回到数据搜集的现场做调查,而不是为了得到一个过程能力报告去寻求统计专家的帮助(再高明的专家如果不去现场也只能帮助你猜原因)。
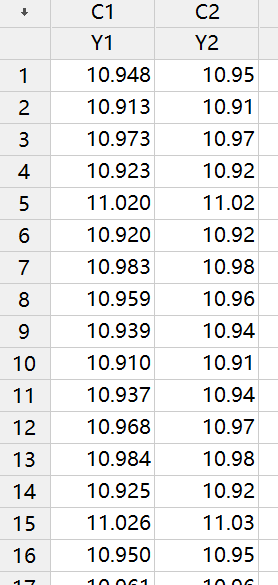
比如像上面的“个体分布标识”输出,为什么找不到合适分布,其实我把数据展示一部分给大家看一下就知道原因了(测量系统分辨力不够或数据经过了修约处理)。
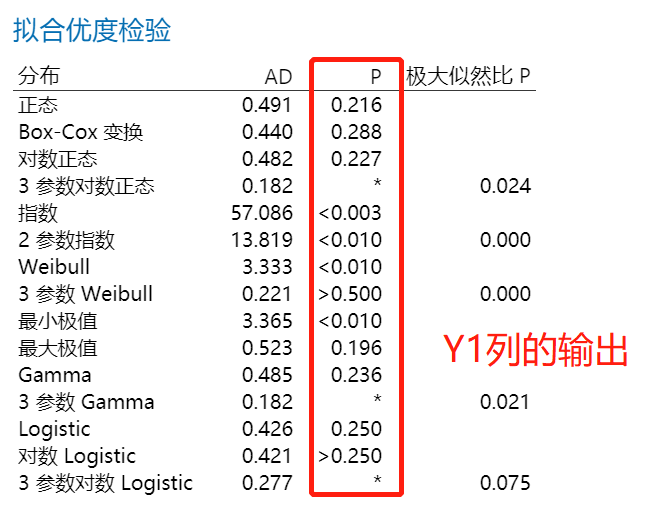
上面的“个体分布标识”是Y2的输出结果,如果我对Y1列执行相同分析呢?
这里我只是展示一种可能找不到合适分布的原因——测量系统分辨力不足,那你的数据又是什么原因导致找不到合格分布呢?这个问题别人无法回答,需要你去现场找答案。那如果我所有怀疑的原因都找了一圈结果还是没有发现问题出在哪里,那可不可以计算过程能力呢?这时候如果你的数据量比较大的话(最好1000以上),我们还有一种方法可以来计算过程能力——非参数方法。这种方法不需要知道拟合分布,但要求样本量比较大。
非参数方法
非参数方法计算过程能力的核心逻辑跟前面介绍的拟合其他分布是一样的。
因为找不到合适拟合分布,所以这里的分位数计算就不能用之前的方法了,在这里你可以手算也可以利用 Minitab自带的宏命令来计算这些分位数。
点击“帮助”菜单,我们可以在帮助文档中找到相应的宏命令。
把这个宏命令下载下来,运行之前请阅读仔细阅读帮助中说明,尤其要注意把宏放到指定的位置。 收起阅读 »
你有这些疑问吗?
基于前面文章的说明,我们反复强调过程能力分析的一些前提条件(计算Cp/Cpk要求数据满足“独立、正态、MSA合格、稳定”,计算Pp/Ppk只要求数据满足“MSA合格,独立”)。我们还说过,以下公式只适用于正态分布数据。
那么,你有跟下面这位朋友一样的疑问吗?
对于这个问题,首先我们要知道,不管是正态数据还是非正态数据都可以计算Ppk,但是拟合分布不同计算结果肯定是有差异。如果数据正态可以按照上面的公式计算,如果非正态我们前面文章介绍了两种方法——转换/拟合其他分布。虽然计算Ppk不需要数据正态,但是做为数据分析人员我们要知道到底选择的正态方法还是非正态方法。直白点说,虽然计算Ppk不要求数据正态,但是我们仍然要在做过程能力分析计算Ppk之前执行正态性检验,只有这样你才知道从Minitab的哪个窗口进入分析。
另外一个问题,也是经常被问到(就我而言,就最少被问过不下20次)。
前面文章我们说过,如果数据非正态不要急着转换数据或盲目套其他分布,我们可以先来个“个体分布标识”。但是在“个体分布标识”中我们可能会遇到以下情况——两种变换都不行,14种分布中没有一个能够很好拟合数据。
对于这种情况,我们需要花费更多的精力回到数据搜集的现场做调查,而不是为了得到一个过程能力报告去寻求统计专家的帮助(再高明的专家如果不去现场也只能帮助你猜原因)。
比如像上面的“个体分布标识”输出,为什么找不到合适分布,其实我把数据展示一部分给大家看一下就知道原因了(测量系统分辨力不够或数据经过了修约处理)。
上面的“个体分布标识”是Y2的输出结果,如果我对Y1列执行相同分析呢?
这里我只是展示一种可能找不到合适分布的原因——测量系统分辨力不足,那你的数据又是什么原因导致找不到合格分布呢?这个问题别人无法回答,需要你去现场找答案。那如果我所有怀疑的原因都找了一圈结果还是没有发现问题出在哪里,那可不可以计算过程能力呢?这时候如果你的数据量比较大的话(最好1000以上),我们还有一种方法可以来计算过程能力——非参数方法。这种方法不需要知道拟合分布,但要求样本量比较大。
非参数方法
非参数方法计算过程能力的核心逻辑跟前面介绍的拟合其他分布是一样的。
因为找不到合适拟合分布,所以这里的分位数计算就不能用之前的方法了,在这里你可以手算也可以利用 Minitab自带的宏命令来计算这些分位数。
点击“帮助”菜单,我们可以在帮助文档中找到相应的宏命令。
把这个宏命令下载下来,运行之前请阅读仔细阅读帮助中说明,尤其要注意把宏放到指定的位置。 收起阅读 »
过程能力分析03—非正态(拟合其他分布法)
对于过程能力分析,通过之前的文章我们知道在计算能力指标之前需要确认一些前提条件是否满足要求(独立,正态,MSA合格,稳定),今天我们继续延续之前的话题来讨论非正态数据如何做过程能力分析。
非正态解决方案
如果您使用为正态数据设计的能力分析,您的数据必须服从正态分布。
对于上面的这些公式,我相信很多朋友比较熟悉(不同教材在公式写法和叫法上可能稍微不同),但我们今天讨论的不是这组公式,为什么呢?因为上面这些公式只适用于正态数据,而我们今天想分享的是非正态数据的能力分析。
对于非正态数据,我们可以通过以下方法来获得准确描述生成非正态数据的过程的能力指数。
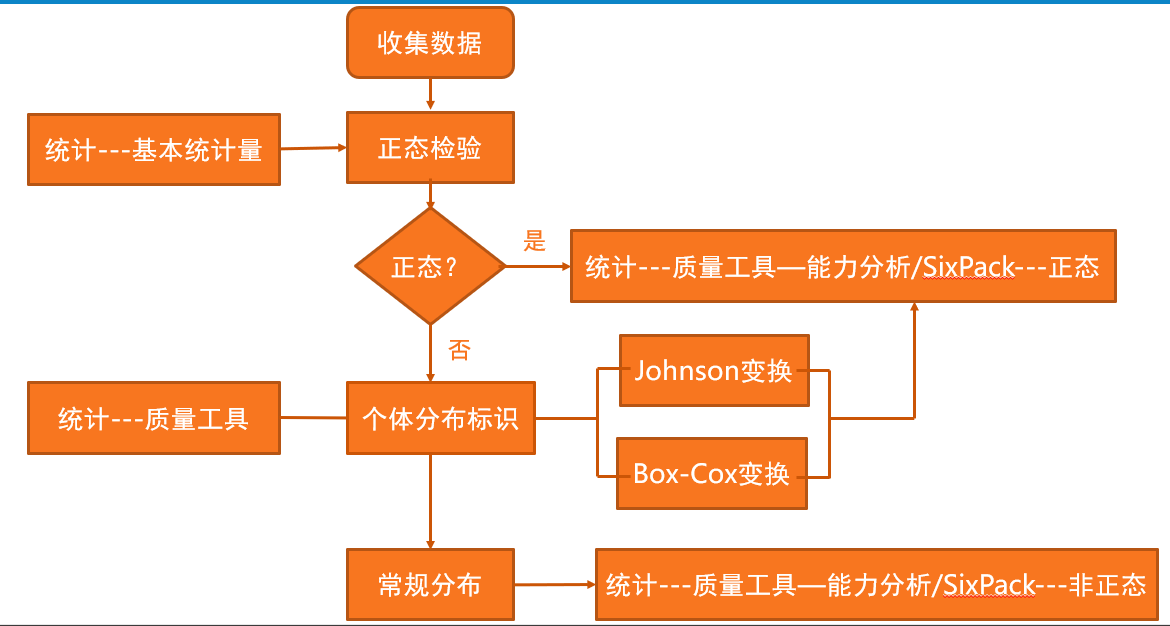
正如你所看到的,解决方法有很多,当然方法选择不同结果肯定是有差异的,那么问题又来了,哪个方法是比较合适的呢?别急,我们可以先参考以下路径图帮助我们选择。
在上一篇文章中我们分享了变换的方法(Box-Cox变换),在这篇文章中,我们打算找到拟合数据的合适分布(除了正态分布外,Minitab在这里还提供了其他13种分布),采用非正态的方法来计算Ppk(注意,由于是非正态分布,这时候就无法计算Cp/CpK了)。
拟合其他分布法(ISO方法)原理
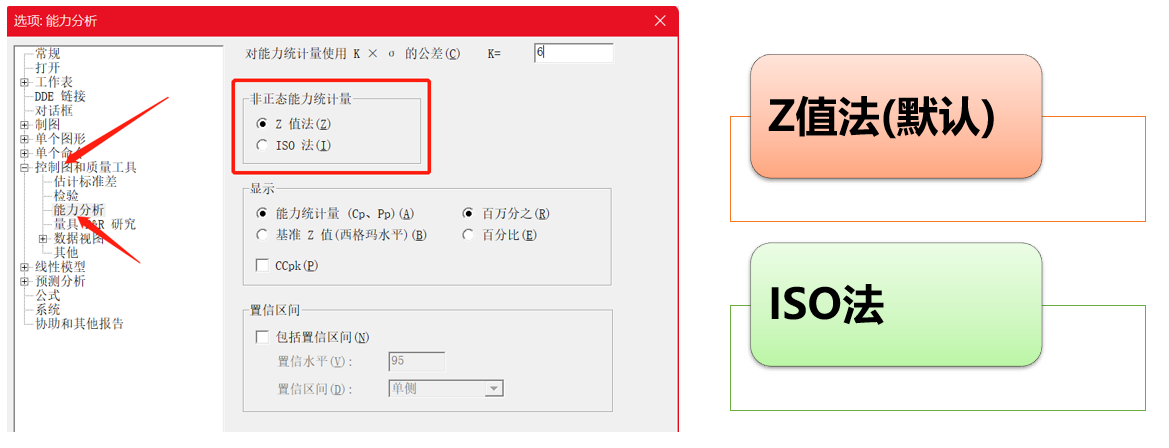
对于非正态数据,Minitab后台提供两种算法(21版本中,默认算法为“Z值法”)
但是,我们今天要分享的是“ISO方法”,原因很简单,这种算法大家在六西格玛相关课程和教材中其实学过了(先混个脸熟)。
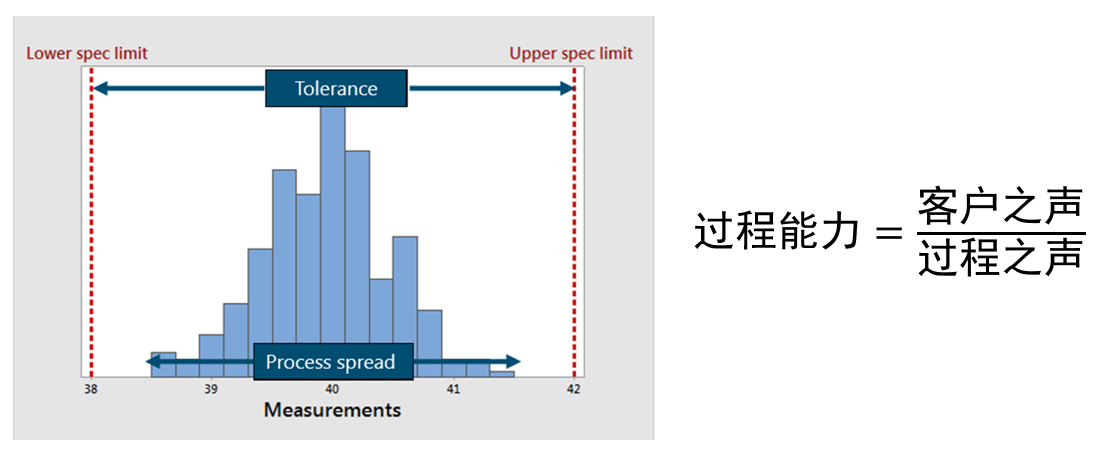
介绍“ISO方法”之前,我们首先来回顾一下能力分析的含义(如下图所示)。
其中,“客户之声”就是客户给定的公差带宽(USL-LSL),关键是怎么得到“过程之声”。
回想一下,如果数据服从正态分布,我们是怎么估计“过程之声”的?用正态分布的均值做为中心位置,用平均值±3标准差来构造一个99.73%的区间来做为“过程之声”的估计。
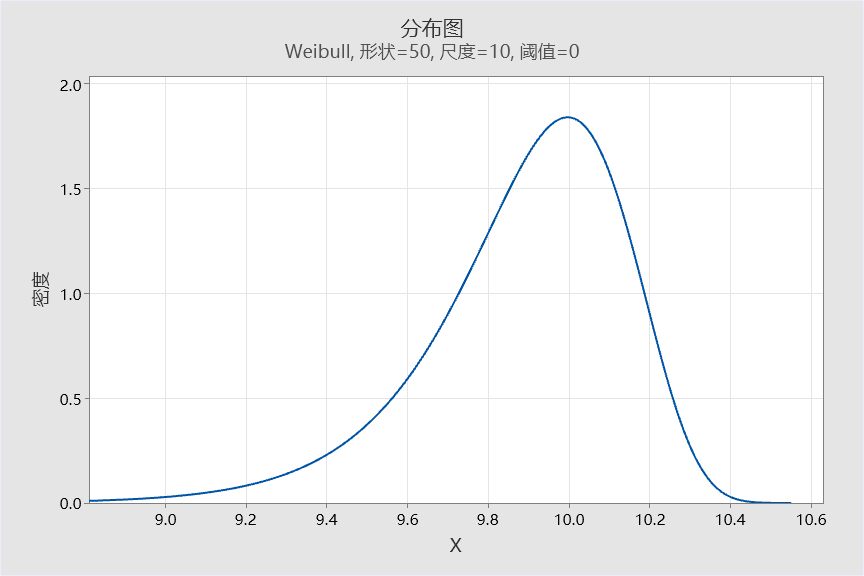
那如果是非正态数据呢,我们是不是也可以想办法来获得“过程之声”?但是很多非正态数据的分布不像正态分布那样是对称的(如下面的Weibull分布)。
那么这时候怎么获得中心位置和99.73%的区间呢?我们可以借助“ISO算法”通过计算分位数方法来估计“过程之声”。
说明:
表示指定分布的第0.99865个百分位数(太专业了,看不懂?直白一点说,分布选择不同,计算出来的结果不一样,所以我们需要找到合适的分布)。说到这里我相信大家应该理解了为什么在用Minitab做非正态数据能力分析时需要我们先指定分布了。
拟合其他分布法(ISO方法)计算
基于以上分析,我们可以通过以下三步骤来计算非正态数据的过程能力。
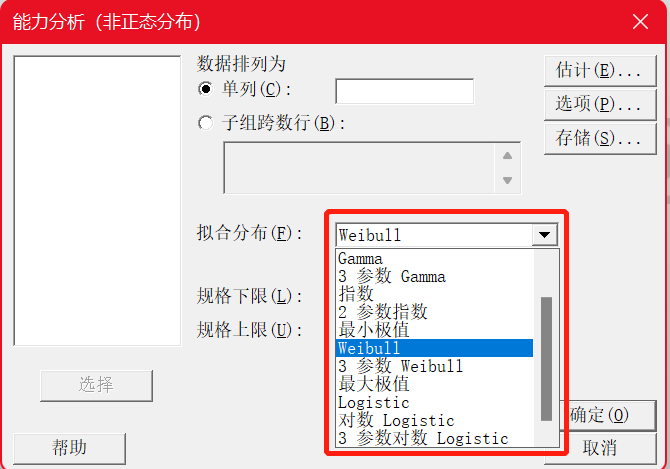
找到合适的分布(除正态分布外有13种选择),怎么确定哪种分布拟合的比较好呢?我们可以利用Minitab中的“个体分布标识”功能。
确定好分布后,第二步就是计算出对应分布的三个百分位数:0.5分位数、0.99865分位数和0.00135分位数(我们可以通过“概率分布图”计算这三个百分位数)。
把计算出来的三个百分位数带入“ISO方法”的公式得到Pp和Ppk。
收起阅读 »
非正态解决方案
如果您使用为正态数据设计的能力分析,您的数据必须服从正态分布。
对于上面的这些公式,我相信很多朋友比较熟悉(不同教材在公式写法和叫法上可能稍微不同),但我们今天讨论的不是这组公式,为什么呢?因为上面这些公式只适用于正态数据,而我们今天想分享的是非正态数据的能力分析。
对于非正态数据,我们可以通过以下方法来获得准确描述生成非正态数据的过程的能力指数。
正如你所看到的,解决方法有很多,当然方法选择不同结果肯定是有差异的,那么问题又来了,哪个方法是比较合适的呢?别急,我们可以先参考以下路径图帮助我们选择。
在上一篇文章中我们分享了变换的方法(Box-Cox变换),在这篇文章中,我们打算找到拟合数据的合适分布(除了正态分布外,Minitab在这里还提供了其他13种分布),采用非正态的方法来计算Ppk(注意,由于是非正态分布,这时候就无法计算Cp/CpK了)。
拟合其他分布法(ISO方法)原理
对于非正态数据,Minitab后台提供两种算法(21版本中,默认算法为“Z值法”)
但是,我们今天要分享的是“ISO方法”,原因很简单,这种算法大家在六西格玛相关课程和教材中其实学过了(先混个脸熟)。
介绍“ISO方法”之前,我们首先来回顾一下能力分析的含义(如下图所示)。
其中,“客户之声”就是客户给定的公差带宽(USL-LSL),关键是怎么得到“过程之声”。
回想一下,如果数据服从正态分布,我们是怎么估计“过程之声”的?用正态分布的均值做为中心位置,用平均值±3标准差来构造一个99.73%的区间来做为“过程之声”的估计。
那如果是非正态数据呢,我们是不是也可以想办法来获得“过程之声”?但是很多非正态数据的分布不像正态分布那样是对称的(如下面的Weibull分布)。
那么这时候怎么获得中心位置和99.73%的区间呢?我们可以借助“ISO算法”通过计算分位数方法来估计“过程之声”。
说明:
表示指定分布的第0.99865个百分位数(太专业了,看不懂?直白一点说,分布选择不同,计算出来的结果不一样,所以我们需要找到合适的分布)。说到这里我相信大家应该理解了为什么在用Minitab做非正态数据能力分析时需要我们先指定分布了。
拟合其他分布法(ISO方法)计算
基于以上分析,我们可以通过以下三步骤来计算非正态数据的过程能力。
找到合适的分布(除正态分布外有13种选择),怎么确定哪种分布拟合的比较好呢?我们可以利用Minitab中的“个体分布标识”功能。
确定好分布后,第二步就是计算出对应分布的三个百分位数:0.5分位数、0.99865分位数和0.00135分位数(我们可以通过“概率分布图”计算这三个百分位数)。
把计算出来的三个百分位数带入“ISO方法”的公式得到Pp和Ppk。
收起阅读 »
方差分析在等离子蚀刻中的应用
一、案例背景
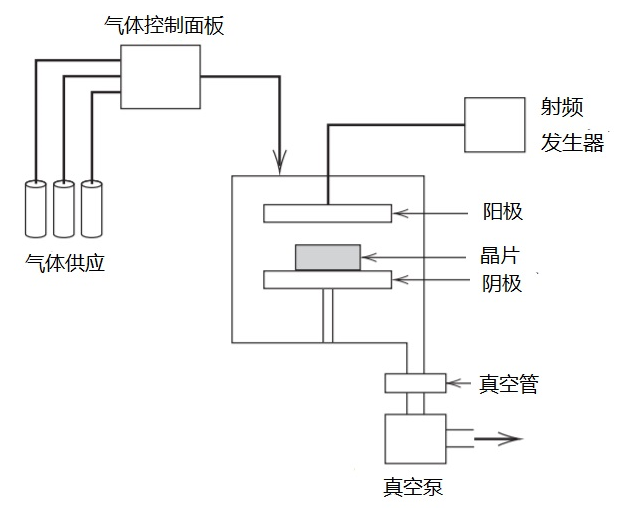
在集成电路的许多生产步骤中,晶片被一层材料(如二氧化硅或某种金属)完全覆盖。通过对掩模的蚀刻有选择性地除去不需要的材料,从而创建电路模板、电互连以及必须扩散的或者金属沉积的区域。等离子蚀刻工序在这个操作中被广泛使用,特别是在几何对象比较小的情况下的应用。下图展示了一种典型的单晶片蚀刻设备的重要特征。特此说明:案例来自蒙哥马利的《实验设计与分析》一书。
射频(RF)发生器提供能源使得电极之间的间隙产生等离子,等离子体的化学种类是由所使用的特定气体决定的。碳氟化合物,比如CF4(四氟甲烷)或C2F6(六氟乙烷),通常被用在等离子蚀刻上。但是根据应用情况的不同,也常使用其他的气体或混合气体。
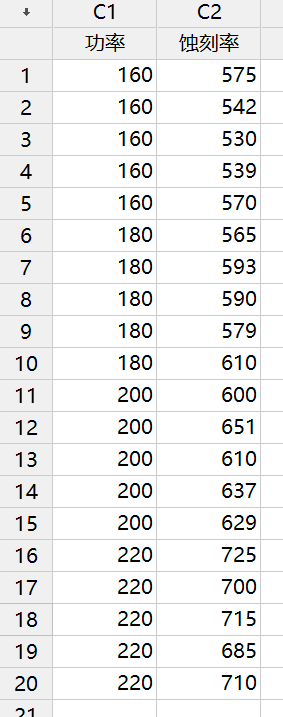
工程师要研究这套设备的RF功率设置与蚀刻率间的关系。实验目的是开发工程师要确定RF功率设置是否影响蚀刻率。她选定了气体(C2F6)和间隙(0.80 cm),想检验RF功率的4个水平:160W,180W,200W和220W。她决定在RF功率的每个水平上检验5个晶片。
这是一个因子水平为4和重复次数为5的单因子实验。这20个试验都是按照随机顺序进行的。
二、分析之前注意事项
一个好的试验设计分析,重点和难点往往不是在如何“分析”它(我相信通过本次案例,您也会借助Minitab做方差分析),而是在于如何“设计”这个试验,如何制定数据收集计划。对于设计得很差的试验,你做不了任何分析。你只能搬出具尸体,找出他的死亡原因。
Fisher曾经说过设计一个试验就像和魔鬼玩机会游戏一样,你无法预测他会使出什么样的高招让你的努力作废。在单晶片蚀刻中亦是如此,为防止未知讨厌变量的影响,随机化试验顺序是必要的,因为实验中讨厌变量的变化也许会超出控制范围。从而损害实验结果。为了方便大家对随机化的理解,请参考如下说明图。
知道了随机化的重要性,哪如何做到随机化呢?我发现很多朋友喜欢按照顺序做试验(先把功率为160的五次试验做完,再做180的,再做200的,最后再做功率为220的五次试验),这就不是我们所说的随机化顺序了。这种按照顺序方式做试验,最后的统计结论往往会变成管理者会议上的争论(我会在后续文章中分享这个故事)。
为了随机化,我们可以在Minitab中执行以下操作:
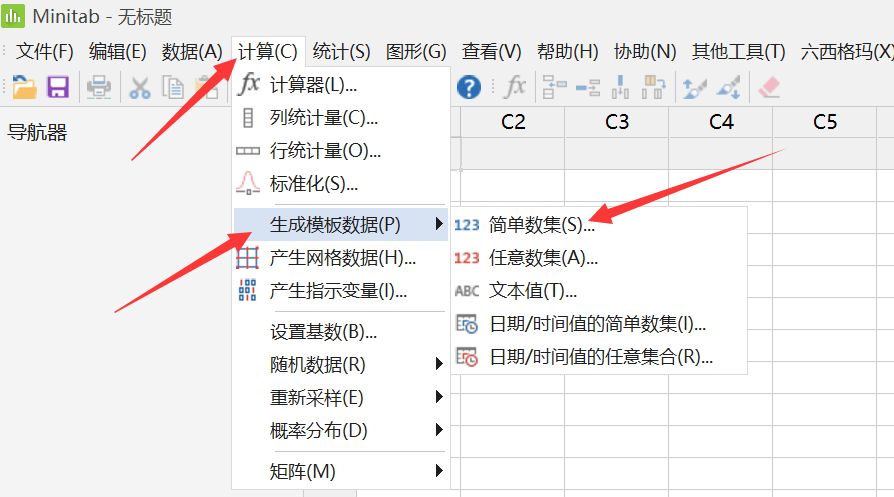
1.首先我们新建一“标准顺序”列,编号从1到20。
计算-生成模板数据-简单数集
2.计算-生成模板数据-任意数集
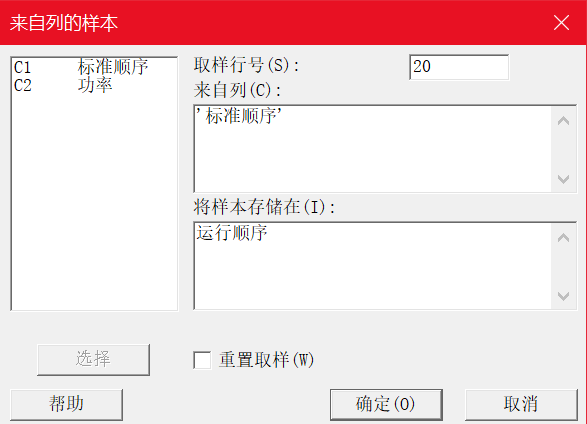
3.计算-随机数据-来自列的样本
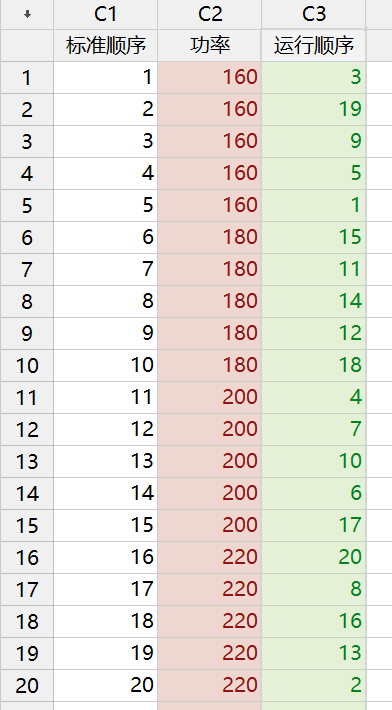
我们按照生成的随机化顺序(C3列运行序)做试验,第一次做功率为160的,第二次做功率为220的……(试验都做了,钱都花了,就不要想着偷懒了)。
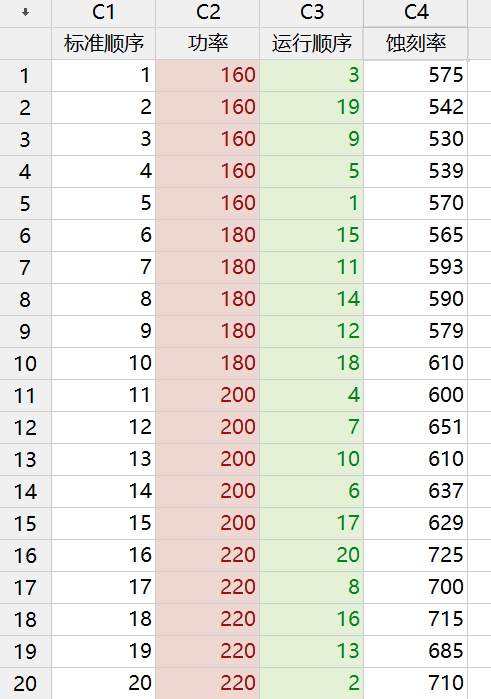
最终,得到以上试验数据(按照随机化顺序做的)。
三、Minitab操作步骤
在这里我们是想对单因子(功率)4个水平(160、180、200、220)下的蚀刻率均值做比较,这里我们可以使用方差分析。
1.路径:统计-方差分析-单因子
2.Minitab结果解释
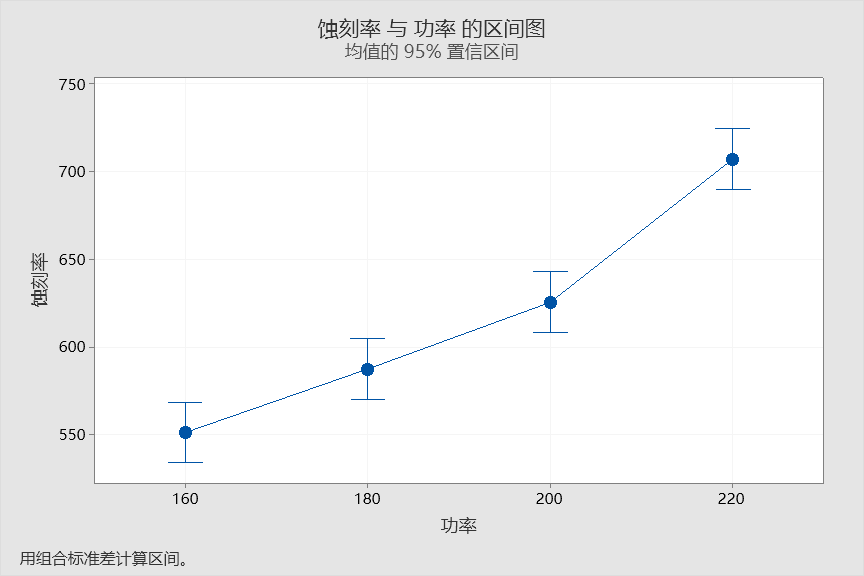
从“方差分析”表中,我们看到检验的P值等于0,小于0.05,故拒绝所有均值都相等的原假设,从而得到4个功率下蚀刻率均值有显著差异的结论。Minitab还同步输出了下面的区间图,从图中可以发现随着功率增大蚀刻率增大。
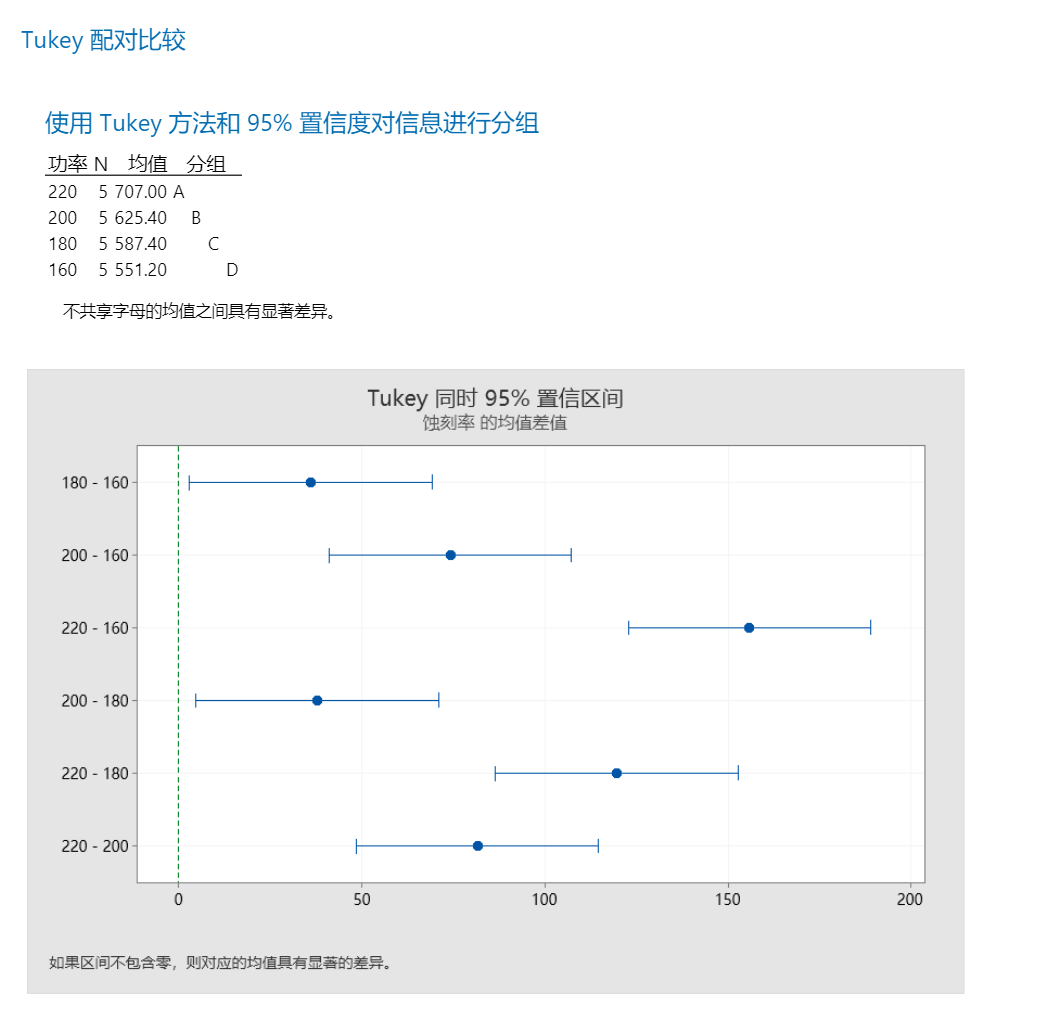
当然,你也可以进一步做多重比较。
四、小结
本篇文章着重向大家强调了试验中“随机化”的重要性以及如何安排随机化试验,我也希望大家能够在后续试验安排做到随机化(我知道,这确实不容易)。一个研究所需要的准备工作远比选择一个统计设计重要得多,统计基于你试验收集的数据,它不会撒谎。但如果试验本身就安排不合理(如没有随机化),利用这个试验获得的数据执行统计分析,那么这时候得到的统计结论有多少能够反映实际生产状况就不得而知了。 收起阅读 »
在集成电路的许多生产步骤中,晶片被一层材料(如二氧化硅或某种金属)完全覆盖。通过对掩模的蚀刻有选择性地除去不需要的材料,从而创建电路模板、电互连以及必须扩散的或者金属沉积的区域。等离子蚀刻工序在这个操作中被广泛使用,特别是在几何对象比较小的情况下的应用。下图展示了一种典型的单晶片蚀刻设备的重要特征。特此说明:案例来自蒙哥马利的《实验设计与分析》一书。
射频(RF)发生器提供能源使得电极之间的间隙产生等离子,等离子体的化学种类是由所使用的特定气体决定的。碳氟化合物,比如CF4(四氟甲烷)或C2F6(六氟乙烷),通常被用在等离子蚀刻上。但是根据应用情况的不同,也常使用其他的气体或混合气体。
工程师要研究这套设备的RF功率设置与蚀刻率间的关系。实验目的是开发工程师要确定RF功率设置是否影响蚀刻率。她选定了气体(C2F6)和间隙(0.80 cm),想检验RF功率的4个水平:160W,180W,200W和220W。她决定在RF功率的每个水平上检验5个晶片。
这是一个因子水平为4和重复次数为5的单因子实验。这20个试验都是按照随机顺序进行的。
二、分析之前注意事项
一个好的试验设计分析,重点和难点往往不是在如何“分析”它(我相信通过本次案例,您也会借助Minitab做方差分析),而是在于如何“设计”这个试验,如何制定数据收集计划。对于设计得很差的试验,你做不了任何分析。你只能搬出具尸体,找出他的死亡原因。
Fisher曾经说过设计一个试验就像和魔鬼玩机会游戏一样,你无法预测他会使出什么样的高招让你的努力作废。在单晶片蚀刻中亦是如此,为防止未知讨厌变量的影响,随机化试验顺序是必要的,因为实验中讨厌变量的变化也许会超出控制范围。从而损害实验结果。为了方便大家对随机化的理解,请参考如下说明图。
知道了随机化的重要性,哪如何做到随机化呢?我发现很多朋友喜欢按照顺序做试验(先把功率为160的五次试验做完,再做180的,再做200的,最后再做功率为220的五次试验),这就不是我们所说的随机化顺序了。这种按照顺序方式做试验,最后的统计结论往往会变成管理者会议上的争论(我会在后续文章中分享这个故事)。
为了随机化,我们可以在Minitab中执行以下操作:
1.首先我们新建一“标准顺序”列,编号从1到20。
计算-生成模板数据-简单数集
2.计算-生成模板数据-任意数集
3.计算-随机数据-来自列的样本
我们按照生成的随机化顺序(C3列运行序)做试验,第一次做功率为160的,第二次做功率为220的……(试验都做了,钱都花了,就不要想着偷懒了)。
最终,得到以上试验数据(按照随机化顺序做的)。
三、Minitab操作步骤
在这里我们是想对单因子(功率)4个水平(160、180、200、220)下的蚀刻率均值做比较,这里我们可以使用方差分析。
1.路径:统计-方差分析-单因子
2.Minitab结果解释
从“方差分析”表中,我们看到检验的P值等于0,小于0.05,故拒绝所有均值都相等的原假设,从而得到4个功率下蚀刻率均值有显著差异的结论。Minitab还同步输出了下面的区间图,从图中可以发现随着功率增大蚀刻率增大。
当然,你也可以进一步做多重比较。
四、小结
本篇文章着重向大家强调了试验中“随机化”的重要性以及如何安排随机化试验,我也希望大家能够在后续试验安排做到随机化(我知道,这确实不容易)。一个研究所需要的准备工作远比选择一个统计设计重要得多,统计基于你试验收集的数据,它不会撒谎。但如果试验本身就安排不合理(如没有随机化),利用这个试验获得的数据执行统计分析,那么这时候得到的统计结论有多少能够反映实际生产状况就不得而知了。 收起阅读 »
测量系统一致性分析 | 这个汤真的那么辣吗?
熊妈妈已经忍无可忍了。最近一次关于她做的汤有多辣的争论以张牙舞爪而结束,而且把小女孩吓坏了。
熊妈妈认为问题出在小女孩身上。自从有了金凤花姑娘之后,所有人都无法就任何事情达成一致。床不是太软就是太硬。粥不是太烫就是太凉。今晚,金凤花姑娘抱怨汤太辣,熊爸爸抱怨汤不够辣。
为了使家庭恢复安宁,熊妈妈觉得小女孩需要离开。但是,每当熊妈妈提到这点时,熊爸爸就会跑过去为金凤花姑娘辩护。熊妈妈需要使用数据来为自己辩护,她明白该怎么做:使用一种名为“属性一致性分析”的测量系统分析。熊妈妈知道,使用 Minitab中的“协助”会使事情变得简单容易。
首先,她煮了六份汤。在其中的三份汤中,熊妈妈仅添加了足够的胡椒粉和香料,使汤美味但不会太辣。她在其余三份汤中加了过量的辣椒酱。
接着,熊妈妈使用 Minitab来设置、收集和分析数据,她希望确定为什么家庭成员如此频繁地出现意见不一致。
设置属性一致性分析
选择协助 > 测量系统分析 (MSA)…
“协助”显示一个决策树,该决策树中包括用于“评价”数据的 MSA。
熊妈妈打算让每个家庭成员都品尝六份不同的汤,并让他们评价是好(“好喝!”)还是差(“难喝!”)。每个评价者对每份汤都品尝 4 次,因此熊妈妈不仅能够查看不同检验者的意见是否一致,还能查看每个检验者每次品尝后的评价是否一致。
但是,她的数据收集计划能够满足此分析的需要吗?单击“属性一致性工作表”下面的“更多…”即可显示一列需要检查的要求。例如,“协助”建议评价者对相同数量的好和差项目进行评分,还建议至少有 3 个评价者,熊妈妈的计划中涵盖了这两项要求。
现在,熊妈妈确信她的计划非常恰当。她单击“返回”,然后单击“属性一致性工作表”并按如下所示填写对话框:
在单击“确定”之后,Minitab 将针对每个评价者和每份汤生成一组(共四个)随机试验,并创建一个匹配的数据表。
Minitab 还允许打印一整套随时可用的数据收集表单(每个试验和评价者有一份对应的表单)。
接着,熊妈妈加热这六份汤,并让每个检验者按照 Minitab 所指定的随机顺序对每份汤品尝四次。然后,她只需将结果输入到其数据表的相应列中就可以了:
分析数据
将结果输入到工作表中之后,熊妈妈可以继续进行分析。返回到协助 > 测量系统分析 (MSA)…,但这一次的目标是分析数据,而不是设置研究:
按如上所示填写对话框,单击“确定”。Minitab 将生成所有输出,熊妈妈需要使用这些输出来为自己辩护。
汇总报告显示,总体而言,家庭成员正确识别汤辛辣程度的正确率仅为 75%。按评价者计算的准确度百分比显示每个评价者对汤进行识别的准确度。熊妈妈和熊宝宝的得分最高,他们的准确度分别为 95.8% 和 87.5%。熊爸爸的准确度为 79.2%,不算太低。
但是,金凤花姑娘的准确度为 37.5%,很低。
“协助”的准确度报告为熊妈妈提供了有关每个评价者表现的具体细节。准确度报告右侧的按评价者计算的准确度百分比图和标准图显示,在三头熊中,每头熊都非常擅长识别美味的汤,但是,金凤花姑娘正确识别出美味的汤的概率不到 20%。
“协助”还有另外两个输出——“误分类报告”和“报告卡”。
证据在汤里
通过属性一致性分析的结果,可以清楚地判定有关汤辣不辣的大多数不一致源自何处,以及(按照熊妈妈的观点)不一致应当在何处终结。使用由“协助”创建的简单图形,甚至连熊爸爸也可以轻松看出,金凤花姑娘对汤的评价分歧可能会导致家庭成员产生冲突。
无论您喜欢清淡的汤还是喜欢超辣的汤,您都已经成功完成了此测量系统分析。您已了解如何创建属性一致性分析工作表,以及如何分析您收集的数据以使用“协助”来确定评价者在何处一致,在何处不一致。 收起阅读 »
熊妈妈认为问题出在小女孩身上。自从有了金凤花姑娘之后,所有人都无法就任何事情达成一致。床不是太软就是太硬。粥不是太烫就是太凉。今晚,金凤花姑娘抱怨汤太辣,熊爸爸抱怨汤不够辣。
为了使家庭恢复安宁,熊妈妈觉得小女孩需要离开。但是,每当熊妈妈提到这点时,熊爸爸就会跑过去为金凤花姑娘辩护。熊妈妈需要使用数据来为自己辩护,她明白该怎么做:使用一种名为“属性一致性分析”的测量系统分析。熊妈妈知道,使用 Minitab中的“协助”会使事情变得简单容易。
首先,她煮了六份汤。在其中的三份汤中,熊妈妈仅添加了足够的胡椒粉和香料,使汤美味但不会太辣。她在其余三份汤中加了过量的辣椒酱。
接着,熊妈妈使用 Minitab来设置、收集和分析数据,她希望确定为什么家庭成员如此频繁地出现意见不一致。
设置属性一致性分析
选择协助 > 测量系统分析 (MSA)…
“协助”显示一个决策树,该决策树中包括用于“评价”数据的 MSA。
熊妈妈打算让每个家庭成员都品尝六份不同的汤,并让他们评价是好(“好喝!”)还是差(“难喝!”)。每个评价者对每份汤都品尝 4 次,因此熊妈妈不仅能够查看不同检验者的意见是否一致,还能查看每个检验者每次品尝后的评价是否一致。
但是,她的数据收集计划能够满足此分析的需要吗?单击“属性一致性工作表”下面的“更多…”即可显示一列需要检查的要求。例如,“协助”建议评价者对相同数量的好和差项目进行评分,还建议至少有 3 个评价者,熊妈妈的计划中涵盖了这两项要求。
现在,熊妈妈确信她的计划非常恰当。她单击“返回”,然后单击“属性一致性工作表”并按如下所示填写对话框:
在单击“确定”之后,Minitab 将针对每个评价者和每份汤生成一组(共四个)随机试验,并创建一个匹配的数据表。
Minitab 还允许打印一整套随时可用的数据收集表单(每个试验和评价者有一份对应的表单)。
接着,熊妈妈加热这六份汤,并让每个检验者按照 Minitab 所指定的随机顺序对每份汤品尝四次。然后,她只需将结果输入到其数据表的相应列中就可以了:
分析数据
将结果输入到工作表中之后,熊妈妈可以继续进行分析。返回到协助 > 测量系统分析 (MSA)…,但这一次的目标是分析数据,而不是设置研究:
按如上所示填写对话框,单击“确定”。Minitab 将生成所有输出,熊妈妈需要使用这些输出来为自己辩护。
汇总报告显示,总体而言,家庭成员正确识别汤辛辣程度的正确率仅为 75%。按评价者计算的准确度百分比显示每个评价者对汤进行识别的准确度。熊妈妈和熊宝宝的得分最高,他们的准确度分别为 95.8% 和 87.5%。熊爸爸的准确度为 79.2%,不算太低。
但是,金凤花姑娘的准确度为 37.5%,很低。
“协助”的准确度报告为熊妈妈提供了有关每个评价者表现的具体细节。准确度报告右侧的按评价者计算的准确度百分比图和标准图显示,在三头熊中,每头熊都非常擅长识别美味的汤,但是,金凤花姑娘正确识别出美味的汤的概率不到 20%。
“协助”还有另外两个输出——“误分类报告”和“报告卡”。
证据在汤里
通过属性一致性分析的结果,可以清楚地判定有关汤辣不辣的大多数不一致源自何处,以及(按照熊妈妈的观点)不一致应当在何处终结。使用由“协助”创建的简单图形,甚至连熊爸爸也可以轻松看出,金凤花姑娘对汤的评价分歧可能会导致家庭成员产生冲突。
无论您喜欢清淡的汤还是喜欢超辣的汤,您都已经成功完成了此测量系统分析。您已了解如何创建属性一致性分析工作表,以及如何分析您收集的数据以使用“协助”来确定评价者在何处一致,在何处不一致。 收起阅读 »
测量系统一致性分析 | 这个汤真的那么辣吗?
熊妈妈已经忍无可忍了。最近一次关于她做的汤有多辣的争论以张牙舞爪而结束,而且把小女孩吓坏了。
熊妈妈认为问题出在小女孩身上。自从有了金凤花姑娘之后,所有人都无法就任何事情达成一致。床不是太软就是太硬。粥不是太烫就是太凉。今晚,金凤花姑娘抱怨汤太辣,熊爸爸抱怨汤不够辣。
为了使家庭恢复安宁,熊妈妈觉得小女孩需要离开。但是,每当熊妈妈提到这点时,熊爸爸就会跑过去为金凤花姑娘辩护。熊妈妈需要使用数据来为自己辩护,她明白该怎么做:使用一种名为“属性一致性分析”的测量系统分析。熊妈妈知道,使用 Minitab中的“协助”会使事情变得简单容易。
首先,她煮了六份汤。在其中的三份汤中,熊妈妈仅添加了足够的胡椒粉和香料,使汤美味但不会太辣。她在其余三份汤中加了过量的辣椒酱。
接着,熊妈妈使用 Minitab来设置、收集和分析数据,她希望确定为什么家庭成员如此频繁地出现意见不一致。
设置属性一致性分析
选择协助 > 测量系统分析 (MSA)…
“协助”显示一个决策树,该决策树中包括用于“评价”数据的 MSA。
熊妈妈打算让每个家庭成员都品尝六份不同的汤,并让他们评价是好(“好喝!”)还是差(“难喝!”)。每个评价者对每份汤都品尝 4 次,因此熊妈妈不仅能够查看不同检验者的意见是否一致,还能查看每个检验者每次品尝后的评价是否一致。
但是,她的数据收集计划能够满足此分析的需要吗?单击“属性一致性工作表”下面的“更多…”即可显示一列需要检查的要求。例如,“协助”建议评价者对相同数量的好和差项目进行评分,还建议至少有 3 个评价者,熊妈妈的计划中涵盖了这两项要求。
现在,熊妈妈确信她的计划非常恰当。她单击“返回”,然后单击“属性一致性工作表”并按如下所示填写对话框:
在单击“确定”之后,Minitab 将针对每个评价者和每份汤生成一组(共四个)随机试验,并创建一个匹配的数据表。
Minitab 还允许打印一整套随时可用的数据收集表单(每个试验和评价者有一份对应的表单)。
接着,熊妈妈加热这六份汤,并让每个检验者按照 Minitab 所指定的随机顺序对每份汤品尝四次。然后,她只需将结果输入到其数据表的相应列中就可以了:
分析数据
将结果输入到工作表中之后,熊妈妈可以继续进行分析。返回到协助 > 测量系统分析 (MSA)…,但这一次的目标是分析数据,而不是设置研究:
按如上所示填写对话框,单击“确定”。Minitab 将生成所有输出,熊妈妈需要使用这些输出来为自己辩护。
汇总报告显示,总体而言,家庭成员正确识别汤辛辣程度的正确率仅为 75%。按评价者计算的准确度百分比显示每个评价者对汤进行识别的准确度。熊妈妈和熊宝宝的得分最高,他们的准确度分别为 95.8% 和 87.5%。熊爸爸的准确度为 79.2%,不算太低。
但是,金凤花姑娘的准确度为 37.5%,很低。
“协助”的准确度报告为熊妈妈提供了有关每个评价者表现的具体细节。准确度报告右侧的按评价者计算的准确度百分比图和标准图显示,在三头熊中,每头熊都非常擅长识别美味的汤,但是,金凤花姑娘正确识别出美味的汤的概率不到 20%。
“协助”还有另外两个输出——“误分类报告”和“报告卡”。
证据在汤里
通过属性一致性分析的结果,可以清楚地判定有关汤辣不辣的大多数不一致源自何处,以及(按照熊妈妈的观点)不一致应当在何处终结。使用由“协助”创建的简单图形,甚至连熊爸爸也可以轻松看出,金凤花姑娘对汤的评价分歧可能会导致家庭成员产生冲突。
无论您喜欢清淡的汤还是喜欢超辣的汤,您都已经成功完成了此测量系统分析。您已了解如何创建属性一致性分析工作表,以及如何分析您收集的数据以使用“协助”来确定评价者在何处一致,在何处不一致。 收起阅读 »
熊妈妈认为问题出在小女孩身上。自从有了金凤花姑娘之后,所有人都无法就任何事情达成一致。床不是太软就是太硬。粥不是太烫就是太凉。今晚,金凤花姑娘抱怨汤太辣,熊爸爸抱怨汤不够辣。
为了使家庭恢复安宁,熊妈妈觉得小女孩需要离开。但是,每当熊妈妈提到这点时,熊爸爸就会跑过去为金凤花姑娘辩护。熊妈妈需要使用数据来为自己辩护,她明白该怎么做:使用一种名为“属性一致性分析”的测量系统分析。熊妈妈知道,使用 Minitab中的“协助”会使事情变得简单容易。
首先,她煮了六份汤。在其中的三份汤中,熊妈妈仅添加了足够的胡椒粉和香料,使汤美味但不会太辣。她在其余三份汤中加了过量的辣椒酱。
接着,熊妈妈使用 Minitab来设置、收集和分析数据,她希望确定为什么家庭成员如此频繁地出现意见不一致。
设置属性一致性分析
选择协助 > 测量系统分析 (MSA)…
“协助”显示一个决策树,该决策树中包括用于“评价”数据的 MSA。
熊妈妈打算让每个家庭成员都品尝六份不同的汤,并让他们评价是好(“好喝!”)还是差(“难喝!”)。每个评价者对每份汤都品尝 4 次,因此熊妈妈不仅能够查看不同检验者的意见是否一致,还能查看每个检验者每次品尝后的评价是否一致。
但是,她的数据收集计划能够满足此分析的需要吗?单击“属性一致性工作表”下面的“更多…”即可显示一列需要检查的要求。例如,“协助”建议评价者对相同数量的好和差项目进行评分,还建议至少有 3 个评价者,熊妈妈的计划中涵盖了这两项要求。
现在,熊妈妈确信她的计划非常恰当。她单击“返回”,然后单击“属性一致性工作表”并按如下所示填写对话框:
在单击“确定”之后,Minitab 将针对每个评价者和每份汤生成一组(共四个)随机试验,并创建一个匹配的数据表。
Minitab 还允许打印一整套随时可用的数据收集表单(每个试验和评价者有一份对应的表单)。
接着,熊妈妈加热这六份汤,并让每个检验者按照 Minitab 所指定的随机顺序对每份汤品尝四次。然后,她只需将结果输入到其数据表的相应列中就可以了:
分析数据
将结果输入到工作表中之后,熊妈妈可以继续进行分析。返回到协助 > 测量系统分析 (MSA)…,但这一次的目标是分析数据,而不是设置研究:
按如上所示填写对话框,单击“确定”。Minitab 将生成所有输出,熊妈妈需要使用这些输出来为自己辩护。
汇总报告显示,总体而言,家庭成员正确识别汤辛辣程度的正确率仅为 75%。按评价者计算的准确度百分比显示每个评价者对汤进行识别的准确度。熊妈妈和熊宝宝的得分最高,他们的准确度分别为 95.8% 和 87.5%。熊爸爸的准确度为 79.2%,不算太低。
但是,金凤花姑娘的准确度为 37.5%,很低。
“协助”的准确度报告为熊妈妈提供了有关每个评价者表现的具体细节。准确度报告右侧的按评价者计算的准确度百分比图和标准图显示,在三头熊中,每头熊都非常擅长识别美味的汤,但是,金凤花姑娘正确识别出美味的汤的概率不到 20%。
“协助”还有另外两个输出——“误分类报告”和“报告卡”。
证据在汤里
通过属性一致性分析的结果,可以清楚地判定有关汤辣不辣的大多数不一致源自何处,以及(按照熊妈妈的观点)不一致应当在何处终结。使用由“协助”创建的简单图形,甚至连熊爸爸也可以轻松看出,金凤花姑娘对汤的评价分歧可能会导致家庭成员产生冲突。
无论您喜欢清淡的汤还是喜欢超辣的汤,您都已经成功完成了此测量系统分析。您已了解如何创建属性一致性分析工作表,以及如何分析您收集的数据以使用“协助”来确定评价者在何处一致,在何处不一致。 收起阅读 »
二值响应DOE-汽车挡风玻璃断裂问题
二值响应DOE
传统实验设计的因子类型可以是连续型的也可以是文本型的,而响应变量都是连续型的,如我们想考察材料类型、注塑压力、注塑温度、冷却温度对绝缘强度的影响。现在Minitab 21中新增了二值响应DOE的功能,所谓二值响应就是结果只有两种可能,是/否,好/坏,合格/不合格。二值响应DOE,您可以在Minitab 21的以下分析中找到。
筛选设计
因子设计
响应曲面设计
问题背景
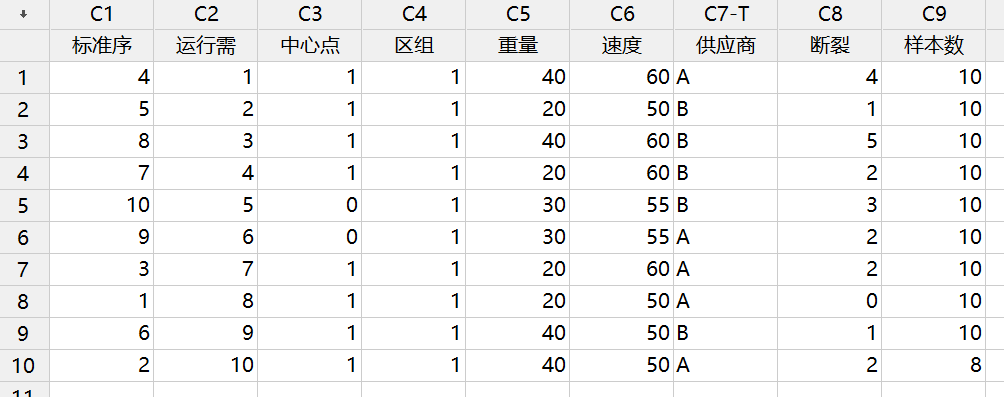
一家汽车制造商想观察由于外来物质损害挡风玻璃所产生的裂纹,他们考虑了三个因子:外来粒子的速度、粒子重量和玻璃供应商。
A: 颗粒的速度(mph),低水平:50, 高水平:60
B: 颗粒的重量(gram),低水平:20, 高水平:40
C: 挡风玻璃的供应商:低水平:A,高水平:B
数据收集
在一个特殊的设计实验房间里,一种颗粒被射向固定于20英尺远的挡风玻璃,一个检验员记录挡风玻璃是否产生裂纹,每种挡风玻璃只使用一次。制造商具有进行对100种挡风玻璃进行实验的资金、时间和材料,允许研究者试验10种挡风玻璃的样本大小。每8个因子的组合和两个中心点。然而,从供应商A只能获得48种挡风玻璃,因此,最后一轮实验只包括8种挡风玻璃样本。
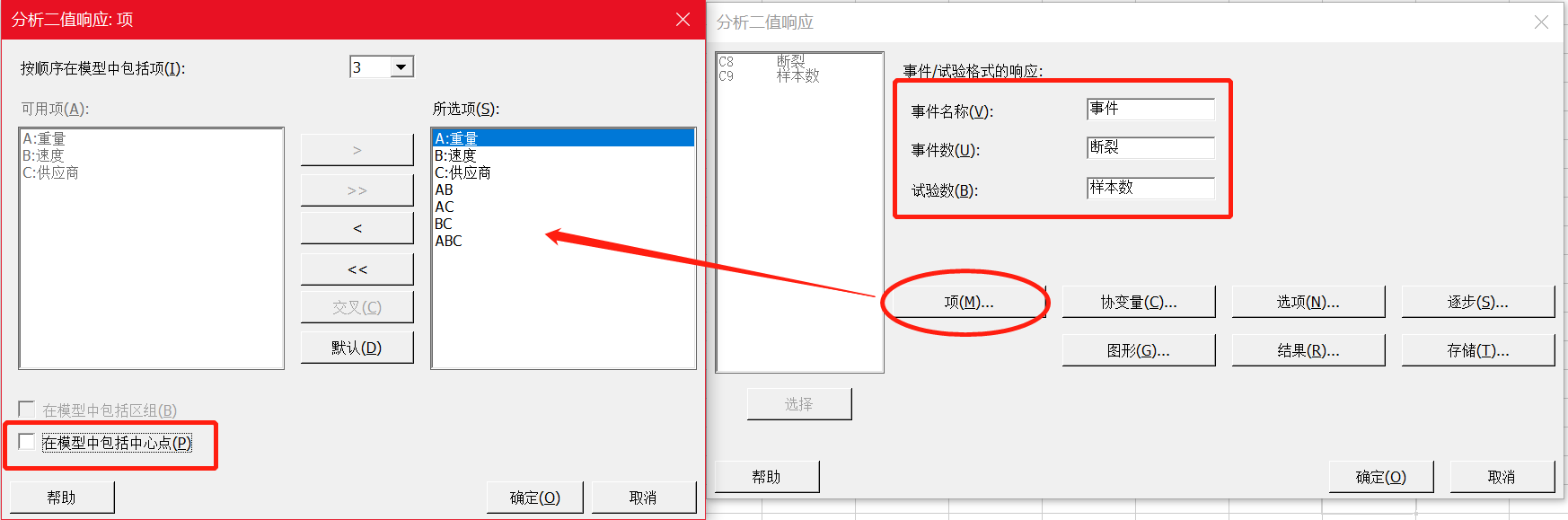
分析二值DOE
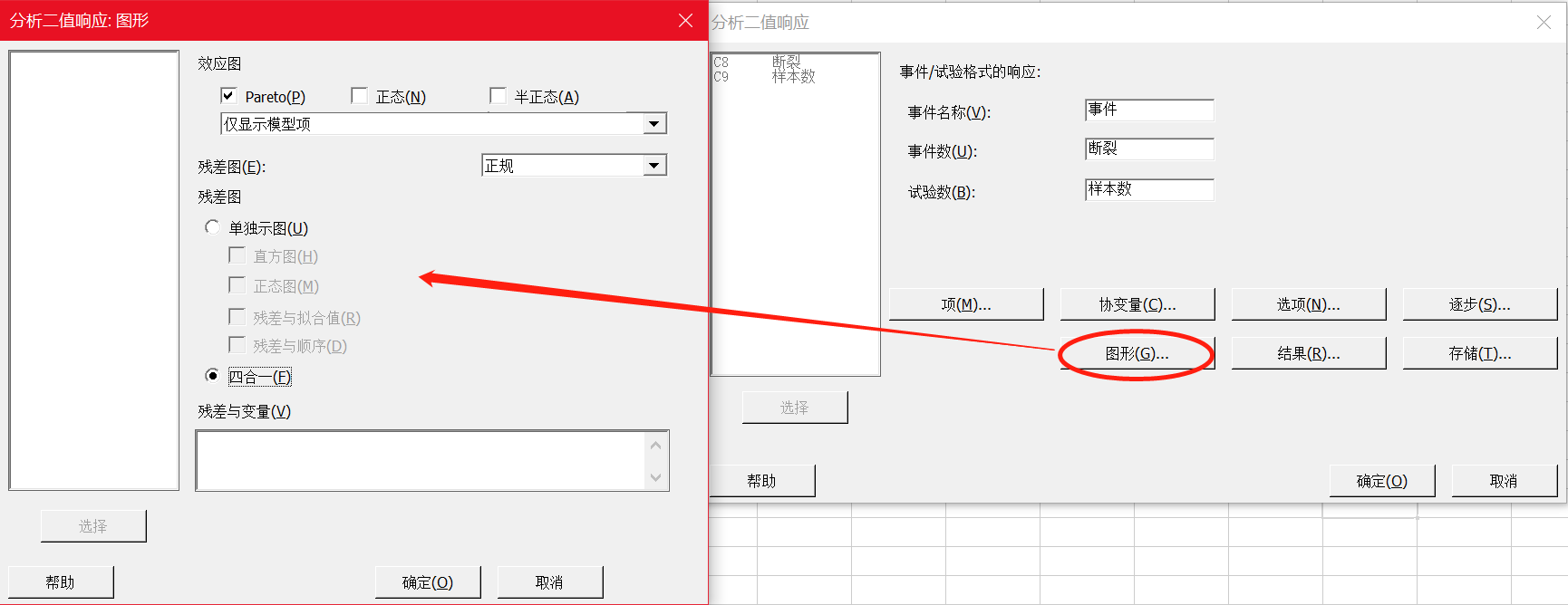
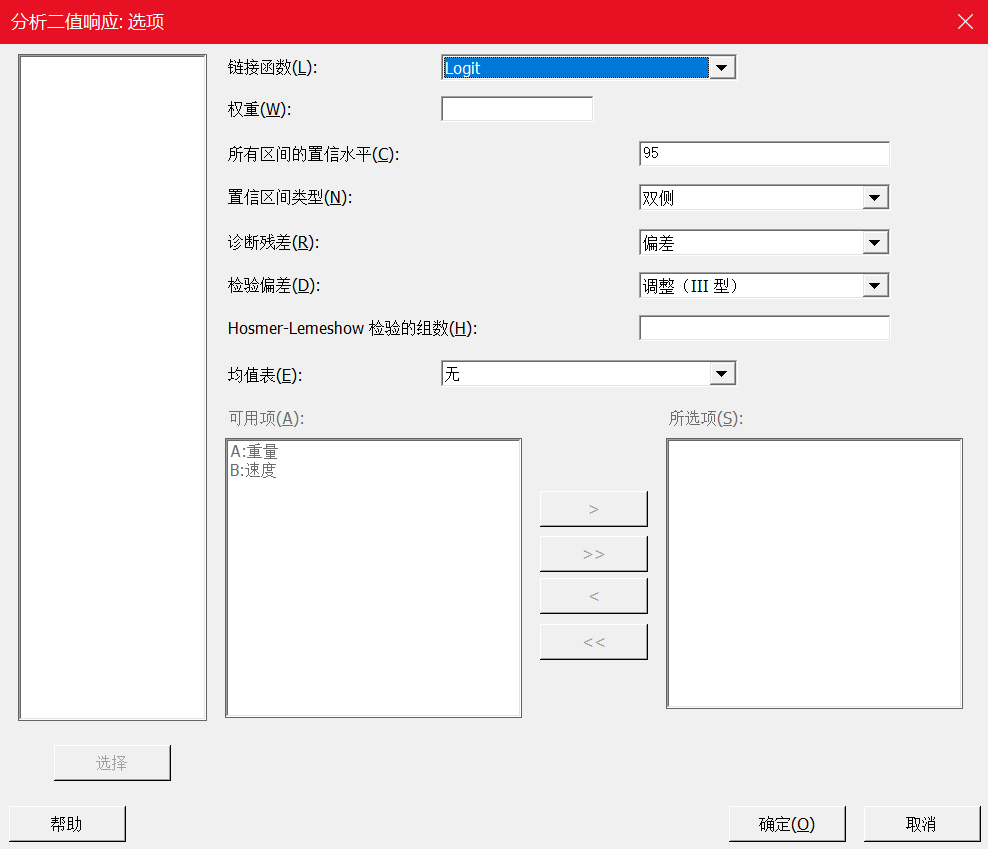
在Minitab 21的二值响应DOE分析种,除了主对话框跟经典实验设计有比较大区别以外,其他选项,比如“项”、“图形”中的设置是没有差别的。
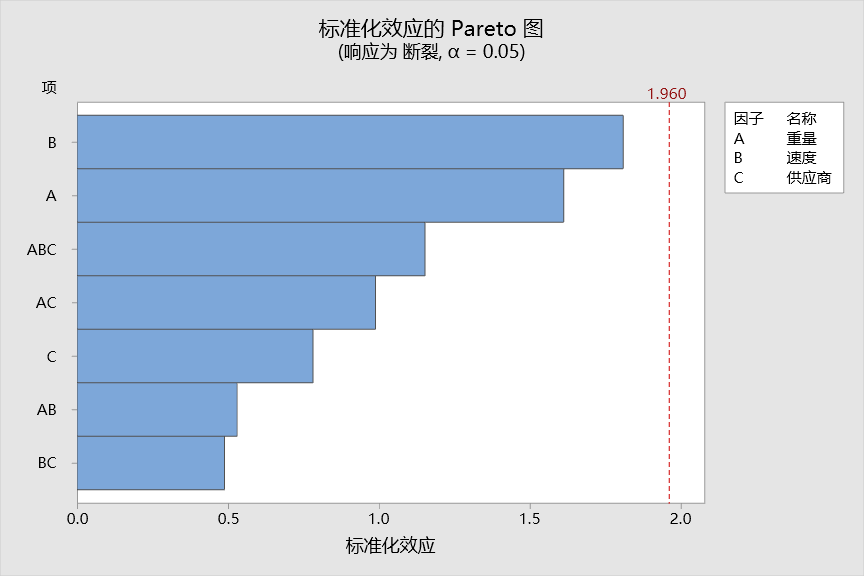
在“项”中,我们第一次拟合模型时,把所有的项都考虑进来(在下面分析中有一个陷阱,请注意哦)。
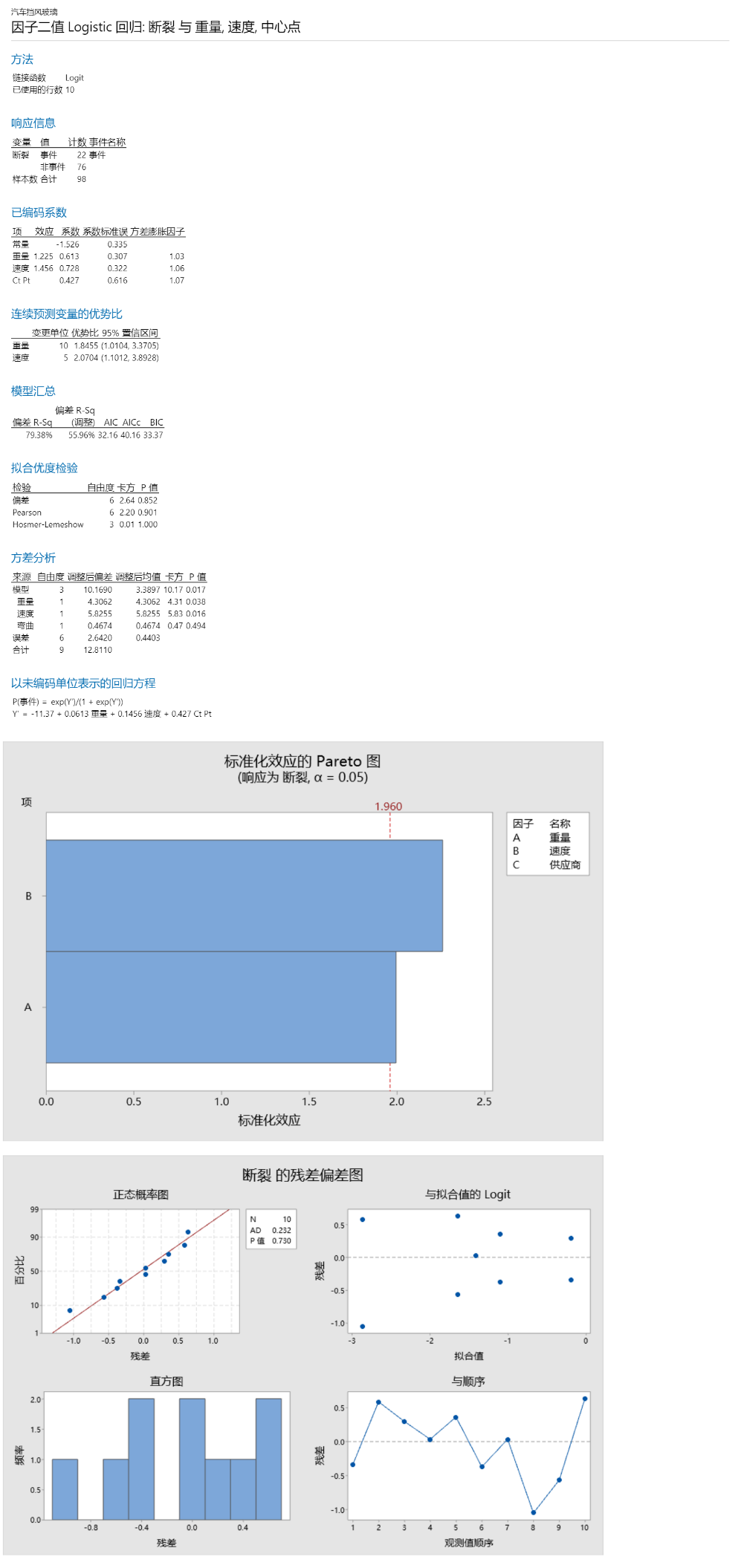
所有对话框点击确定后,得到如下结果。
注意:当我们把所有项都加入到模型中,这时候我们可以看到没有显著的项,此时不要急着下结论。这时候一般的做法是先删除高阶交互作用项。
删除三阶交互作用项和所有二阶交互作用项以后,我们可以看到这时候A和B变成显著的了,C仍然不显著,在下一步优化中需要删除掉。我们得到以下的最终结果。
优势比
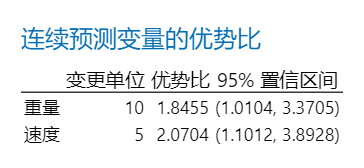
仅当您为具有二元响应的模型选择 logit 链接函数时才提供优势比。在这种情况下,优势比可用于解释预测变量与响应之间的关系。
连续预测变量的优势比:优势比大于 1 表示在预测变量越大,事件发生的几率越大。优势比小于 1 表示预测变量越大,事件发生的几率越小。在当前结果中,该模型使用颗粒的重量水平来预测汽车挡风玻璃是否断裂。在此示例中,挡风玻璃断裂为“事件”。每颗粒的重量为10gram,因此研究人员使用10gram作为一个单位变化。优势比约为1.8455。颗粒重量每增加一个单位,挡风玻璃断裂的比率就增加约1.8455倍。颗粒速度的优势比解释结果一样,不再赘述。
类别预测变量(当前结果没有)的优势比:对于类别预测变量,优势比可以比较事件在两个不同的预测变量水平发生的几率。Minitab 通过在水平 A 和水平 B 这两列中列出水平来设置比较。水平 B 是因子的参考水平。优势比大于 1 表示事件在水平 A 下发生的几率大。优势比小于 1 表示事件在水平 A 下发生的几率小。
结论
在Minitab 21中有了二值响应DOE分析,扩展了DOE的功能。当然,在实验设计中我们除了遇到二值响应DOE外,可能还会遇到残差分析有问题需要对响应变量做变换的DOE分析、带区组的实验设计分析等比较复杂的DOE问题。我们将在后续为大家一一分享,如果您还没有使用过Minitab 21,可以登陆Minitab官网下载30天免费试用版哦! 收起阅读 »
传统实验设计的因子类型可以是连续型的也可以是文本型的,而响应变量都是连续型的,如我们想考察材料类型、注塑压力、注塑温度、冷却温度对绝缘强度的影响。现在Minitab 21中新增了二值响应DOE的功能,所谓二值响应就是结果只有两种可能,是/否,好/坏,合格/不合格。二值响应DOE,您可以在Minitab 21的以下分析中找到。
筛选设计
因子设计
响应曲面设计
问题背景
一家汽车制造商想观察由于外来物质损害挡风玻璃所产生的裂纹,他们考虑了三个因子:外来粒子的速度、粒子重量和玻璃供应商。
A: 颗粒的速度(mph),低水平:50, 高水平:60
B: 颗粒的重量(gram),低水平:20, 高水平:40
C: 挡风玻璃的供应商:低水平:A,高水平:B
数据收集
在一个特殊的设计实验房间里,一种颗粒被射向固定于20英尺远的挡风玻璃,一个检验员记录挡风玻璃是否产生裂纹,每种挡风玻璃只使用一次。制造商具有进行对100种挡风玻璃进行实验的资金、时间和材料,允许研究者试验10种挡风玻璃的样本大小。每8个因子的组合和两个中心点。然而,从供应商A只能获得48种挡风玻璃,因此,最后一轮实验只包括8种挡风玻璃样本。
分析二值DOE
在Minitab 21的二值响应DOE分析种,除了主对话框跟经典实验设计有比较大区别以外,其他选项,比如“项”、“图形”中的设置是没有差别的。
在“项”中,我们第一次拟合模型时,把所有的项都考虑进来(在下面分析中有一个陷阱,请注意哦)。
所有对话框点击确定后,得到如下结果。
注意:当我们把所有项都加入到模型中,这时候我们可以看到没有显著的项,此时不要急着下结论。这时候一般的做法是先删除高阶交互作用项。
删除三阶交互作用项和所有二阶交互作用项以后,我们可以看到这时候A和B变成显著的了,C仍然不显著,在下一步优化中需要删除掉。我们得到以下的最终结果。
优势比
仅当您为具有二元响应的模型选择 logit 链接函数时才提供优势比。在这种情况下,优势比可用于解释预测变量与响应之间的关系。
连续预测变量的优势比:优势比大于 1 表示在预测变量越大,事件发生的几率越大。优势比小于 1 表示预测变量越大,事件发生的几率越小。在当前结果中,该模型使用颗粒的重量水平来预测汽车挡风玻璃是否断裂。在此示例中,挡风玻璃断裂为“事件”。每颗粒的重量为10gram,因此研究人员使用10gram作为一个单位变化。优势比约为1.8455。颗粒重量每增加一个单位,挡风玻璃断裂的比率就增加约1.8455倍。颗粒速度的优势比解释结果一样,不再赘述。
类别预测变量(当前结果没有)的优势比:对于类别预测变量,优势比可以比较事件在两个不同的预测变量水平发生的几率。Minitab 通过在水平 A 和水平 B 这两列中列出水平来设置比较。水平 B 是因子的参考水平。优势比大于 1 表示事件在水平 A 下发生的几率大。优势比小于 1 表示事件在水平 A 下发生的几率小。
结论
在Minitab 21中有了二值响应DOE分析,扩展了DOE的功能。当然,在实验设计中我们除了遇到二值响应DOE外,可能还会遇到残差分析有问题需要对响应变量做变换的DOE分析、带区组的实验设计分析等比较复杂的DOE问题。我们将在后续为大家一一分享,如果您还没有使用过Minitab 21,可以登陆Minitab官网下载30天免费试用版哦! 收起阅读 »
优思学院|神奇的统计:从诸葛亮草船借箭说起 - 六西格玛
在抽象的意义下,一切科学都是数学;在理性的世界里,所有的判断都是统计学。─C. R. 劳
从城邦政情到统计学
统计学是透过搜集、整理、分析、描述资料等手段,以推断所测量物的性质、本质乃至未来的一门学科,需要运用许多数学知识。统计起源于何时何地已经很难说清,有人说是古埃及,有人说是古巴比伦,也有史料记载是西元前二千年左右的夏朝,统治者为了征兵和征税而进行了人口统计。
到了周朝,“司书”一职首次在中国历史上出现,相当于今日的行政院主计总处处长。西方最早关于统计的记载则是《圣经.旧约》,引用了犹太人的人口统计结果。
人口统计若仅仅是小范围的,即使包括了人数、年龄、收入、性别、身高、体重等多项指标,也派不上大用场。随着统计人数的增加,例如一座城市的市民、一整个省的女性,以及统计指标的增加,例如健康状况、家庭经济状况和寿命等,才能逐渐体现出统计的规律和价值。
西元前四世纪,亚里斯多德撰写的“城邦政情”(matters of state)共包含了一百五十余种纪要,内容涉及希腊各个城邦的历史、行政、科学、艺术、人口、资源和财富等社会和经济情况及其比较分析。
“城邦政情”式的统计延续了二千多年,直至十七世纪中叶才逐渐被“政治算术”(political arithmetic)这个颇有意味的名称替代,并且很快演化为“统计学”(statistics)。最初,它只是一个德文词汇 statistik,保留了城邦(state)的词根,本义是研究国家和社会状况的数量关系。后来,欧洲各国相继翻译,法文为 statistique,义大利文为 statistica,然后是英文。
值得一提的是,英语中的统计学家和统计员是同一个字,正如数学家和数学工作者是同一个单词一样。日语最初把“统计学”译为“政表”、“政算”、“国势”、“形势”,一八八○年才确定为“统计”。一九○三年,横山雅南的著作《统计讲义录》被译成中文出版,“统计”一词也从日本传到了中国,与“数学”这个词语的来历相同。
既然统计学的主要工作是与资料打交道,资料通常又有随机性,就涉及了另外一个统计学术语─概率。随机意味着不确定性,但也并非没有规律可循,这时就需要用概率来描述。例如,经验告诉我们,投掷硬币出现正面朝上结果的概率约为1/2,投掷骰子结果为六点的概率是1/6。
更多时候,我们需要进行大规模的统计才能知道一件事发生的概率。例如某航班的准点率、某地某日的降水概率。而我们在透过计算获得概率的同时,也掌握了相应的统计规律。不过,统计与概率是有差异的。计算一个有四十位学生的班级是否有人同一天生日的概率,与具体统计他们的生日,两者并不一样,而且不同班级(即便人数相同)的统计结果也不相同。
草船借箭可有其事?
如同脚踏车的发明使得人们扩大了交流范围,弓箭的发明也拓宽了人们的活动范围。有了弓箭,人类便可走出山洞,离开茂密的森林,在广阔的丘陵或平原安家。弓箭不但增强人们的安全防御能力,也帮助他们获取更多猎物,为人类的繁衍创造良好的物质条件。
弓箭大约诞生于三万年前的旧石器时代晚期,它是冷兵器时代最可怕的致命武器。弓箭由弓和箭两部分组成,其中的弓由有弹性的臂和有韧性的弦构成;箭则包括了箭头、箭杆和箭羽,箭头为铜或铁制,杆为竹或木质,羽为鵰或鹰的羽毛。射手拉弓时,手指上还有保护工具。
恩格斯(Friedrich Engels)说过,“弓、弦、箭已经是很复杂的工具,发明这些工具需要长期积累的经验和较为发达的智力。”弓箭的发明或许与音乐的起源有某种关系,二十世纪英国科学史家 J.D.贝尔纳(J. D. Bernal)认为,“弓弦弹出的汪汪粗音可能是弦乐器的起源”。
在《诗经.小雅》里有一首诗写到了“角弓”,即弓箭。这首诗劝告周王不要疏远兄弟亲戚而亲近小人,为民众做出表率。首章四句是:“骍骍角弓,翩其反矣。兄弟昏姻,无胥远矣。”骍骍指的是弦和弓调和的样子,翩是弯曲,昏姻即婚姻或姻亲,意为“把角弓调和绷紧弦,弦松弛的话会转向。兄弟姻亲是一家人,相互亲爱可别疏远”。
中国古代神话有“后羿射日”的故事。古典小说里一方面有许多神箭手,例如吕布辕门射戟、薛仁贵三箭定天下、养由基百步穿杨等,另一方面,打不赢就放箭的例子同样比比皆是,清代如莲居士的传奇小说《说唐》里的罗成武艺高强,最终却陷于淤泥并死于乱箭。
一般士兵的射术可没有神箭手那么精准。假设单次射中目标的概率为 0.1,没射中的概率就是 0.9,连续两次射不中的概率为 0.9×0.9=0.81。依此类推,一百次都射不中的概率为 0.9100≈0.00003,那么至少射中一次的概率为“1–0.00003=99.997%”。
即便要求至少射中目标三次,概率仍高达 98.41%。由此可见,与其费力去找神箭手,不如让一百名士兵乱箭齐发,效果更好。在罗贯中的历史小说《三国演义》里,长坂坡(今湖北荆门)一役成就了赵子龙的传奇,其实曹操下令不许放箭可能也发挥了不可或缺的作用。
再来看诸葛亮草船借箭,传说中取到了十万支箭。依据罗贯中的描述,当时江上大雾弥漫,士兵放箭基本上是闻声寻的,命中概率估计不到 0.1,中间还要调转船身,用另一面接箭,自然会射空。即便射中概率不变,至少也需要射一百万支箭。当时曹操的弓箭手仅一万名,代表每人需射一百支,但专家分析这不太可能,因为古时一个箭壶通常只装二十到三十支箭。
高斯的常态分布曲线
生活中偶有小机率事件发生。例如,据相关统计,飞机失事的机率约为三百万分之一。这个机率听起来很小,但每天都有无数乘客搭乘飞机,全世界的航班累计数量其实颇为惊人,因此偶尔还是会听到飞机失事的消息。
再看另一个例子,二○一○年南非世界杯足球赛期间,生于英国养于德国的“章鱼帝保罗”成为耀眼的明星。保罗八次预测,全部猜对比赛结果,尤其是西班牙战胜荷兰的那场决赛,更让全世界球迷为之侧目。假如没有人为操纵,保罗猜对一次的机率是 0.5,连续八次猜对的机率是 0.0039。我们只能说,小机率事件又一次发生了。
在统计学中,样本的选取也存在小机率事件。例如,从一个装着红球和蓝球的缸中随机拿出球来,哪怕缸中的球多半是红球,取出的样本仍可能是蓝球占多数,由此导出错误的结论:缸中的球多数是蓝色的。有鉴于此,统计学家想了一个办法来提高由样本推断总体特征的能力。
假设有一个装了非常多球的缸,其中红球、蓝球的比例为P:(1–P),P(P≦1)是某个未知的比例。一次从缸中拿出五个球,这是一个样本。设p是所有样本(每个样本均含五个球)中红球比蓝球多(即至少有三个红球)的样本所占比例(p≦1)。根据机率理论,可得 P 和 p 的关系如下:
P 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
p 0.01 0.06 0.16 0.32 0.50 0.68 0.84 0.94 0.99
这就说明,当缸中红球比例为 0.1 时,在抽取的样本中红球占多数的样本比例是很小的。确切地说,在一百个样本中,可能只有一个样本是如此。
如果只是加减和方幂运算,统计学恐怕成不了一门学科,更无法成为与数学并列的一级学科(机率理论是数学下面的二级学科)。幸好,统计学里还有高斯的常态分布理论。
十九世纪下半叶,英国统计学家高尔顿(Francis Galton)和皮尔逊(Karl Pearson)在研究父母身高与子女身高之间的遗传关系时,发现了朝平均数回归的现象,也就是身高不会两极分化。
高尔顿做了著名的钉板实验,他在一块平整的木板上均匀放置了二十排钉子,下排的每根钉子恰好位于上排两根钉子的中间。然后他让一颗小圆球从最顶层中间处滚下来,小圆球碰到钉子后往左或往右滚落的概率各为 0.5。由于钉子的间距正好略大于小圆球的直径,小圆球会再次撞击钉子并往左右滚落,概率同样为 0.5。
高尔顿观察到,小圆球虽然一路碰撞滚落底部,却不会太偏离中心位置。大多数小圆球都集结在底部中心的位置,愈往两边数量愈少。最后,堆积的小圆球形成了一个钟形曲线,这正是由法裔英籍数学家棣美弗(Abraham de Moivre)于一七三三年提出,后以德国数学家高斯(他首先将其应用于天文学研究)的名字来命名的常态分布曲线:
如果考虑滚落在中间6个钉距之间的小圆球,则其概率为上述函数在区间[–3, 3]上的定积分,大约是 99.73%。莎士比亚的诗文和忌日威廉•莎士比亚(W. Shakespeare)是英国大文豪,也被视为有史以来最伟大的文学家之一。 1985年秋天,有位莎翁研究专家在牛津大如果考虑滚落在中间六个钉距之间的小圆球,则其机率为上述函数在区间[–3, 3]上的定积分,大约是99.73%。
莎士比亚的诗文和忌日
莎士比亚是英国大文豪,被视为有史以来最伟大的文学家之一。一九八五年秋天,某位莎翁研究专家在牛津大学博多利图书馆里发现了一首写在纸片上的九节诗。这张纸片已被收藏近二百年,上面的诗歌会是莎翁写的吗?
两年后,两位统计学家研究了这首诗,并与莎士比亚的写作风格进行比对,结果发现它们惊人的一致性。已知莎翁诗文著作中用词总量为 884,647 个,其中 31,534 个是不同的,它们出现的频率如下:
单词使用的频率 1 2 3 4 5 >100
不同的单词数 14376 4343 2292 1463 1043 846
由此可见,莎翁喜欢用新词,他使用一次就舍弃的词高达 45.6%,仅用两次的词占 13.8%。倘若对莎翁的部分作品做同样的统计,不同的词出现的频率会高一些。这首新发现的诗作共有四百二十九个单词,其中有二百五十八个是不同的,观测值与基于莎翁写作风格的预测值相对接近。与此同时,统计学家也调查了与莎翁同时代的著名诗人詹森(S. Johnson)、马娄(C. Marlowe)和邓恩(J. Donne)的写作风格,发现他们的预测值与这首诗的观测值有着统计学上的显著差异。
自此以后,莎士比亚的另外三部著作《罗密欧与茱丽叶》、《汤玛斯.莫尔爵士》和《爱德华三世》也用同样的方法加以验证。因为《罗密欧与茱丽叶》写的是义大利上流社会,而莎翁出身英国平民,过去三个世纪里,包括狄更斯(Charles Dickens)和马克.吐温(Mark Twain)等人都曾怀疑它不是莎士比亚的作品。
苏联作家萧洛霍夫(Mikhail Sholokhov)的传世之作《静静的顿河》(And Quiet Flows the Don)也曾遭受类似质疑。这部小说让萧洛霍夫获得一九六五年的诺贝尔文学奖。一九七四年,另一位流亡的苏联作家索忍尼辛(Aleksandr Solzhenitsyn,一九七○年诺贝尔奖得主)在巴黎公开提出质疑,主张萧洛霍夫当时才二十多岁,不可能写出如此广度和深度的鸿篇钜著,而且书中的内容和写作技巧也不平均。
这场争论一直持续到萧洛霍夫暮年,有人怀疑他抄袭了已故作家克留科夫(F. Kryukov)的作品。一九八四年,一位挪威奥斯陆大学的统计学家率领了一个小组,将萧洛霍夫无争议的作品、《静静的顿河》和克留科夫的作品分为三组,利用统计方法进行分析。
第一,他们统计不同词汇占总词汇量的比例,三组分别为 65.5%、64.6%、58.9%。第二,选择最常见的二十个俄语单词,统计它们出现的频率,三组分别为 22.8%、23.3%、26.2%。第三,统计出现不止一次的词汇所占比例,三组分别为 80.9%、81.9%、76.9%。
无论哪一类统计结果都显示,克留科夫的作品风格与《静静的顿河》之间存在着显著差异,而萧洛霍夫更像《静静的顿河》的作者。在中国,古典小说《红楼梦》的作者同样存有疑问,有红学家认为后四十回与前八十回在风格上有很大差异,因此怀疑是另一个作者所写。假如也使用统计学方法,或许可以帮助鉴别。
二十世纪印度裔美籍统计学家 C.R.劳(C. R. Rao)说过,“假如世上每件事情均不可预测地随机发生,那我们的生活将无法忍受。反之,假如每件事情都是确定的、完全可以预测的,那我们的生活又将十分无趣。”他还指出,“在终极的分析中,一切知识都是历史;在抽象的意义下,一切科学都是数学;在理性的世界里,所有的判断都是统计学。”
最后再回来说说莎士比亚。莎翁的生日与忌日都是四月二十三日,这一天也是西班牙语世界最伟大的作家、《唐吉诃德》作者塞万提斯(Cervantes)的忌日,他们在一六一六年的同一天去世。中国历史上最负盛名的戏剧家之一汤显祖也在这一年去世。这个机率实在太小了,小到我们无法估测,甚至完全可以忽略不计。
【本文节录自《数学的故事》,时报文化出版,作者蔡天新。】 收起阅读 »
优思学院|品质圈QCC是什么?如何有效实施?
原发表于优思学院知乎号
QCC的由來
QCC(Quality Control Circle / Quality Circle),一般称为品质圈,是一个由员工组成的小团体,通过各种团队式的改善活动,开发员工的无限潜能,共同为企业的改进做出贡献,尊重人性,建立一个开朗的工作团体。
品质圈(QCC)最初是由戴明博士(W. Edwards Deming)在20世纪50年代提出,戴明博士称赞丰田是这种做法的典范。 后来,这一想法于1962年在日本各地开始正式化,并由石川馨(Kaoru Ishikawa)等人扩大发展,石川馨是20世纪著名于品质管理的日本学者,他发明了鱼骨图,所以鱼骨图同时也称为石川图。
后来,日本科学家和工程师联盟(JUSE)在日本协调这一項QCC的运动,到了1978年,JUSE在他们的出版物《Gemba to QC Circles》中声称,日本已经有超过100万个品质圈,涉及约1000万个日本工人。
QCC的执行方式
品质圈(QCC)团队的成员通常来自同一工作领域,他们自愿定期聚会,以发现、调查、分析和解决与工作有关的问题。
根据日本的经验,在各种工作场所里95%的问题都可以通过简单的质量控制方法来解决,比如七种质量控制工具、PDCA方法。七种质量控制工具-优思学院七种质量控制工具包括帕累托图、因果图、層別法、查檢表、直方图、散布图与控制图。这些工具将帮助QCC小组系统地进行头脑风暴,并对问题进行批判性分析。然后,通过逻辑思维和经验,大多数在日常工作出现的问题都能得到解决。六西格玛五步法-优思学院另外,六西格玛[1]的五步法,则是一种以数据驱动的方法,较适用于处理复杂和深层次的问题,一般会由更资深的质量人员才可掌握,受过培训和认证的六西格玛绿带和黑带,都是改善深层次问题的专家,他们可以领导改善项目,让流程取得突破性的进展。
为什么QCC是有用的?
基于QCC实践的方案因各种原因而被引入,很多企业无一例外地发现,由于QCC活动,产品和服务的质量得到了改善。QCC活动揭示了各种缺陷,让团队自己进行改善,从而提高了工作满意度,并有助于对员工工作的自豪感,这进一步提高了的产品质量,提高了对质量的认识,并持续改进。
另一个好处是改善双向沟通,管理层变得更加关注员工提出的问题,同時,员工也意识到了组织运行的日常问题。部门之间的沟通也得到改善。当QCC致力于解决他们自己领域的问题时,他们的系统性方法往往揭示了以前未曾预料到的生产流程中的困难原因。一般来说,QCC计划需要与ISO9000质量标准在管理结构和公司内部培训方面有相同的框架。因此,QCC应该是任何公司的全面质量计划的一部分。
每个人对QCC计划所规定的改进的承诺也有助于建立顾客的信心。尽管有些公司并不打算实现纯粹的财务回报,但大多数公司发现,财务利益还是会大大改进。
如何实施QCC?
拥有最成功的QCC项目的公司在早期阶段花了很多时间,以确保在任何QCC活动开始之前,公司的每个人都能得到适当的信息和咨询。通常情况下,资深的质量人员、受过培训和认证的六西格玛绿带和黑带都可以协助进行QCC的宣导工作。一旦建立起来,一个典型的项目将在公司的所有部门、办公室、服务部门和生产部门都有QCC在运作。经验表明,公司的规模对项目的成功并不重要,但它对支持结构和组织有很大影响。
实施的步骤可以包括:
通过管理层的介绍,让管理层了解QCC的过程。
2. 对QCC的可行性进行分析。
3. 成立一个指导委员会。
4. 挑选协调人和内部指导员(可以是六西格玛绿带和黑带)。
5. 选定潜在的初始开展的流程。
6. 向已确定的地区、部门的一线主管介绍QCC。
7. 协调员和中层管理人员接受关于该过程和他们角色的广泛培训。
8. 有兴趣的主管自愿参加并接受培训。
9. 培训结束后,QCC将对向新培训的主管报告的员工进行介绍。
10. 员工自愿成为一个圈子的成员并接受培训。
11. 一个圈子成立并开始工作。
12. 随着兴趣的扩大,更多的圈子被组建。
13. 圈子以系统的方式解决问题,而不仅仅是讨论问题。
14. 管理层必须确保解决方案一旦被接受就能迅速实施。
15. 圈子不为他们的解决方案直接支付报酬,但管理层必须确保适当和恰当的认可。
为了成功实施QCC,必须考虑以下准则:
参与是自愿的。
2. 管理层是支持的。
3. 需要对员工进行授权。
4. 培训是方案的组成部分。
5. 成员作为一个团队工作。
6. 成员解决问题,而不仅仅是发现问题。
QCC的行为准则
在一個QCC小組裡,要成功開展,我們要确保小組的討論和參與可以順利和流暢地進行,才可發揮最大的效果,小組的領導者要确保和思考:每成員都在思考同一个问题吗?是否有鼓励所有的想法的提出(不论好的和坏的)?是否所有的想法都被记录下来了吗?所有成员是否有平等的机会参与?
一般来说,QCC讨论要有一些行为准则,例如:
可以批评想法,但不能批评個人。
2. 唯一愚蠢的问题是没有被问到的问题。
3. 团队中的每个人都要对团队的进展负责。
4. 对他人的想法持开放态度。 收起阅读 »
QCC的由來
QCC(Quality Control Circle / Quality Circle),一般称为品质圈,是一个由员工组成的小团体,通过各种团队式的改善活动,开发员工的无限潜能,共同为企业的改进做出贡献,尊重人性,建立一个开朗的工作团体。
品质圈(QCC)最初是由戴明博士(W. Edwards Deming)在20世纪50年代提出,戴明博士称赞丰田是这种做法的典范。 后来,这一想法于1962年在日本各地开始正式化,并由石川馨(Kaoru Ishikawa)等人扩大发展,石川馨是20世纪著名于品质管理的日本学者,他发明了鱼骨图,所以鱼骨图同时也称为石川图。
后来,日本科学家和工程师联盟(JUSE)在日本协调这一項QCC的运动,到了1978年,JUSE在他们的出版物《Gemba to QC Circles》中声称,日本已经有超过100万个品质圈,涉及约1000万个日本工人。
QCC的执行方式
品质圈(QCC)团队的成员通常来自同一工作领域,他们自愿定期聚会,以发现、调查、分析和解决与工作有关的问题。
根据日本的经验,在各种工作场所里95%的问题都可以通过简单的质量控制方法来解决,比如七种质量控制工具、PDCA方法。七种质量控制工具-优思学院七种质量控制工具包括帕累托图、因果图、層別法、查檢表、直方图、散布图与控制图。这些工具将帮助QCC小组系统地进行头脑风暴,并对问题进行批判性分析。然后,通过逻辑思维和经验,大多数在日常工作出现的问题都能得到解决。六西格玛五步法-优思学院另外,六西格玛[1]的五步法,则是一种以数据驱动的方法,较适用于处理复杂和深层次的问题,一般会由更资深的质量人员才可掌握,受过培训和认证的六西格玛绿带和黑带,都是改善深层次问题的专家,他们可以领导改善项目,让流程取得突破性的进展。
为什么QCC是有用的?
基于QCC实践的方案因各种原因而被引入,很多企业无一例外地发现,由于QCC活动,产品和服务的质量得到了改善。QCC活动揭示了各种缺陷,让团队自己进行改善,从而提高了工作满意度,并有助于对员工工作的自豪感,这进一步提高了的产品质量,提高了对质量的认识,并持续改进。
另一个好处是改善双向沟通,管理层变得更加关注员工提出的问题,同時,员工也意识到了组织运行的日常问题。部门之间的沟通也得到改善。当QCC致力于解决他们自己领域的问题时,他们的系统性方法往往揭示了以前未曾预料到的生产流程中的困难原因。一般来说,QCC计划需要与ISO9000质量标准在管理结构和公司内部培训方面有相同的框架。因此,QCC应该是任何公司的全面质量计划的一部分。
每个人对QCC计划所规定的改进的承诺也有助于建立顾客的信心。尽管有些公司并不打算实现纯粹的财务回报,但大多数公司发现,财务利益还是会大大改进。
如何实施QCC?
拥有最成功的QCC项目的公司在早期阶段花了很多时间,以确保在任何QCC活动开始之前,公司的每个人都能得到适当的信息和咨询。通常情况下,资深的质量人员、受过培训和认证的六西格玛绿带和黑带都可以协助进行QCC的宣导工作。一旦建立起来,一个典型的项目将在公司的所有部门、办公室、服务部门和生产部门都有QCC在运作。经验表明,公司的规模对项目的成功并不重要,但它对支持结构和组织有很大影响。
实施的步骤可以包括:
通过管理层的介绍,让管理层了解QCC的过程。
2. 对QCC的可行性进行分析。
3. 成立一个指导委员会。
4. 挑选协调人和内部指导员(可以是六西格玛绿带和黑带)。
5. 选定潜在的初始开展的流程。
6. 向已确定的地区、部门的一线主管介绍QCC。
7. 协调员和中层管理人员接受关于该过程和他们角色的广泛培训。
8. 有兴趣的主管自愿参加并接受培训。
9. 培训结束后,QCC将对向新培训的主管报告的员工进行介绍。
10. 员工自愿成为一个圈子的成员并接受培训。
11. 一个圈子成立并开始工作。
12. 随着兴趣的扩大,更多的圈子被组建。
13. 圈子以系统的方式解决问题,而不仅仅是讨论问题。
14. 管理层必须确保解决方案一旦被接受就能迅速实施。
15. 圈子不为他们的解决方案直接支付报酬,但管理层必须确保适当和恰当的认可。
为了成功实施QCC,必须考虑以下准则:
参与是自愿的。
2. 管理层是支持的。
3. 需要对员工进行授权。
4. 培训是方案的组成部分。
5. 成员作为一个团队工作。
6. 成员解决问题,而不仅仅是发现问题。
QCC的行为准则
在一個QCC小組裡,要成功開展,我們要确保小組的討論和參與可以順利和流暢地進行,才可發揮最大的效果,小組的領導者要确保和思考:每成員都在思考同一个问题吗?是否有鼓励所有的想法的提出(不论好的和坏的)?是否所有的想法都被记录下来了吗?所有成员是否有平等的机会参与?
一般来说,QCC讨论要有一些行为准则,例如:
可以批评想法,但不能批评個人。
2. 唯一愚蠢的问题是没有被问到的问题。
3. 团队中的每个人都要对团队的进展负责。
4. 对他人的想法持开放态度。 收起阅读 »
优思学院|精益和六西格玛管理的演化史/发展史
原发表于优思学院知乎号
精益和六西格玛是一步一步在漫长的时间和无数前人的智慧累积而成的产物,这个发展历程可以以一个演化史的概念来论述,优思学院制作了这个视频希望可以透过一些历史发展的关键时间和事件描绘整个演化的历程,让大家易于理解。
首先,我们今天所知道的精益和六西格玛,代表了当前质量和流程改进领域的最佳实践,精益和六西格玛整个知识体系的起源和演化,可以追溯到1700年。
1700年 - 工业革命
在1700年的工业革命之前,产品是由熟练的工匠创造的。他们的工作质量是通过严格而漫长的学徒和培训过程来保证的。
工业革命后,检查被用来决定工人的产出是否可以接受。但是,由于检查不是以一种系统的方式进行的,所以它只能夠在低产量的情况下有效。
随着组织的发展,对更有效的操作的需求也在增加。
1795年 - 高斯以正态分布预测缺陷
1795年,德国数学家高斯,在试图开发缺陷的预测模型时,发现了正态分布。正态分布是今天仍然使用的最强大的统计工具之一,后来也成为了统计过程控制等工具的基础。
1911年 - 泰勒提出了科学管理
1911年,弗雷德里克‧泰勒提出了科学管理,通过优化任务的执行方式和专业分工来提高生产质量,组织可以制定标准的工作,然后由受过专门训练的人员来负责。
1913年 - 亨利‧福特建立了现代化的流水线
1913年,亨利‧福特通过增加移动平台和传送带系统改进了装配线,成为了现代化的流水线。他发现,一辆汽车在生产中停留的时间越长,其生产成本就越高。因此,他是第一个使用减少时间的浪费来降低成本的人,这也变成了后来的精益管理中的一个重要思想。
1931年 - 休哈特提出统计过程控制
1931年,沃特·休哈特指出“变异”存在于生产过程的每个方面,而我们是可以通过使用简单的统计工具如抽样和概率分析来了解变异,因此他提出了统计过程控制(SPC)和“控制图”(Control Chart)的使用,成为了质量管理和六西格玛管理的核心工具。
1950年 - 戴明博士受邀到日本
1950年,戴明博士受邀到日本向该国的总经理和工程师讲授质量心法。后来,他将一系列统计学方法引入美国产业界,他所提出的《管理十四要点》成为本世纪全面质量管理和六西格玛管理的重要理论基础。
1951年 - 朱兰出版了《质量控制手册》
1951年,另一位质量专家朱兰,出版了第一本关于质量管理最全面的著作,《质量控制手册》,他提出的质量管理学说包括质量改进三部曲、帕累托法则,成为了六西格玛改进方法论的最初形态。
1969年 - 費根堡姆提出了全面质量管理(TQM)
1969年,費根堡姆于东京举行的第一届国际质量控制会议上发表了演讲,首次提出了全面质量管理,倡导的概念包括以客户为中心、员工参与、持续的过程改进、数据的统计分析。以及将质量管理融入整个组织。
1930年-1970年 - 大野耐一等人创造出丰田生产系统
在1930年至1970年期间,大野耐一等,在戴明、朱兰、泰勒和福特等人所发展的理论基础上,开始发展一套新概念,包括减少浪费、看板、单件流、快速换模、准时生产和持续改善等等,成为了丰田生产系统,是丰田创造的高效生产管理的方法,也就成为了我们今天所说的精益生产、精益管理。
1985年 - 比尔‧史密斯发明了六西格玛方法
1985年,一位摩托罗拉的工程师——比尔‧史密斯,在寻找消除缺陷的实用方法時,开发了 "测量、分析、改进和控制 “的阶段性问题解决过程,就是后来的六西格玛过程模型,比尔‧史密斯也因此被称为六西格玛之父。
1988年 - 迈克尔‧哈里奠定了六西格玛方法论和管理架构
1988年,迈克尔-哈里将武术术语引入六西格玛,以”黑带”描述一个在六西格玛方法上达到的一定技能水平的人。同年,摩托罗拉责成哈里在整个公司推广六西格玛,从那时起,六西格玛不再是一个只由工程师使用的工具。摩托罗拉公司获得巨大财务节约的消息很快就传开了,其他公司也很快开始复制摩托罗拉的方法。
1990年 - 《改变世界的机器》一书出版
《改变世界的机器》在1990年出版,作者詹姆斯·P·沃麦克,丹尼尔·T·琼斯等在书中提出:真正过剩的是缺乏竞争力的大量生产方式的生产能力,而具有竞争力的精益生产方式的生产能力是严重缺乏的。丹尼尔·T·琼斯在2021年亦因此获得了国际精益六西格玛研究所(ILSSI)的终身成就奖。
1995年 - 杰克‧韦尔奇把六西格玛发扬光大
1995年,通用电气的首席执行官的杰克-韦尔奇,在了解到六西格玛有可能大幅节约成本后,在1995年10月,他改变了对整个通用电气的激励计划,60%的奖金与财务状况挂钩,40%与六西格玛结果挂钩。到1998年年底,公司至少是绿带的人才会被考虑担任管理职位。
2016年 - ILSSI 国际精益六西格玛研究所成立
随着精益和六西格玛的应用成果越来越明显,无数相关的培训机构前仆后继地出现,2016年,国际精益六西格玛研究所正式成立,每年举行国际性的研讨会,为不同的培训机构订立培训和考核标准,成为国际上最重要的认证和推动组织之一。
而优思学院是唯一获得国际精益六西格玛研究所认可的,以中文为培训语言的发证机构。
收起阅读 »
精益和六西格玛是一步一步在漫长的时间和无数前人的智慧累积而成的产物,这个发展历程可以以一个演化史的概念来论述,优思学院制作了这个视频希望可以透过一些历史发展的关键时间和事件描绘整个演化的历程,让大家易于理解。
首先,我们今天所知道的精益和六西格玛,代表了当前质量和流程改进领域的最佳实践,精益和六西格玛整个知识体系的起源和演化,可以追溯到1700年。
1700年 - 工业革命
在1700年的工业革命之前,产品是由熟练的工匠创造的。他们的工作质量是通过严格而漫长的学徒和培训过程来保证的。
工业革命后,检查被用来决定工人的产出是否可以接受。但是,由于检查不是以一种系统的方式进行的,所以它只能夠在低产量的情况下有效。
随着组织的发展,对更有效的操作的需求也在增加。
1795年 - 高斯以正态分布预测缺陷
1795年,德国数学家高斯,在试图开发缺陷的预测模型时,发现了正态分布。正态分布是今天仍然使用的最强大的统计工具之一,后来也成为了统计过程控制等工具的基础。
1911年 - 泰勒提出了科学管理
1911年,弗雷德里克‧泰勒提出了科学管理,通过优化任务的执行方式和专业分工来提高生产质量,组织可以制定标准的工作,然后由受过专门训练的人员来负责。
1913年 - 亨利‧福特建立了现代化的流水线
1913年,亨利‧福特通过增加移动平台和传送带系统改进了装配线,成为了现代化的流水线。他发现,一辆汽车在生产中停留的时间越长,其生产成本就越高。因此,他是第一个使用减少时间的浪费来降低成本的人,这也变成了后来的精益管理中的一个重要思想。
1931年 - 休哈特提出统计过程控制
1931年,沃特·休哈特指出“变异”存在于生产过程的每个方面,而我们是可以通过使用简单的统计工具如抽样和概率分析来了解变异,因此他提出了统计过程控制(SPC)和“控制图”(Control Chart)的使用,成为了质量管理和六西格玛管理的核心工具。
1950年 - 戴明博士受邀到日本
1950年,戴明博士受邀到日本向该国的总经理和工程师讲授质量心法。后来,他将一系列统计学方法引入美国产业界,他所提出的《管理十四要点》成为本世纪全面质量管理和六西格玛管理的重要理论基础。
1951年 - 朱兰出版了《质量控制手册》
1951年,另一位质量专家朱兰,出版了第一本关于质量管理最全面的著作,《质量控制手册》,他提出的质量管理学说包括质量改进三部曲、帕累托法则,成为了六西格玛改进方法论的最初形态。
1969年 - 費根堡姆提出了全面质量管理(TQM)
1969年,費根堡姆于东京举行的第一届国际质量控制会议上发表了演讲,首次提出了全面质量管理,倡导的概念包括以客户为中心、员工参与、持续的过程改进、数据的统计分析。以及将质量管理融入整个组织。
1930年-1970年 - 大野耐一等人创造出丰田生产系统
在1930年至1970年期间,大野耐一等,在戴明、朱兰、泰勒和福特等人所发展的理论基础上,开始发展一套新概念,包括减少浪费、看板、单件流、快速换模、准时生产和持续改善等等,成为了丰田生产系统,是丰田创造的高效生产管理的方法,也就成为了我们今天所说的精益生产、精益管理。
1985年 - 比尔‧史密斯发明了六西格玛方法
1985年,一位摩托罗拉的工程师——比尔‧史密斯,在寻找消除缺陷的实用方法時,开发了 "测量、分析、改进和控制 “的阶段性问题解决过程,就是后来的六西格玛过程模型,比尔‧史密斯也因此被称为六西格玛之父。
1988年 - 迈克尔‧哈里奠定了六西格玛方法论和管理架构
1988年,迈克尔-哈里将武术术语引入六西格玛,以”黑带”描述一个在六西格玛方法上达到的一定技能水平的人。同年,摩托罗拉责成哈里在整个公司推广六西格玛,从那时起,六西格玛不再是一个只由工程师使用的工具。摩托罗拉公司获得巨大财务节约的消息很快就传开了,其他公司也很快开始复制摩托罗拉的方法。
1990年 - 《改变世界的机器》一书出版
《改变世界的机器》在1990年出版,作者詹姆斯·P·沃麦克,丹尼尔·T·琼斯等在书中提出:真正过剩的是缺乏竞争力的大量生产方式的生产能力,而具有竞争力的精益生产方式的生产能力是严重缺乏的。丹尼尔·T·琼斯在2021年亦因此获得了国际精益六西格玛研究所(ILSSI)的终身成就奖。
1995年 - 杰克‧韦尔奇把六西格玛发扬光大
1995年,通用电气的首席执行官的杰克-韦尔奇,在了解到六西格玛有可能大幅节约成本后,在1995年10月,他改变了对整个通用电气的激励计划,60%的奖金与财务状况挂钩,40%与六西格玛结果挂钩。到1998年年底,公司至少是绿带的人才会被考虑担任管理职位。
2016年 - ILSSI 国际精益六西格玛研究所成立
随着精益和六西格玛的应用成果越来越明显,无数相关的培训机构前仆后继地出现,2016年,国际精益六西格玛研究所正式成立,每年举行国际性的研讨会,为不同的培训机构订立培训和考核标准,成为国际上最重要的认证和推动组织之一。
而优思学院是唯一获得国际精益六西格玛研究所认可的,以中文为培训语言的发证机构。
收起阅读 »
汽车行业准则:自信地采用 AIAG-VDA FMEA 方法
失效模式和效应分析(FMEA)是一种常见方法,用于制造和工程行业中找出设计、制造、装配过程、产品或服务中所有可能出现的差错。
尽管起源于军队,但随着时间推移,汽车行业已制定了 FMEA 的相关标准。因此,汽车行业的风险分析最佳实践已被许多其他行业采用并持续遵循。
多年来,汽车行业质量标准准则由两家权威组织制定:位于美国的汽车工业行动集团(AIAG)和位于德国的汽车工业协议(VDA)。
随着经济日益全球化,使得制造商从世界各地采购耗材和零件变得前所未有的简单。但是,一个行业内采用两套 FMEA 方法无疑会使效率降低,影响发展进程。例如,同时服务于北美和德国制造商的供应商,需要使用不同的标准对相同的零件进行评估,具体取决于零件的使用地区。同样,当制造商审核不同供应商时,不得不根据其地理位置使用不同的评分系统。这使得供应商比较变得既棘手又耗时,更重要的是,评估风险时更是如此!
总之,使用两套“标准”会导致混乱,并给全球供应商和制造商在产品开发和过程改进活动中,增加复杂性。
AIAG-VDA FMEA 关键更改
2019年,美国 AIAG 和德国 VDA 合作推出 FMEA 流程的标准化版本(强调预防并优先降低风险),为汽车行业的供应商提供一致的指南和准则。结果就是一个评分表,可满足整个行业中的制造商需求,从而减轻混乱的风险并减少重复工作。有了这套国际通用的准则,供应商只需管理一个单一的 FMEA 流程,即可满足世界各地所有客户的需求和期望。
相较于以前的区域手册(问题的严重性、发生频率和可检测性的权重相同),新的评分框架建立了一个等级体系。也就是说,问题的严重性将占据最大的权重,然后是发生的频率,最后是可检测性。换言之,新方法优先考虑严重问题,即使它们发生的频率相对较低并且易于检测;或者是危险性较低的问题,这些问题的发生可能会更频繁,或者更难被发现。
AIAG 与 VDA 合作为 FMEA 开发建立了全新的 7 步法,这 7 步可以分为三类。
步骤 1 至 3 与系统分析有关:
规划和准备
结构分析
功能分析
步骤 4 至 6 专注于失效分析和风险缓解:
失效分析
风险分析
优化
步骤 7 也是最后一步,将通过记录结果来解决风险沟通这个问题。
以下是设计失效模式效应分析(DFMEA)模板的预览,可在 Minitab Workspace® 和 Minitab EngageTM 中获得,是为支持最新的 AIAG-VDA FMEA 框架而创建。过程失效模式效应分析(PMFEA)模板也可在 Minitab Workspace® 和 Minitab EngageTM 中获得。请注意,虽然使用 DFMEA 和 PMFEA 在方法上存在显著差异,但两者都结合了 AIAG-VDA FMEA 7 步法。
Minitab 的 AIAG-VDA FMEA 模板如何为您提供帮助
在实施最新 AIAG-VDA FMEA 方法时,使用 FMEA 的汽车供应商必须考虑周全和彻底,同时要注意其修订后的评分框架以及更改后的方法和术语。
全面更新 FMEA 需要时间、理解和投入,但是利用 Minitab Workspace® 和 Minitab EngageTM 提供的设计专业的 DFMEA 和 PFMEA 表单模板,在确保您的 FMEA 与最新的行业标准保持一致时,您可以自信地更新您的风险分析过程。 收起阅读 »
尽管起源于军队,但随着时间推移,汽车行业已制定了 FMEA 的相关标准。因此,汽车行业的风险分析最佳实践已被许多其他行业采用并持续遵循。
多年来,汽车行业质量标准准则由两家权威组织制定:位于美国的汽车工业行动集团(AIAG)和位于德国的汽车工业协议(VDA)。
随着经济日益全球化,使得制造商从世界各地采购耗材和零件变得前所未有的简单。但是,一个行业内采用两套 FMEA 方法无疑会使效率降低,影响发展进程。例如,同时服务于北美和德国制造商的供应商,需要使用不同的标准对相同的零件进行评估,具体取决于零件的使用地区。同样,当制造商审核不同供应商时,不得不根据其地理位置使用不同的评分系统。这使得供应商比较变得既棘手又耗时,更重要的是,评估风险时更是如此!
总之,使用两套“标准”会导致混乱,并给全球供应商和制造商在产品开发和过程改进活动中,增加复杂性。
AIAG-VDA FMEA 关键更改
2019年,美国 AIAG 和德国 VDA 合作推出 FMEA 流程的标准化版本(强调预防并优先降低风险),为汽车行业的供应商提供一致的指南和准则。结果就是一个评分表,可满足整个行业中的制造商需求,从而减轻混乱的风险并减少重复工作。有了这套国际通用的准则,供应商只需管理一个单一的 FMEA 流程,即可满足世界各地所有客户的需求和期望。
相较于以前的区域手册(问题的严重性、发生频率和可检测性的权重相同),新的评分框架建立了一个等级体系。也就是说,问题的严重性将占据最大的权重,然后是发生的频率,最后是可检测性。换言之,新方法优先考虑严重问题,即使它们发生的频率相对较低并且易于检测;或者是危险性较低的问题,这些问题的发生可能会更频繁,或者更难被发现。
AIAG 与 VDA 合作为 FMEA 开发建立了全新的 7 步法,这 7 步可以分为三类。
步骤 1 至 3 与系统分析有关:
规划和准备
结构分析
功能分析
步骤 4 至 6 专注于失效分析和风险缓解:
失效分析
风险分析
优化
步骤 7 也是最后一步,将通过记录结果来解决风险沟通这个问题。
以下是设计失效模式效应分析(DFMEA)模板的预览,可在 Minitab Workspace® 和 Minitab EngageTM 中获得,是为支持最新的 AIAG-VDA FMEA 框架而创建。过程失效模式效应分析(PMFEA)模板也可在 Minitab Workspace® 和 Minitab EngageTM 中获得。请注意,虽然使用 DFMEA 和 PMFEA 在方法上存在显著差异,但两者都结合了 AIAG-VDA FMEA 7 步法。
Minitab 的 AIAG-VDA FMEA 模板如何为您提供帮助
在实施最新 AIAG-VDA FMEA 方法时,使用 FMEA 的汽车供应商必须考虑周全和彻底,同时要注意其修订后的评分框架以及更改后的方法和术语。
全面更新 FMEA 需要时间、理解和投入,但是利用 Minitab Workspace® 和 Minitab EngageTM 提供的设计专业的 DFMEA 和 PFMEA 表单模板,在确保您的 FMEA 与最新的行业标准保持一致时,您可以自信地更新您的风险分析过程。 收起阅读 »
优思学院|准时化生产(JIT)是什么?
原发表于优思学院知乎号
准时化生产的关键是刚刚及时满足客户的需求,而不是制造大量产品出来然后希望能够销售出去的概念,目标是减少、甚至消除从原材料的投入到生产的整个过程中的库存(包括WIP和成品),建立起少浪费和有效的生产流程。
库存的成本
库存管理在任何企业中都是一个关键部分,因为它可以决定企业的整体经营和财务状况。囤积产品或者物料的库存雖然可以让你的企业随时满足客户的需求,但这也需要更大的存储空间,并会有盗窃、过期或变质的风险,这些都会给企业带来巨大的成本,甚至可以抹去公司大部分的營业額。
没有通用的库存管理方法,根据你的制造企业所处的行业,你可以采用任何一种不同类型的库存管理,但最常见的方法还是准时化生产是JIT(Just In Time)。
准时化生产JIT的起源
对生产和库存管理有丰富知识的人都会知道,JIT起源于日本。日本采用这种技术通常归因于二战后日本的经济状况,当时日本正在重建其工业。
战后的日本在许多方面都有不足。它缺乏现金,以至于不同的行业无法使用哪怕是普通的方法来资助一个大型的生产。这个国家也缺乏空间,这使得建造更大的仓库来容纳更大的生产规模成为不可能完成的任务。空间的缺乏也意味着日本是资源匮乏的,或者说,由于没有太多的资源或供应商,工业必须从其他地方获得原材料。这个国家也缺乏劳动力。劳动密集型的产业发现很难重建。
这些资源的缺乏促使工业界精简生产流程,确保很少浪费。他们的生产和仓储规模很小,只存放最低水平的库存。这种方法后来得到了进一步的发展,并在20世纪70年代由丰田汽车公司带来了名声。丰田官网图片丰田生产系统--JIT原则
丰田汽车公司对JIT方法的采用和进一步发展,使这家汽车制造商成为高效生产的标杆。JIT方法现在也被称为丰田生产系统或全球应用的精益生产系统。
丰田生产系统建立在 "通过消除浪费使生产效率最大化 "的原则之上。它只是在需要的时候,只生产需要的东西。因此,驱动生产的是客户的需求。项目的生产是基于实际的订单。
简而言之,整个过程的每个阶段都是有时间限制的,某个阶段所需的材料和用品的采购只有在它们可以准确地交付给生产时才进行。因此,所有的资源都在需要的时候准确地交付。在生产的任何阶段,都不需要保留库存。丰田生产模式的官方介绍只做 "需要的东西,在需要的时候,按需要的数量"。
通过完全消除生产线上的浪费、不一致和不合理的要求(在日语中分别称为Muda、Mura、Muri),有效地生产优质产品。
为了尽快完成客户的订单,在最短的时间内有效地制造车辆,要坚持以下几点:
当收到车辆订单时,必须尽快向车辆生产线的起点发出生产指令。
2. 装配线必须储备所需数量的所有必要零件,以便可以组装任何种类的订购车辆。
3. 装配线必须通过从零件生产过程(前道工序)中取回相同数量的零件来替换所用的零件。
4. 前道工序必须储备少量的各类零件,只生产操作员从下道工序取回的零件数量。 收起阅读 »
准时化生产的关键是刚刚及时满足客户的需求,而不是制造大量产品出来然后希望能够销售出去的概念,目标是减少、甚至消除从原材料的投入到生产的整个过程中的库存(包括WIP和成品),建立起少浪费和有效的生产流程。
库存的成本
库存管理在任何企业中都是一个关键部分,因为它可以决定企业的整体经营和财务状况。囤积产品或者物料的库存雖然可以让你的企业随时满足客户的需求,但这也需要更大的存储空间,并会有盗窃、过期或变质的风险,这些都会给企业带来巨大的成本,甚至可以抹去公司大部分的營业額。
没有通用的库存管理方法,根据你的制造企业所处的行业,你可以采用任何一种不同类型的库存管理,但最常见的方法还是准时化生产是JIT(Just In Time)。
准时化生产JIT的起源
对生产和库存管理有丰富知识的人都会知道,JIT起源于日本。日本采用这种技术通常归因于二战后日本的经济状况,当时日本正在重建其工业。
战后的日本在许多方面都有不足。它缺乏现金,以至于不同的行业无法使用哪怕是普通的方法来资助一个大型的生产。这个国家也缺乏空间,这使得建造更大的仓库来容纳更大的生产规模成为不可能完成的任务。空间的缺乏也意味着日本是资源匮乏的,或者说,由于没有太多的资源或供应商,工业必须从其他地方获得原材料。这个国家也缺乏劳动力。劳动密集型的产业发现很难重建。
这些资源的缺乏促使工业界精简生产流程,确保很少浪费。他们的生产和仓储规模很小,只存放最低水平的库存。这种方法后来得到了进一步的发展,并在20世纪70年代由丰田汽车公司带来了名声。丰田官网图片丰田生产系统--JIT原则
丰田汽车公司对JIT方法的采用和进一步发展,使这家汽车制造商成为高效生产的标杆。JIT方法现在也被称为丰田生产系统或全球应用的精益生产系统。
丰田生产系统建立在 "通过消除浪费使生产效率最大化 "的原则之上。它只是在需要的时候,只生产需要的东西。因此,驱动生产的是客户的需求。项目的生产是基于实际的订单。
简而言之,整个过程的每个阶段都是有时间限制的,某个阶段所需的材料和用品的采购只有在它们可以准确地交付给生产时才进行。因此,所有的资源都在需要的时候准确地交付。在生产的任何阶段,都不需要保留库存。丰田生产模式的官方介绍只做 "需要的东西,在需要的时候,按需要的数量"。
通过完全消除生产线上的浪费、不一致和不合理的要求(在日语中分别称为Muda、Mura、Muri),有效地生产优质产品。
为了尽快完成客户的订单,在最短的时间内有效地制造车辆,要坚持以下几点:
当收到车辆订单时,必须尽快向车辆生产线的起点发出生产指令。
2. 装配线必须储备所需数量的所有必要零件,以便可以组装任何种类的订购车辆。
3. 装配线必须通过从零件生产过程(前道工序)中取回相同数量的零件来替换所用的零件。
4. 前道工序必须储备少量的各类零件,只生产操作员从下道工序取回的零件数量。 收起阅读 »