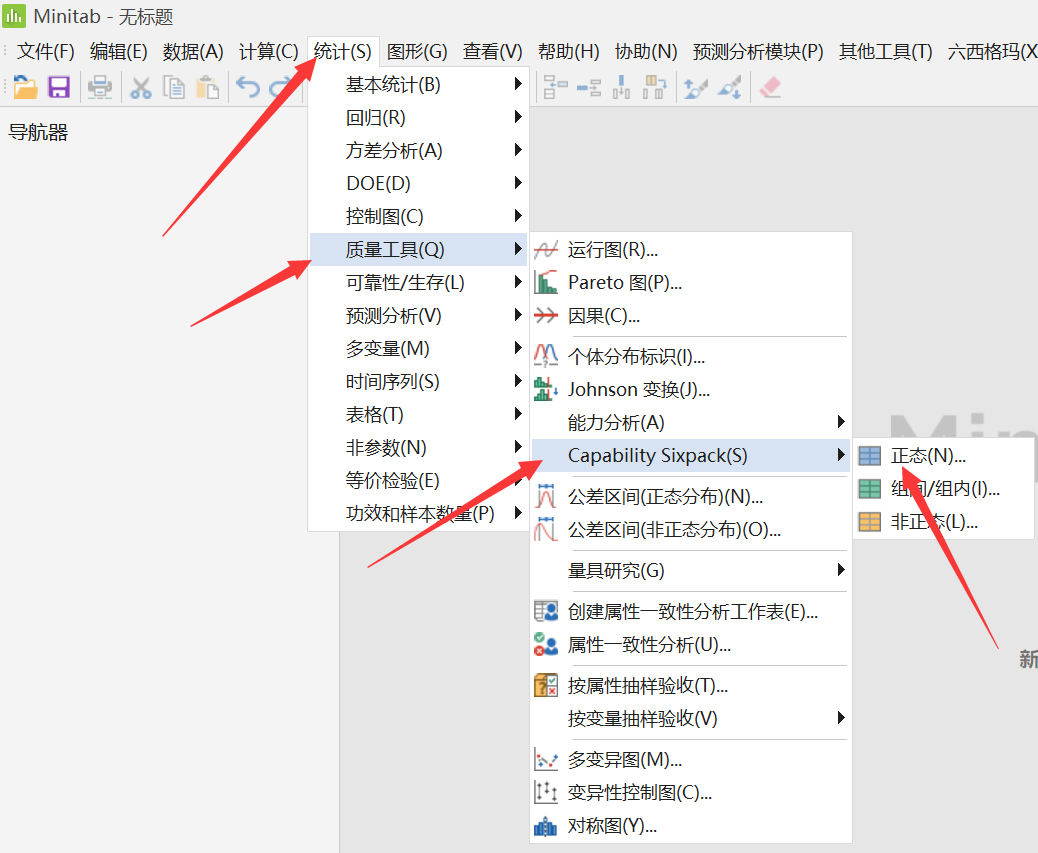
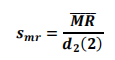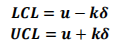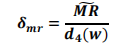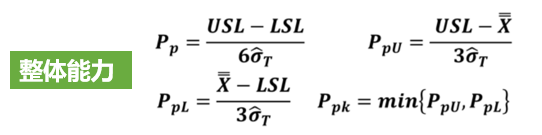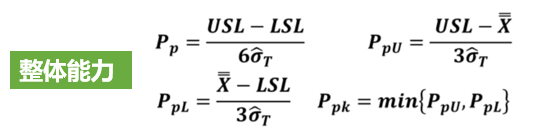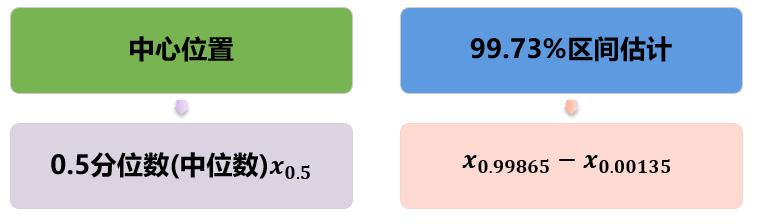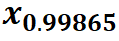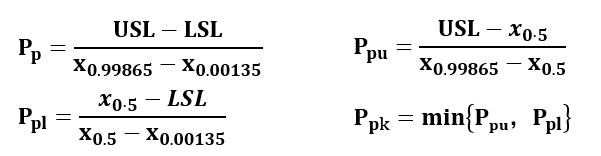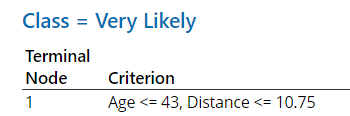SPC 之 I-MR 控制图
概述
1924 年,美国的休哈特博士应用统计数学理论将 3Sigma 原理运用于生产过程中,并发表了著名的“控制图法”,对产品特性和过程变量进行控制,开启了统计过程控制新时代。
什么是控制图
控制图指示过程何时不受控制,有助于标识是否存在特殊原因变异。如果存在特殊原因变异,则说明过程不稳定且有必要采取纠正措施。
控制图是按时间排序顺序绘制过程数据的图。大多数控制图都包括一条中心线、一个控制上限和一个控制下限。中心线表示过程均值。控制限表示过程变异。默认情况下,控制限绘制在中心线上下 3σ 的位置。
随机位于控制限内的点指示过程受控制且仅显示常见原因变异。位于控制限外部或者显示非随机模式的点指示过程不受控制且存在特殊原因变异。
如何选择合适的控制图
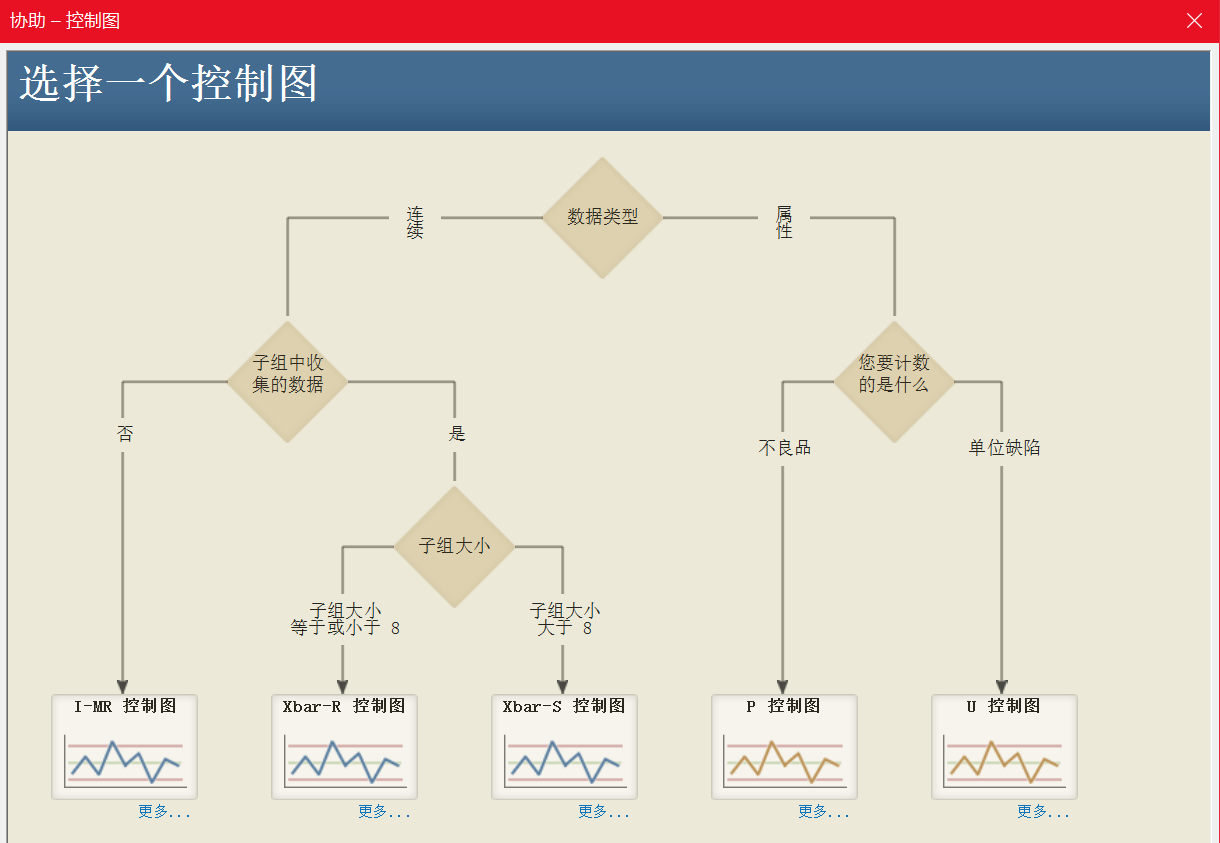
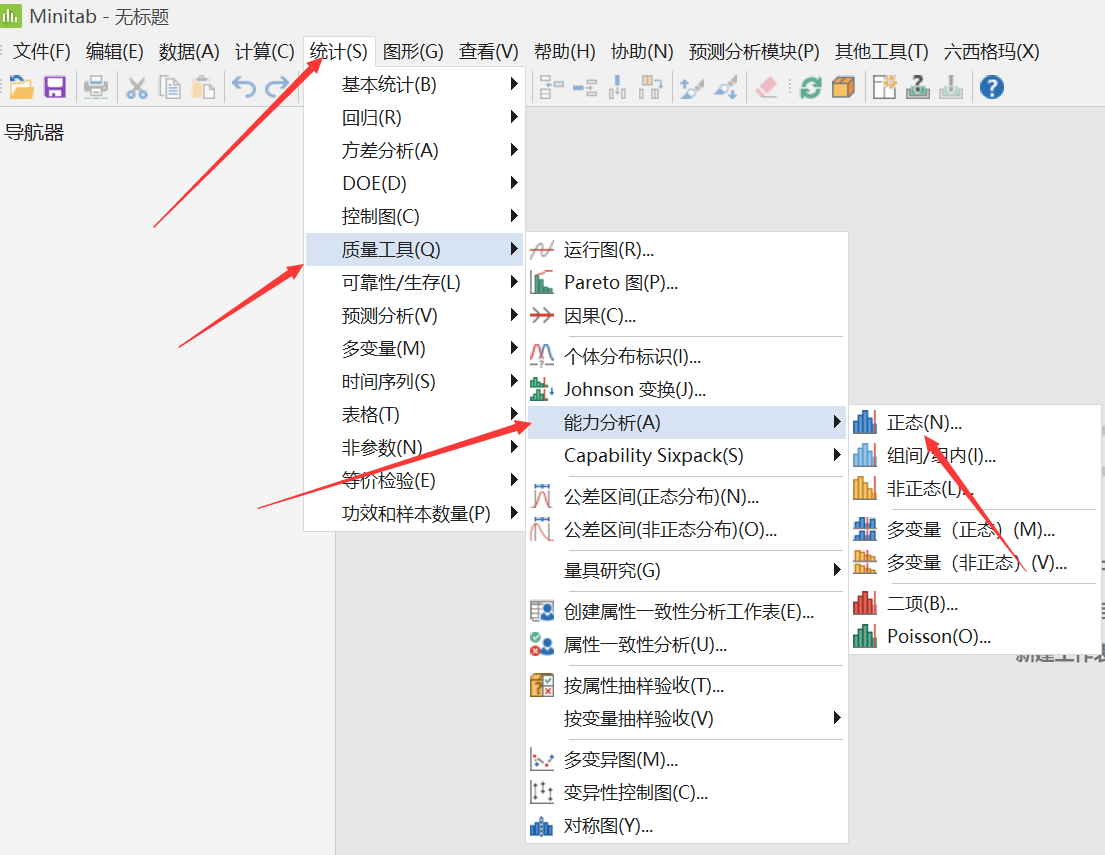
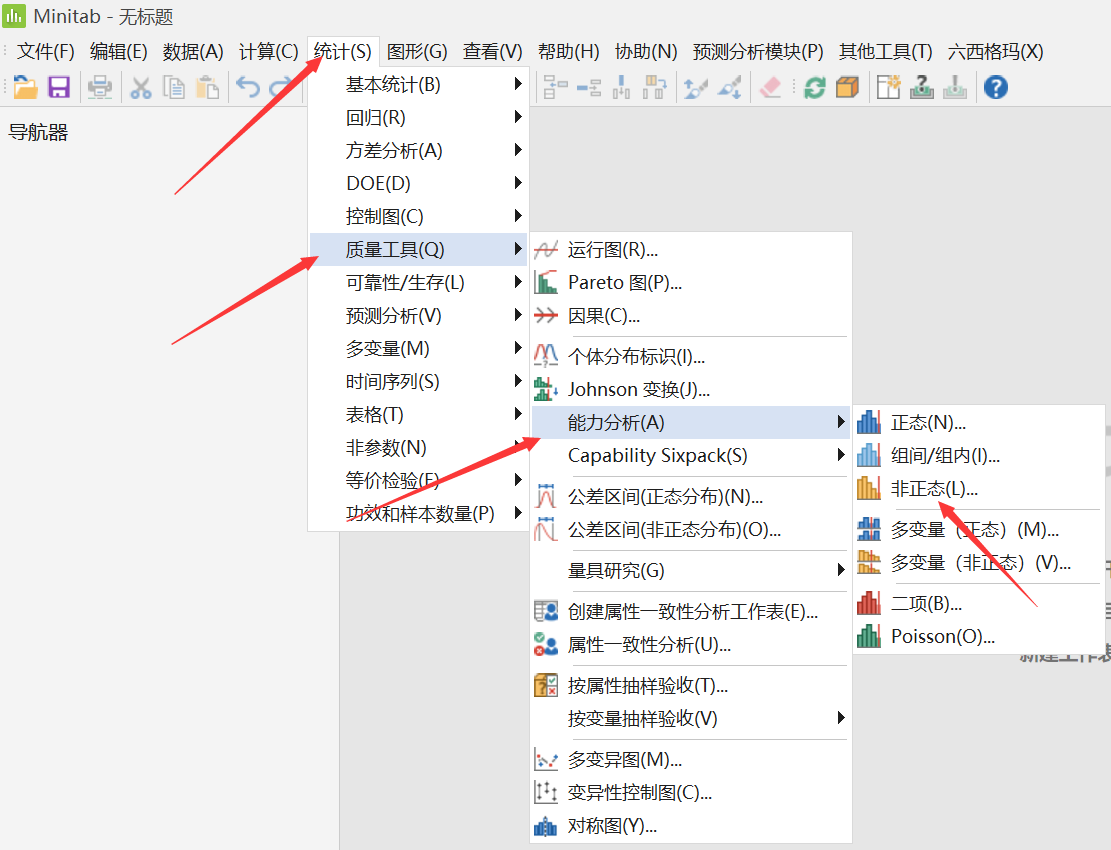
随着控制图的发展,它的类型也是越来越多,那么这时候对于使用 Minitab 的朋友来说,经常会纠结如何去选择一个合适的控制图。在 Minitab 19 中,协助菜单可以很好的帮助我们去选择一个合适的控制图。
I-MR 控制图
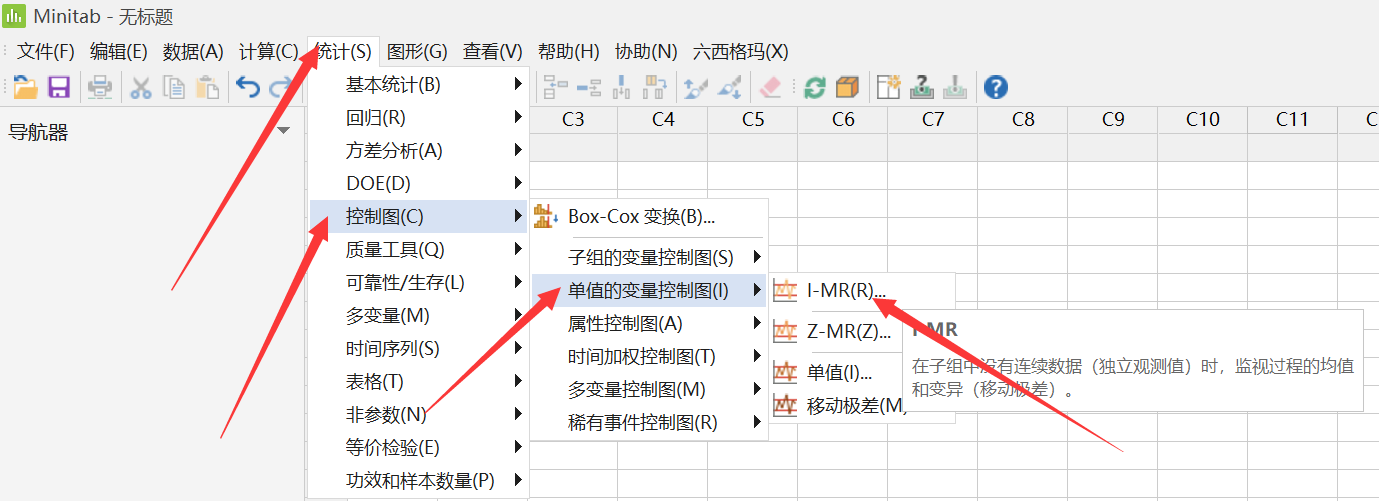
今天,我们来绘制一下 I-MR 控制图。
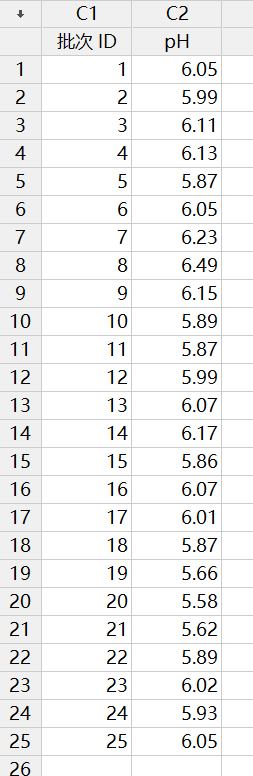
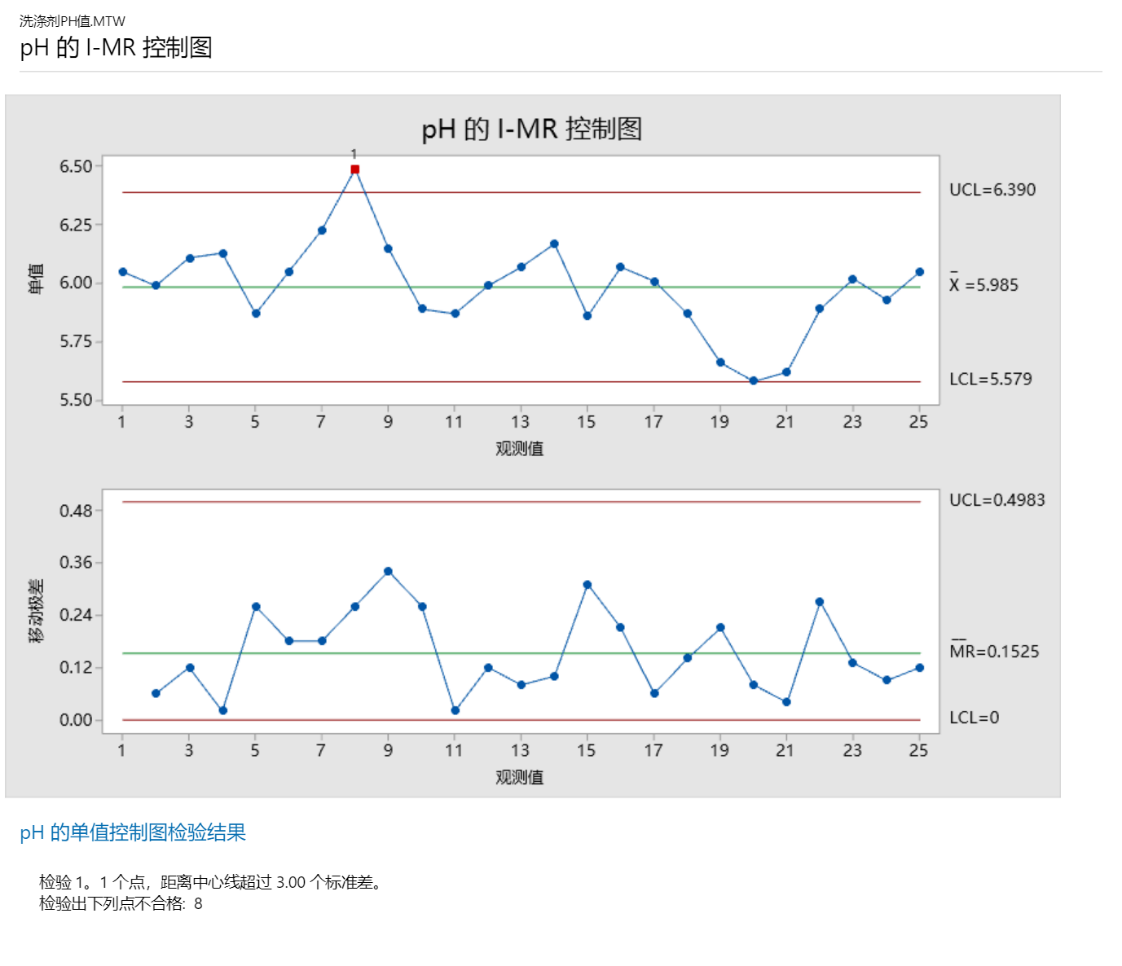
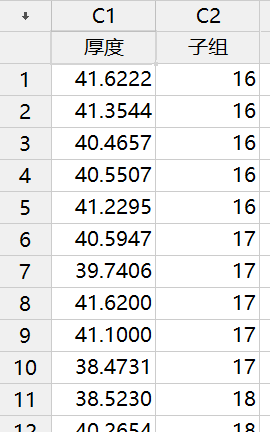
问题背景:某质量工程师监控了液体洗涤剂的生产过程,想要评估该过程是否受控制。这位工程师测量了 25 个连续批次的洗涤剂的 pH 值。
由于 pH 值的数据类型是连续型数据,而且是每批次只取一个样品(子组大小等于 1),故这位工程师创建了一张 I-MR 控制图,以监控洗涤剂的生产过程。
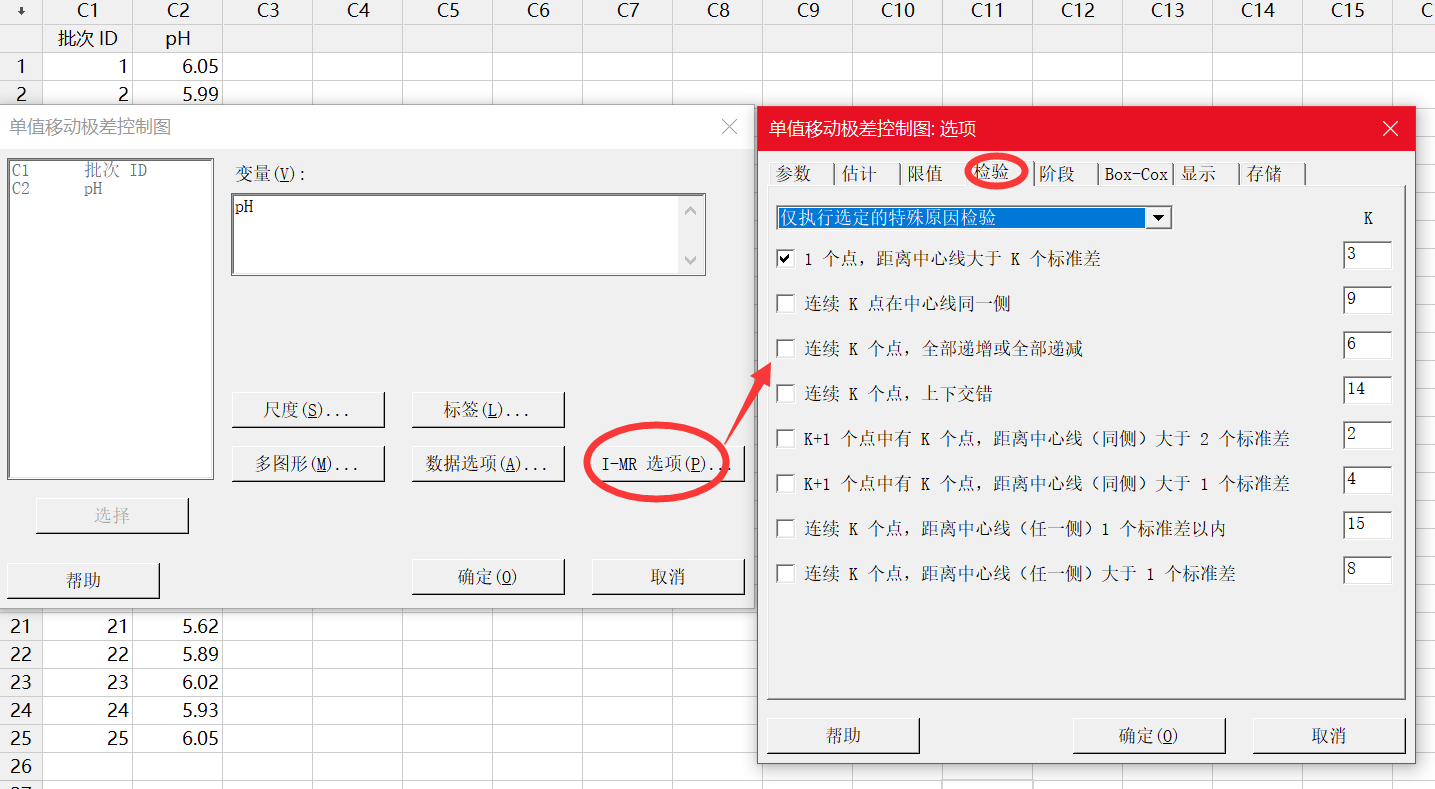
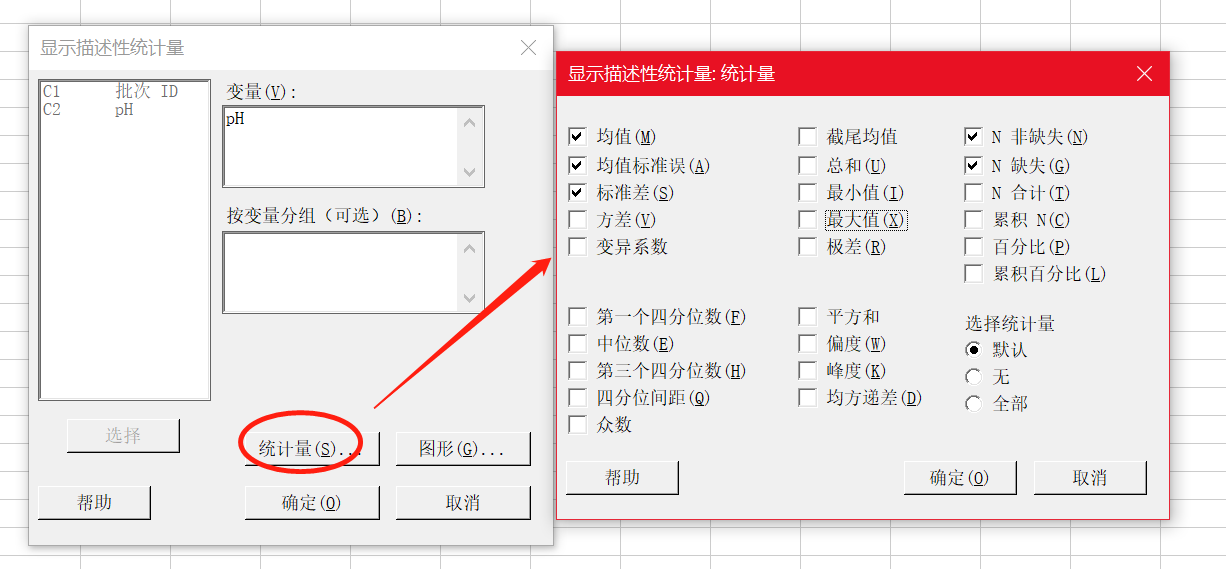
Minitab 绘制 I-MR 控制图
Minitab 结果解释
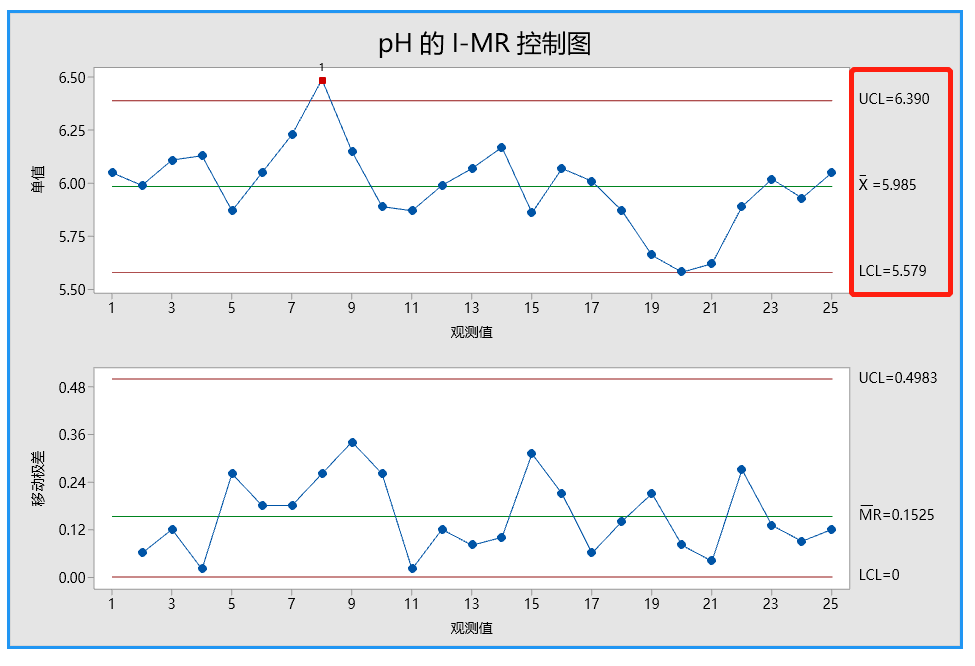
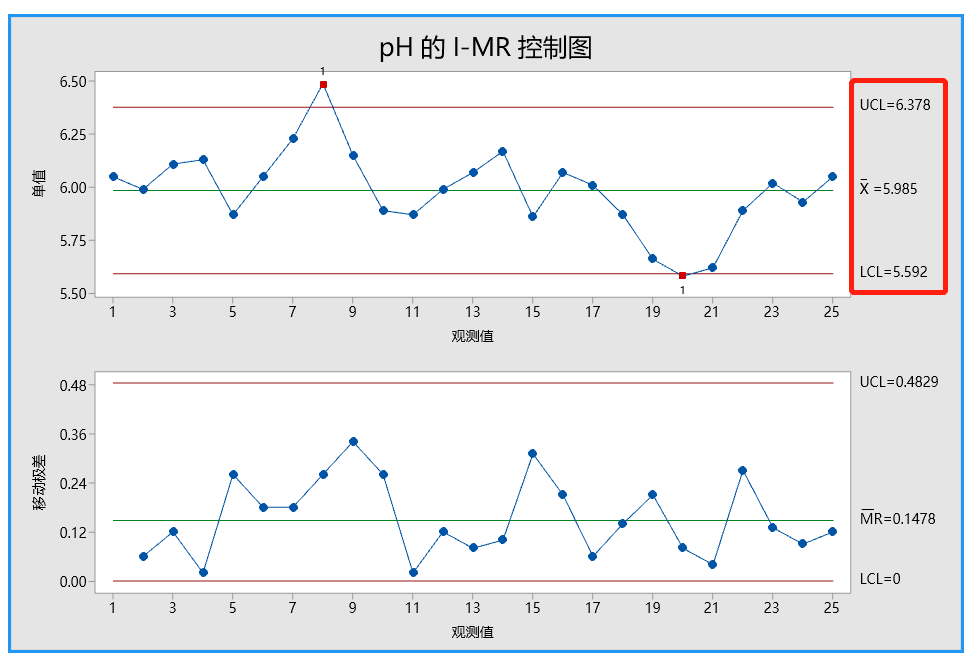
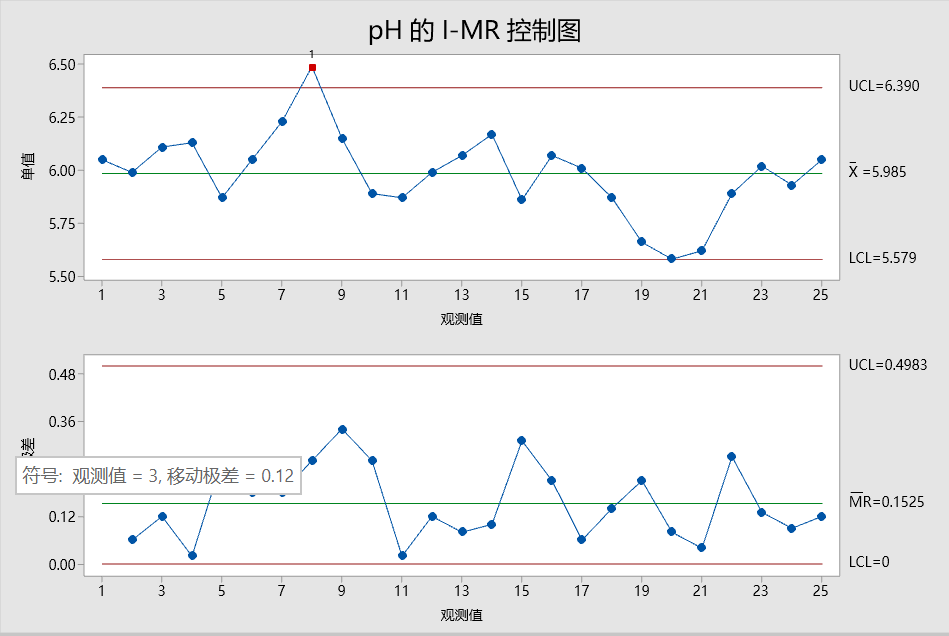
首先解释移动极差控制图(MR 控制图)以检查过程变异。没有位于控制限外部的点且所有的点都显示出随机模式。因此,过程变异受控制,质量工程师可以检查单值控制图(I 控制图)上的过程中心。
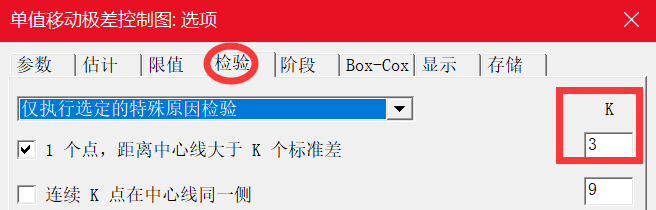
I 控制图上的一个观测值在检验 1 中失败,因为观测值在中心线上方且距离中心线超过 3个标准差。
I-MR 控制图的控制限计算(手动)
对于 I-MR 控制图,包含两张图单值控制图(I 控制图)和移动极差控制图(MR 控制图), 我们首先来认识一下这两张图形上的 X 轴、Y 轴、点和线分别表示什么含义。
一、单值控制图(I 控制图)
X 轴:批次 ID
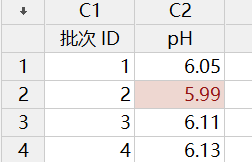
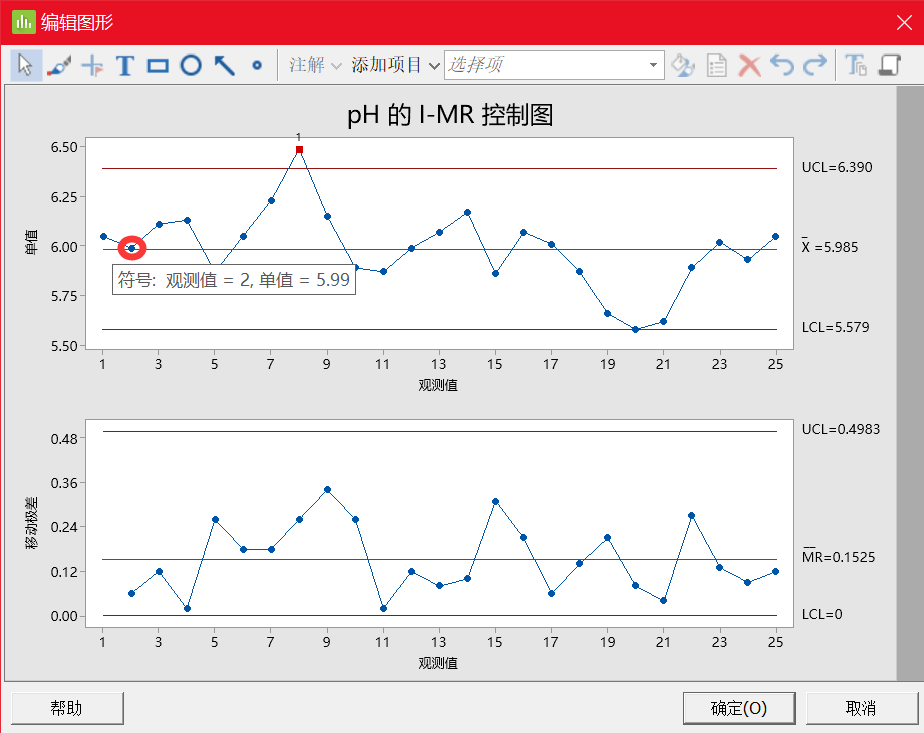
Y 轴:单值(每个批次对应的 pH 值,如单值图上的第二个点表示的是批次 2 的 pH 值)
点:单值控制图(I 控制图)上的每个标绘点是单独的观测值(如上图)。
中心线:单值控制图(I 控制图)上的中心线是过程平均值的估计值,计算如下
控制限:单值控制图(I 控制图)控制限的计算结果取决于标准差的估计方式。
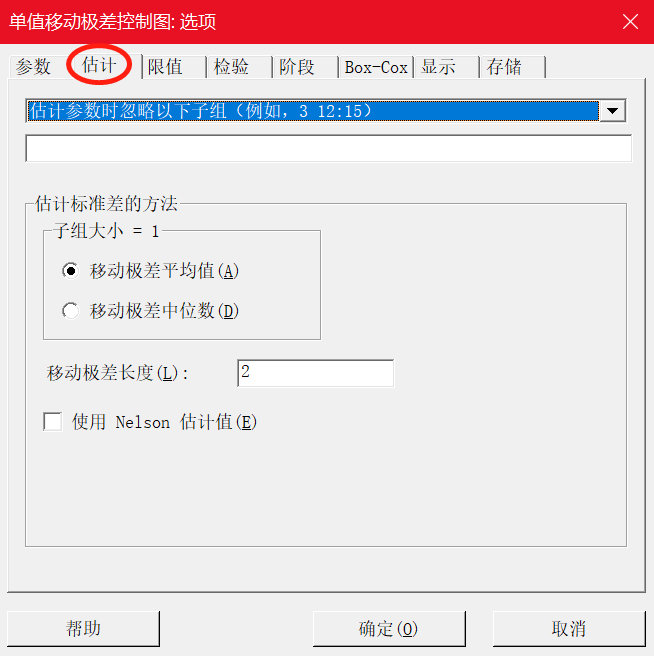
1)移动极差平均值(默认方法)-移动极差长度默认为 2
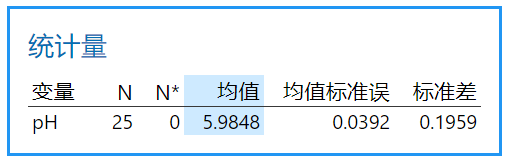
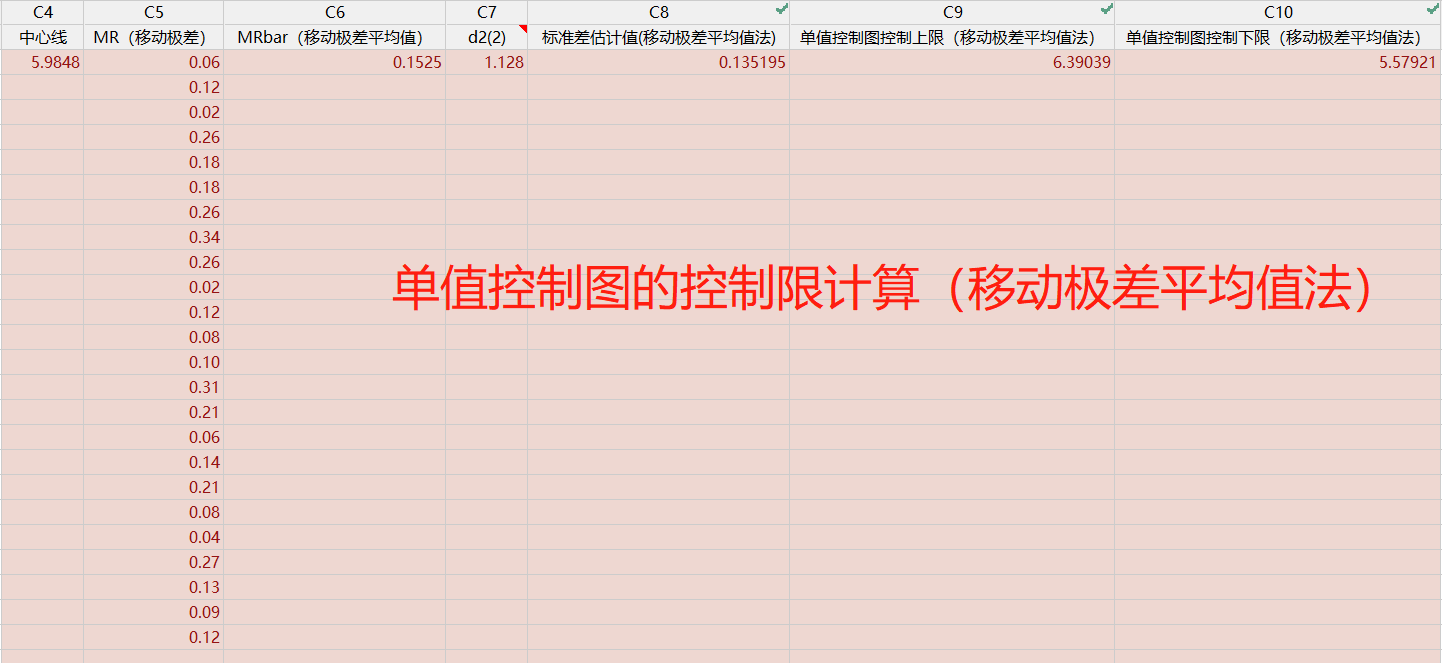
a. 计算移动极差 MR(相邻 2 个数的较大值减较小值),当前数据样本量为 25,计算得到24 个移动极差。
b. 计算这 24 个移动极差的平均值 MRbar
c. 估计标准差的公式如下:
控制限计算公式
其中 k 为检验 1 的参数。默认值为 3。
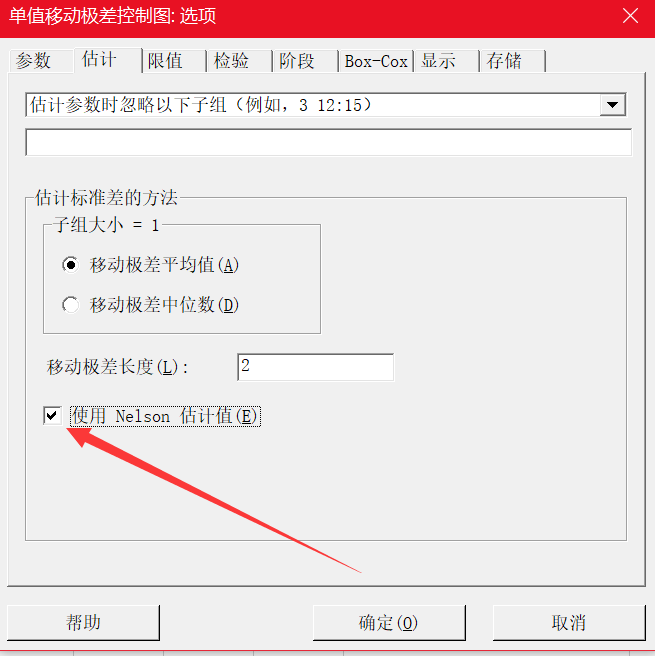
当选择默认的用移动极差平均值来估计标准差时,我们还可以勾选”使用 Nelson 估计值”。使用 Nelson 估计值可以在计算控制限时更正异常大的移动极差值。此过程与 Nelson1 提出的过程相似。Minitab 消除比移动极差平均值大 3σ 的任何移动极差值,然后重新计算移动极差平均值和控制限。
2)移动极差中位数
a. 计算移动极差
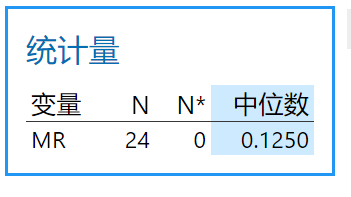
b. 计算移动极差中位数
c. 估计标准差的公式如下:
二、移动极差控制图(MR 控制图)
X 轴:批次 ID
Y 轴:移动极差(如下 MR 控制图中的第二个点是批次 2 的 pH 值 5.99 和批次 3pH 值 6.11中较大值减去较小值,结果为 0.12(6.11-5.99)
点:MR 控制图上的标绘点是移动极差(移动极差是两个或多个连续点之间差值的绝对值)。
中心线:中心线是移动极差平均值的无偏估计值 MRbar
控制上限:??? = (??(?) ⋅ ?) + (? ⋅ ??(?) ⋅ ?)
控制下限:??? = (??(?) ⋅ ?) − (? ⋅ ??(?) ⋅ ?)或 LCL=0(计算结果为负值时)
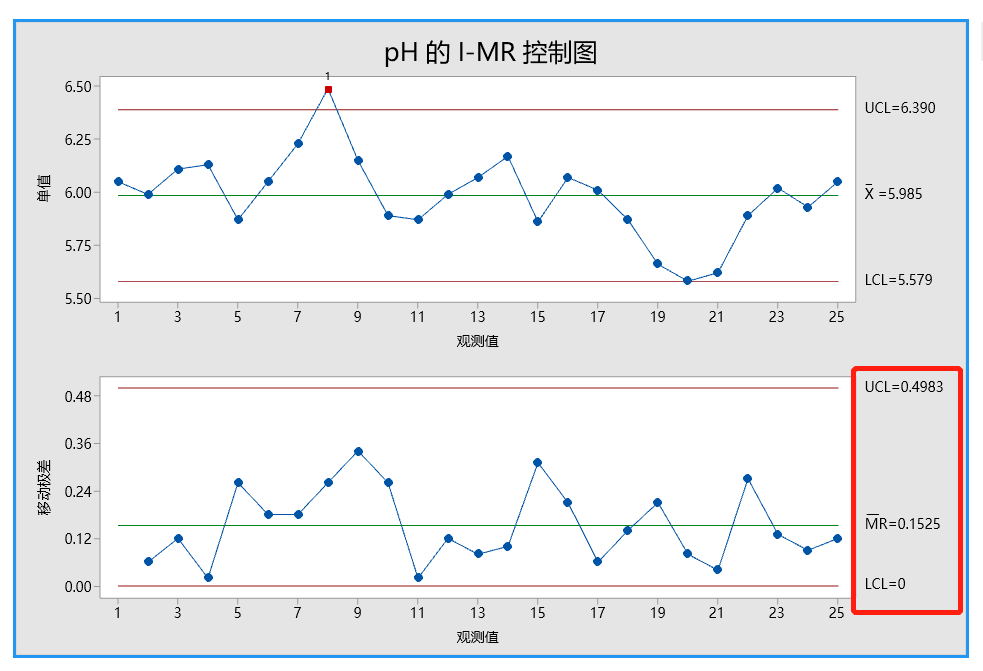
移动极差平均值法的结果
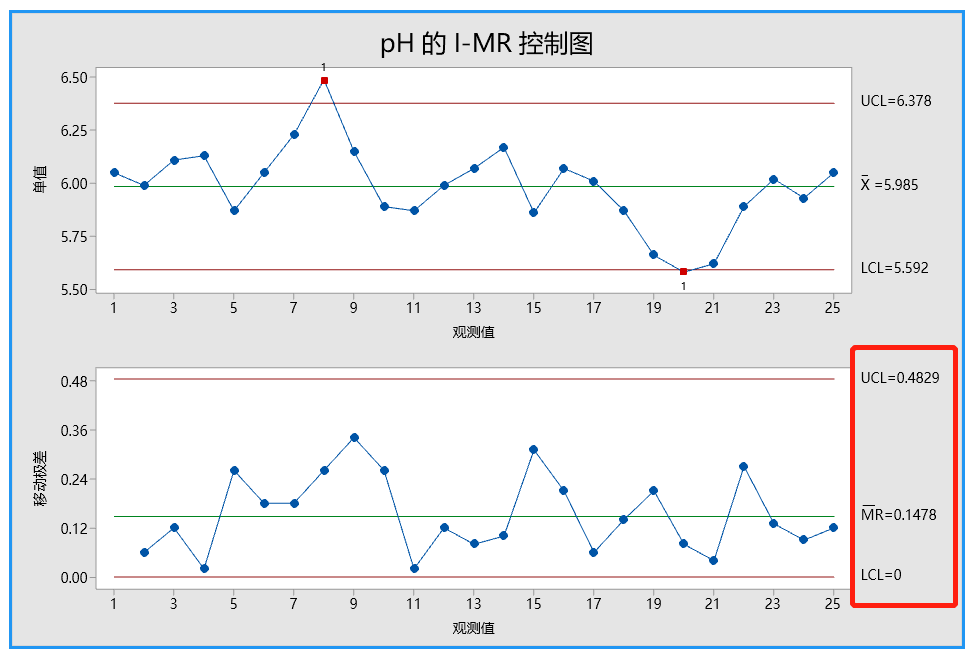
移动极差中位数法的结果
结论
手动计算的过程比较复杂,而且还可能会出错,但是有了 Minitab 的帮助,我们只需要选择好合适的控制图后,点击几下就可以高效快速的计算出对应的控制限。当然,花点时间手动计算一下这些值,能够帮助你更好的理解控制图。而且在计算的过程中,你也会发现 Minitab 的算法跟 Excel 中算法的差异,也能够发现单值控制图的控制限受到移动极差的影响,所以在分析这两张控制图时,应该先分析下面的移动极差控制图,移动极差控制图中没有异常点时,这时候分析单值控制图才是有意义的。
X 轴:批次 ID
Y 轴:移动极差(如下 MR 控制图中的第二个点是批次 2 的 pH 值 5.99 和批次3pH 值 6.11 中较大值减去较小值,结果为 0.12(6.11-5.99) 收起阅读 »
1924 年,美国的休哈特博士应用统计数学理论将 3Sigma 原理运用于生产过程中,并发表了著名的“控制图法”,对产品特性和过程变量进行控制,开启了统计过程控制新时代。
什么是控制图
控制图指示过程何时不受控制,有助于标识是否存在特殊原因变异。如果存在特殊原因变异,则说明过程不稳定且有必要采取纠正措施。
控制图是按时间排序顺序绘制过程数据的图。大多数控制图都包括一条中心线、一个控制上限和一个控制下限。中心线表示过程均值。控制限表示过程变异。默认情况下,控制限绘制在中心线上下 3σ 的位置。
随机位于控制限内的点指示过程受控制且仅显示常见原因变异。位于控制限外部或者显示非随机模式的点指示过程不受控制且存在特殊原因变异。
如何选择合适的控制图
随着控制图的发展,它的类型也是越来越多,那么这时候对于使用 Minitab 的朋友来说,经常会纠结如何去选择一个合适的控制图。在 Minitab 19 中,协助菜单可以很好的帮助我们去选择一个合适的控制图。
I-MR 控制图
今天,我们来绘制一下 I-MR 控制图。
问题背景:某质量工程师监控了液体洗涤剂的生产过程,想要评估该过程是否受控制。这位工程师测量了 25 个连续批次的洗涤剂的 pH 值。
由于 pH 值的数据类型是连续型数据,而且是每批次只取一个样品(子组大小等于 1),故这位工程师创建了一张 I-MR 控制图,以监控洗涤剂的生产过程。
Minitab 绘制 I-MR 控制图
Minitab 结果解释
首先解释移动极差控制图(MR 控制图)以检查过程变异。没有位于控制限外部的点且所有的点都显示出随机模式。因此,过程变异受控制,质量工程师可以检查单值控制图(I 控制图)上的过程中心。
I 控制图上的一个观测值在检验 1 中失败,因为观测值在中心线上方且距离中心线超过 3个标准差。
I-MR 控制图的控制限计算(手动)
对于 I-MR 控制图,包含两张图单值控制图(I 控制图)和移动极差控制图(MR 控制图), 我们首先来认识一下这两张图形上的 X 轴、Y 轴、点和线分别表示什么含义。
一、单值控制图(I 控制图)
X 轴:批次 ID
Y 轴:单值(每个批次对应的 pH 值,如单值图上的第二个点表示的是批次 2 的 pH 值)
点:单值控制图(I 控制图)上的每个标绘点是单独的观测值(如上图)。
中心线:单值控制图(I 控制图)上的中心线是过程平均值的估计值,计算如下
控制限:单值控制图(I 控制图)控制限的计算结果取决于标准差的估计方式。
1)移动极差平均值(默认方法)-移动极差长度默认为 2
a. 计算移动极差 MR(相邻 2 个数的较大值减较小值),当前数据样本量为 25,计算得到24 个移动极差。
b. 计算这 24 个移动极差的平均值 MRbar
c. 估计标准差的公式如下:
控制限计算公式
其中 k 为检验 1 的参数。默认值为 3。
当选择默认的用移动极差平均值来估计标准差时,我们还可以勾选”使用 Nelson 估计值”。使用 Nelson 估计值可以在计算控制限时更正异常大的移动极差值。此过程与 Nelson1 提出的过程相似。Minitab 消除比移动极差平均值大 3σ 的任何移动极差值,然后重新计算移动极差平均值和控制限。
2)移动极差中位数
a. 计算移动极差
b. 计算移动极差中位数
c. 估计标准差的公式如下:
二、移动极差控制图(MR 控制图)
X 轴:批次 ID
Y 轴:移动极差(如下 MR 控制图中的第二个点是批次 2 的 pH 值 5.99 和批次 3pH 值 6.11中较大值减去较小值,结果为 0.12(6.11-5.99)
点:MR 控制图上的标绘点是移动极差(移动极差是两个或多个连续点之间差值的绝对值)。
中心线:中心线是移动极差平均值的无偏估计值 MRbar
控制上限:??? = (??(?) ⋅ ?) + (? ⋅ ??(?) ⋅ ?)
控制下限:??? = (??(?) ⋅ ?) − (? ⋅ ??(?) ⋅ ?)或 LCL=0(计算结果为负值时)
移动极差平均值法的结果
移动极差中位数法的结果
结论
手动计算的过程比较复杂,而且还可能会出错,但是有了 Minitab 的帮助,我们只需要选择好合适的控制图后,点击几下就可以高效快速的计算出对应的控制限。当然,花点时间手动计算一下这些值,能够帮助你更好的理解控制图。而且在计算的过程中,你也会发现 Minitab 的算法跟 Excel 中算法的差异,也能够发现单值控制图的控制限受到移动极差的影响,所以在分析这两张控制图时,应该先分析下面的移动极差控制图,移动极差控制图中没有异常点时,这时候分析单值控制图才是有意义的。
X 轴:批次 ID
Y 轴:移动极差(如下 MR 控制图中的第二个点是批次 2 的 pH 值 5.99 和批次3pH 值 6.11 中较大值减去较小值,结果为 0.12(6.11-5.99) 收起阅读 »
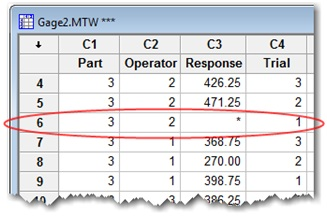
在 Minitab 中进行扩展量具 R&R 研究
量具 R&R 研究可以告诉您测量系统生成的数据是否值得信赖。遗憾的是,严格的数据要求和其他限制可能会让量具 R&R 研究难以进行分析,并可能无法解释所有重要因子。Minitab 中的扩展量具 R&R 工具能够使这些障碍成为过去。
量具 R&R 研究可以告诉您什么?
• 您的测量系统是否足够灵敏?
• 您的测量工具是否一致?
• 进行测量的人是否一致?
扩展量具 R&R 能提供哪些额外优势?
• 不仅要分析部件和操作员,还要分析多达八个其他因子。
• 甚至不完整的数据也可以进行分析(不平衡研究)。
• 包括固定或随机因子,获得更好的灵活性。
在量具 R&R 研究中包含两个以上的因子
通常,量具 R&R 研究只关注两个因子:部件和操作员。但是如果您知道其他因子也会影响您的测量系统呢?如果您不纳入这些因子,则将永远无法了解它们对测量变异性有多大影响,以及您的测量系统可能看起来比实际情况更好还是更差。Minitab 的扩展量具 R&R 能让您纳入最多八个额外的因子,用于调查并评估所有可能影响测量系统的因子。
例如
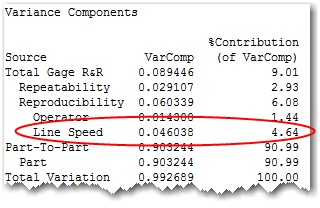
因为他们在繁忙的生产车间工作,检验人员担心生产速度的变化会影响他们的测量能力。加入生产线速度作为量具研究的因子,揭示出生产线速度变化对测量的影响甚至超出他们的预期。
以不完整或不平衡的数据进行量具 R&R
量具 R&R 研究可以要求严格的“平衡”设计,尽管实际上数据的收集通常并不完美。也许在研究中让操作员将所有部件测量相同的次数并不可行,或者可能一些测量数据已经丢失。扩展量具 R&R 允许您分析测量系统,即使有这样不平衡的数据,也无需手动计算来解释丢失的数据。
包括固定或随机因子以获取更高的灵活性
在量具研究中,如果您有意选择了一定的兴趣级别(比如最有经验和最缺乏经验的操作员),则该因子是固定的。如果您随机选择了级别来代表总体,则该因子为随机。常见量具研究会在所有因子均为随机的基础上计算结果。但将固定因子视为随机因子可能导致过度或低估其重要性。
扩展量具 R&R 允许您指明哪些因子是固定的,哪些是随机的,以便更好更妥当地评估您的测量系统。
例如
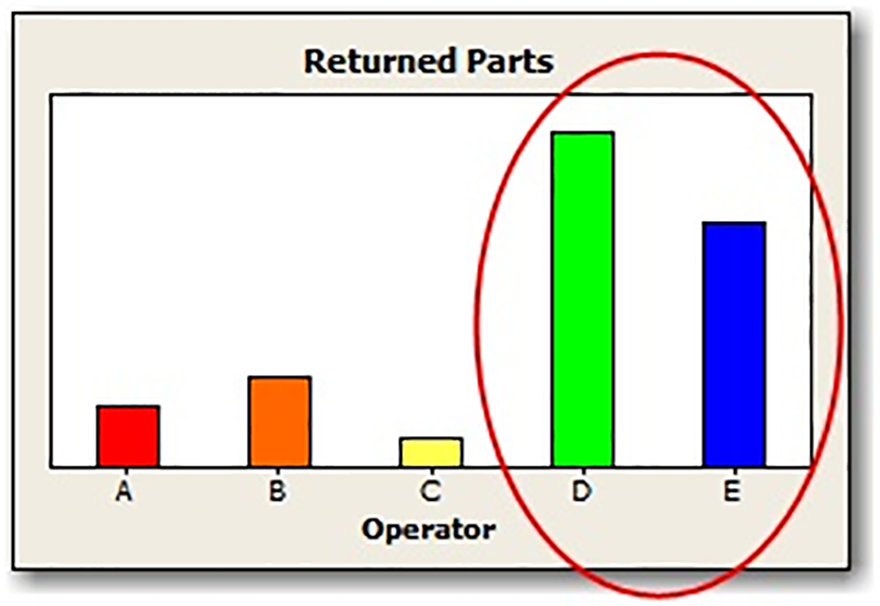
审核显示,退回精密铣削设施的大部分不合规格部件可追溯到两名经验最少的检验员。为了更好的理解该问题,质量经理希望能重点关注这些特定操作员后续的量具研究。因为人工挑选的这些操作员无法反应出随机抽样,所以在分析该研究时,经理将这一因子指定为固定因子。
MINITAB 让量具 R&R 更简单
如果您尚未利用 Minitab 的强大功能从数据中获取最大价值,请立即下载功能完备的 Minitab 30 天免费试用版。
本文最初出现在Minitab博客上。
收起阅读 »
量具 R&R 研究可以告诉您什么?
• 您的测量系统是否足够灵敏?
• 您的测量工具是否一致?
• 进行测量的人是否一致?
扩展量具 R&R 能提供哪些额外优势?
• 不仅要分析部件和操作员,还要分析多达八个其他因子。
• 甚至不完整的数据也可以进行分析(不平衡研究)。
• 包括固定或随机因子,获得更好的灵活性。
在量具 R&R 研究中包含两个以上的因子
通常,量具 R&R 研究只关注两个因子:部件和操作员。但是如果您知道其他因子也会影响您的测量系统呢?如果您不纳入这些因子,则将永远无法了解它们对测量变异性有多大影响,以及您的测量系统可能看起来比实际情况更好还是更差。Minitab 的扩展量具 R&R 能让您纳入最多八个额外的因子,用于调查并评估所有可能影响测量系统的因子。
例如
因为他们在繁忙的生产车间工作,检验人员担心生产速度的变化会影响他们的测量能力。加入生产线速度作为量具研究的因子,揭示出生产线速度变化对测量的影响甚至超出他们的预期。
以不完整或不平衡的数据进行量具 R&R
量具 R&R 研究可以要求严格的“平衡”设计,尽管实际上数据的收集通常并不完美。也许在研究中让操作员将所有部件测量相同的次数并不可行,或者可能一些测量数据已经丢失。扩展量具 R&R 允许您分析测量系统,即使有这样不平衡的数据,也无需手动计算来解释丢失的数据。
包括固定或随机因子以获取更高的灵活性
在量具研究中,如果您有意选择了一定的兴趣级别(比如最有经验和最缺乏经验的操作员),则该因子是固定的。如果您随机选择了级别来代表总体,则该因子为随机。常见量具研究会在所有因子均为随机的基础上计算结果。但将固定因子视为随机因子可能导致过度或低估其重要性。
扩展量具 R&R 允许您指明哪些因子是固定的,哪些是随机的,以便更好更妥当地评估您的测量系统。
例如
审核显示,退回精密铣削设施的大部分不合规格部件可追溯到两名经验最少的检验员。为了更好的理解该问题,质量经理希望能重点关注这些特定操作员后续的量具研究。因为人工挑选的这些操作员无法反应出随机抽样,所以在分析该研究时,经理将这一因子指定为固定因子。
MINITAB 让量具 R&R 更简单
如果您尚未利用 Minitab 的强大功能从数据中获取最大价值,请立即下载功能完备的 Minitab 30 天免费试用版。
本文最初出现在Minitab博客上。
收起阅读 »
样本量大于30就可以认为是正态分布吗?你可能对中心极限定理有误区!
我经常会被问到这么一个问题:样本量多大就不用进行正态性检验了。殊不知,这问题的本身就是错误的,并不是样本大,就一定要服从正态分布。我们可以轻易举出一个反例来说明这个问题。比方说就用1-1000这一千个(甚至更多)自然数,组成一个样本,那么这个样本的分布就不是正态分布,因为1-1000服从的是均匀分布。另外,数据的分布基于形成的机理,有的分布天生就非正态(如寿命数据)。
但有些朋友,并不觉得这是一个错误的问题,甚至在他们的学习中还流传着这么一个说法:样本量大于30就可以认为是服从正态分布。当你向他问为什么的时候,会得到一个专业的解释——中心极限定理。
中心极限定理
中心极限定理(Central Limit Theorem)是统计学中最重要的结论之一。在这里,我并不想给出中心极限定理专业的定义,只需要了解它告诉我们:来自某总体的一个样本,无论该总体服从什么分布,只要样本容量足够大,其样本均值都近似服从正态分布。
请注意这里的说法:“样本均值“近似正态,而不是样本本身服从正态(不是说你抽了30个样品组成的样本数据就正态)。这里又有一个大家疑惑的地方,样本容量足够大,多大才是足够大?这个问题的答案和总体分布的形状相关,如果样本本是来自近似对称分布的总体,那么当样本量取相当小(如样本量取5)的值的时候,正态逼近的结果也会非常好。然后,如果总体的分布严重倾斜,则样本量必须取相当大的值。根据检验,对于大多数总体来说,样本容量取30或者更大,就足以得到令人满意的正态逼近结果。我想这可能就是错误认为样本量大于30就认为是正态分布的出处了。
模拟掷骰子展示中心极限定理
为了展示中心极限定理,模拟多次投掷骰子来说明。
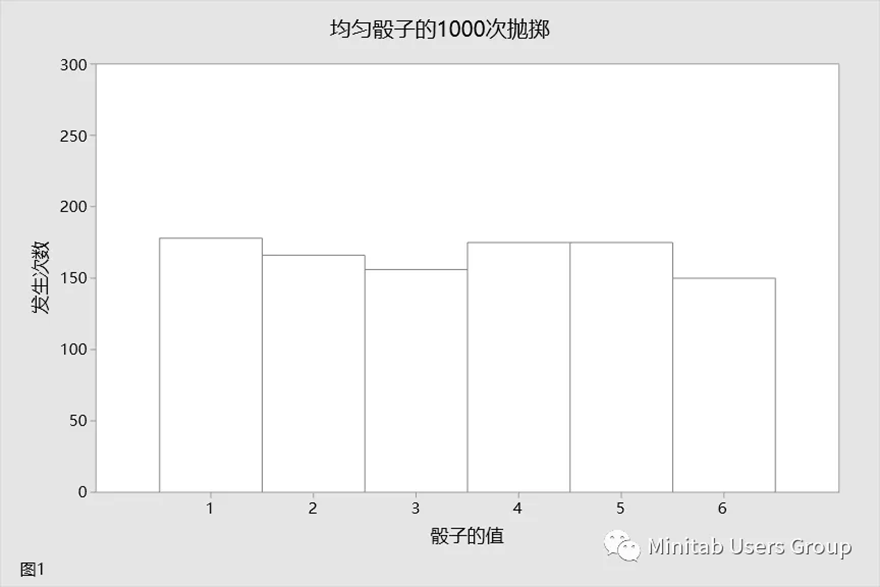
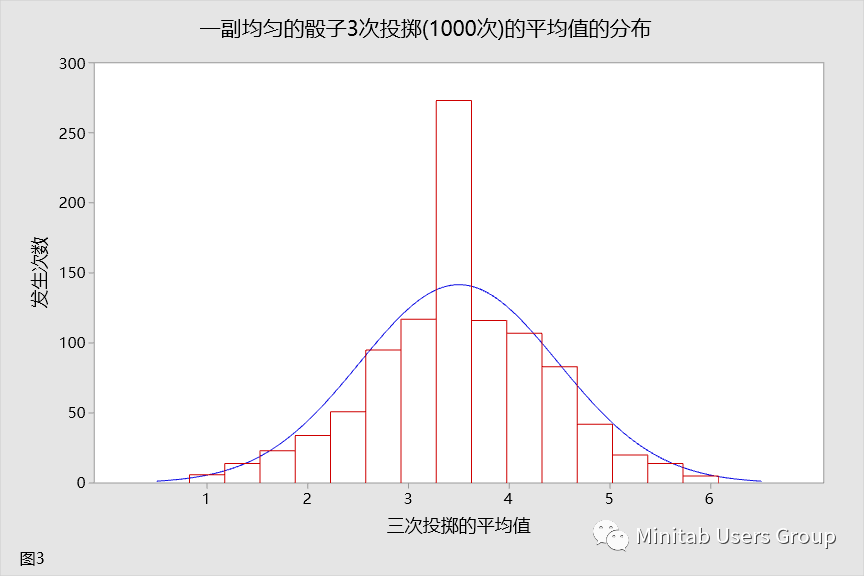
假设您掷骰子 1000 次。您希望得到相等数目的 1、2 等。让我们查看 1000 次骰子的分布(图1)。
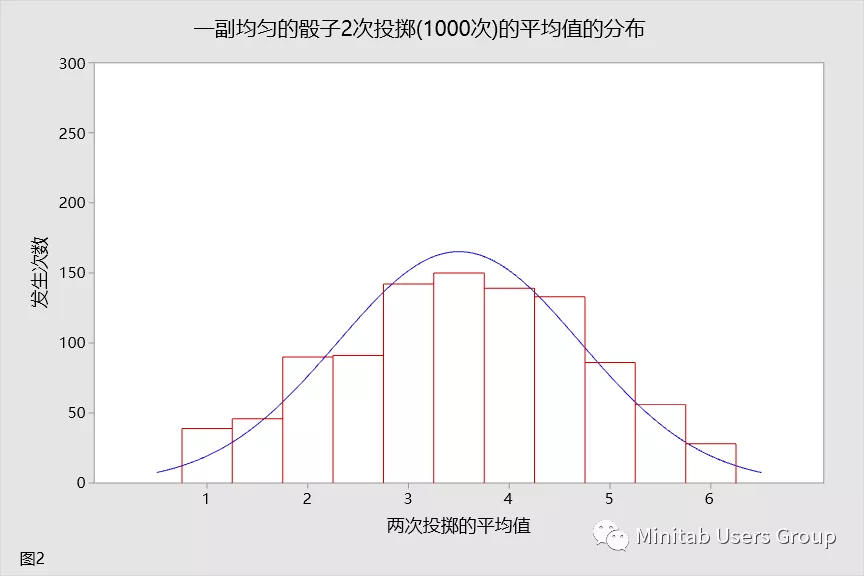
现在假设您将投掷 2 次,并采用两次投掷的平均值。您还将重复此试验 1000 次。让我们来看看两次投掷的平均值的分布。这种分布如图 2 所示。您是否注意到在只进行了两次投掷的情况下,平均值的分布已经呈现出了土堆形?
假设您现在投掷骰子三次,然后取三次投掷的平均值。再次重复此试验 1000 次。让我们来看看此举对投掷的平均值分布有何影响。这种分布如图 3 所示。同样,分布的形状与正态分布的形状相当接近。您是否注意到分布上发生了其他变化?
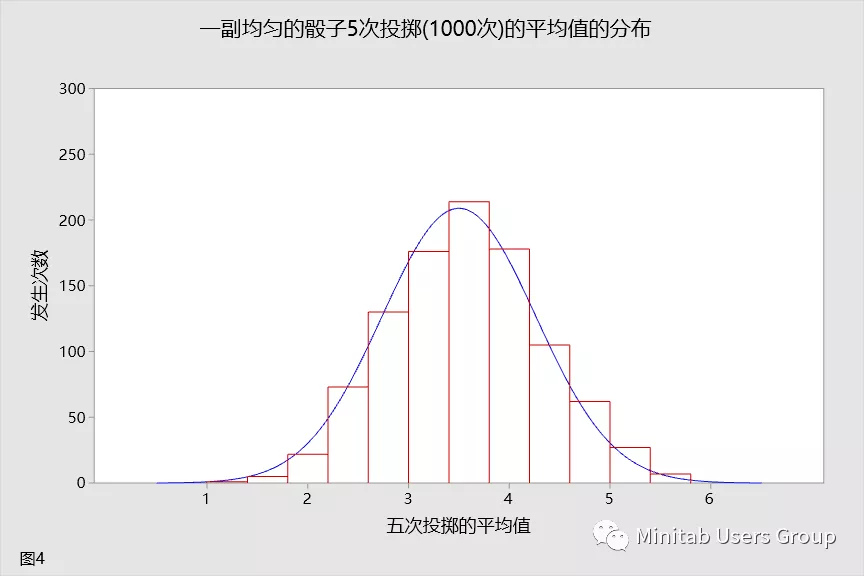
让我们投掷骰子五次,并取其平均值。再次重复此试验 1000 次。这种分布如图 4 所示。您是否已开始注意到所发生的情形中存在任何模式?
让我们继续增加平均投掷次数。此时您将投掷 10 次,并采用 10 次投掷的平均值。这种分布如图 5 所示。
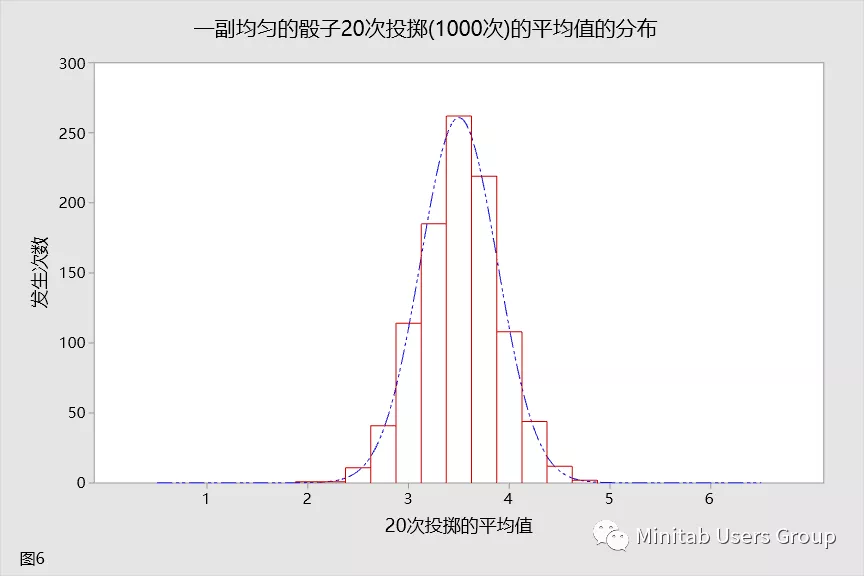
现在,随着您增加投掷次数,将看到两个现象。首先,您会看到,平均分布的形状开始与正态分布的形状相似。其次,您会看到,随着投掷次数的增加,分布变得越来越窄。让我们继续增加投掷次数。此时,您将投掷骰子 20 次。这种分布如图 6 所示。
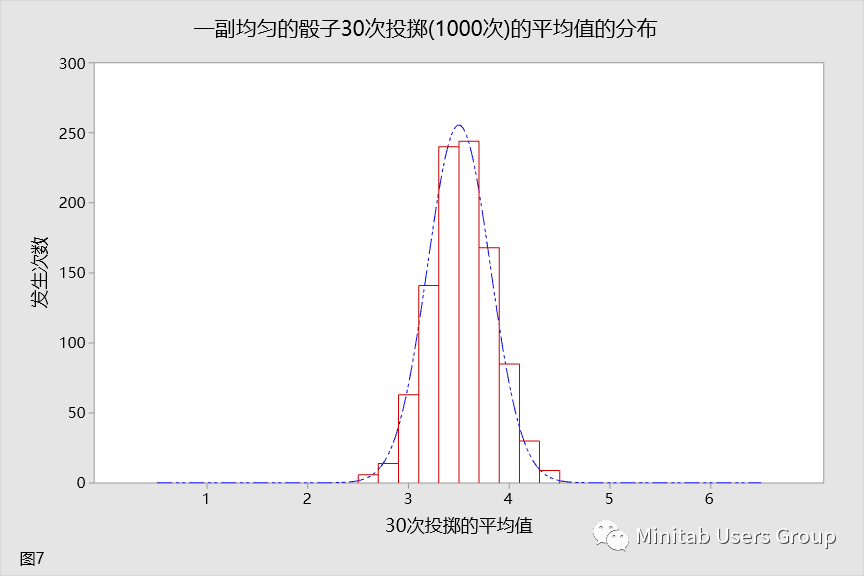
到现在,您应该确信增大样本数量对样本平均值分布是有影响的。您将再次增大样本数量,以强化这种认知。此时,您将投掷骰子 30 次。这种分布如图 7 所示。
让我们看看所呈现的情况,在一个图中绘制大小为 2、5、10、20、30 的样本的直方图,以查看变化的分布。
从上面的模拟结果,可以知道,当样本量大于30的时候,那么样本均值(取了1000次样本,得到1000个均值)的分布基本呈正态分布。
另外该定理还指出,如果根据总体不断重复绘制随机样本数量 n 以及有限均值 mu(y) 和标准差 sigma(y),然后在 n 较大时,样本均值的分布将近似呈正态分布,并且均值等于 mu(y),标准差等于 (sigma(y))/sqrt(n)。 收起阅读 »
但有些朋友,并不觉得这是一个错误的问题,甚至在他们的学习中还流传着这么一个说法:样本量大于30就可以认为是服从正态分布。当你向他问为什么的时候,会得到一个专业的解释——中心极限定理。
中心极限定理
中心极限定理(Central Limit Theorem)是统计学中最重要的结论之一。在这里,我并不想给出中心极限定理专业的定义,只需要了解它告诉我们:来自某总体的一个样本,无论该总体服从什么分布,只要样本容量足够大,其样本均值都近似服从正态分布。
请注意这里的说法:“样本均值“近似正态,而不是样本本身服从正态(不是说你抽了30个样品组成的样本数据就正态)。这里又有一个大家疑惑的地方,样本容量足够大,多大才是足够大?这个问题的答案和总体分布的形状相关,如果样本本是来自近似对称分布的总体,那么当样本量取相当小(如样本量取5)的值的时候,正态逼近的结果也会非常好。然后,如果总体的分布严重倾斜,则样本量必须取相当大的值。根据检验,对于大多数总体来说,样本容量取30或者更大,就足以得到令人满意的正态逼近结果。我想这可能就是错误认为样本量大于30就认为是正态分布的出处了。
模拟掷骰子展示中心极限定理
为了展示中心极限定理,模拟多次投掷骰子来说明。
假设您掷骰子 1000 次。您希望得到相等数目的 1、2 等。让我们查看 1000 次骰子的分布(图1)。
现在假设您将投掷 2 次,并采用两次投掷的平均值。您还将重复此试验 1000 次。让我们来看看两次投掷的平均值的分布。这种分布如图 2 所示。您是否注意到在只进行了两次投掷的情况下,平均值的分布已经呈现出了土堆形?
假设您现在投掷骰子三次,然后取三次投掷的平均值。再次重复此试验 1000 次。让我们来看看此举对投掷的平均值分布有何影响。这种分布如图 3 所示。同样,分布的形状与正态分布的形状相当接近。您是否注意到分布上发生了其他变化?
让我们投掷骰子五次,并取其平均值。再次重复此试验 1000 次。这种分布如图 4 所示。您是否已开始注意到所发生的情形中存在任何模式?
让我们继续增加平均投掷次数。此时您将投掷 10 次,并采用 10 次投掷的平均值。这种分布如图 5 所示。
现在,随着您增加投掷次数,将看到两个现象。首先,您会看到,平均分布的形状开始与正态分布的形状相似。其次,您会看到,随着投掷次数的增加,分布变得越来越窄。让我们继续增加投掷次数。此时,您将投掷骰子 20 次。这种分布如图 6 所示。
到现在,您应该确信增大样本数量对样本平均值分布是有影响的。您将再次增大样本数量,以强化这种认知。此时,您将投掷骰子 30 次。这种分布如图 7 所示。
让我们看看所呈现的情况,在一个图中绘制大小为 2、5、10、20、30 的样本的直方图,以查看变化的分布。
从上面的模拟结果,可以知道,当样本量大于30的时候,那么样本均值(取了1000次样本,得到1000个均值)的分布基本呈正态分布。
另外该定理还指出,如果根据总体不断重复绘制随机样本数量 n 以及有限均值 mu(y) 和标准差 sigma(y),然后在 n 较大时,样本均值的分布将近似呈正态分布,并且均值等于 mu(y),标准差等于 (sigma(y))/sqrt(n)。 收起阅读 »
十个常用的六西格玛统计工具及应用场景
六西格玛是一种质量改进方法,企业已经使用了几十年 - 因为它取得了成果。六西格玛项目遵循明确定义的一系列步骤,世界各国的每个行业的公司都使用这种方法来解决问题。
但是,六西格玛在很大程度上依赖于统计和数据分析,许多对质量改进不熟悉的人感到受到统计方面的威胁。你不必被吓倒。虽然数据分析确实对提高质量至关重要,但六西格玛的大多数分析并不难理解,即使您对统计数据不是很了解。但使用Minitab熟悉这些工具是一个很好的起点。本文简要介绍六西格玛中常用的10种统计工具,了解它们的作用以及它们为何如此重要。
1.帕累托图(Pareto图)
帕累托图来源于一种称为帕累托原则的观点,该观点认为大约80%的结果来自20%的原因。即使在我们的个人生活中,也很容易想到例子。例如,80%的时间你会穿买的衣服中20%的衣服,或者你在图书馆80%的时间只会听网易云音乐中收集的20%的音乐。
帕累托图可帮助您直观地了解此原则如何应用于您收集的数据。它是一种特殊类型的条形图,旨在将“少数几个”原因与“琐碎的”原因区分开来,使您能够专注于最重要的问题。例如,如果每次出现缺陷类型时就收集有关缺陷类型的数据,则帕累托图会显示哪些类型最常见,因此您可以集中精力解决最紧迫的问题。
2.直方图
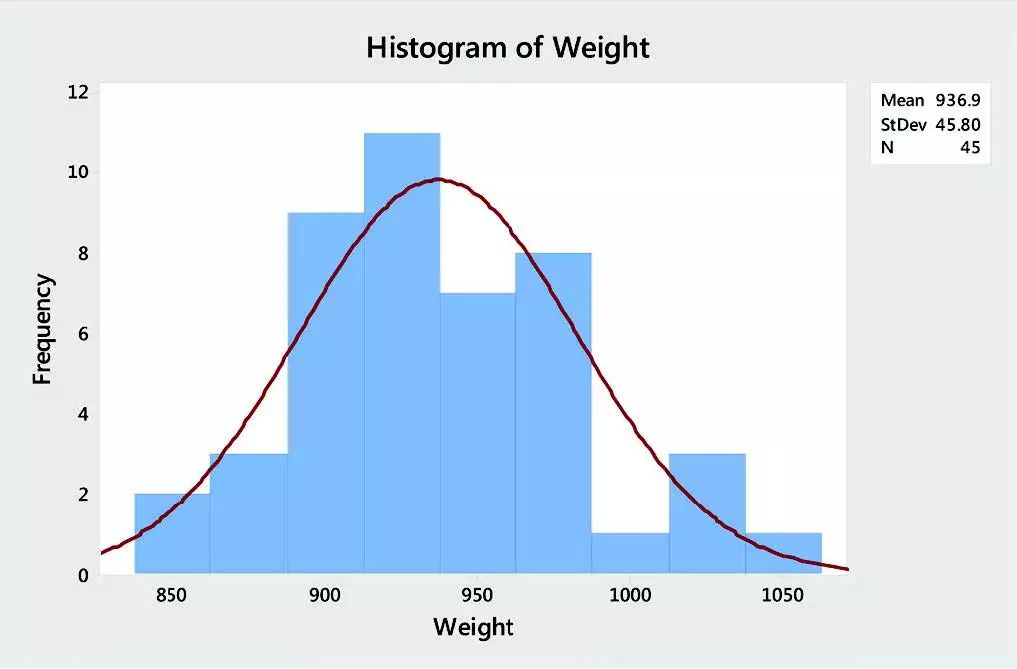
直方图是连续数据的图形快照。直方图使您能够快速识别数据的中心和范围。它显示了大部分数据落在哪里,以及最小值和最大值。直方图还显示您的数据是否为钟形,可以帮助您找到可能需要进一步调查的异常数据点。
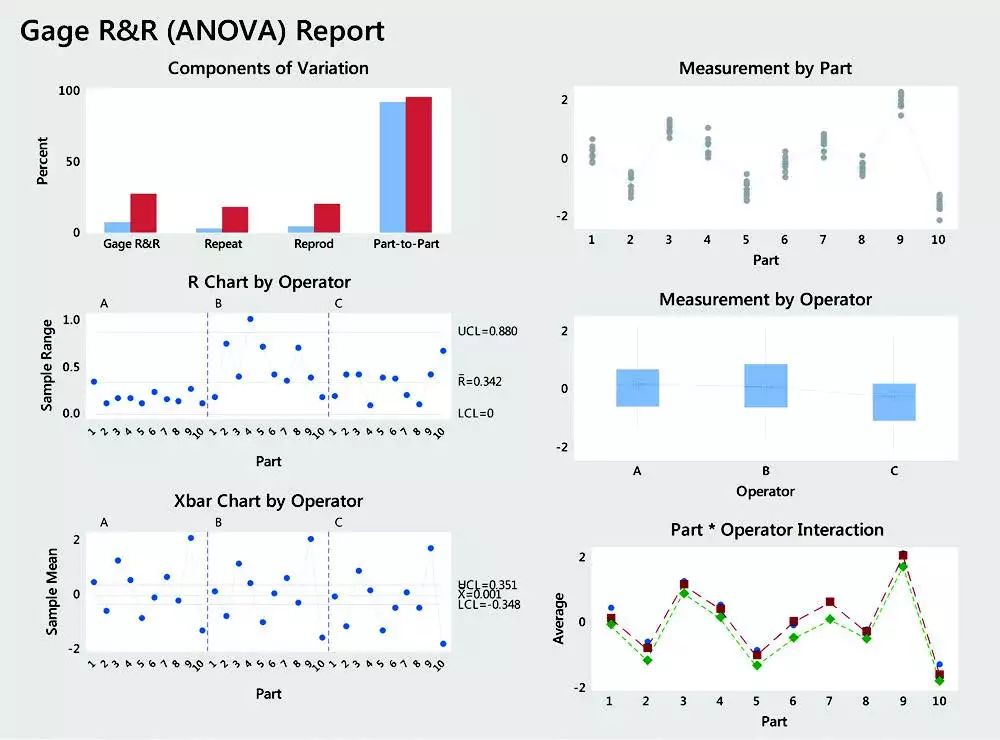
3.Gage R&R
准确的测量至关重要。你想用自己认为不可靠的数据来衡量自己吗?你会继续使用从未显示正确温度的温度计吗?如果您无法准确测量过程,则无法对其进行改进,这时Gage R&R就有了用武之地。此工具可帮助您确定连续型数值测量(如重量,直径和压力),当同一个人反复测量同一部件时,以及当不同的操作者测量相同部件时是否准确和精确。
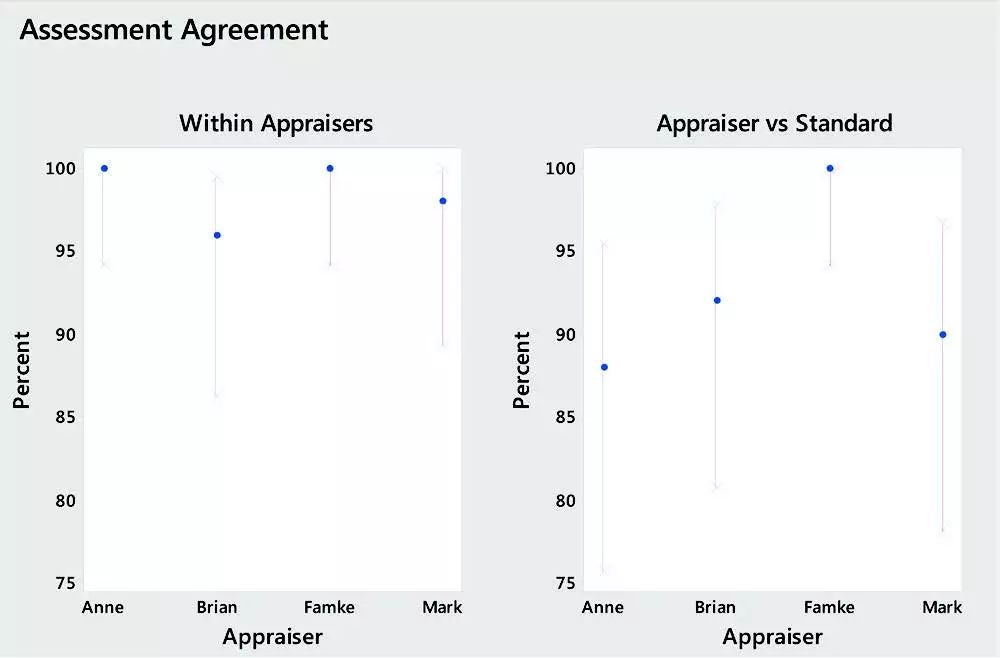
4.属性一致性分析
另一个确保您可以信任您的数据的工具是属性一致性分析。Gage R&R评估连续型数据的重复性和再现性,而属性一致性分析评估的是属性数据,例如通过或失败。此工具显示对这些类别进行评级的人是否与已知标准,与其他评估者以及他们自己一致。
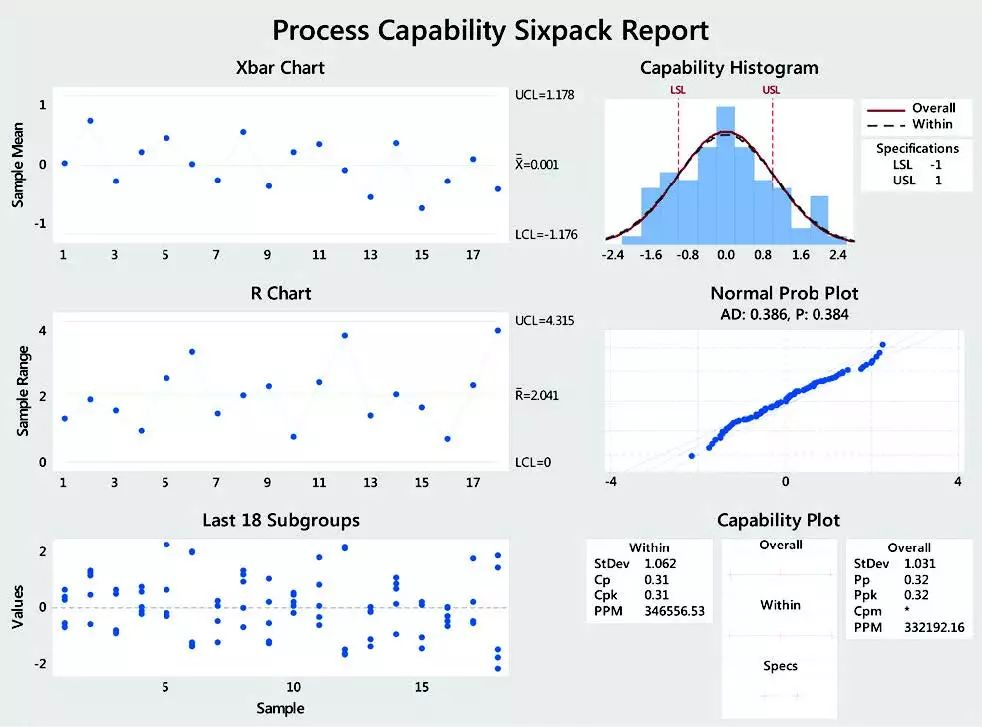
5.过程能力分析
几乎每个过程都具有可接受的下限和/或上限。例如,供应商的零件不能太大或太小,等待时间不能超过可接受的阈值,填充重量需要超过规定的最小值。能力分析向您展示您的流程与规范的完美程度,并深入了解如何改善不良流程。经常引用的能力指标包括Cpk,Ppk,Cp,Pp,百万机会缺陷数(DPMO)和西格玛水平(Z值)。
6.t检验
我们使用t检验来比较样本的平均值与目标值或另一个样本的平均值。例如,工艺参数调整后,想确定钢筋抗拉强度均值是否比原来的2000要高。如果您从两家供应商处购买调味糖浆,并想确定各自出货量的平均量是否有差异,您可以使用双样本t检验来比较两家供应商。
7.方差分析
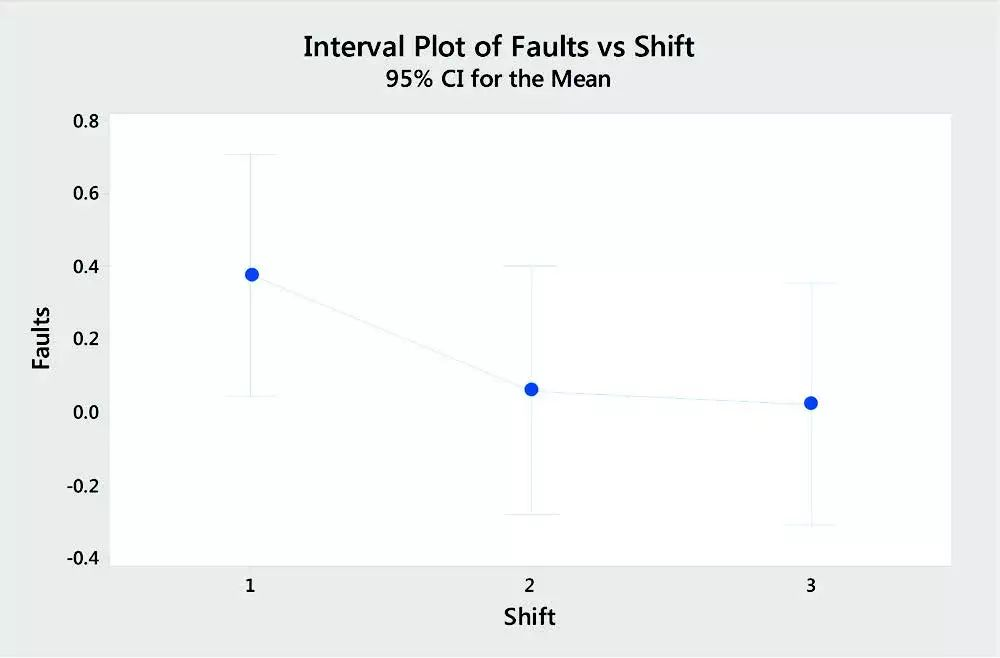
t检验将平均值与目标进行比较,或者将两个平均值相互比较,而ANOVA(方差分析的缩写)则可以比较两个以上总体的均值。例如,ANOVA可以显示3个班次的平均产量是否相等。您还可以使用ANOVA分析多于1个变量的均值。例如,您可以同时比较3班次的均值和2个制造地点的均值。
8.回归分析
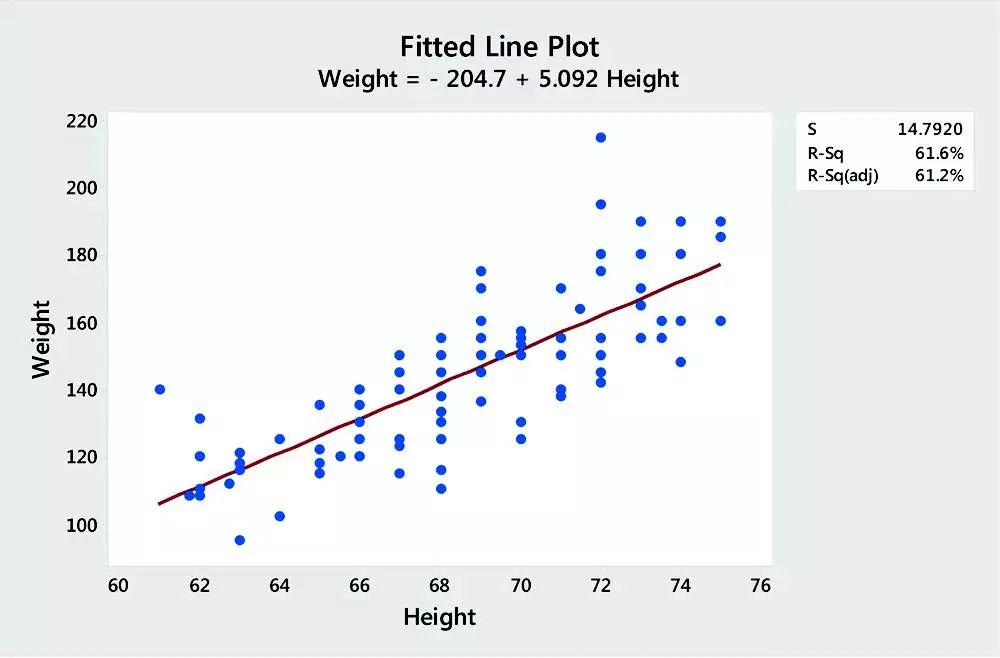
回归可帮助您确定输出与一个或多个输入因子之间是否存在关联。例如,您可以使用回归来检查公司的营销支出与其销售收入之间是否存在关联。当存在变量之间的关系时,您可以使用回归方程来描述该关系并预测给定输入值的未来输出值。
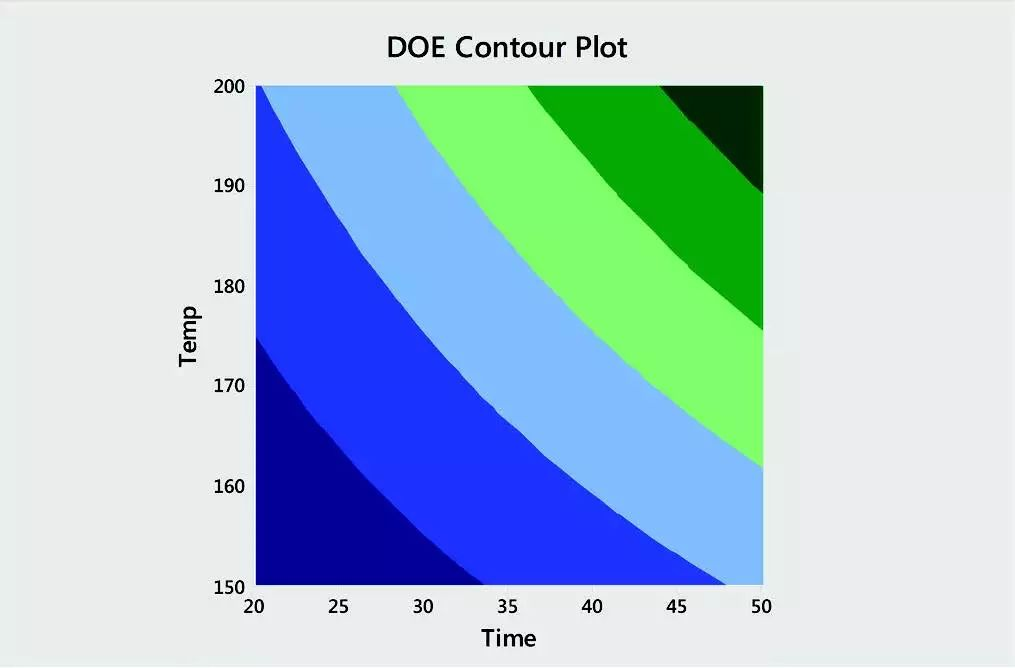
9.DOE(实验设计)
回归和ANOVA最常用于已经收集的数据。相比之下,实验设计(DOE)为您提供了一种有效的数据收集策略。它允许您同时更改或调整多个因子,以确定输入和输出之间是否存在关系。收集数据并识别重要输入后,您可以使用DOE确定每个因子的最佳设置。
10.控制图
每个过程都有一些自然的,固有的变化,但稳定(因此可预测)的过程是优质产品和服务的标志。重要的是要知道过程何时超出正常的自然变化,因为它可以指示需要解决的问题。控制图将“特殊原因”变化与可接受的自然变化区分开来。这些图表随时间变化绘制数据并标记失控数据点,因此您可以检测异常变化并在必要时采取措施。控制图还可以帮助您确保在未来持续改进流程。
小结
六西格玛可以为任何企业带来巨大的利益,但是获得这些收益需要收集和分析数据,以便您了解改进的机会并做出重大和可持续的变革。六西格玛项目的成功往往取决于在许多领域都是高技能专家的从业者,而不是统计数据。但是,通过对最常用的六西格玛统计数据和易于使用的统计软件(如Minitab)的基本了解,您可以处理与提高质量相关的统计任务,并自信地分析您的数据。 收起阅读 »
但是,六西格玛在很大程度上依赖于统计和数据分析,许多对质量改进不熟悉的人感到受到统计方面的威胁。你不必被吓倒。虽然数据分析确实对提高质量至关重要,但六西格玛的大多数分析并不难理解,即使您对统计数据不是很了解。但使用Minitab熟悉这些工具是一个很好的起点。本文简要介绍六西格玛中常用的10种统计工具,了解它们的作用以及它们为何如此重要。
1.帕累托图(Pareto图)
帕累托图来源于一种称为帕累托原则的观点,该观点认为大约80%的结果来自20%的原因。即使在我们的个人生活中,也很容易想到例子。例如,80%的时间你会穿买的衣服中20%的衣服,或者你在图书馆80%的时间只会听网易云音乐中收集的20%的音乐。
帕累托图可帮助您直观地了解此原则如何应用于您收集的数据。它是一种特殊类型的条形图,旨在将“少数几个”原因与“琐碎的”原因区分开来,使您能够专注于最重要的问题。例如,如果每次出现缺陷类型时就收集有关缺陷类型的数据,则帕累托图会显示哪些类型最常见,因此您可以集中精力解决最紧迫的问题。
2.直方图
直方图是连续数据的图形快照。直方图使您能够快速识别数据的中心和范围。它显示了大部分数据落在哪里,以及最小值和最大值。直方图还显示您的数据是否为钟形,可以帮助您找到可能需要进一步调查的异常数据点。
3.Gage R&R
准确的测量至关重要。你想用自己认为不可靠的数据来衡量自己吗?你会继续使用从未显示正确温度的温度计吗?如果您无法准确测量过程,则无法对其进行改进,这时Gage R&R就有了用武之地。此工具可帮助您确定连续型数值测量(如重量,直径和压力),当同一个人反复测量同一部件时,以及当不同的操作者测量相同部件时是否准确和精确。
4.属性一致性分析
另一个确保您可以信任您的数据的工具是属性一致性分析。Gage R&R评估连续型数据的重复性和再现性,而属性一致性分析评估的是属性数据,例如通过或失败。此工具显示对这些类别进行评级的人是否与已知标准,与其他评估者以及他们自己一致。
5.过程能力分析
几乎每个过程都具有可接受的下限和/或上限。例如,供应商的零件不能太大或太小,等待时间不能超过可接受的阈值,填充重量需要超过规定的最小值。能力分析向您展示您的流程与规范的完美程度,并深入了解如何改善不良流程。经常引用的能力指标包括Cpk,Ppk,Cp,Pp,百万机会缺陷数(DPMO)和西格玛水平(Z值)。
6.t检验
我们使用t检验来比较样本的平均值与目标值或另一个样本的平均值。例如,工艺参数调整后,想确定钢筋抗拉强度均值是否比原来的2000要高。如果您从两家供应商处购买调味糖浆,并想确定各自出货量的平均量是否有差异,您可以使用双样本t检验来比较两家供应商。
7.方差分析
t检验将平均值与目标进行比较,或者将两个平均值相互比较,而ANOVA(方差分析的缩写)则可以比较两个以上总体的均值。例如,ANOVA可以显示3个班次的平均产量是否相等。您还可以使用ANOVA分析多于1个变量的均值。例如,您可以同时比较3班次的均值和2个制造地点的均值。
8.回归分析
回归可帮助您确定输出与一个或多个输入因子之间是否存在关联。例如,您可以使用回归来检查公司的营销支出与其销售收入之间是否存在关联。当存在变量之间的关系时,您可以使用回归方程来描述该关系并预测给定输入值的未来输出值。
9.DOE(实验设计)
回归和ANOVA最常用于已经收集的数据。相比之下,实验设计(DOE)为您提供了一种有效的数据收集策略。它允许您同时更改或调整多个因子,以确定输入和输出之间是否存在关系。收集数据并识别重要输入后,您可以使用DOE确定每个因子的最佳设置。
10.控制图
每个过程都有一些自然的,固有的变化,但稳定(因此可预测)的过程是优质产品和服务的标志。重要的是要知道过程何时超出正常的自然变化,因为它可以指示需要解决的问题。控制图将“特殊原因”变化与可接受的自然变化区分开来。这些图表随时间变化绘制数据并标记失控数据点,因此您可以检测异常变化并在必要时采取措施。控制图还可以帮助您确保在未来持续改进流程。
小结
六西格玛可以为任何企业带来巨大的利益,但是获得这些收益需要收集和分析数据,以便您了解改进的机会并做出重大和可持续的变革。六西格玛项目的成功往往取决于在许多领域都是高技能专家的从业者,而不是统计数据。但是,通过对最常用的六西格玛统计数据和易于使用的统计软件(如Minitab)的基本了解,您可以处理与提高质量相关的统计任务,并自信地分析您的数据。 收起阅读 »
探索未知.预测未来------利用机器学习(CART)预测合格率
人类一直试图让机器具有智能,也就是人工智能(Artificial Intelligence)。从上世纪50年代,人工智能的发展经历了“推理期”,通过赋予机器逻辑推理能力使机器获得智能,当时的AI程序能够证明一些著名的数学定理,但由于机器缺乏知识,远不能实现真正的智能。因此,70年代,人工智能的发展进入“知识期”,即将人类的知识总结出来教给机器,使机器获得智能。 无论是“推理期”还是“知识期”,机器都是按照人类设定的规则和总结的知识运作,永远无法超越其创造者,其次人力成本太高。于是,一些学者就想到,如果机器能够自我学习问题不就迎刃而解了吗!机器学习(Machine Learning)方法应运而生,人工智能进入“机器学习时期”。机器学习的核心是“使用算法解析数据,从中学习,然后对世界上的某件事情做出决定或预测”。机器学习最大的突破是2006年的深度学习。深度学习是一类机器学习,目的是模仿人脑的思维过程,经常用于图像和语音识别。深度学习的出现导致了我们今天使用的(可能是理所当然的)许多技术。当你问你的iPhone关于今天的天气时,你的话语会用一种复杂的语音解析算法进行分析。如果没有深度学习,这一切都是不可能的。
机器学习与统计区别
机器学习是一类算法的总称,这些算法企图从大量历史数据中挖掘出其中隐含的规律,并用于预测或者分类,更具体的说,机器学习可以看作是寻找一个函数,输入是样本数据,输出是期望的结果,只是这个函数过于复杂,以至于不太方便形式化表达。
通常学习一个好的函数,分为以下三步:
1、选择一个合适的模型,这通常需要依据实际问题而定,针对不同的问题和任务需要选取恰当的模型。
2、判断一个函数的好坏,这需要确定一个衡量标准,如回归问题一般采用欧式距离,分类问题一般采用交叉验证函数。
3、找出“最好”的函数,如何从众多函数中最快的找出“最好”的那一个,学习得到“最好”的函数后,需要在新样本上进行测试,只有在新样本上表现很好,才算是一个“好”的函数。
机器学习的核心是“使用算法解析数据,从中学习,然后对世界上的某件事情做出决定或预测”。这意味着,与其显式地编写程序来执行某些任务,不如教计算机如何开发一个算法来完成任务。有三种主要类型的机器学习:监督学习、非监督学习和强化学习。
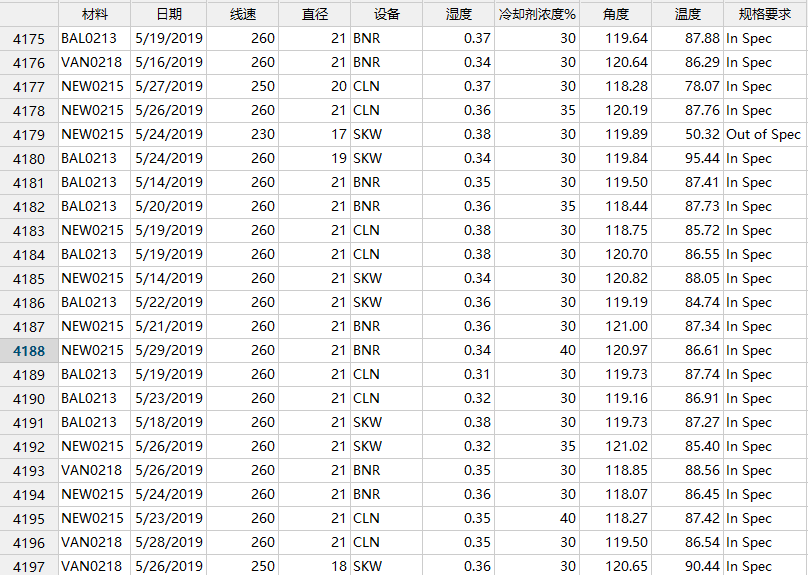
【案例分享】为了预测过程输出性能,提高客户满意度及产品质量,现从数据库中批量导入了2019年5月份生产报表,检测产品能否满足规格要求及相关生产环境,试分析影响产品质量的相关原因及预测结果。
本例共有9个变量,近5000个测试数据,其数据表如下:
在Minitab最新发布的版本Minitab19.2020中,除了可以将Python的脚本可以导入Minitab加载分析之外,还增加了机器学习的CART分析法。我们将上述案例用CART分析步骤如下:
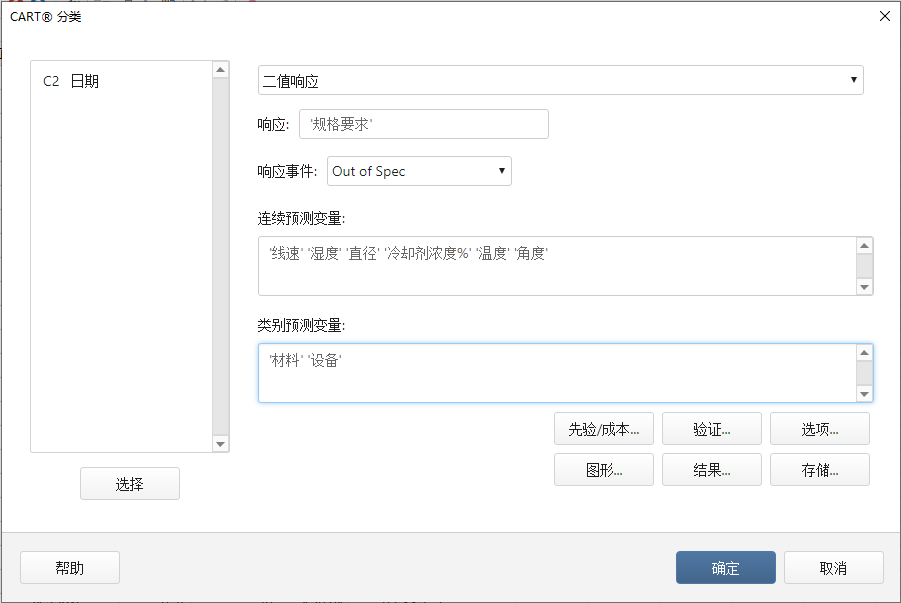
1、统计---预测分析---CART分类,将响应和影响因子分别填入对应位置
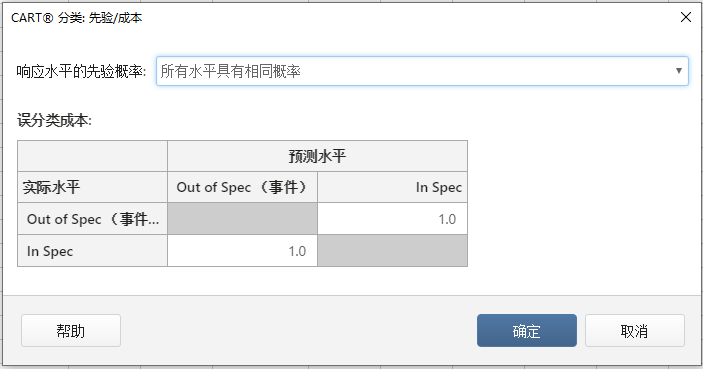
2、点击 先验/成本,设置误分类成本
误分类成本就是判断错误的风险,例如,在医学影像检测中,把健康的人误诊为病人还不是最糟的情况,只要医生能对诊断结果进行复查,并把健康的这个人找出来就可以了。但反过来,未能诊断出真正的病人而不提供给他任何治疗,则就非常危险了。默认情况下,Minitab 使用相等的成本 1。
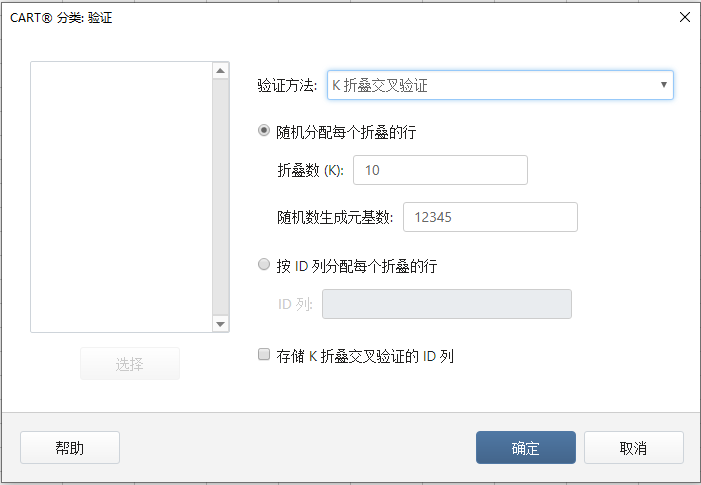
3、点击 验证,选择验证方法
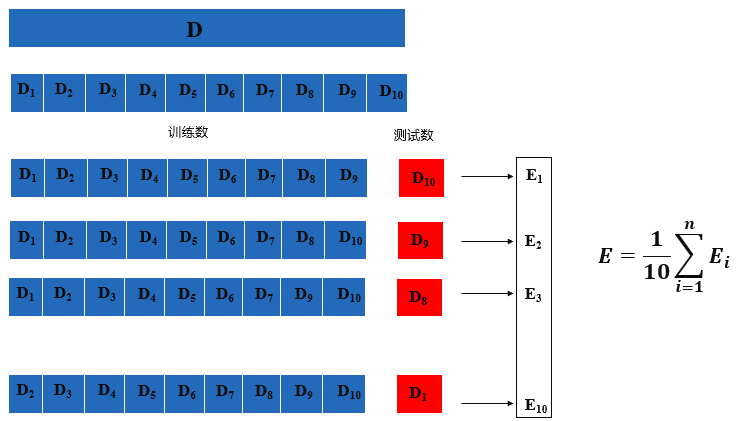
设置模型验证:数据通常被分为训练数据和测试数据
训练数据(学习数据)通常被用来创建模型及评估模型的系数;测试数据通常检模型性能,通过测试数据得到拟合值,在用训练数据的数据和对应的拟合值进行比较来检验模型的预测性能通过验证,防止模型过度拟合若用同一组数据来拟合模型并评估模型的拟合优度,会导致过度拟合,过度拟合的模型并不能用于很好的预测…..
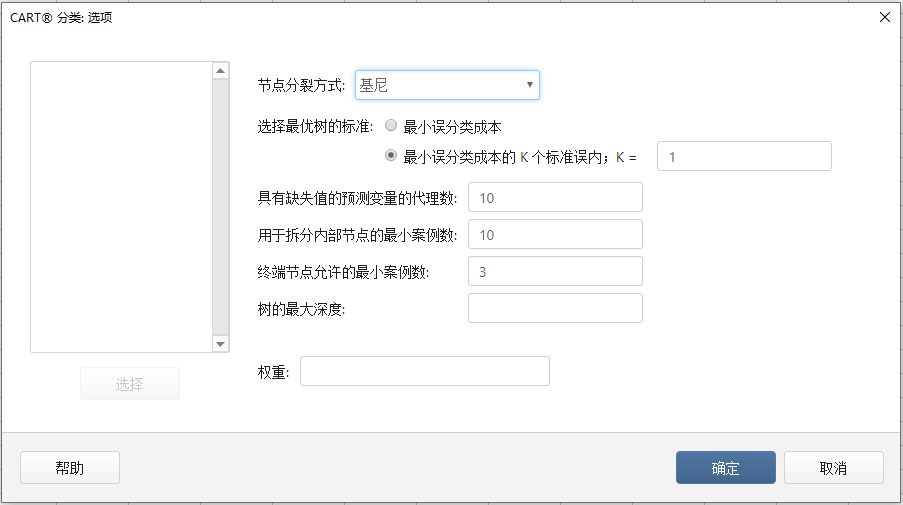
4、点击 选项,设置节点分裂方式
默认的节点分裂,选择 基尼
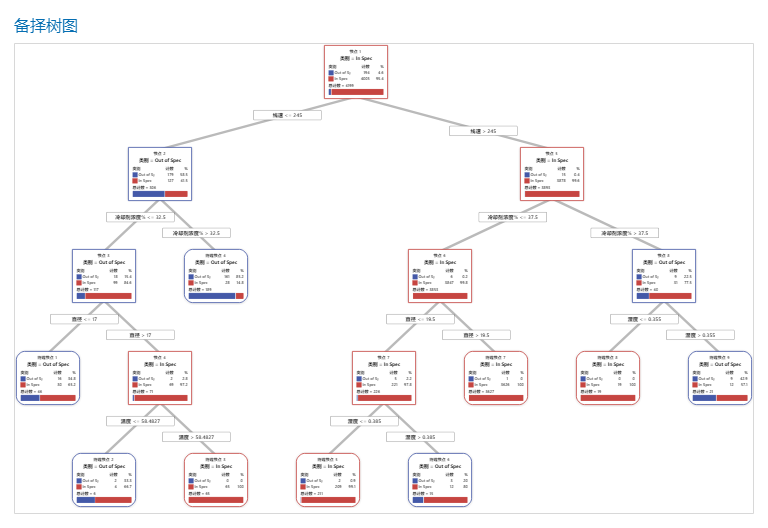
对所有对话框点击 确定,查看Minitab输出(部分):
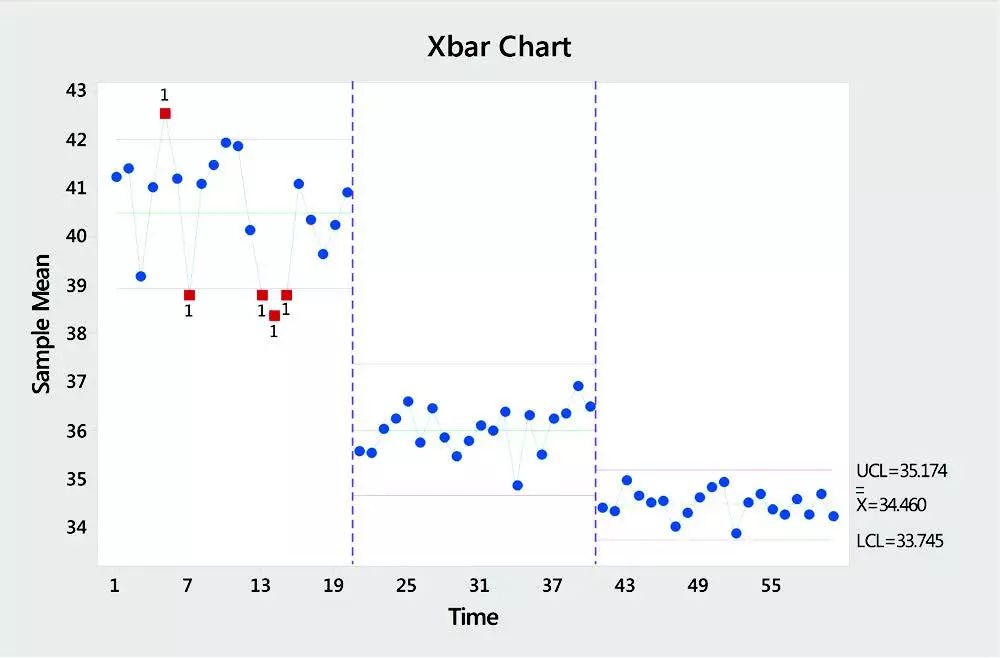
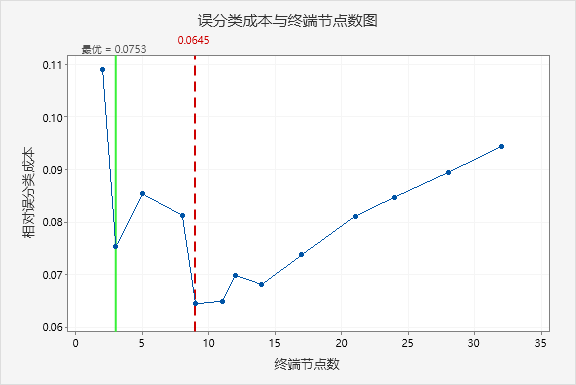
默认情况下,Minitab 为误分类成本在最小误分类成本 1 个标准误内的最小树生成输出。也可以识别最优树的序列中探索其他树。终端节点数越多,模型就越复杂。
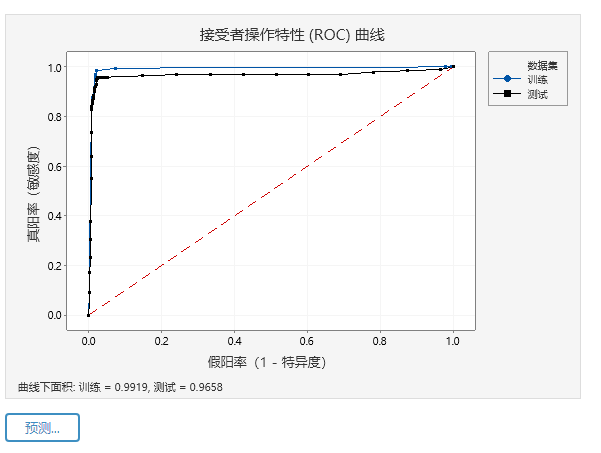
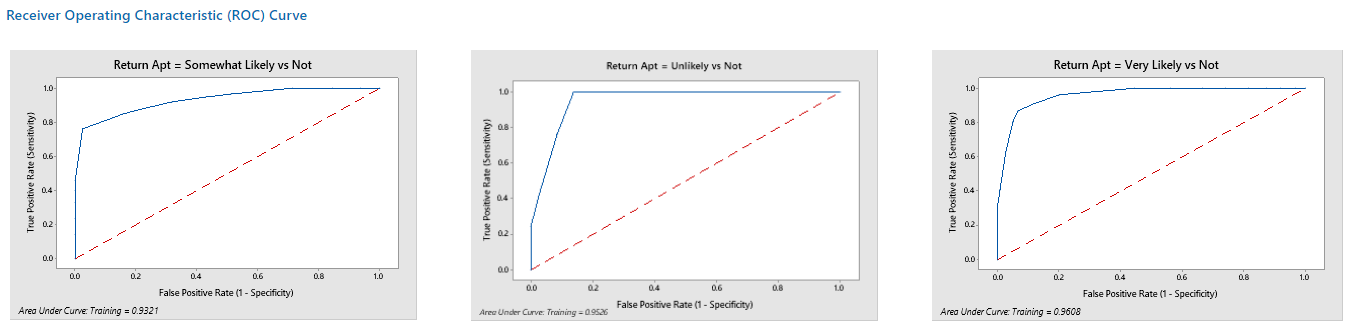
ROC曲线指受试者工作特征曲线 / 接收器操作特性曲线(receiver operating characteristic curve), 是反映敏感性和特异性连续变量的综合指标,是用构图法揭示敏感性和特异性的相互关系,它通过将连续变量设定出多个不同的临界值,从而计算出一系列敏感性和特异性,再以敏感性为纵坐标、(1-特异性)为横坐标绘制成曲线,曲线下面积越大,诊断准确性越高。
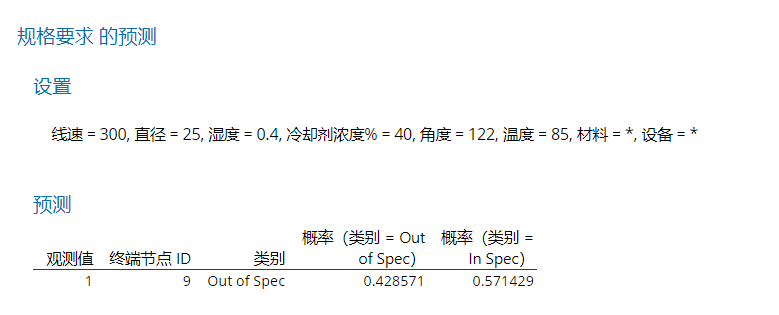
点击ROC图左下角的预测,可以根据模型预测不同场景下的输出概率。
总结:
机器学习是目前业界最为火热的一项技术,从网上的每一次淘宝的购买东西,到自动驾驶汽车技术,以及网络攻击抵御系统等等,都有机器学习的因子在内,同时机器学习也是最有可能使人类完成“AI 梦”的一项技术,各种人工智能目前的应用,如微软小冰聊天机器人,到计算机视觉技术的进步,都有机器学习努力的成分。作为全球领先的统计分析软件,Minitab在2018年收购了SPM,并在Minitab.19.2020版中增加了预测分析的CART分类和CART回归功能,能够帮助我们了解一些机器学习的相关知识与概念,更好的理解为我们带来莫大便利技术的背后原理,以及让我们更好的理解当代科技的进程。 收起阅读 »
田口设计案例-晶体外延层生长实验
案例背景
生产集成电路(IC)器件的一个初始步骤是在抛光的硅晶片上产生一个外延层,镶在一个称为感应器的六面柱体上(每面有两块晶片),这个六面柱体在一个钟形容器里旋转,这个容器通过其顶部的喷咀喷入化学蒸汽并加热。这个过程持续到外延层生长到所要求的厚度,厚度的目标值14.5微米(um),其误差范围为14.5土0.5微米,即实际的厚度应该尽可能接近14.5,并在区间[14,15]内。当前的设置造成的偏差超过了指定的1.0微米,于是试验人员需要找出可以设置的过程因子使得外延层的不均匀性达到最小,同时确保平均厚度尽可能接近目标值。
稳健参数设计
响应变差可以通过减小噪声变差来减小,但这可能要付出高的经济代价。由Genichi Taguchi最先提出的稳健参数设计(robust parameter design)是一种可选择的策略,该策略是通过探索控制因子与噪声因子间的交互效应来改变控制因子的水平组合来减小响应变差。因为控制因子通常很易于改变,所以稳健参数设计比直接减小噪声变差更经济更方便。
外延层生长试验的因子和水平
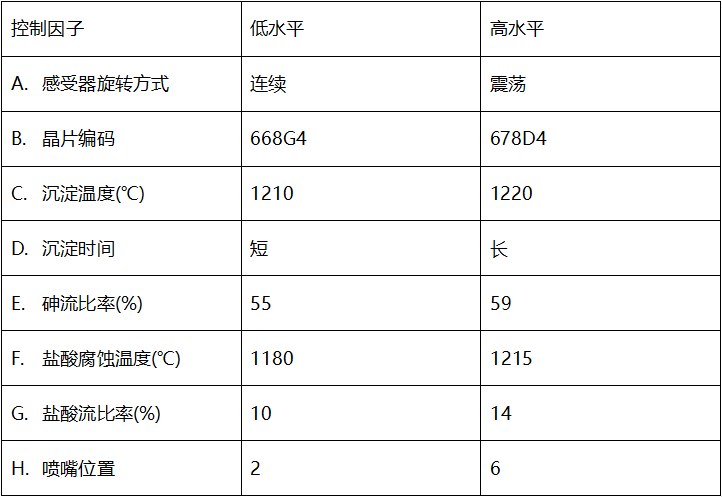
原始外延层生长试验的试验因子如下表所示,共有八个控制因子(A-H)和两个噪声因子(L和M)。
每个感受器有四个面,因此因子M有四水平。在每一个面上位置幽分顶部和底部(因子L)。在最初的试验中, Kackar and Shoemaber (1986)报告六个面的结果.为了方便说明,这里我们只考虑四个面。因为所期望的是在任何面和位置上都有均匀的厚度,所以因子L和M都处理为噪声因子。
厚度的目标值是14.5微米,规定误差限制在14.5士0.5微米。这样,试验的目标就是在保持14.5微米的平均厚度的同时,最小化外延层在四个面以及顶、底部上厚度的不均匀性。
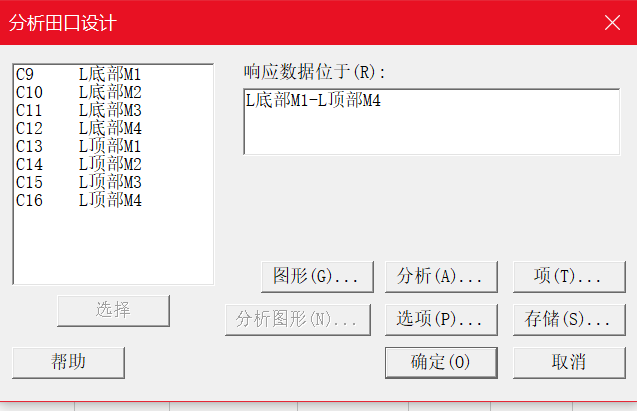
乘积表分析
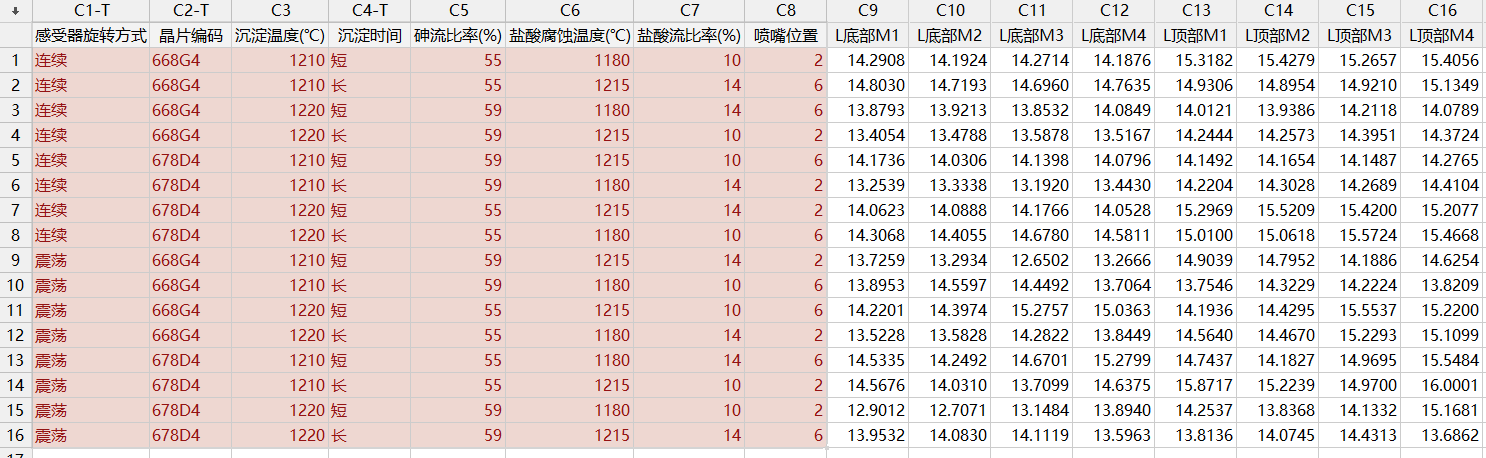
此田口设计的内表采用L16 (2^8)的正交表(表示设计有16个实验和8个因子,以及 每个因子2个水平)。外表对两个噪声因子选用了2x4设计,这样每个控制因子水平组合就有8个观测值。那么,按照乘积表分析的话就有16x8=128次实验。
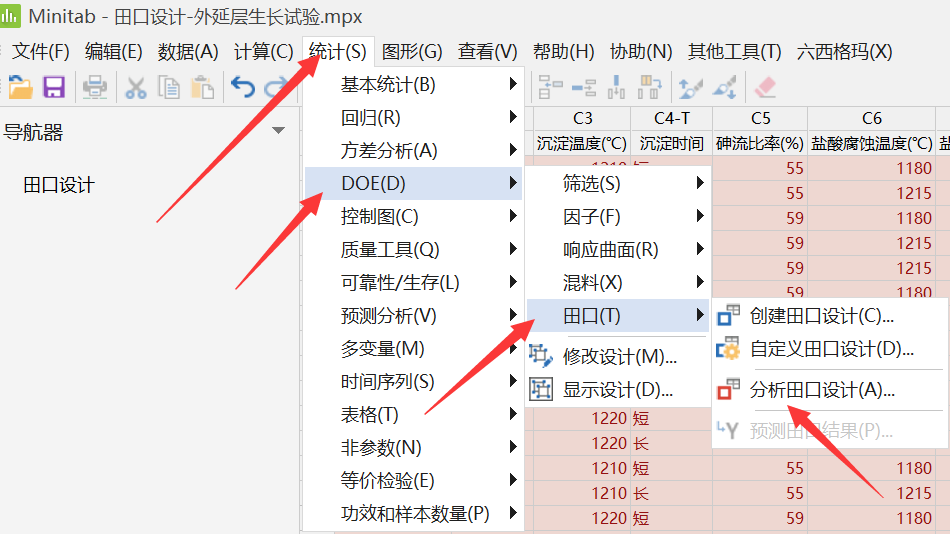
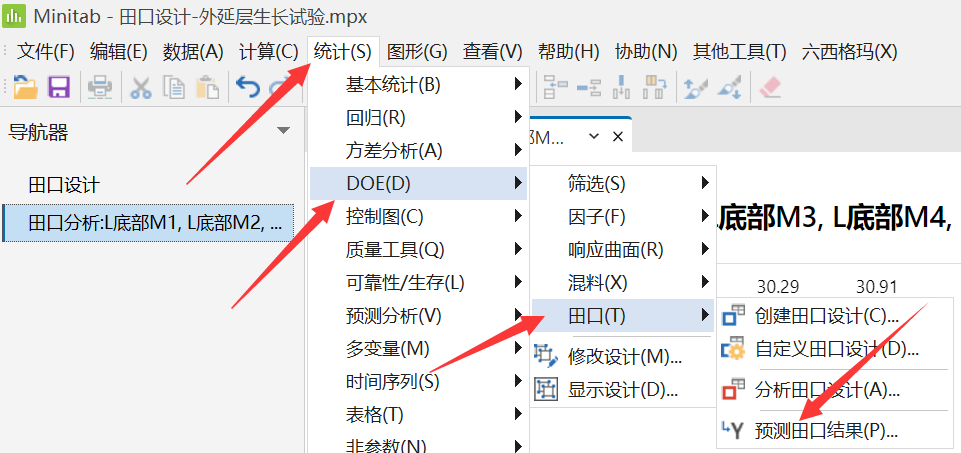
Minitab中田口分析
望目特征问题的两步程序:
选择散度因子的水平使散度最小化(信噪比最大化)
选择调节因子的水平使位置达到目标值
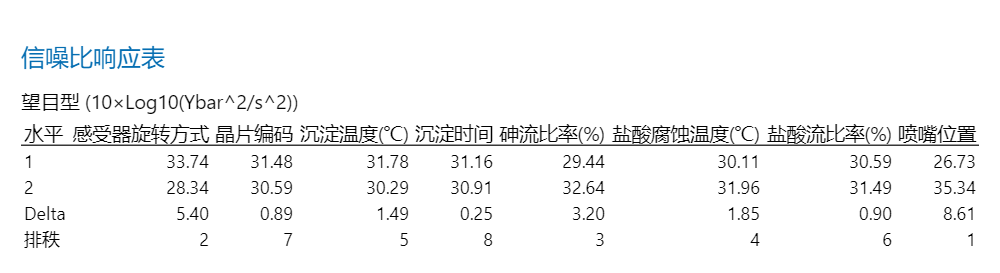
要想第一步中信噪比最大化,则应该取因子组合为:
A1B1C1D1E2F2G2H2
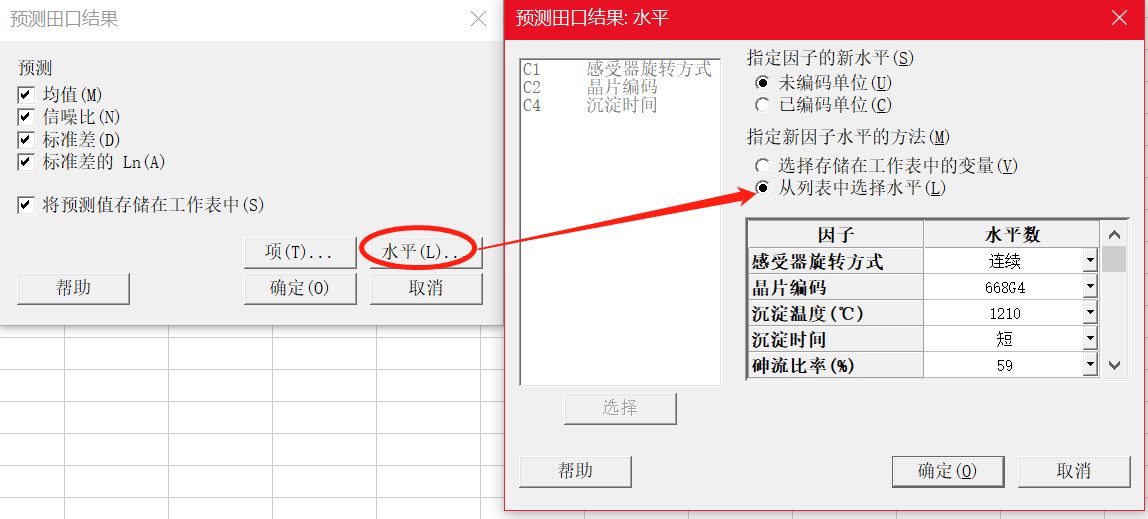
基于以上最佳信噪比组合,预测均值是否达到目标值14.5微米。
由以上预测结果可知,均值没有达到14.5微米,需要进行调节。
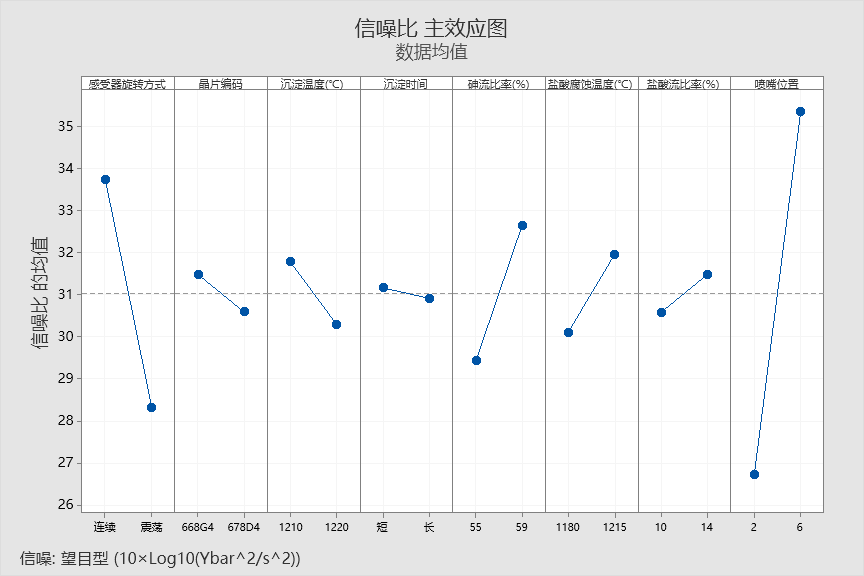
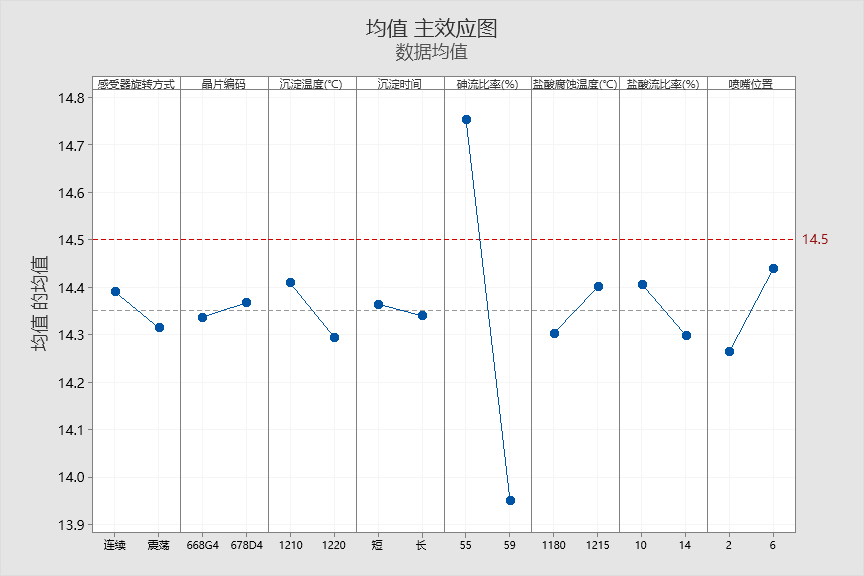
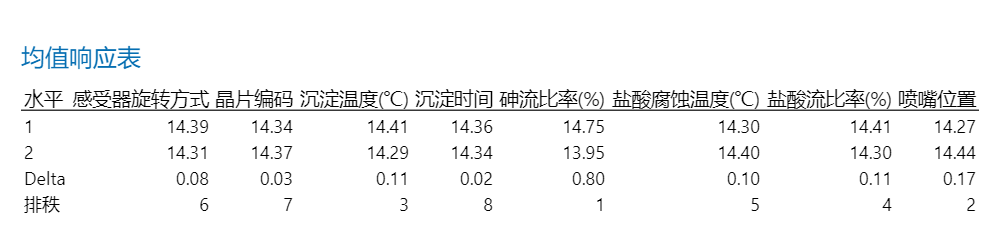
从下面的均值主效应图中可以发现,砷流比率(%)是一个合适的调节因子。
为此,我们固定A1B1C1D1F2G2H2,改变E的水平进行预测,结果如下:
根据预测的结果,我们下一步将会固定A1B1C1D1F2G2H2,因子E砷流比率(%)在(55,59)范围内选取,再次进行新的实验。
思考
在本案例中为了实现稳健参数设计,我们用的是田口设计中的乘积表,但乘积表实验次数太多了(128次),有没有其他方法也可以实现稳健参数设计呢?另外,乘积表分析除了实验次数多以外,还有没有其他一些缺点呢? 收起阅读 »
生产集成电路(IC)器件的一个初始步骤是在抛光的硅晶片上产生一个外延层,镶在一个称为感应器的六面柱体上(每面有两块晶片),这个六面柱体在一个钟形容器里旋转,这个容器通过其顶部的喷咀喷入化学蒸汽并加热。这个过程持续到外延层生长到所要求的厚度,厚度的目标值14.5微米(um),其误差范围为14.5土0.5微米,即实际的厚度应该尽可能接近14.5,并在区间[14,15]内。当前的设置造成的偏差超过了指定的1.0微米,于是试验人员需要找出可以设置的过程因子使得外延层的不均匀性达到最小,同时确保平均厚度尽可能接近目标值。
稳健参数设计
响应变差可以通过减小噪声变差来减小,但这可能要付出高的经济代价。由Genichi Taguchi最先提出的稳健参数设计(robust parameter design)是一种可选择的策略,该策略是通过探索控制因子与噪声因子间的交互效应来改变控制因子的水平组合来减小响应变差。因为控制因子通常很易于改变,所以稳健参数设计比直接减小噪声变差更经济更方便。
外延层生长试验的因子和水平
原始外延层生长试验的试验因子如下表所示,共有八个控制因子(A-H)和两个噪声因子(L和M)。
每个感受器有四个面,因此因子M有四水平。在每一个面上位置幽分顶部和底部(因子L)。在最初的试验中, Kackar and Shoemaber (1986)报告六个面的结果.为了方便说明,这里我们只考虑四个面。因为所期望的是在任何面和位置上都有均匀的厚度,所以因子L和M都处理为噪声因子。
厚度的目标值是14.5微米,规定误差限制在14.5士0.5微米。这样,试验的目标就是在保持14.5微米的平均厚度的同时,最小化外延层在四个面以及顶、底部上厚度的不均匀性。
乘积表分析
此田口设计的内表采用L16 (2^8)的正交表(表示设计有16个实验和8个因子,以及 每个因子2个水平)。外表对两个噪声因子选用了2x4设计,这样每个控制因子水平组合就有8个观测值。那么,按照乘积表分析的话就有16x8=128次实验。
Minitab中田口分析
望目特征问题的两步程序:
选择散度因子的水平使散度最小化(信噪比最大化)
选择调节因子的水平使位置达到目标值
要想第一步中信噪比最大化,则应该取因子组合为:
A1B1C1D1E2F2G2H2
基于以上最佳信噪比组合,预测均值是否达到目标值14.5微米。
由以上预测结果可知,均值没有达到14.5微米,需要进行调节。
从下面的均值主效应图中可以发现,砷流比率(%)是一个合适的调节因子。
为此,我们固定A1B1C1D1F2G2H2,改变E的水平进行预测,结果如下:
根据预测的结果,我们下一步将会固定A1B1C1D1F2G2H2,因子E砷流比率(%)在(55,59)范围内选取,再次进行新的实验。
思考
在本案例中为了实现稳健参数设计,我们用的是田口设计中的乘积表,但乘积表实验次数太多了(128次),有没有其他方法也可以实现稳健参数设计呢?另外,乘积表分析除了实验次数多以外,还有没有其他一些缺点呢? 收起阅读 »
过程能力分析04—非正态(非参数方法)
通过此系列文章,目前我们学习了过程能力分析的意义,基于Minitab的正态/非正态数据过程能力分析的思路和方法,其中在非正态数据能力分析中,我们讲了两种方法——转换方法和拟合其他分布方法。文章发布后,果不其然大家又有了新的问题,我们今天先来回答一些问题,再来介绍非正态数据能力分析的另外一种方法——非参数方法。
你有这些疑问吗?
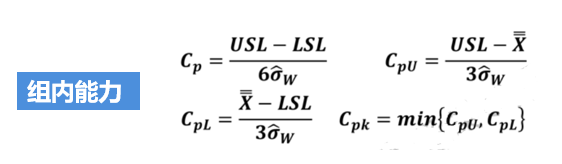
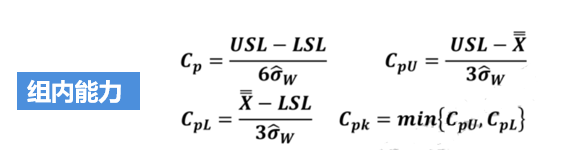
基于前面文章的说明,我们反复强调过程能力分析的一些前提条件(计算Cp/Cpk要求数据满足“独立、正态、MSA合格、稳定”,计算Pp/Ppk只要求数据满足“MSA合格,独立”)。我们还说过,以下公式只适用于正态分布数据。
那么,你有跟下面这位朋友一样的疑问吗?
对于这个问题,首先我们要知道,不管是正态数据还是非正态数据都可以计算Ppk,但是拟合分布不同计算结果肯定是有差异。如果数据正态可以按照上面的公式计算,如果非正态我们前面文章介绍了两种方法——转换/拟合其他分布。虽然计算Ppk不需要数据正态,但是做为数据分析人员我们要知道到底选择的正态方法还是非正态方法。直白点说,虽然计算Ppk不要求数据正态,但是我们仍然要在做过程能力分析计算Ppk之前执行正态性检验,只有这样你才知道从Minitab的哪个窗口进入分析。
另外一个问题,也是经常被问到(就我而言,就最少被问过不下20次)。
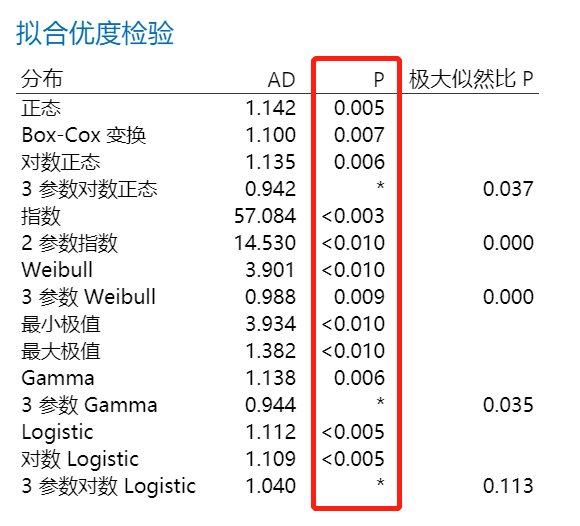
前面文章我们说过,如果数据非正态不要急着转换数据或盲目套其他分布,我们可以先来个“个体分布标识”。但是在“个体分布标识”中我们可能会遇到以下情况——两种变换都不行,14种分布中没有一个能够很好拟合数据。
对于这种情况,我们需要花费更多的精力回到数据搜集的现场做调查,而不是为了得到一个过程能力报告去寻求统计专家的帮助(再高明的专家如果不去现场也只能帮助你猜原因)。
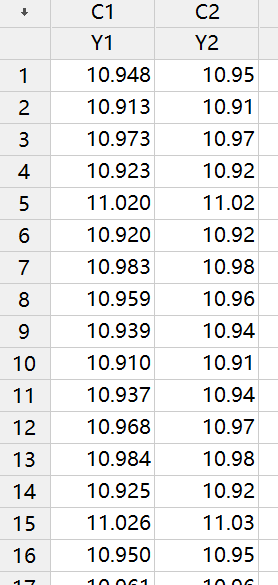
比如像上面的“个体分布标识”输出,为什么找不到合适分布,其实我把数据展示一部分给大家看一下就知道原因了(测量系统分辨力不够或数据经过了修约处理)。
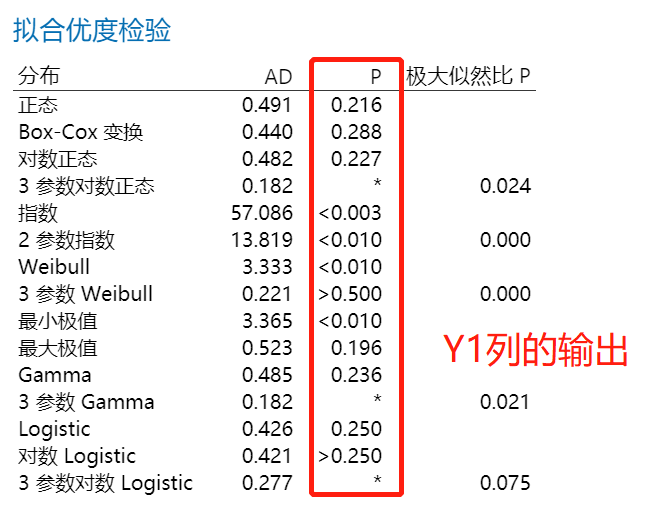
上面的“个体分布标识”是Y2的输出结果,如果我对Y1列执行相同分析呢?
这里我只是展示一种可能找不到合适分布的原因——测量系统分辨力不足,那你的数据又是什么原因导致找不到合格分布呢?这个问题别人无法回答,需要你去现场找答案。那如果我所有怀疑的原因都找了一圈结果还是没有发现问题出在哪里,那可不可以计算过程能力呢?这时候如果你的数据量比较大的话(最好1000以上),我们还有一种方法可以来计算过程能力——非参数方法。这种方法不需要知道拟合分布,但要求样本量比较大。
非参数方法
非参数方法计算过程能力的核心逻辑跟前面介绍的拟合其他分布是一样的。
因为找不到合适拟合分布,所以这里的分位数计算就不能用之前的方法了,在这里你可以手算也可以利用 Minitab自带的宏命令来计算这些分位数。
点击“帮助”菜单,我们可以在帮助文档中找到相应的宏命令。
把这个宏命令下载下来,运行之前请阅读仔细阅读帮助中说明,尤其要注意把宏放到指定的位置。 收起阅读 »
你有这些疑问吗?
基于前面文章的说明,我们反复强调过程能力分析的一些前提条件(计算Cp/Cpk要求数据满足“独立、正态、MSA合格、稳定”,计算Pp/Ppk只要求数据满足“MSA合格,独立”)。我们还说过,以下公式只适用于正态分布数据。
那么,你有跟下面这位朋友一样的疑问吗?
对于这个问题,首先我们要知道,不管是正态数据还是非正态数据都可以计算Ppk,但是拟合分布不同计算结果肯定是有差异。如果数据正态可以按照上面的公式计算,如果非正态我们前面文章介绍了两种方法——转换/拟合其他分布。虽然计算Ppk不需要数据正态,但是做为数据分析人员我们要知道到底选择的正态方法还是非正态方法。直白点说,虽然计算Ppk不要求数据正态,但是我们仍然要在做过程能力分析计算Ppk之前执行正态性检验,只有这样你才知道从Minitab的哪个窗口进入分析。
另外一个问题,也是经常被问到(就我而言,就最少被问过不下20次)。
前面文章我们说过,如果数据非正态不要急着转换数据或盲目套其他分布,我们可以先来个“个体分布标识”。但是在“个体分布标识”中我们可能会遇到以下情况——两种变换都不行,14种分布中没有一个能够很好拟合数据。
对于这种情况,我们需要花费更多的精力回到数据搜集的现场做调查,而不是为了得到一个过程能力报告去寻求统计专家的帮助(再高明的专家如果不去现场也只能帮助你猜原因)。
比如像上面的“个体分布标识”输出,为什么找不到合适分布,其实我把数据展示一部分给大家看一下就知道原因了(测量系统分辨力不够或数据经过了修约处理)。
上面的“个体分布标识”是Y2的输出结果,如果我对Y1列执行相同分析呢?
这里我只是展示一种可能找不到合适分布的原因——测量系统分辨力不足,那你的数据又是什么原因导致找不到合格分布呢?这个问题别人无法回答,需要你去现场找答案。那如果我所有怀疑的原因都找了一圈结果还是没有发现问题出在哪里,那可不可以计算过程能力呢?这时候如果你的数据量比较大的话(最好1000以上),我们还有一种方法可以来计算过程能力——非参数方法。这种方法不需要知道拟合分布,但要求样本量比较大。
非参数方法
非参数方法计算过程能力的核心逻辑跟前面介绍的拟合其他分布是一样的。
因为找不到合适拟合分布,所以这里的分位数计算就不能用之前的方法了,在这里你可以手算也可以利用 Minitab自带的宏命令来计算这些分位数。
点击“帮助”菜单,我们可以在帮助文档中找到相应的宏命令。
把这个宏命令下载下来,运行之前请阅读仔细阅读帮助中说明,尤其要注意把宏放到指定的位置。 收起阅读 »
过程能力分析03—非正态(拟合其他分布法)
对于过程能力分析,通过之前的文章我们知道在计算能力指标之前需要确认一些前提条件是否满足要求(独立,正态,MSA合格,稳定),今天我们继续延续之前的话题来讨论非正态数据如何做过程能力分析。
非正态解决方案
如果您使用为正态数据设计的能力分析,您的数据必须服从正态分布。
对于上面的这些公式,我相信很多朋友比较熟悉(不同教材在公式写法和叫法上可能稍微不同),但我们今天讨论的不是这组公式,为什么呢?因为上面这些公式只适用于正态数据,而我们今天想分享的是非正态数据的能力分析。
对于非正态数据,我们可以通过以下方法来获得准确描述生成非正态数据的过程的能力指数。
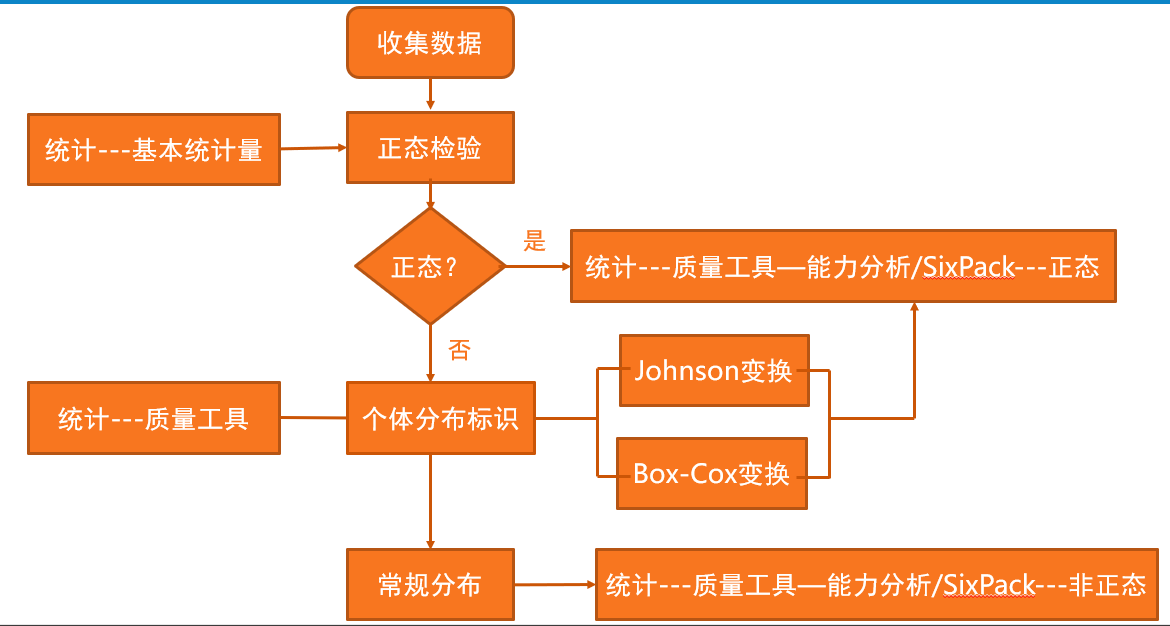
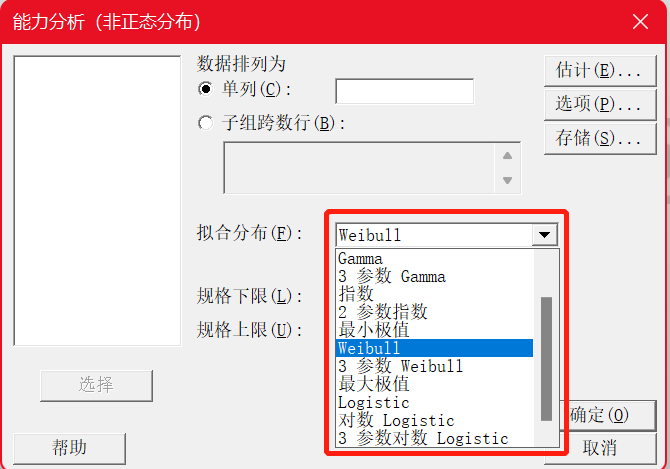
正如你所看到的,解决方法有很多,当然方法选择不同结果肯定是有差异的,那么问题又来了,哪个方法是比较合适的呢?别急,我们可以先参考以下路径图帮助我们选择。
在上一篇文章中我们分享了变换的方法(Box-Cox变换),在这篇文章中,我们打算找到拟合数据的合适分布(除了正态分布外,Minitab在这里还提供了其他13种分布),采用非正态的方法来计算Ppk(注意,由于是非正态分布,这时候就无法计算Cp/CpK了)。
拟合其他分布法(ISO方法)原理
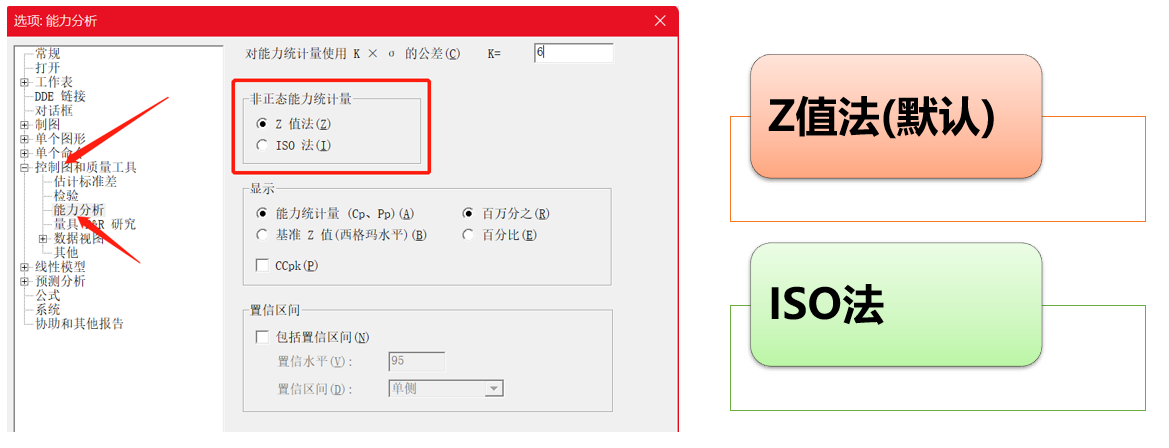
对于非正态数据,Minitab后台提供两种算法(21版本中,默认算法为“Z值法”)
但是,我们今天要分享的是“ISO方法”,原因很简单,这种算法大家在六西格玛相关课程和教材中其实学过了(先混个脸熟)。
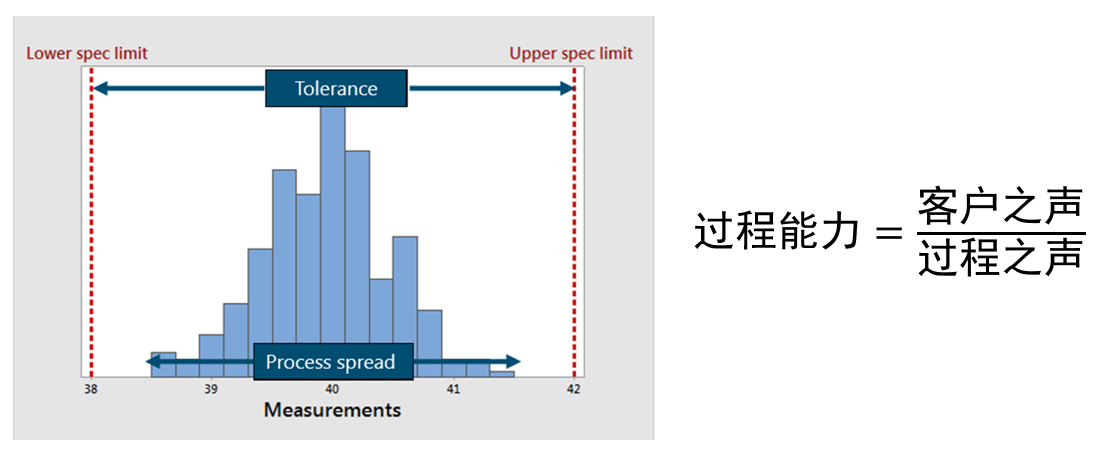
介绍“ISO方法”之前,我们首先来回顾一下能力分析的含义(如下图所示)。
其中,“客户之声”就是客户给定的公差带宽(USL-LSL),关键是怎么得到“过程之声”。
回想一下,如果数据服从正态分布,我们是怎么估计“过程之声”的?用正态分布的均值做为中心位置,用平均值±3标准差来构造一个99.73%的区间来做为“过程之声”的估计。
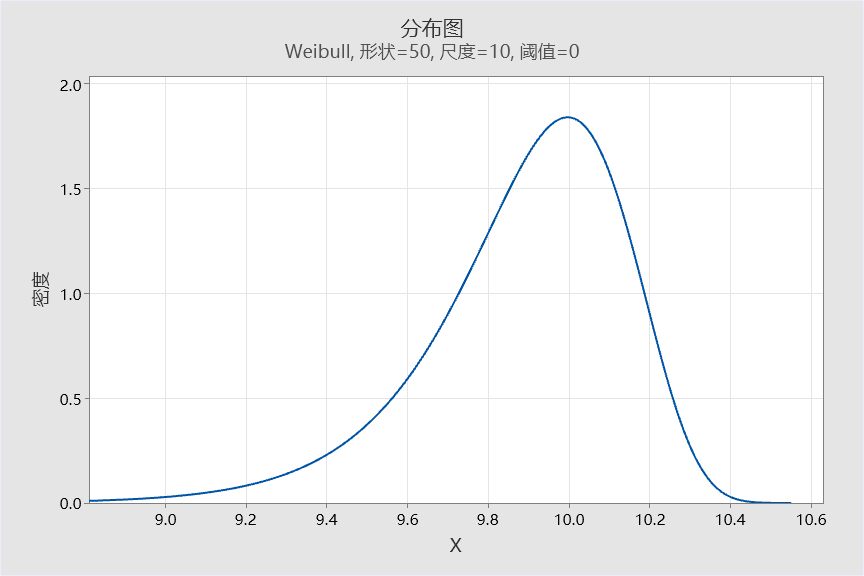
那如果是非正态数据呢,我们是不是也可以想办法来获得“过程之声”?但是很多非正态数据的分布不像正态分布那样是对称的(如下面的Weibull分布)。
那么这时候怎么获得中心位置和99.73%的区间呢?我们可以借助“ISO算法”通过计算分位数方法来估计“过程之声”。
说明:
表示指定分布的第0.99865个百分位数(太专业了,看不懂?直白一点说,分布选择不同,计算出来的结果不一样,所以我们需要找到合适的分布)。说到这里我相信大家应该理解了为什么在用Minitab做非正态数据能力分析时需要我们先指定分布了。
拟合其他分布法(ISO方法)计算
基于以上分析,我们可以通过以下三步骤来计算非正态数据的过程能力。
找到合适的分布(除正态分布外有13种选择),怎么确定哪种分布拟合的比较好呢?我们可以利用Minitab中的“个体分布标识”功能。
确定好分布后,第二步就是计算出对应分布的三个百分位数:0.5分位数、0.99865分位数和0.00135分位数(我们可以通过“概率分布图”计算这三个百分位数)。
把计算出来的三个百分位数带入“ISO方法”的公式得到Pp和Ppk。
收起阅读 »
非正态解决方案
如果您使用为正态数据设计的能力分析,您的数据必须服从正态分布。
对于上面的这些公式,我相信很多朋友比较熟悉(不同教材在公式写法和叫法上可能稍微不同),但我们今天讨论的不是这组公式,为什么呢?因为上面这些公式只适用于正态数据,而我们今天想分享的是非正态数据的能力分析。
对于非正态数据,我们可以通过以下方法来获得准确描述生成非正态数据的过程的能力指数。
正如你所看到的,解决方法有很多,当然方法选择不同结果肯定是有差异的,那么问题又来了,哪个方法是比较合适的呢?别急,我们可以先参考以下路径图帮助我们选择。
在上一篇文章中我们分享了变换的方法(Box-Cox变换),在这篇文章中,我们打算找到拟合数据的合适分布(除了正态分布外,Minitab在这里还提供了其他13种分布),采用非正态的方法来计算Ppk(注意,由于是非正态分布,这时候就无法计算Cp/CpK了)。
拟合其他分布法(ISO方法)原理
对于非正态数据,Minitab后台提供两种算法(21版本中,默认算法为“Z值法”)
但是,我们今天要分享的是“ISO方法”,原因很简单,这种算法大家在六西格玛相关课程和教材中其实学过了(先混个脸熟)。
介绍“ISO方法”之前,我们首先来回顾一下能力分析的含义(如下图所示)。
其中,“客户之声”就是客户给定的公差带宽(USL-LSL),关键是怎么得到“过程之声”。
回想一下,如果数据服从正态分布,我们是怎么估计“过程之声”的?用正态分布的均值做为中心位置,用平均值±3标准差来构造一个99.73%的区间来做为“过程之声”的估计。
那如果是非正态数据呢,我们是不是也可以想办法来获得“过程之声”?但是很多非正态数据的分布不像正态分布那样是对称的(如下面的Weibull分布)。
那么这时候怎么获得中心位置和99.73%的区间呢?我们可以借助“ISO算法”通过计算分位数方法来估计“过程之声”。
说明:
表示指定分布的第0.99865个百分位数(太专业了,看不懂?直白一点说,分布选择不同,计算出来的结果不一样,所以我们需要找到合适的分布)。说到这里我相信大家应该理解了为什么在用Minitab做非正态数据能力分析时需要我们先指定分布了。
拟合其他分布法(ISO方法)计算
基于以上分析,我们可以通过以下三步骤来计算非正态数据的过程能力。
找到合适的分布(除正态分布外有13种选择),怎么确定哪种分布拟合的比较好呢?我们可以利用Minitab中的“个体分布标识”功能。
确定好分布后,第二步就是计算出对应分布的三个百分位数:0.5分位数、0.99865分位数和0.00135分位数(我们可以通过“概率分布图”计算这三个百分位数)。
把计算出来的三个百分位数带入“ISO方法”的公式得到Pp和Ppk。
收起阅读 »
方差分析在等离子蚀刻中的应用
一、案例背景
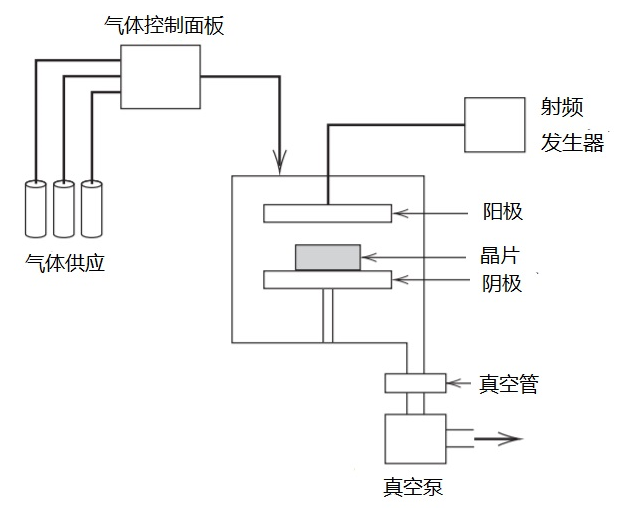
在集成电路的许多生产步骤中,晶片被一层材料(如二氧化硅或某种金属)完全覆盖。通过对掩模的蚀刻有选择性地除去不需要的材料,从而创建电路模板、电互连以及必须扩散的或者金属沉积的区域。等离子蚀刻工序在这个操作中被广泛使用,特别是在几何对象比较小的情况下的应用。下图展示了一种典型的单晶片蚀刻设备的重要特征。特此说明:案例来自蒙哥马利的《实验设计与分析》一书。
射频(RF)发生器提供能源使得电极之间的间隙产生等离子,等离子体的化学种类是由所使用的特定气体决定的。碳氟化合物,比如CF4(四氟甲烷)或C2F6(六氟乙烷),通常被用在等离子蚀刻上。但是根据应用情况的不同,也常使用其他的气体或混合气体。
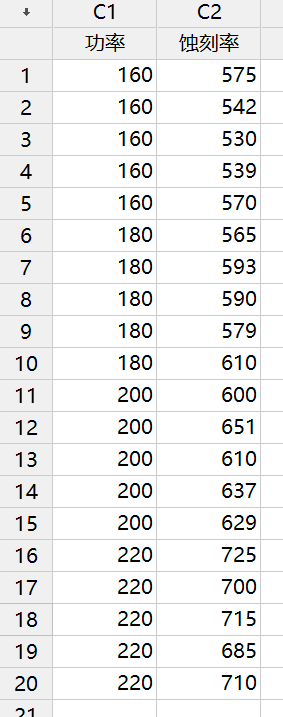
工程师要研究这套设备的RF功率设置与蚀刻率间的关系。实验目的是开发工程师要确定RF功率设置是否影响蚀刻率。她选定了气体(C2F6)和间隙(0.80 cm),想检验RF功率的4个水平:160W,180W,200W和220W。她决定在RF功率的每个水平上检验5个晶片。
这是一个因子水平为4和重复次数为5的单因子实验。这20个试验都是按照随机顺序进行的。
二、分析之前注意事项
一个好的试验设计分析,重点和难点往往不是在如何“分析”它(我相信通过本次案例,您也会借助Minitab做方差分析),而是在于如何“设计”这个试验,如何制定数据收集计划。对于设计得很差的试验,你做不了任何分析。你只能搬出具尸体,找出他的死亡原因。
Fisher曾经说过设计一个试验就像和魔鬼玩机会游戏一样,你无法预测他会使出什么样的高招让你的努力作废。在单晶片蚀刻中亦是如此,为防止未知讨厌变量的影响,随机化试验顺序是必要的,因为实验中讨厌变量的变化也许会超出控制范围。从而损害实验结果。为了方便大家对随机化的理解,请参考如下说明图。
知道了随机化的重要性,哪如何做到随机化呢?我发现很多朋友喜欢按照顺序做试验(先把功率为160的五次试验做完,再做180的,再做200的,最后再做功率为220的五次试验),这就不是我们所说的随机化顺序了。这种按照顺序方式做试验,最后的统计结论往往会变成管理者会议上的争论(我会在后续文章中分享这个故事)。
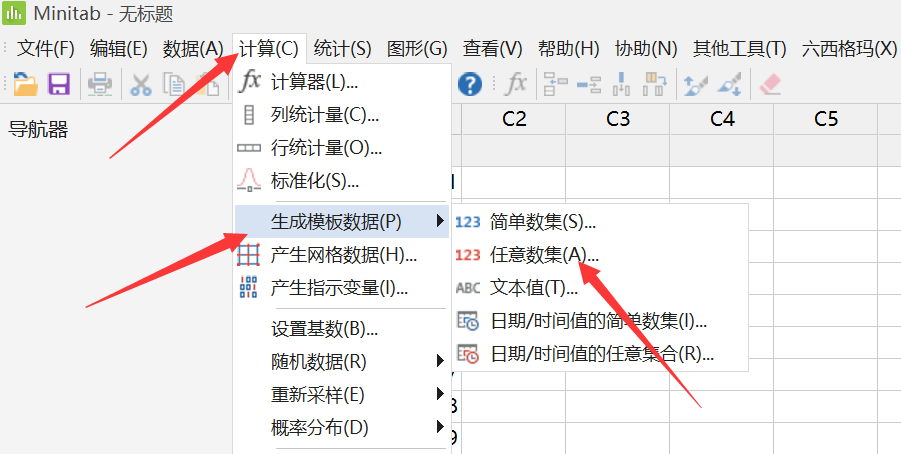
为了随机化,我们可以在Minitab中执行以下操作:
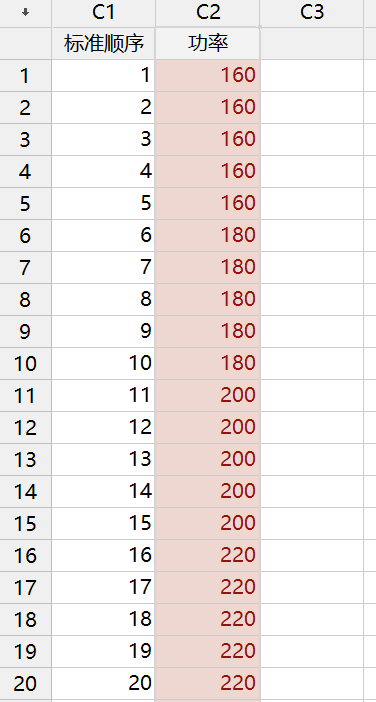
1.首先我们新建一“标准顺序”列,编号从1到20。
计算-生成模板数据-简单数集
2.计算-生成模板数据-任意数集
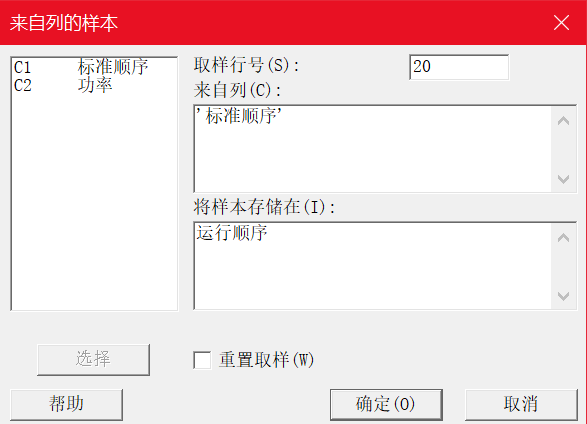
3.计算-随机数据-来自列的样本
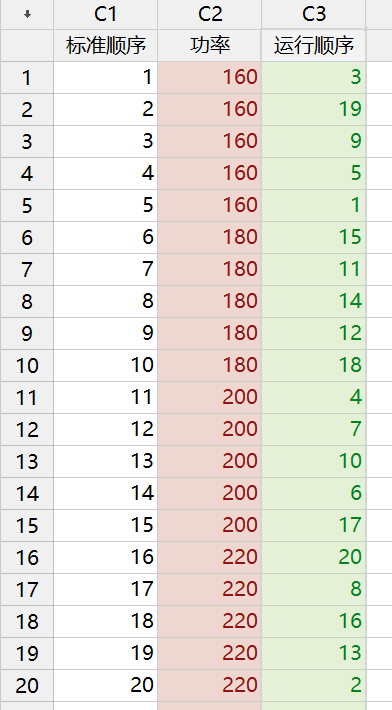
我们按照生成的随机化顺序(C3列运行序)做试验,第一次做功率为160的,第二次做功率为220的……(试验都做了,钱都花了,就不要想着偷懒了)。
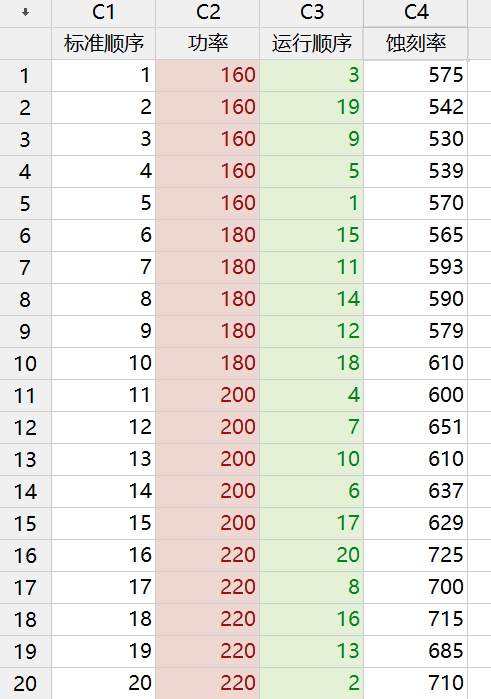
最终,得到以上试验数据(按照随机化顺序做的)。
三、Minitab操作步骤
在这里我们是想对单因子(功率)4个水平(160、180、200、220)下的蚀刻率均值做比较,这里我们可以使用方差分析。
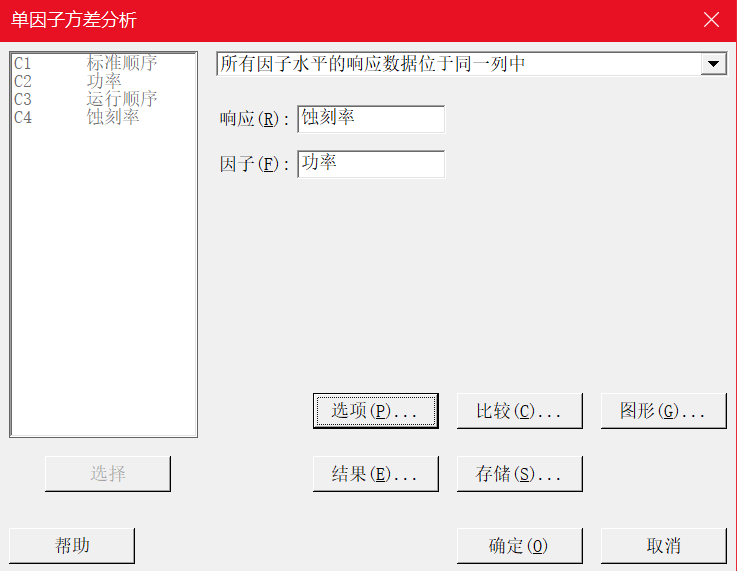
1.路径:统计-方差分析-单因子
2.Minitab结果解释
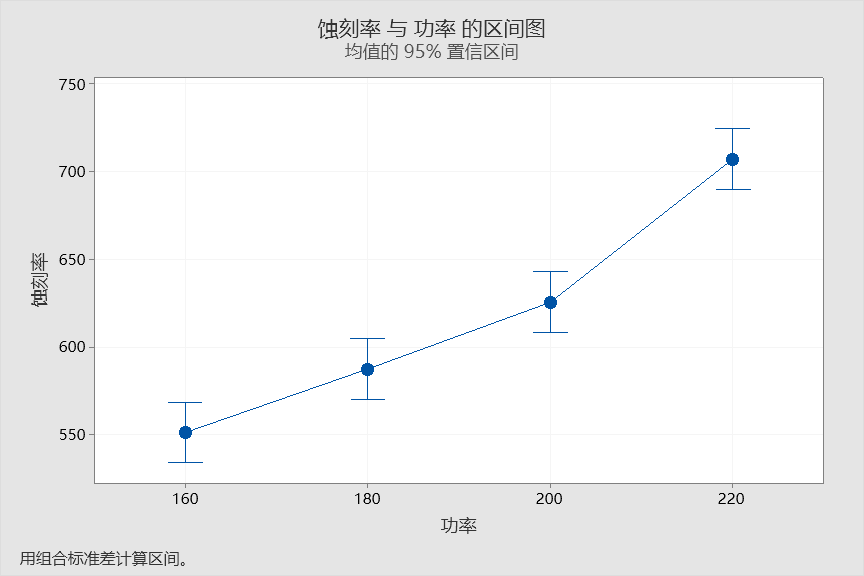
从“方差分析”表中,我们看到检验的P值等于0,小于0.05,故拒绝所有均值都相等的原假设,从而得到4个功率下蚀刻率均值有显著差异的结论。Minitab还同步输出了下面的区间图,从图中可以发现随着功率增大蚀刻率增大。
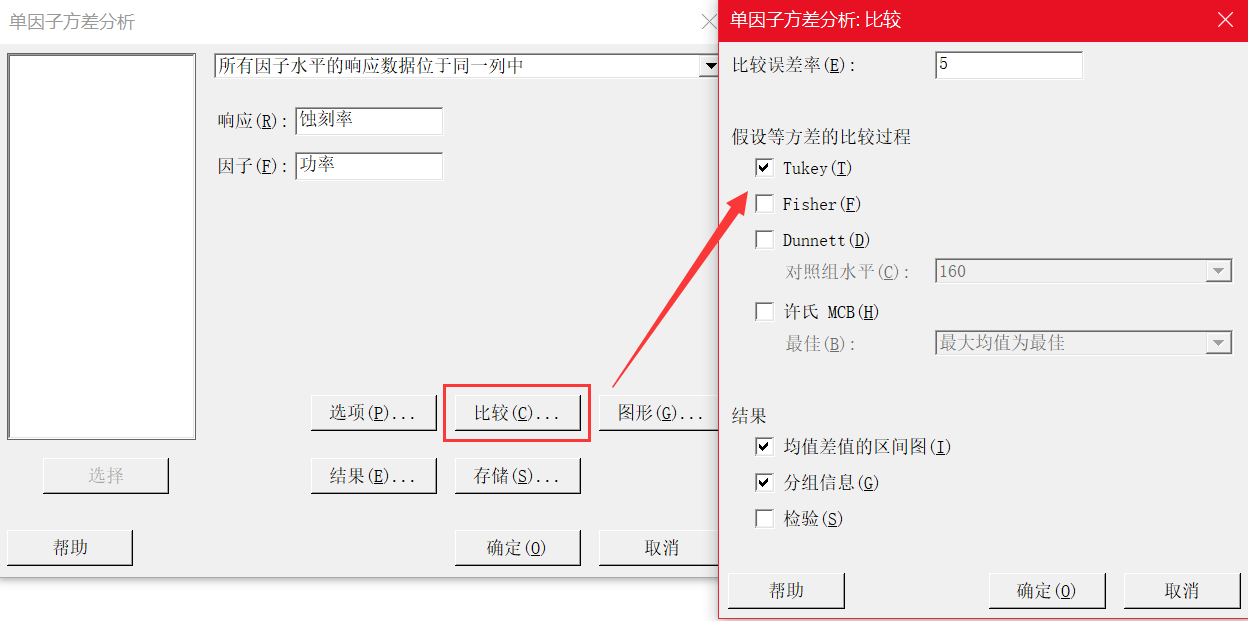
当然,你也可以进一步做多重比较。
四、小结
本篇文章着重向大家强调了试验中“随机化”的重要性以及如何安排随机化试验,我也希望大家能够在后续试验安排做到随机化(我知道,这确实不容易)。一个研究所需要的准备工作远比选择一个统计设计重要得多,统计基于你试验收集的数据,它不会撒谎。但如果试验本身就安排不合理(如没有随机化),利用这个试验获得的数据执行统计分析,那么这时候得到的统计结论有多少能够反映实际生产状况就不得而知了。 收起阅读 »
在集成电路的许多生产步骤中,晶片被一层材料(如二氧化硅或某种金属)完全覆盖。通过对掩模的蚀刻有选择性地除去不需要的材料,从而创建电路模板、电互连以及必须扩散的或者金属沉积的区域。等离子蚀刻工序在这个操作中被广泛使用,特别是在几何对象比较小的情况下的应用。下图展示了一种典型的单晶片蚀刻设备的重要特征。特此说明:案例来自蒙哥马利的《实验设计与分析》一书。
射频(RF)发生器提供能源使得电极之间的间隙产生等离子,等离子体的化学种类是由所使用的特定气体决定的。碳氟化合物,比如CF4(四氟甲烷)或C2F6(六氟乙烷),通常被用在等离子蚀刻上。但是根据应用情况的不同,也常使用其他的气体或混合气体。
工程师要研究这套设备的RF功率设置与蚀刻率间的关系。实验目的是开发工程师要确定RF功率设置是否影响蚀刻率。她选定了气体(C2F6)和间隙(0.80 cm),想检验RF功率的4个水平:160W,180W,200W和220W。她决定在RF功率的每个水平上检验5个晶片。
这是一个因子水平为4和重复次数为5的单因子实验。这20个试验都是按照随机顺序进行的。
二、分析之前注意事项
一个好的试验设计分析,重点和难点往往不是在如何“分析”它(我相信通过本次案例,您也会借助Minitab做方差分析),而是在于如何“设计”这个试验,如何制定数据收集计划。对于设计得很差的试验,你做不了任何分析。你只能搬出具尸体,找出他的死亡原因。
Fisher曾经说过设计一个试验就像和魔鬼玩机会游戏一样,你无法预测他会使出什么样的高招让你的努力作废。在单晶片蚀刻中亦是如此,为防止未知讨厌变量的影响,随机化试验顺序是必要的,因为实验中讨厌变量的变化也许会超出控制范围。从而损害实验结果。为了方便大家对随机化的理解,请参考如下说明图。
知道了随机化的重要性,哪如何做到随机化呢?我发现很多朋友喜欢按照顺序做试验(先把功率为160的五次试验做完,再做180的,再做200的,最后再做功率为220的五次试验),这就不是我们所说的随机化顺序了。这种按照顺序方式做试验,最后的统计结论往往会变成管理者会议上的争论(我会在后续文章中分享这个故事)。
为了随机化,我们可以在Minitab中执行以下操作:
1.首先我们新建一“标准顺序”列,编号从1到20。
计算-生成模板数据-简单数集
2.计算-生成模板数据-任意数集
3.计算-随机数据-来自列的样本
我们按照生成的随机化顺序(C3列运行序)做试验,第一次做功率为160的,第二次做功率为220的……(试验都做了,钱都花了,就不要想着偷懒了)。
最终,得到以上试验数据(按照随机化顺序做的)。
三、Minitab操作步骤
在这里我们是想对单因子(功率)4个水平(160、180、200、220)下的蚀刻率均值做比较,这里我们可以使用方差分析。
1.路径:统计-方差分析-单因子
2.Minitab结果解释
从“方差分析”表中,我们看到检验的P值等于0,小于0.05,故拒绝所有均值都相等的原假设,从而得到4个功率下蚀刻率均值有显著差异的结论。Minitab还同步输出了下面的区间图,从图中可以发现随着功率增大蚀刻率增大。
当然,你也可以进一步做多重比较。
四、小结
本篇文章着重向大家强调了试验中“随机化”的重要性以及如何安排随机化试验,我也希望大家能够在后续试验安排做到随机化(我知道,这确实不容易)。一个研究所需要的准备工作远比选择一个统计设计重要得多,统计基于你试验收集的数据,它不会撒谎。但如果试验本身就安排不合理(如没有随机化),利用这个试验获得的数据执行统计分析,那么这时候得到的统计结论有多少能够反映实际生产状况就不得而知了。 收起阅读 »
测量系统一致性分析 | 这个汤真的那么辣吗?
熊妈妈已经忍无可忍了。最近一次关于她做的汤有多辣的争论以张牙舞爪而结束,而且把小女孩吓坏了。
熊妈妈认为问题出在小女孩身上。自从有了金凤花姑娘之后,所有人都无法就任何事情达成一致。床不是太软就是太硬。粥不是太烫就是太凉。今晚,金凤花姑娘抱怨汤太辣,熊爸爸抱怨汤不够辣。
为了使家庭恢复安宁,熊妈妈觉得小女孩需要离开。但是,每当熊妈妈提到这点时,熊爸爸就会跑过去为金凤花姑娘辩护。熊妈妈需要使用数据来为自己辩护,她明白该怎么做:使用一种名为“属性一致性分析”的测量系统分析。熊妈妈知道,使用 Minitab中的“协助”会使事情变得简单容易。
首先,她煮了六份汤。在其中的三份汤中,熊妈妈仅添加了足够的胡椒粉和香料,使汤美味但不会太辣。她在其余三份汤中加了过量的辣椒酱。
接着,熊妈妈使用 Minitab来设置、收集和分析数据,她希望确定为什么家庭成员如此频繁地出现意见不一致。
设置属性一致性分析
选择协助 > 测量系统分析 (MSA)…
“协助”显示一个决策树,该决策树中包括用于“评价”数据的 MSA。
熊妈妈打算让每个家庭成员都品尝六份不同的汤,并让他们评价是好(“好喝!”)还是差(“难喝!”)。每个评价者对每份汤都品尝 4 次,因此熊妈妈不仅能够查看不同检验者的意见是否一致,还能查看每个检验者每次品尝后的评价是否一致。
但是,她的数据收集计划能够满足此分析的需要吗?单击“属性一致性工作表”下面的“更多…”即可显示一列需要检查的要求。例如,“协助”建议评价者对相同数量的好和差项目进行评分,还建议至少有 3 个评价者,熊妈妈的计划中涵盖了这两项要求。
现在,熊妈妈确信她的计划非常恰当。她单击“返回”,然后单击“属性一致性工作表”并按如下所示填写对话框:
在单击“确定”之后,Minitab 将针对每个评价者和每份汤生成一组(共四个)随机试验,并创建一个匹配的数据表。
Minitab 还允许打印一整套随时可用的数据收集表单(每个试验和评价者有一份对应的表单)。
接着,熊妈妈加热这六份汤,并让每个检验者按照 Minitab 所指定的随机顺序对每份汤品尝四次。然后,她只需将结果输入到其数据表的相应列中就可以了:
分析数据
将结果输入到工作表中之后,熊妈妈可以继续进行分析。返回到协助 > 测量系统分析 (MSA)…,但这一次的目标是分析数据,而不是设置研究:
按如上所示填写对话框,单击“确定”。Minitab 将生成所有输出,熊妈妈需要使用这些输出来为自己辩护。
汇总报告显示,总体而言,家庭成员正确识别汤辛辣程度的正确率仅为 75%。按评价者计算的准确度百分比显示每个评价者对汤进行识别的准确度。熊妈妈和熊宝宝的得分最高,他们的准确度分别为 95.8% 和 87.5%。熊爸爸的准确度为 79.2%,不算太低。
但是,金凤花姑娘的准确度为 37.5%,很低。
“协助”的准确度报告为熊妈妈提供了有关每个评价者表现的具体细节。准确度报告右侧的按评价者计算的准确度百分比图和标准图显示,在三头熊中,每头熊都非常擅长识别美味的汤,但是,金凤花姑娘正确识别出美味的汤的概率不到 20%。
“协助”还有另外两个输出——“误分类报告”和“报告卡”。
证据在汤里
通过属性一致性分析的结果,可以清楚地判定有关汤辣不辣的大多数不一致源自何处,以及(按照熊妈妈的观点)不一致应当在何处终结。使用由“协助”创建的简单图形,甚至连熊爸爸也可以轻松看出,金凤花姑娘对汤的评价分歧可能会导致家庭成员产生冲突。
无论您喜欢清淡的汤还是喜欢超辣的汤,您都已经成功完成了此测量系统分析。您已了解如何创建属性一致性分析工作表,以及如何分析您收集的数据以使用“协助”来确定评价者在何处一致,在何处不一致。 收起阅读 »
熊妈妈认为问题出在小女孩身上。自从有了金凤花姑娘之后,所有人都无法就任何事情达成一致。床不是太软就是太硬。粥不是太烫就是太凉。今晚,金凤花姑娘抱怨汤太辣,熊爸爸抱怨汤不够辣。
为了使家庭恢复安宁,熊妈妈觉得小女孩需要离开。但是,每当熊妈妈提到这点时,熊爸爸就会跑过去为金凤花姑娘辩护。熊妈妈需要使用数据来为自己辩护,她明白该怎么做:使用一种名为“属性一致性分析”的测量系统分析。熊妈妈知道,使用 Minitab中的“协助”会使事情变得简单容易。
首先,她煮了六份汤。在其中的三份汤中,熊妈妈仅添加了足够的胡椒粉和香料,使汤美味但不会太辣。她在其余三份汤中加了过量的辣椒酱。
接着,熊妈妈使用 Minitab来设置、收集和分析数据,她希望确定为什么家庭成员如此频繁地出现意见不一致。
设置属性一致性分析
选择协助 > 测量系统分析 (MSA)…
“协助”显示一个决策树,该决策树中包括用于“评价”数据的 MSA。
熊妈妈打算让每个家庭成员都品尝六份不同的汤,并让他们评价是好(“好喝!”)还是差(“难喝!”)。每个评价者对每份汤都品尝 4 次,因此熊妈妈不仅能够查看不同检验者的意见是否一致,还能查看每个检验者每次品尝后的评价是否一致。
但是,她的数据收集计划能够满足此分析的需要吗?单击“属性一致性工作表”下面的“更多…”即可显示一列需要检查的要求。例如,“协助”建议评价者对相同数量的好和差项目进行评分,还建议至少有 3 个评价者,熊妈妈的计划中涵盖了这两项要求。
现在,熊妈妈确信她的计划非常恰当。她单击“返回”,然后单击“属性一致性工作表”并按如下所示填写对话框:
在单击“确定”之后,Minitab 将针对每个评价者和每份汤生成一组(共四个)随机试验,并创建一个匹配的数据表。
Minitab 还允许打印一整套随时可用的数据收集表单(每个试验和评价者有一份对应的表单)。
接着,熊妈妈加热这六份汤,并让每个检验者按照 Minitab 所指定的随机顺序对每份汤品尝四次。然后,她只需将结果输入到其数据表的相应列中就可以了:
分析数据
将结果输入到工作表中之后,熊妈妈可以继续进行分析。返回到协助 > 测量系统分析 (MSA)…,但这一次的目标是分析数据,而不是设置研究:
按如上所示填写对话框,单击“确定”。Minitab 将生成所有输出,熊妈妈需要使用这些输出来为自己辩护。
汇总报告显示,总体而言,家庭成员正确识别汤辛辣程度的正确率仅为 75%。按评价者计算的准确度百分比显示每个评价者对汤进行识别的准确度。熊妈妈和熊宝宝的得分最高,他们的准确度分别为 95.8% 和 87.5%。熊爸爸的准确度为 79.2%,不算太低。
但是,金凤花姑娘的准确度为 37.5%,很低。
“协助”的准确度报告为熊妈妈提供了有关每个评价者表现的具体细节。准确度报告右侧的按评价者计算的准确度百分比图和标准图显示,在三头熊中,每头熊都非常擅长识别美味的汤,但是,金凤花姑娘正确识别出美味的汤的概率不到 20%。
“协助”还有另外两个输出——“误分类报告”和“报告卡”。
证据在汤里
通过属性一致性分析的结果,可以清楚地判定有关汤辣不辣的大多数不一致源自何处,以及(按照熊妈妈的观点)不一致应当在何处终结。使用由“协助”创建的简单图形,甚至连熊爸爸也可以轻松看出,金凤花姑娘对汤的评价分歧可能会导致家庭成员产生冲突。
无论您喜欢清淡的汤还是喜欢超辣的汤,您都已经成功完成了此测量系统分析。您已了解如何创建属性一致性分析工作表,以及如何分析您收集的数据以使用“协助”来确定评价者在何处一致,在何处不一致。 收起阅读 »
测量系统一致性分析 | 这个汤真的那么辣吗?
熊妈妈已经忍无可忍了。最近一次关于她做的汤有多辣的争论以张牙舞爪而结束,而且把小女孩吓坏了。
熊妈妈认为问题出在小女孩身上。自从有了金凤花姑娘之后,所有人都无法就任何事情达成一致。床不是太软就是太硬。粥不是太烫就是太凉。今晚,金凤花姑娘抱怨汤太辣,熊爸爸抱怨汤不够辣。
为了使家庭恢复安宁,熊妈妈觉得小女孩需要离开。但是,每当熊妈妈提到这点时,熊爸爸就会跑过去为金凤花姑娘辩护。熊妈妈需要使用数据来为自己辩护,她明白该怎么做:使用一种名为“属性一致性分析”的测量系统分析。熊妈妈知道,使用 Minitab中的“协助”会使事情变得简单容易。
首先,她煮了六份汤。在其中的三份汤中,熊妈妈仅添加了足够的胡椒粉和香料,使汤美味但不会太辣。她在其余三份汤中加了过量的辣椒酱。
接着,熊妈妈使用 Minitab来设置、收集和分析数据,她希望确定为什么家庭成员如此频繁地出现意见不一致。
设置属性一致性分析
选择协助 > 测量系统分析 (MSA)…
“协助”显示一个决策树,该决策树中包括用于“评价”数据的 MSA。
熊妈妈打算让每个家庭成员都品尝六份不同的汤,并让他们评价是好(“好喝!”)还是差(“难喝!”)。每个评价者对每份汤都品尝 4 次,因此熊妈妈不仅能够查看不同检验者的意见是否一致,还能查看每个检验者每次品尝后的评价是否一致。
但是,她的数据收集计划能够满足此分析的需要吗?单击“属性一致性工作表”下面的“更多…”即可显示一列需要检查的要求。例如,“协助”建议评价者对相同数量的好和差项目进行评分,还建议至少有 3 个评价者,熊妈妈的计划中涵盖了这两项要求。
现在,熊妈妈确信她的计划非常恰当。她单击“返回”,然后单击“属性一致性工作表”并按如下所示填写对话框:
在单击“确定”之后,Minitab 将针对每个评价者和每份汤生成一组(共四个)随机试验,并创建一个匹配的数据表。
Minitab 还允许打印一整套随时可用的数据收集表单(每个试验和评价者有一份对应的表单)。
接着,熊妈妈加热这六份汤,并让每个检验者按照 Minitab 所指定的随机顺序对每份汤品尝四次。然后,她只需将结果输入到其数据表的相应列中就可以了:
分析数据
将结果输入到工作表中之后,熊妈妈可以继续进行分析。返回到协助 > 测量系统分析 (MSA)…,但这一次的目标是分析数据,而不是设置研究:
按如上所示填写对话框,单击“确定”。Minitab 将生成所有输出,熊妈妈需要使用这些输出来为自己辩护。
汇总报告显示,总体而言,家庭成员正确识别汤辛辣程度的正确率仅为 75%。按评价者计算的准确度百分比显示每个评价者对汤进行识别的准确度。熊妈妈和熊宝宝的得分最高,他们的准确度分别为 95.8% 和 87.5%。熊爸爸的准确度为 79.2%,不算太低。
但是,金凤花姑娘的准确度为 37.5%,很低。
“协助”的准确度报告为熊妈妈提供了有关每个评价者表现的具体细节。准确度报告右侧的按评价者计算的准确度百分比图和标准图显示,在三头熊中,每头熊都非常擅长识别美味的汤,但是,金凤花姑娘正确识别出美味的汤的概率不到 20%。
“协助”还有另外两个输出——“误分类报告”和“报告卡”。
证据在汤里
通过属性一致性分析的结果,可以清楚地判定有关汤辣不辣的大多数不一致源自何处,以及(按照熊妈妈的观点)不一致应当在何处终结。使用由“协助”创建的简单图形,甚至连熊爸爸也可以轻松看出,金凤花姑娘对汤的评价分歧可能会导致家庭成员产生冲突。
无论您喜欢清淡的汤还是喜欢超辣的汤,您都已经成功完成了此测量系统分析。您已了解如何创建属性一致性分析工作表,以及如何分析您收集的数据以使用“协助”来确定评价者在何处一致,在何处不一致。 收起阅读 »
熊妈妈认为问题出在小女孩身上。自从有了金凤花姑娘之后,所有人都无法就任何事情达成一致。床不是太软就是太硬。粥不是太烫就是太凉。今晚,金凤花姑娘抱怨汤太辣,熊爸爸抱怨汤不够辣。
为了使家庭恢复安宁,熊妈妈觉得小女孩需要离开。但是,每当熊妈妈提到这点时,熊爸爸就会跑过去为金凤花姑娘辩护。熊妈妈需要使用数据来为自己辩护,她明白该怎么做:使用一种名为“属性一致性分析”的测量系统分析。熊妈妈知道,使用 Minitab中的“协助”会使事情变得简单容易。
首先,她煮了六份汤。在其中的三份汤中,熊妈妈仅添加了足够的胡椒粉和香料,使汤美味但不会太辣。她在其余三份汤中加了过量的辣椒酱。
接着,熊妈妈使用 Minitab来设置、收集和分析数据,她希望确定为什么家庭成员如此频繁地出现意见不一致。
设置属性一致性分析
选择协助 > 测量系统分析 (MSA)…
“协助”显示一个决策树,该决策树中包括用于“评价”数据的 MSA。
熊妈妈打算让每个家庭成员都品尝六份不同的汤,并让他们评价是好(“好喝!”)还是差(“难喝!”)。每个评价者对每份汤都品尝 4 次,因此熊妈妈不仅能够查看不同检验者的意见是否一致,还能查看每个检验者每次品尝后的评价是否一致。
但是,她的数据收集计划能够满足此分析的需要吗?单击“属性一致性工作表”下面的“更多…”即可显示一列需要检查的要求。例如,“协助”建议评价者对相同数量的好和差项目进行评分,还建议至少有 3 个评价者,熊妈妈的计划中涵盖了这两项要求。
现在,熊妈妈确信她的计划非常恰当。她单击“返回”,然后单击“属性一致性工作表”并按如下所示填写对话框:
在单击“确定”之后,Minitab 将针对每个评价者和每份汤生成一组(共四个)随机试验,并创建一个匹配的数据表。
Minitab 还允许打印一整套随时可用的数据收集表单(每个试验和评价者有一份对应的表单)。
接着,熊妈妈加热这六份汤,并让每个检验者按照 Minitab 所指定的随机顺序对每份汤品尝四次。然后,她只需将结果输入到其数据表的相应列中就可以了:
分析数据
将结果输入到工作表中之后,熊妈妈可以继续进行分析。返回到协助 > 测量系统分析 (MSA)…,但这一次的目标是分析数据,而不是设置研究:
按如上所示填写对话框,单击“确定”。Minitab 将生成所有输出,熊妈妈需要使用这些输出来为自己辩护。
汇总报告显示,总体而言,家庭成员正确识别汤辛辣程度的正确率仅为 75%。按评价者计算的准确度百分比显示每个评价者对汤进行识别的准确度。熊妈妈和熊宝宝的得分最高,他们的准确度分别为 95.8% 和 87.5%。熊爸爸的准确度为 79.2%,不算太低。
但是,金凤花姑娘的准确度为 37.5%,很低。
“协助”的准确度报告为熊妈妈提供了有关每个评价者表现的具体细节。准确度报告右侧的按评价者计算的准确度百分比图和标准图显示,在三头熊中,每头熊都非常擅长识别美味的汤,但是,金凤花姑娘正确识别出美味的汤的概率不到 20%。
“协助”还有另外两个输出——“误分类报告”和“报告卡”。
证据在汤里
通过属性一致性分析的结果,可以清楚地判定有关汤辣不辣的大多数不一致源自何处,以及(按照熊妈妈的观点)不一致应当在何处终结。使用由“协助”创建的简单图形,甚至连熊爸爸也可以轻松看出,金凤花姑娘对汤的评价分歧可能会导致家庭成员产生冲突。
无论您喜欢清淡的汤还是喜欢超辣的汤,您都已经成功完成了此测量系统分析。您已了解如何创建属性一致性分析工作表,以及如何分析您收集的数据以使用“协助”来确定评价者在何处一致,在何处不一致。 收起阅读 »
二值响应DOE-汽车挡风玻璃断裂问题
二值响应DOE
传统实验设计的因子类型可以是连续型的也可以是文本型的,而响应变量都是连续型的,如我们想考察材料类型、注塑压力、注塑温度、冷却温度对绝缘强度的影响。现在Minitab 21中新增了二值响应DOE的功能,所谓二值响应就是结果只有两种可能,是/否,好/坏,合格/不合格。二值响应DOE,您可以在Minitab 21的以下分析中找到。
筛选设计
因子设计
响应曲面设计
问题背景
一家汽车制造商想观察由于外来物质损害挡风玻璃所产生的裂纹,他们考虑了三个因子:外来粒子的速度、粒子重量和玻璃供应商。
A: 颗粒的速度(mph),低水平:50, 高水平:60
B: 颗粒的重量(gram),低水平:20, 高水平:40
C: 挡风玻璃的供应商:低水平:A,高水平:B
数据收集
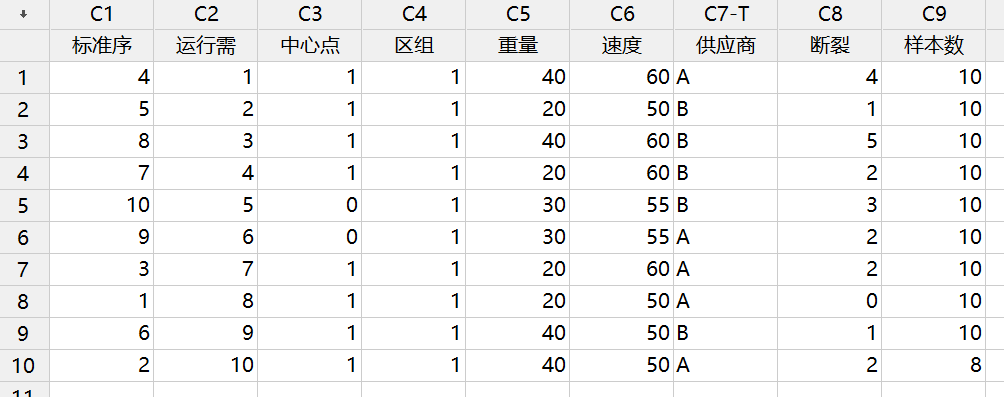
在一个特殊的设计实验房间里,一种颗粒被射向固定于20英尺远的挡风玻璃,一个检验员记录挡风玻璃是否产生裂纹,每种挡风玻璃只使用一次。制造商具有进行对100种挡风玻璃进行实验的资金、时间和材料,允许研究者试验10种挡风玻璃的样本大小。每8个因子的组合和两个中心点。然而,从供应商A只能获得48种挡风玻璃,因此,最后一轮实验只包括8种挡风玻璃样本。
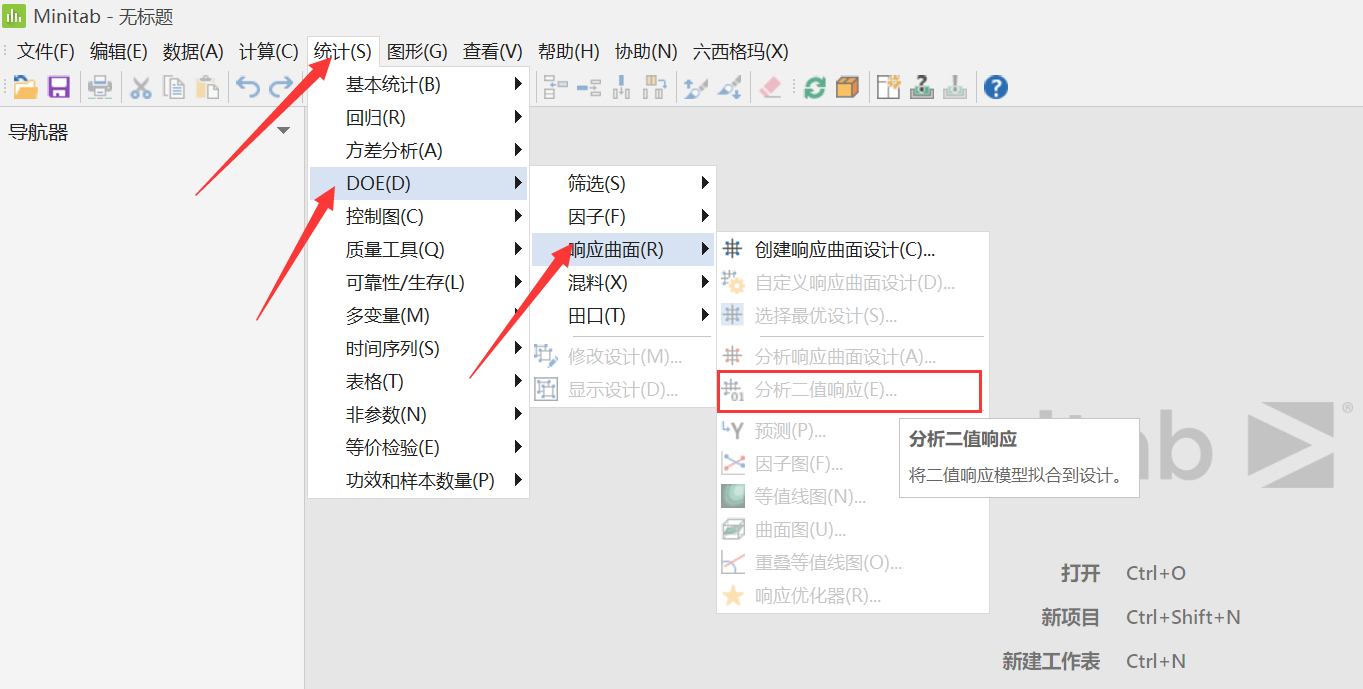
分析二值DOE
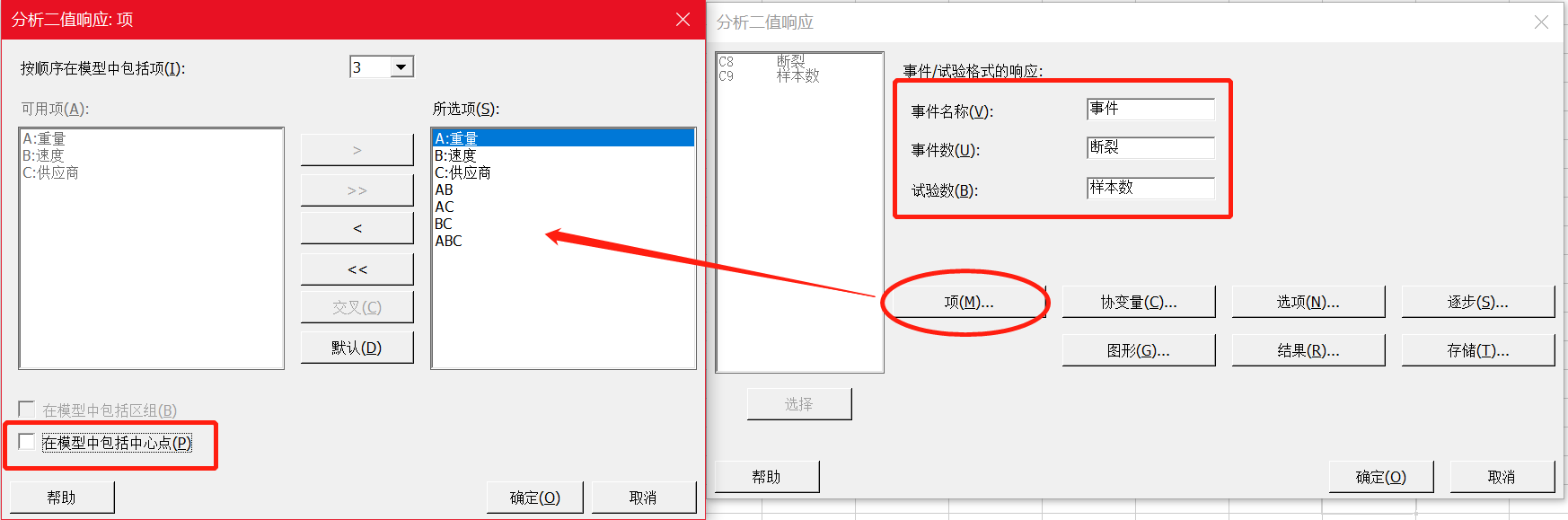
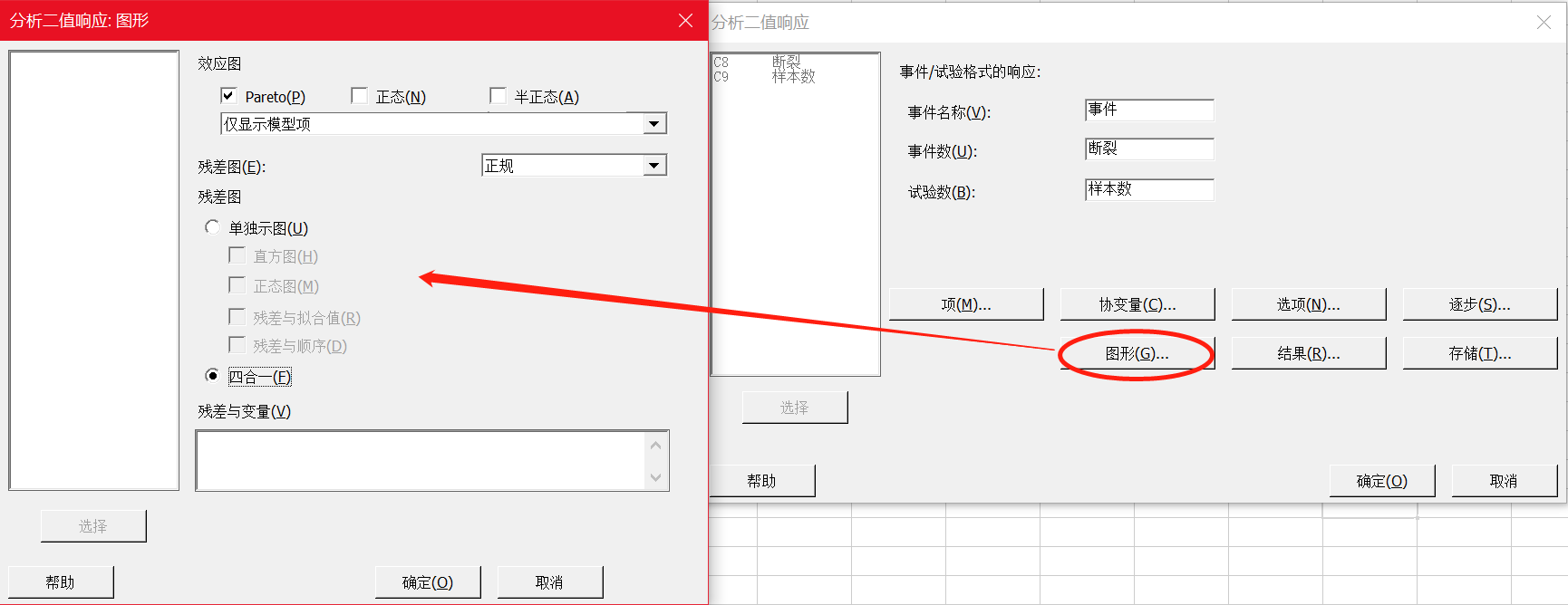
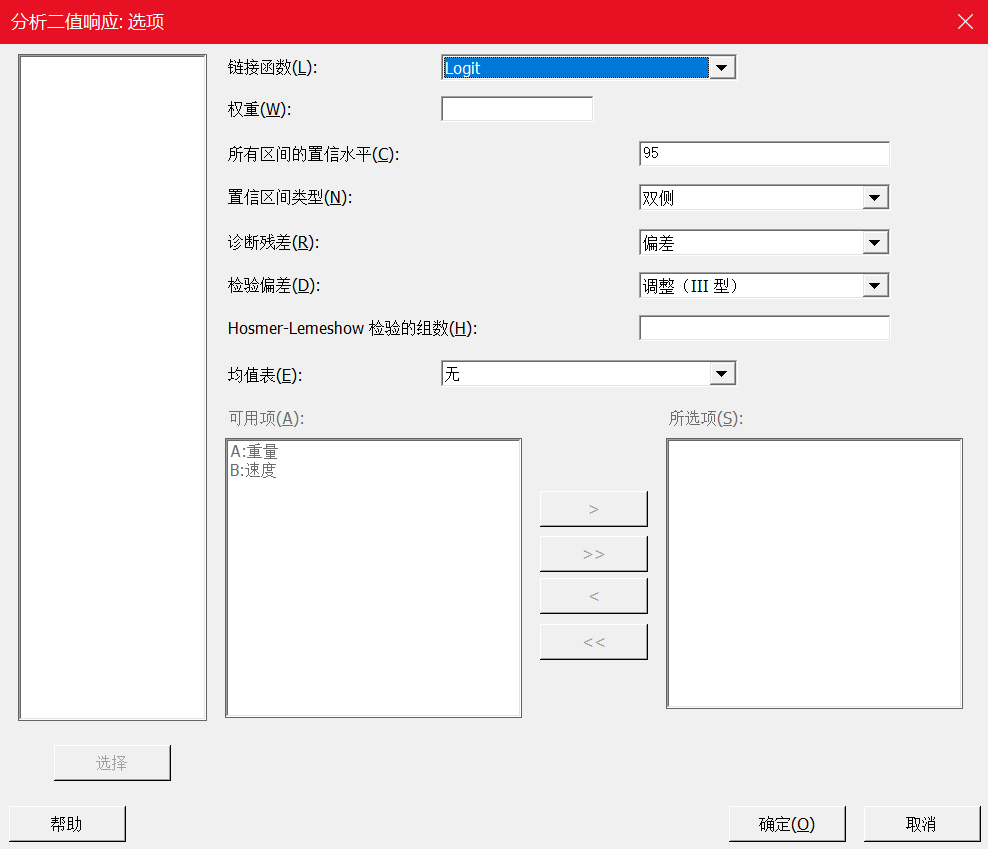
在Minitab 21的二值响应DOE分析种,除了主对话框跟经典实验设计有比较大区别以外,其他选项,比如“项”、“图形”中的设置是没有差别的。
在“项”中,我们第一次拟合模型时,把所有的项都考虑进来(在下面分析中有一个陷阱,请注意哦)。
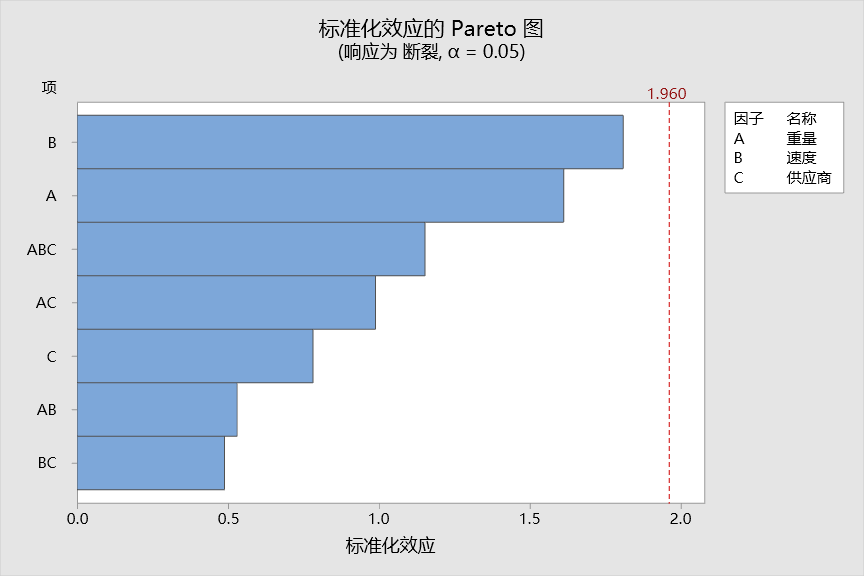
所有对话框点击确定后,得到如下结果。
注意:当我们把所有项都加入到模型中,这时候我们可以看到没有显著的项,此时不要急着下结论。这时候一般的做法是先删除高阶交互作用项。
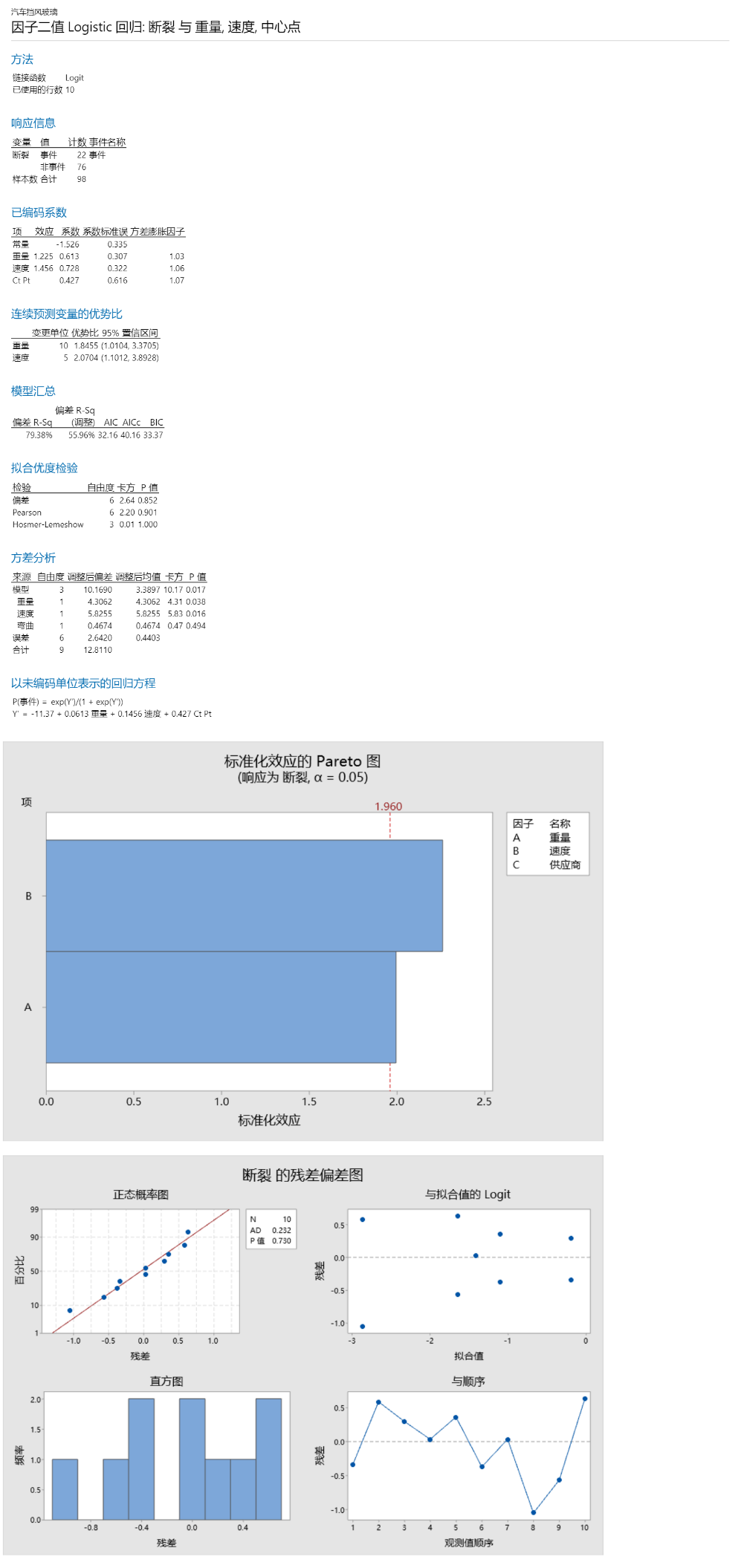
删除三阶交互作用项和所有二阶交互作用项以后,我们可以看到这时候A和B变成显著的了,C仍然不显著,在下一步优化中需要删除掉。我们得到以下的最终结果。
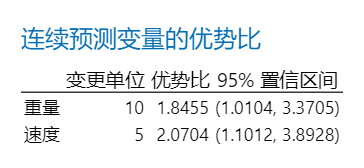
优势比
仅当您为具有二元响应的模型选择 logit 链接函数时才提供优势比。在这种情况下,优势比可用于解释预测变量与响应之间的关系。
连续预测变量的优势比:优势比大于 1 表示在预测变量越大,事件发生的几率越大。优势比小于 1 表示预测变量越大,事件发生的几率越小。在当前结果中,该模型使用颗粒的重量水平来预测汽车挡风玻璃是否断裂。在此示例中,挡风玻璃断裂为“事件”。每颗粒的重量为10gram,因此研究人员使用10gram作为一个单位变化。优势比约为1.8455。颗粒重量每增加一个单位,挡风玻璃断裂的比率就增加约1.8455倍。颗粒速度的优势比解释结果一样,不再赘述。
类别预测变量(当前结果没有)的优势比:对于类别预测变量,优势比可以比较事件在两个不同的预测变量水平发生的几率。Minitab 通过在水平 A 和水平 B 这两列中列出水平来设置比较。水平 B 是因子的参考水平。优势比大于 1 表示事件在水平 A 下发生的几率大。优势比小于 1 表示事件在水平 A 下发生的几率小。
结论
在Minitab 21中有了二值响应DOE分析,扩展了DOE的功能。当然,在实验设计中我们除了遇到二值响应DOE外,可能还会遇到残差分析有问题需要对响应变量做变换的DOE分析、带区组的实验设计分析等比较复杂的DOE问题。我们将在后续为大家一一分享,如果您还没有使用过Minitab 21,可以登陆Minitab官网下载30天免费试用版哦! 收起阅读 »
传统实验设计的因子类型可以是连续型的也可以是文本型的,而响应变量都是连续型的,如我们想考察材料类型、注塑压力、注塑温度、冷却温度对绝缘强度的影响。现在Minitab 21中新增了二值响应DOE的功能,所谓二值响应就是结果只有两种可能,是/否,好/坏,合格/不合格。二值响应DOE,您可以在Minitab 21的以下分析中找到。
筛选设计
因子设计
响应曲面设计
问题背景
一家汽车制造商想观察由于外来物质损害挡风玻璃所产生的裂纹,他们考虑了三个因子:外来粒子的速度、粒子重量和玻璃供应商。
A: 颗粒的速度(mph),低水平:50, 高水平:60
B: 颗粒的重量(gram),低水平:20, 高水平:40
C: 挡风玻璃的供应商:低水平:A,高水平:B
数据收集
在一个特殊的设计实验房间里,一种颗粒被射向固定于20英尺远的挡风玻璃,一个检验员记录挡风玻璃是否产生裂纹,每种挡风玻璃只使用一次。制造商具有进行对100种挡风玻璃进行实验的资金、时间和材料,允许研究者试验10种挡风玻璃的样本大小。每8个因子的组合和两个中心点。然而,从供应商A只能获得48种挡风玻璃,因此,最后一轮实验只包括8种挡风玻璃样本。
分析二值DOE
在Minitab 21的二值响应DOE分析种,除了主对话框跟经典实验设计有比较大区别以外,其他选项,比如“项”、“图形”中的设置是没有差别的。
在“项”中,我们第一次拟合模型时,把所有的项都考虑进来(在下面分析中有一个陷阱,请注意哦)。
所有对话框点击确定后,得到如下结果。
注意:当我们把所有项都加入到模型中,这时候我们可以看到没有显著的项,此时不要急着下结论。这时候一般的做法是先删除高阶交互作用项。
删除三阶交互作用项和所有二阶交互作用项以后,我们可以看到这时候A和B变成显著的了,C仍然不显著,在下一步优化中需要删除掉。我们得到以下的最终结果。
优势比
仅当您为具有二元响应的模型选择 logit 链接函数时才提供优势比。在这种情况下,优势比可用于解释预测变量与响应之间的关系。
连续预测变量的优势比:优势比大于 1 表示在预测变量越大,事件发生的几率越大。优势比小于 1 表示预测变量越大,事件发生的几率越小。在当前结果中,该模型使用颗粒的重量水平来预测汽车挡风玻璃是否断裂。在此示例中,挡风玻璃断裂为“事件”。每颗粒的重量为10gram,因此研究人员使用10gram作为一个单位变化。优势比约为1.8455。颗粒重量每增加一个单位,挡风玻璃断裂的比率就增加约1.8455倍。颗粒速度的优势比解释结果一样,不再赘述。
类别预测变量(当前结果没有)的优势比:对于类别预测变量,优势比可以比较事件在两个不同的预测变量水平发生的几率。Minitab 通过在水平 A 和水平 B 这两列中列出水平来设置比较。水平 B 是因子的参考水平。优势比大于 1 表示事件在水平 A 下发生的几率大。优势比小于 1 表示事件在水平 A 下发生的几率小。
结论
在Minitab 21中有了二值响应DOE分析,扩展了DOE的功能。当然,在实验设计中我们除了遇到二值响应DOE外,可能还会遇到残差分析有问题需要对响应变量做变换的DOE分析、带区组的实验设计分析等比较复杂的DOE问题。我们将在后续为大家一一分享,如果您还没有使用过Minitab 21,可以登陆Minitab官网下载30天免费试用版哦! 收起阅读 »
汽车行业准则:自信地采用 AIAG-VDA FMEA 方法
失效模式和效应分析(FMEA)是一种常见方法,用于制造和工程行业中找出设计、制造、装配过程、产品或服务中所有可能出现的差错。
尽管起源于军队,但随着时间推移,汽车行业已制定了 FMEA 的相关标准。因此,汽车行业的风险分析最佳实践已被许多其他行业采用并持续遵循。
多年来,汽车行业质量标准准则由两家权威组织制定:位于美国的汽车工业行动集团(AIAG)和位于德国的汽车工业协议(VDA)。
随着经济日益全球化,使得制造商从世界各地采购耗材和零件变得前所未有的简单。但是,一个行业内采用两套 FMEA 方法无疑会使效率降低,影响发展进程。例如,同时服务于北美和德国制造商的供应商,需要使用不同的标准对相同的零件进行评估,具体取决于零件的使用地区。同样,当制造商审核不同供应商时,不得不根据其地理位置使用不同的评分系统。这使得供应商比较变得既棘手又耗时,更重要的是,评估风险时更是如此!
总之,使用两套“标准”会导致混乱,并给全球供应商和制造商在产品开发和过程改进活动中,增加复杂性。
AIAG-VDA FMEA 关键更改
2019年,美国 AIAG 和德国 VDA 合作推出 FMEA 流程的标准化版本(强调预防并优先降低风险),为汽车行业的供应商提供一致的指南和准则。结果就是一个评分表,可满足整个行业中的制造商需求,从而减轻混乱的风险并减少重复工作。有了这套国际通用的准则,供应商只需管理一个单一的 FMEA 流程,即可满足世界各地所有客户的需求和期望。
相较于以前的区域手册(问题的严重性、发生频率和可检测性的权重相同),新的评分框架建立了一个等级体系。也就是说,问题的严重性将占据最大的权重,然后是发生的频率,最后是可检测性。换言之,新方法优先考虑严重问题,即使它们发生的频率相对较低并且易于检测;或者是危险性较低的问题,这些问题的发生可能会更频繁,或者更难被发现。
AIAG 与 VDA 合作为 FMEA 开发建立了全新的 7 步法,这 7 步可以分为三类。
步骤 1 至 3 与系统分析有关:
规划和准备
结构分析
功能分析
步骤 4 至 6 专注于失效分析和风险缓解:
失效分析
风险分析
优化
步骤 7 也是最后一步,将通过记录结果来解决风险沟通这个问题。
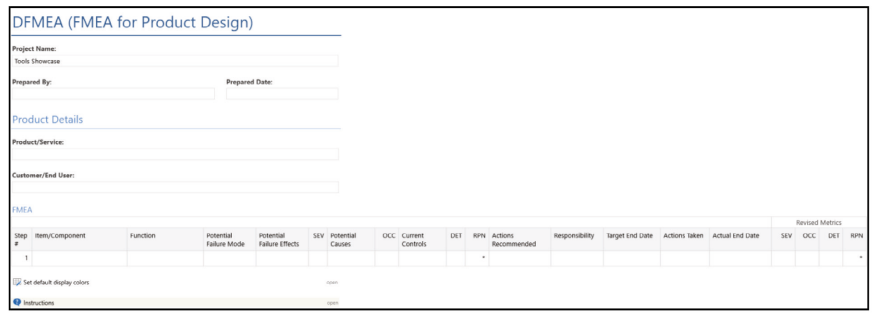
以下是设计失效模式效应分析(DFMEA)模板的预览,可在 Minitab Workspace® 和 Minitab EngageTM 中获得,是为支持最新的 AIAG-VDA FMEA 框架而创建。过程失效模式效应分析(PMFEA)模板也可在 Minitab Workspace® 和 Minitab EngageTM 中获得。请注意,虽然使用 DFMEA 和 PMFEA 在方法上存在显著差异,但两者都结合了 AIAG-VDA FMEA 7 步法。
Minitab 的 AIAG-VDA FMEA 模板如何为您提供帮助
在实施最新 AIAG-VDA FMEA 方法时,使用 FMEA 的汽车供应商必须考虑周全和彻底,同时要注意其修订后的评分框架以及更改后的方法和术语。
全面更新 FMEA 需要时间、理解和投入,但是利用 Minitab Workspace® 和 Minitab EngageTM 提供的设计专业的 DFMEA 和 PFMEA 表单模板,在确保您的 FMEA 与最新的行业标准保持一致时,您可以自信地更新您的风险分析过程。 收起阅读 »
尽管起源于军队,但随着时间推移,汽车行业已制定了 FMEA 的相关标准。因此,汽车行业的风险分析最佳实践已被许多其他行业采用并持续遵循。
多年来,汽车行业质量标准准则由两家权威组织制定:位于美国的汽车工业行动集团(AIAG)和位于德国的汽车工业协议(VDA)。
随着经济日益全球化,使得制造商从世界各地采购耗材和零件变得前所未有的简单。但是,一个行业内采用两套 FMEA 方法无疑会使效率降低,影响发展进程。例如,同时服务于北美和德国制造商的供应商,需要使用不同的标准对相同的零件进行评估,具体取决于零件的使用地区。同样,当制造商审核不同供应商时,不得不根据其地理位置使用不同的评分系统。这使得供应商比较变得既棘手又耗时,更重要的是,评估风险时更是如此!
总之,使用两套“标准”会导致混乱,并给全球供应商和制造商在产品开发和过程改进活动中,增加复杂性。
AIAG-VDA FMEA 关键更改
2019年,美国 AIAG 和德国 VDA 合作推出 FMEA 流程的标准化版本(强调预防并优先降低风险),为汽车行业的供应商提供一致的指南和准则。结果就是一个评分表,可满足整个行业中的制造商需求,从而减轻混乱的风险并减少重复工作。有了这套国际通用的准则,供应商只需管理一个单一的 FMEA 流程,即可满足世界各地所有客户的需求和期望。
相较于以前的区域手册(问题的严重性、发生频率和可检测性的权重相同),新的评分框架建立了一个等级体系。也就是说,问题的严重性将占据最大的权重,然后是发生的频率,最后是可检测性。换言之,新方法优先考虑严重问题,即使它们发生的频率相对较低并且易于检测;或者是危险性较低的问题,这些问题的发生可能会更频繁,或者更难被发现。
AIAG 与 VDA 合作为 FMEA 开发建立了全新的 7 步法,这 7 步可以分为三类。
步骤 1 至 3 与系统分析有关:
规划和准备
结构分析
功能分析
步骤 4 至 6 专注于失效分析和风险缓解:
失效分析
风险分析
优化
步骤 7 也是最后一步,将通过记录结果来解决风险沟通这个问题。
以下是设计失效模式效应分析(DFMEA)模板的预览,可在 Minitab Workspace® 和 Minitab EngageTM 中获得,是为支持最新的 AIAG-VDA FMEA 框架而创建。过程失效模式效应分析(PMFEA)模板也可在 Minitab Workspace® 和 Minitab EngageTM 中获得。请注意,虽然使用 DFMEA 和 PMFEA 在方法上存在显著差异,但两者都结合了 AIAG-VDA FMEA 7 步法。
Minitab 的 AIAG-VDA FMEA 模板如何为您提供帮助
在实施最新 AIAG-VDA FMEA 方法时,使用 FMEA 的汽车供应商必须考虑周全和彻底,同时要注意其修订后的评分框架以及更改后的方法和术语。
全面更新 FMEA 需要时间、理解和投入,但是利用 Minitab Workspace® 和 Minitab EngageTM 提供的设计专业的 DFMEA 和 PFMEA 表单模板,在确保您的 FMEA 与最新的行业标准保持一致时,您可以自信地更新您的风险分析过程。 收起阅读 »
可靠产品设计的5项技术03-估计基准可靠性
预估基准可靠性将帮助我们集中精力进行可靠性分析,确定必要的故障预防措施,以及确定潜在的成本和收益。
这项技术的目标包括:
1)核实(或验证)是否符合要求
2)提高对产品、过程、失效模式和机制的了解
3)识别缺陷(不足)
4)检测出需要改进设计的领域
产品的可靠性源于其子系统、组件和材料的可靠性:
系统可靠性 = f(组件可靠性)
为了实施这项技术,必须对系统及其功能、使用条件和要求具有清晰的了解。
我们可以根据现场数据(如果可靠且可追踪), 或失效物理分析方面的知识、类似产品的可靠性预测记录、模拟模型、可比子系统和组件的保修和试验数据,计算出子系统和组件的基准可靠性。为了成功完成您的基准可靠性评估,我们推荐 Minitab统计分析软件中的以下任意一种工具:
1)试验方案
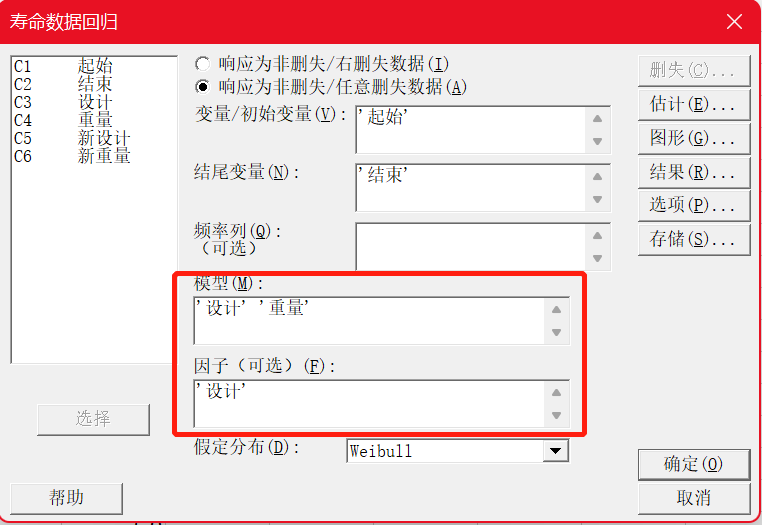
2)可修复系统分析
3)寿命数据回归
4)概率分析
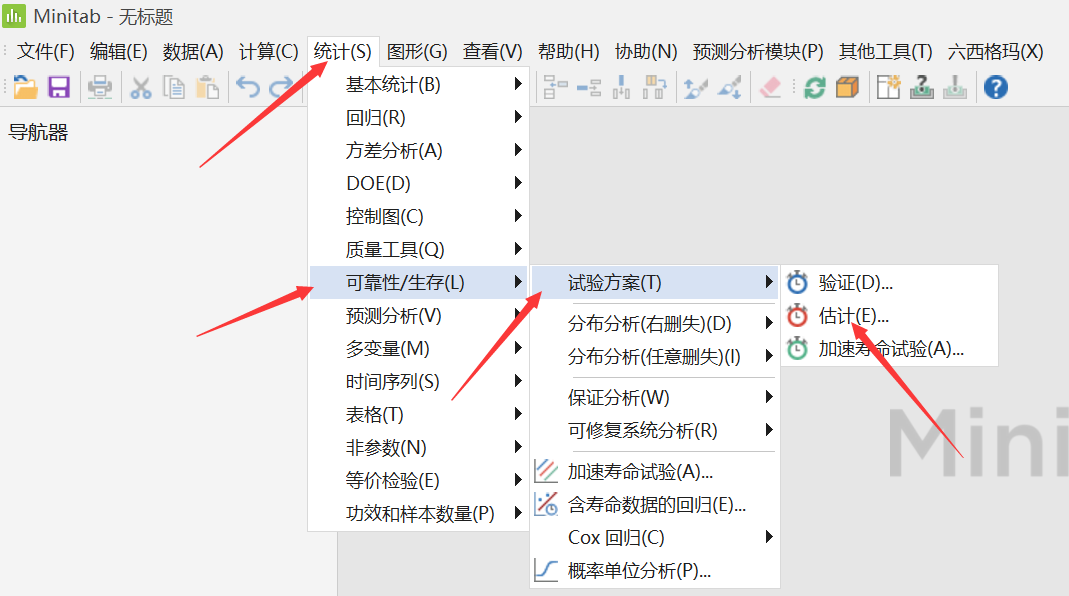
估计试验方案
在下面的示例中,我们说明了如何使用估计试验方案来开发一种新型的绝缘材料。
1.案例背景
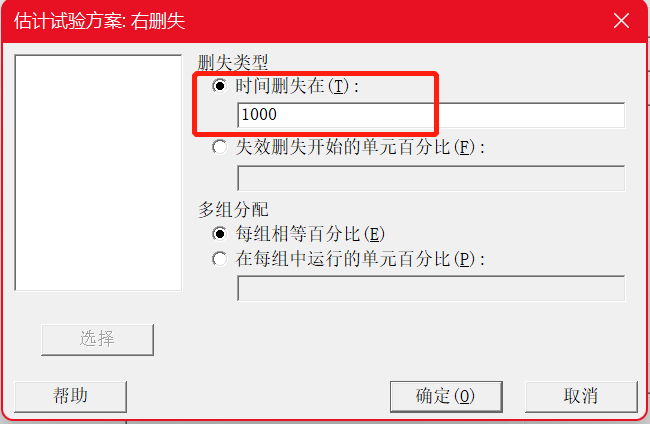
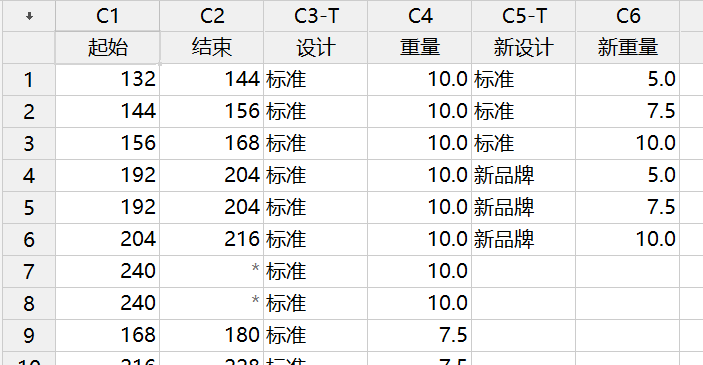
工程师正在研制一种新型绝缘材料。他们要确定当与要估计的下限的距离在 100、200 和 300 小时之内时,估计第10个百分位数所需的样本数量。工程师将针对小样本执行 1000 小时的可靠性检验。他们针对检验计划使用以下信息:
· 预期大约12%的样本在检验的前500小时内失效。
· 预期大约20%的样本在1000小时结束时失效。
· 绝缘材料失效时间服从Weibull 分布。
2.Minitab操作
3.Minitab结果解释
Minitab 使用尺度为 6464.18、形状为 0.8037 的Weibull分布计算样本数量。
在删失时间为 1000 小时,单边置信区间的目标置信水平为 95% 的情况下,每个精度值的计算样本数量如下所示:
· 必须检验354个单元,以估计100小时内第10个百分位数的下限。
· 必须检验61个单元,以估计200小时内第10个百分位数的下限。
· 必须检验15个单元,以估计300小时内第10个百分位数的下限。
使用估计试验方案可以确定估计具有指定精度的百分位数或可靠性值所需的试验单元数。
估计试验方案可用于回答以下这类问题:
1)我应当检验多少单元才能以95%的置信下限在估计值的100小时之内估计出第 10 个百分位数?
2)工程师需要检验多少根电缆才能检验到故障,进而预测电缆在5000磅力作用下的生存概率?
既然我们知道如何估计基准可靠性,我们就需要验证我们产品的实际可靠性并加以改进。
未完待续…… 收起阅读 »
这项技术的目标包括:
1)核实(或验证)是否符合要求
2)提高对产品、过程、失效模式和机制的了解
3)识别缺陷(不足)
4)检测出需要改进设计的领域
产品的可靠性源于其子系统、组件和材料的可靠性:
系统可靠性 = f(组件可靠性)
为了实施这项技术,必须对系统及其功能、使用条件和要求具有清晰的了解。
我们可以根据现场数据(如果可靠且可追踪), 或失效物理分析方面的知识、类似产品的可靠性预测记录、模拟模型、可比子系统和组件的保修和试验数据,计算出子系统和组件的基准可靠性。为了成功完成您的基准可靠性评估,我们推荐 Minitab统计分析软件中的以下任意一种工具:
1)试验方案
2)可修复系统分析
3)寿命数据回归
4)概率分析
估计试验方案
在下面的示例中,我们说明了如何使用估计试验方案来开发一种新型的绝缘材料。
1.案例背景
工程师正在研制一种新型绝缘材料。他们要确定当与要估计的下限的距离在 100、200 和 300 小时之内时,估计第10个百分位数所需的样本数量。工程师将针对小样本执行 1000 小时的可靠性检验。他们针对检验计划使用以下信息:
· 预期大约12%的样本在检验的前500小时内失效。
· 预期大约20%的样本在1000小时结束时失效。
· 绝缘材料失效时间服从Weibull 分布。
2.Minitab操作
3.Minitab结果解释
Minitab 使用尺度为 6464.18、形状为 0.8037 的Weibull分布计算样本数量。
在删失时间为 1000 小时,单边置信区间的目标置信水平为 95% 的情况下,每个精度值的计算样本数量如下所示:
· 必须检验354个单元,以估计100小时内第10个百分位数的下限。
· 必须检验61个单元,以估计200小时内第10个百分位数的下限。
· 必须检验15个单元,以估计300小时内第10个百分位数的下限。
使用估计试验方案可以确定估计具有指定精度的百分位数或可靠性值所需的试验单元数。
估计试验方案可用于回答以下这类问题:
1)我应当检验多少单元才能以95%的置信下限在估计值的100小时之内估计出第 10 个百分位数?
2)工程师需要检验多少根电缆才能检验到故障,进而预测电缆在5000磅力作用下的生存概率?
既然我们知道如何估计基准可靠性,我们就需要验证我们产品的实际可靠性并加以改进。
未完待续…… 收起阅读 »
可靠产品设计的5项技术 02-识别和评估关键的可靠性风险
随着可靠性要求的确定,产品、材料、组件和/或制造工艺也随之改变。接下来,我们要确保识别和评估这些更新可能带来的关键风险。您可以通过验证以下任何一个关键检查点来估计可靠性风险:
1)所有功能的失效模式(硬件或软件故障、接口故障、材料退化等)。失效模式是指一个部件、(子)系统可能无法满足设计意图和客户要求的模式。
2)从先前设计中得出的保修数据
3)组件或材料变更
4)新采用的现有组件是否增加了压力和风险
5)行业专家附属材料/材料
6)有效期对于新设计而言是否是一个现实目标
7)有关材料和组件的供应商分析
8)退化估计
案例:含寿命数据的回归
为了证明其中一个检查点,我们将重点说明一位工程师如何在Minitab统计软件的帮助下评估重新设计的喷气发动机压缩机箱的可靠性。
1.案例背景
为了检验设计,工程师用一台机器向每个压缩机箱投掷一个抛射物。在抛射物撞击后,工程师每隔十二个小时就会检查压缩机,看是否故障。
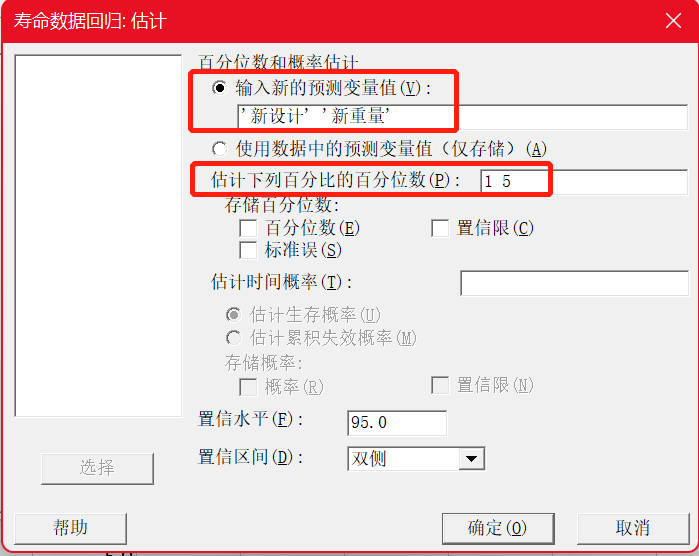
工程师执行寿命数据回归分析,以评估机箱设计、抛射物重量和失效时间之间的关系。他们还想估计他们预计的1%和5%发动机故障的失效时间。工程师使用Weibull分布对数据进行建模。
2.软件操作
对上面对话框简单说明一下:
最多输入9个变量或因子,因子既可以是数值型,也可以是文本型;
如果不说明预测变量是因子,则默认为协变量。
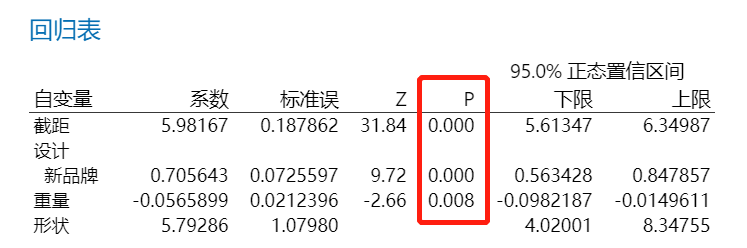
3.结果解释
在“回归表”中,设计和重量的 p 值在 α 水平 0.05 处显著。因此,工程师断定,机箱设计和抛射物重量均对失效时间造成统计意义上显著的效应。预测变量的系数可用来定义描述机箱设计、抛射物重量和发动机失效时间之间关系的方程。
下方的“百分位数表”显示每个机箱设计和抛射物重量组合的第1个和第5个百分位数。在所有抛射物重量下,与标准机箱设计相比,新机箱设计在 1% 或 5% 的发动机失效之前经过的时间更长。例如,在受到 10 磅抛射物的冲击之后,具有标准机箱设计的发动机中有 1% 预计会在大约 101.663 小时之后失效。而对于新机箱设计来说,大约有 1% 的发动机预计会在大约 205.882 小时之后失效。
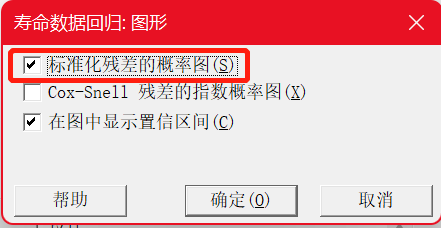
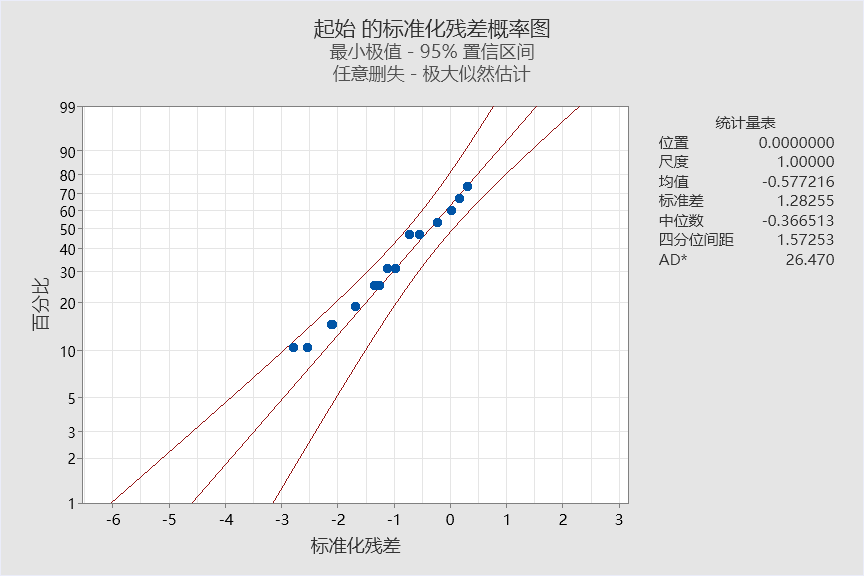
标准化残差的概率图显示,这些点近似呈一条直线。因此,可以认为该模型是合适的。
工程师可以自信地说,重新设计的喷气式发动机压缩机箱的可靠性要好于旧款。
延伸阅读
除了 Minitab统计软件外,Minitab旗下还提供另一种解决方案,可支持您的产品设计的可靠性需求。Minitab Workspace® 使您能够在一个直观界面中通过强大的可视化工具、头脑风暴图和表单来向前推进工作。
设计失效模式和影响分析 (DFMEA) 是其中一个工具,用于识别失效模式,并将产品或过程的所有要求、客户使用情况和操作条件考虑在内。输出结果包括失效物理分析(老化、可能的损害)、系统分析、可靠性预测、寿命试验和加速寿命试验和包装(存储、存储的环境条件、操作或从购买到消费的非预期用途)。
这些 Minitab 解决方案合在一起,可以有效地解决您的可靠性需求。
在评估完关键的可靠性风险后,我们要评估基准可靠性,未完待续…… 收起阅读 »
为什么化学工程师应该了解方差分析
一般来说,如果您是一名化学工程师,您可能正在开发和设计化工制造工艺。与其他工程师不同,化学工程师可能需要应用化学、生物学、物理学和数学原理来解决与化学品、燃料、药物、食品和许多其他产品的生产或使用相关的问题。因为将所有时间都用在了科学方面,如果您没有如所希望的在统计上花费足够时间,请不必担心,Minitab 随时为您服务!现在,让我们谈谈为什么方差分析 (ANOVA) 可以成为化学工程师的秘密武器。
为什么您应该了解方差分析
许多工业应用都需要进行实验,其目的是了解组之间是否存在差异。在统计方面,我们考虑一个因子(比如:催化剂类型)并且想了解该因子的各水平(比如:催化剂 1、2、 3 和 4)之间在统计意义上是否有显著差异。当各组的测量是连续的并且满足某些其他假设时,我们使用方差分析来比较各组的平均值。从某种意义上说,“方差分析”这个用词并不恰当,因为我们比较的是各组的均值。然而,通过分析组水平内和组间数据的变化,我们可以确定组均值是否在统计意义上不同。
方差分析检验总体均值(以符号 µ 表示)均相等的原假设。我们将使用样本均值来估计总体均值。如果这个原假设被否定,那么得出的结论是总体均值并不完全相等。
原假设:Ho: µCatalyst 1 = µCatalyst 2 = µCatalyst 3 = µCatalyst 4
简单地说,我们假设各组的均值相等,我们收集证据来证明这一点,即如果我们观察到这些均值之间存在较大差异,则更有可能否定此观点并假设组水平内存在差异。
单因子方差分析示例
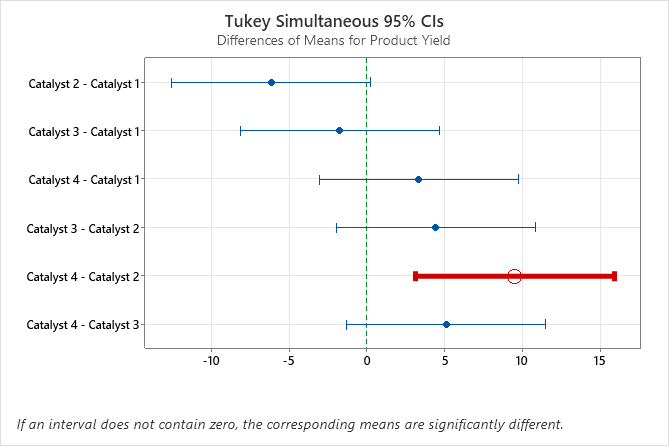
想象一下,化学工程师想要比较使用四种不同催化剂的产品产量。 她将催化剂加热与产品一起反应。使用方差分析,工程师可以确定使用不同催化剂的产品产量是否有显著差异。
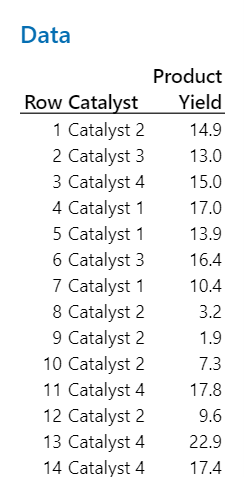
首先,工程师收集数据,如下所示。
接下来,运行单因子方差分析。
产品产量方差分析的 p 值很小,表明如果原假设成立,即催化剂均值相等,我们观察到这些结果的可能性很小。由于 p 值小于 5% 显著性水平(使用 alpha = 0.05),我们否定原假设。得出的结论是不同催化剂组的平均产品产量不同。
工程师即得知某些组的均值不同。下一个逻辑问题是哪些组的均值不同?
使用 TUKEY 法进行多重比较
虽然通过方差分析,我们知道了某些组的均值不同,但工程师需要进行更深入的比较才能了解到底哪些组的均值不同。Minitab 为此提供了“比较”功能。在我们的示例中,化学工程师使用 Tukey 比较来正式检验组对之间的差异,以了解哪些组对在统计上有显著差异。
Tukey 多重比较检验是多项检验中最保守的检验,可用于确定一组均值中的哪个均值与其他均值不同。方差分析之后使用 Tukey 法(这就是为什么您可能会听到被称为事后检验的方法),可用于为因子水平均值之间的所有成对差异创建置信区间,同时将整体误差率控制在指定的水平。
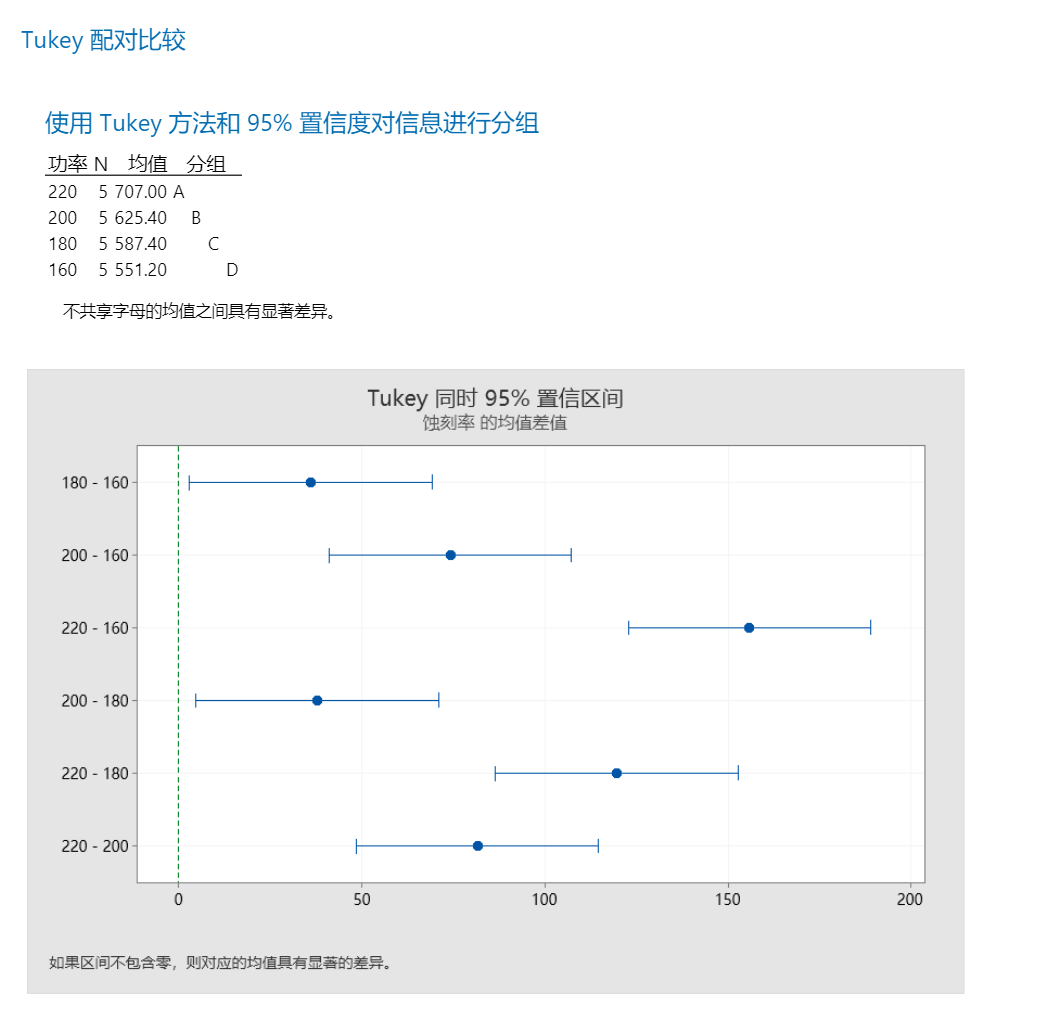
在我们的示例中,包含 Tukey 整体置信区间的图形显示催化剂 2 和 4 的均值间差异的置信区间为 3.114 到 15.886。此范围不包含零,这表明这些均值之间的差异显著。工程师可使用此差值的估计值来确定差异是否实际显著。
相反,其余均值对的置信区间均包含零,这表示差异不显著。
为什么不做一组 T 检验来判别差异?
这是个好的问题,而且经常被问到!此问题的答案与犯错的风险有关,特别是错误地认为存在统计显著差异的风险,这就是我们所说的 Alpha 风险。当我们进行一项检验时,有 5% 的机会我们会说存在差异,而实际上并没有。如果是 4 种催化剂,将进行 6 次 t 检验!
仅凭偶然的机会观察到至少一个显著性结果的概率是多少?
P(至少一个显著性结果)= 1 − P(无显著性结果)
= 1 − (1 − 0.05)6
≈ 0.264
因此,考虑到需要进行 6 次检验,我们有 26% 的机会观察到至少一个显著性结果,即使所有检验实际都不显著。事后检验控制实验误差率;更简单地说,我们希望确保错误地认为任何催化剂对存在显著性差异的机会保持在 5%。这正是 Tukey 检验为我们所做的!
答案是方差分析
使用方差分析使化学工程师能够检验混料以查看结果是否统计意义显著。同样重要的是,还可以使用比较检验确定整组是否存在差异,或者可能差异只存在于组的某部分内。在我们的示例中,只有催化剂 2 和催化剂 4 在产品产量方面在统计上有显著差异。根据这些信息,化学工程师可能会开始查看其他催化剂,以确定哪种催化剂最具成本效益、保质期最长,或最容易获得(因为知道它将产生类似数量的产品)。 收起阅读 »
为什么您应该了解方差分析
许多工业应用都需要进行实验,其目的是了解组之间是否存在差异。在统计方面,我们考虑一个因子(比如:催化剂类型)并且想了解该因子的各水平(比如:催化剂 1、2、 3 和 4)之间在统计意义上是否有显著差异。当各组的测量是连续的并且满足某些其他假设时,我们使用方差分析来比较各组的平均值。从某种意义上说,“方差分析”这个用词并不恰当,因为我们比较的是各组的均值。然而,通过分析组水平内和组间数据的变化,我们可以确定组均值是否在统计意义上不同。
方差分析检验总体均值(以符号 µ 表示)均相等的原假设。我们将使用样本均值来估计总体均值。如果这个原假设被否定,那么得出的结论是总体均值并不完全相等。
原假设:Ho: µCatalyst 1 = µCatalyst 2 = µCatalyst 3 = µCatalyst 4
简单地说,我们假设各组的均值相等,我们收集证据来证明这一点,即如果我们观察到这些均值之间存在较大差异,则更有可能否定此观点并假设组水平内存在差异。
单因子方差分析示例
想象一下,化学工程师想要比较使用四种不同催化剂的产品产量。 她将催化剂加热与产品一起反应。使用方差分析,工程师可以确定使用不同催化剂的产品产量是否有显著差异。
首先,工程师收集数据,如下所示。
接下来,运行单因子方差分析。
产品产量方差分析的 p 值很小,表明如果原假设成立,即催化剂均值相等,我们观察到这些结果的可能性很小。由于 p 值小于 5% 显著性水平(使用 alpha = 0.05),我们否定原假设。得出的结论是不同催化剂组的平均产品产量不同。
工程师即得知某些组的均值不同。下一个逻辑问题是哪些组的均值不同?
使用 TUKEY 法进行多重比较
虽然通过方差分析,我们知道了某些组的均值不同,但工程师需要进行更深入的比较才能了解到底哪些组的均值不同。Minitab 为此提供了“比较”功能。在我们的示例中,化学工程师使用 Tukey 比较来正式检验组对之间的差异,以了解哪些组对在统计上有显著差异。
Tukey 多重比较检验是多项检验中最保守的检验,可用于确定一组均值中的哪个均值与其他均值不同。方差分析之后使用 Tukey 法(这就是为什么您可能会听到被称为事后检验的方法),可用于为因子水平均值之间的所有成对差异创建置信区间,同时将整体误差率控制在指定的水平。
在我们的示例中,包含 Tukey 整体置信区间的图形显示催化剂 2 和 4 的均值间差异的置信区间为 3.114 到 15.886。此范围不包含零,这表明这些均值之间的差异显著。工程师可使用此差值的估计值来确定差异是否实际显著。
相反,其余均值对的置信区间均包含零,这表示差异不显著。
为什么不做一组 T 检验来判别差异?
这是个好的问题,而且经常被问到!此问题的答案与犯错的风险有关,特别是错误地认为存在统计显著差异的风险,这就是我们所说的 Alpha 风险。当我们进行一项检验时,有 5% 的机会我们会说存在差异,而实际上并没有。如果是 4 种催化剂,将进行 6 次 t 检验!
仅凭偶然的机会观察到至少一个显著性结果的概率是多少?
P(至少一个显著性结果)= 1 − P(无显著性结果)
= 1 − (1 − 0.05)6
≈ 0.264
因此,考虑到需要进行 6 次检验,我们有 26% 的机会观察到至少一个显著性结果,即使所有检验实际都不显著。事后检验控制实验误差率;更简单地说,我们希望确保错误地认为任何催化剂对存在显著性差异的机会保持在 5%。这正是 Tukey 检验为我们所做的!
答案是方差分析
使用方差分析使化学工程师能够检验混料以查看结果是否统计意义显著。同样重要的是,还可以使用比较检验确定整组是否存在差异,或者可能差异只存在于组的某部分内。在我们的示例中,只有催化剂 2 和催化剂 4 在产品产量方面在统计上有显著差异。根据这些信息,化学工程师可能会开始查看其他催化剂,以确定哪种催化剂最具成本效益、保质期最长,或最容易获得(因为知道它将产生类似数量的产品)。 收起阅读 »
鱼骨图解释为什么我喜欢狗
多年来我意识到一件事:和无数其他人一样,我对狗情有独钟。无论是大的、小的、胖的、瘦的、活跃的、懒懒的、毛茸茸的——我都喜欢。全世界有超过 9 亿只狗,有很多狗就在你身边,所以在这个情人节,我决定通过更深入地了解并找出我爱狗的所有原因来庆祝这个情人节。
从哪里开始呢?
我是一个视觉型的人,所以我需要一些图形且有组织性的东西才能真正深入了解这一点。因为我需要头脑风暴来列出我喜欢狗的原因,所以我意识到鱼骨图或石川图将是最好的工具之一,因为它可以列出所有原因,同时清楚地捕捉到它们之间的关联和关系以及影响。
既然工具选好了,我需要确定如何创建我的鱼骨。纸和铅笔会起作用,但很快就会变得凌乱,所以我很自然地想到我应该使用 Minitab Workspace。
一步一步来
打开 Minitab Workspace 后,我开始通过在“插入”选项下的“头脑风暴工具”部分中选择“鱼骨图”来创建我的鱼骨图。弹出一个窗口,我选择了“因果图”(在此处了解不同类型的鱼骨图)。
与任何恰当的鱼骨一样,第一步是添加,在此案例中是我对狗的喜爱。然后我开始思考(我喜爱狗的)原因,即所谓的主要原因类别,这可以帮助我对原因进行适当地分组。我最终得到了四个主类别:外表、个性、获得感和行动。
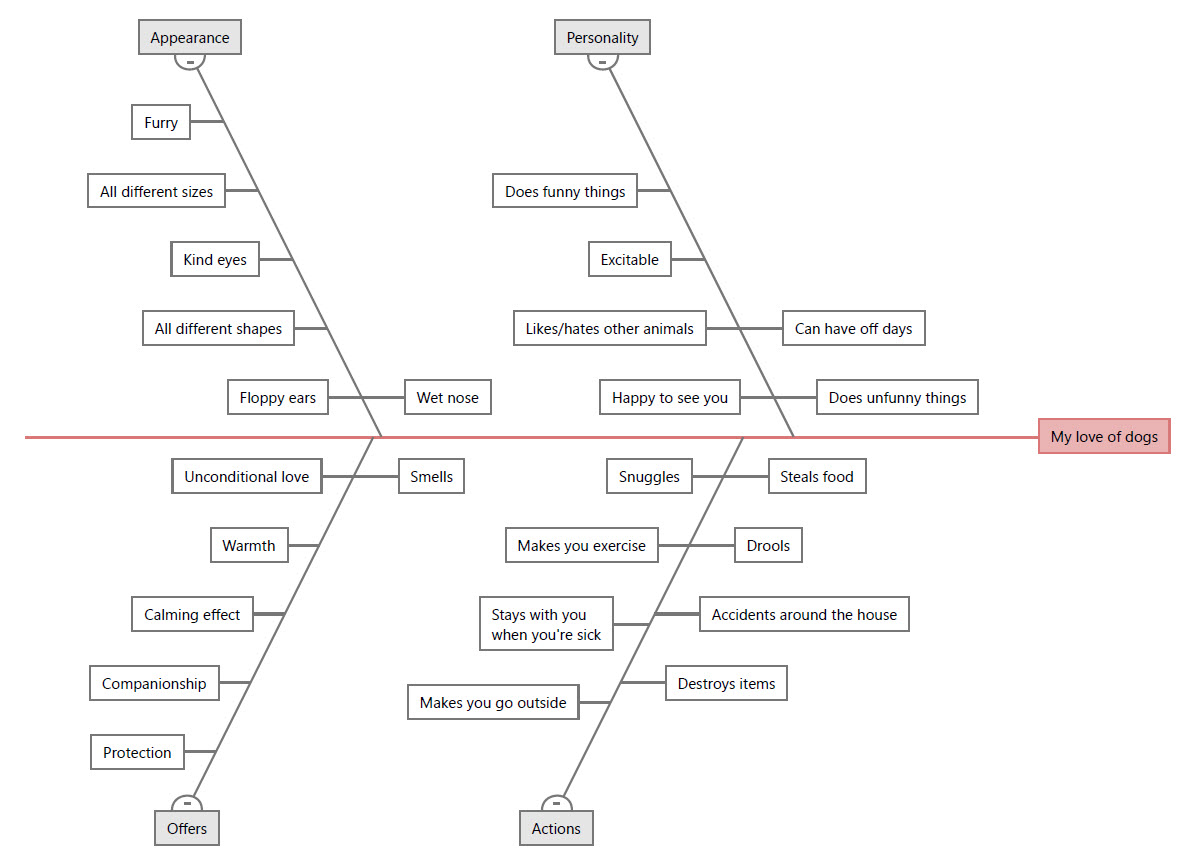
接下来,我开始“头脑风暴”,想出我爱狗的具体原因。对于每个想法,我将其分类添加到最合适的类别下。我还设置了一个计时器,确保我理智地列出最重要的原因。计时器到点后,我停下来仔细查看了我的鱼骨图。
最终结果
正如上图所示,我有26个理由说明我为什么喜欢狗。 借助 Minitab Workspace,可以轻松地在瞬间创建和可视化所有原因。
你可在鱼骨图中添加任何说明你为什么喜欢狗的内容?或者,也许您更喜欢猫!如果您想尝试创建自己的鱼骨图,请下载 Minitab Workspace 试用版。 收起阅读 »
从哪里开始呢?
我是一个视觉型的人,所以我需要一些图形且有组织性的东西才能真正深入了解这一点。因为我需要头脑风暴来列出我喜欢狗的原因,所以我意识到鱼骨图或石川图将是最好的工具之一,因为它可以列出所有原因,同时清楚地捕捉到它们之间的关联和关系以及影响。
既然工具选好了,我需要确定如何创建我的鱼骨。纸和铅笔会起作用,但很快就会变得凌乱,所以我很自然地想到我应该使用 Minitab Workspace。
一步一步来
打开 Minitab Workspace 后,我开始通过在“插入”选项下的“头脑风暴工具”部分中选择“鱼骨图”来创建我的鱼骨图。弹出一个窗口,我选择了“因果图”(在此处了解不同类型的鱼骨图)。
与任何恰当的鱼骨一样,第一步是添加,在此案例中是我对狗的喜爱。然后我开始思考(我喜爱狗的)原因,即所谓的主要原因类别,这可以帮助我对原因进行适当地分组。我最终得到了四个主类别:外表、个性、获得感和行动。
接下来,我开始“头脑风暴”,想出我爱狗的具体原因。对于每个想法,我将其分类添加到最合适的类别下。我还设置了一个计时器,确保我理智地列出最重要的原因。计时器到点后,我停下来仔细查看了我的鱼骨图。
最终结果
正如上图所示,我有26个理由说明我为什么喜欢狗。 借助 Minitab Workspace,可以轻松地在瞬间创建和可视化所有原因。
你可在鱼骨图中添加任何说明你为什么喜欢狗的内容?或者,也许您更喜欢猫!如果您想尝试创建自己的鱼骨图,请下载 Minitab Workspace 试用版。 收起阅读 »
过程能力分析01—不要忽略“稳定”
问题背景:
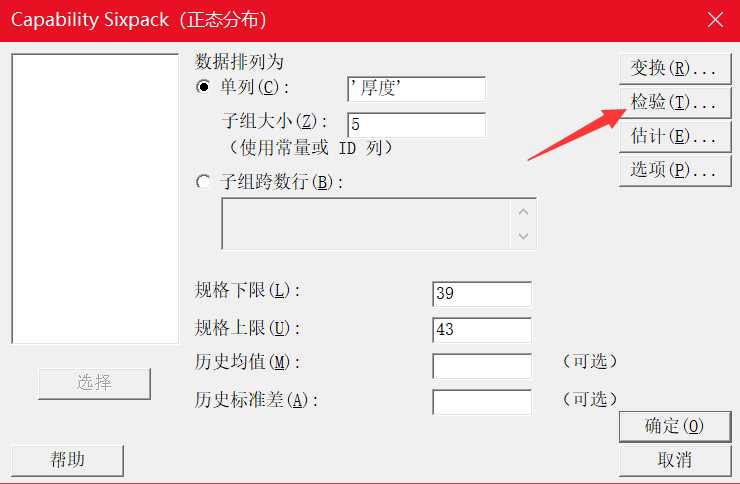
电缆制造商在电缆的外面涂上一层涂层,以保持电缆的强度和耐久性。涂层厚度的下限(LSL)为39密尔,上限(USL)为43密尔。工程师评估涂层工艺的能力,以确保它能满足客户的要求。
数据收集:
操作人员定期随机抽取5根电缆样本。这些样品充分地反映了当时工艺的内在变化。操作人员记录每根电缆样品的外涂层厚度。
Minitab操作步骤:
1.正态性检验
从上图中可以看出,正态性检验P值大于0.05,即厚度数据服从正态分布。
2.正态数据能力分析-六合一图
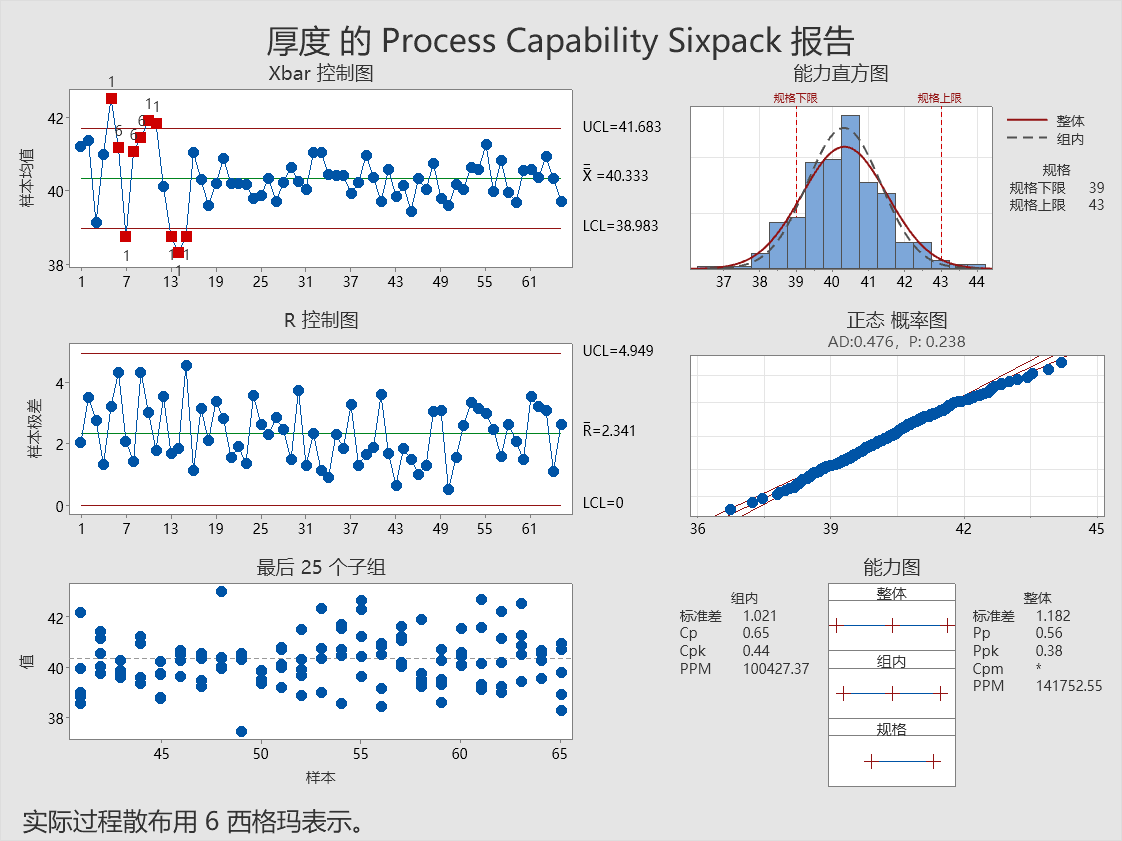
Xbar 控制图表明过程不受控制,前15个子组表现出极端的子组间变异。但是,R 控制图表明子组内极差是稳定的,因为数据都在其控制限内。
生产日志表明涂层温度的调整是造成数据早期平均厚度偏移的原因。 这些调整在子组15之后结束。控制图表明该过程在那之后是稳定的。检查子组15之后收集的数据的稳定性和正态性假设。
之前的 Capability Sixpack 分析结果发现子组 15 之后收集的数据处于控制之中。 既然这些数据是单独工作表中的子集,请使用 Capability Sixpack 评估子集数据的能力分析假设。
Xbar 和 R 控制图显示所有点都通过了特殊原因的检验并且在控制限内,这表明过程是稳定的。 因此,过程均值和标准差在研究过程中似乎是恒定的,您可以使用它们的估计来计算能力指数。
结果解释:
该过程看起来很稳定,尽管许多测量值超出了规格限制。
即使过程平均值位于规格限之间,但它也没有居中,并且大约10% 的电缆样品显示出超出这些限制的厚度值,其中大部分部件低于规格下限。
需要调整过程均值并减少变异以满足客户要求。
写在最后:
在过程能力分析之前,先做正态性检验,对于这一点我相信很多朋友已经有这个意识了,这很不错,但要注意这只是前提条件之一。其实要是想算Cp和Cpk,需要满足4个前提:数据正态、过程稳定、数据独立、MSA合格,当然如果只是想算Pp和Ppk,满足最后两个条件即可。所以说,以上分析看似没有问题,其实更好的方法是在执行过程能力分析之前去验证这些前提,包括这个案例中的“过程稳定”,不然强行算出来的Cpk也意义不大。 收起阅读 »
电缆制造商在电缆的外面涂上一层涂层,以保持电缆的强度和耐久性。涂层厚度的下限(LSL)为39密尔,上限(USL)为43密尔。工程师评估涂层工艺的能力,以确保它能满足客户的要求。
数据收集:
操作人员定期随机抽取5根电缆样本。这些样品充分地反映了当时工艺的内在变化。操作人员记录每根电缆样品的外涂层厚度。
Minitab操作步骤:
1.正态性检验
从上图中可以看出,正态性检验P值大于0.05,即厚度数据服从正态分布。
2.正态数据能力分析-六合一图
Xbar 控制图表明过程不受控制,前15个子组表现出极端的子组间变异。但是,R 控制图表明子组内极差是稳定的,因为数据都在其控制限内。
生产日志表明涂层温度的调整是造成数据早期平均厚度偏移的原因。 这些调整在子组15之后结束。控制图表明该过程在那之后是稳定的。检查子组15之后收集的数据的稳定性和正态性假设。
之前的 Capability Sixpack 分析结果发现子组 15 之后收集的数据处于控制之中。 既然这些数据是单独工作表中的子集,请使用 Capability Sixpack 评估子集数据的能力分析假设。
Xbar 和 R 控制图显示所有点都通过了特殊原因的检验并且在控制限内,这表明过程是稳定的。 因此,过程均值和标准差在研究过程中似乎是恒定的,您可以使用它们的估计来计算能力指数。
结果解释:
该过程看起来很稳定,尽管许多测量值超出了规格限制。
即使过程平均值位于规格限之间,但它也没有居中,并且大约10% 的电缆样品显示出超出这些限制的厚度值,其中大部分部件低于规格下限。
需要调整过程均值并减少变异以满足客户要求。
写在最后:
在过程能力分析之前,先做正态性检验,对于这一点我相信很多朋友已经有这个意识了,这很不错,但要注意这只是前提条件之一。其实要是想算Cp和Cpk,需要满足4个前提:数据正态、过程稳定、数据独立、MSA合格,当然如果只是想算Pp和Ppk,满足最后两个条件即可。所以说,以上分析看似没有问题,其实更好的方法是在执行过程能力分析之前去验证这些前提,包括这个案例中的“过程稳定”,不然强行算出来的Cpk也意义不大。 收起阅读 »
另辟蹊径:使用 CART 作为分析分类调查数据的替代方法
尝试了解客户/患者行为是一件很有挑战的事。研究人员往往会使用调查数据并频繁使用 Minitab 中的回归功能对其进行分析。但是,若结果变量是分类数据,而不是定量数据,则无法非常直接或直观地解释逻辑回归的结果。
有没有其他选项可用来分析 Minitab 中的调查数据?最新版 Minitab 中提供了一种解释性的、基于树的机器学习技术——CART®(分类和回归树)。探究 CART 的丰富功能!
什么是 CART?
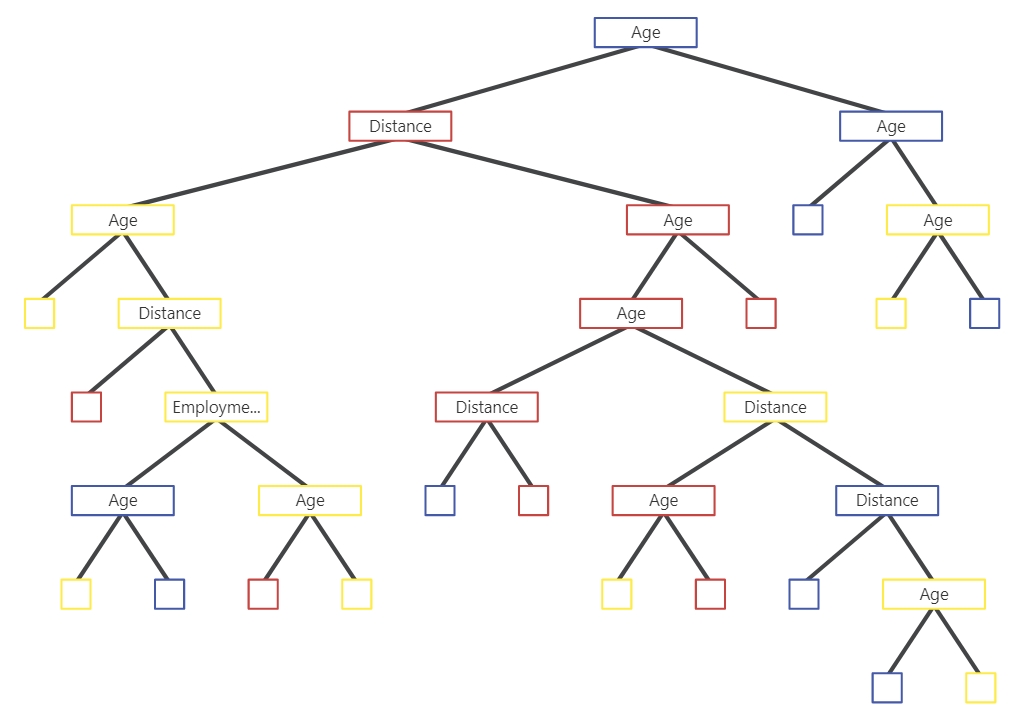
CART 是一种决策树算法,它会创建一组“是/否”规则,然后利用这些规则并基于预测变量或输入设置将目标或结果变量拆分到多个分区。产生的模型以决策树形式呈现,以展示如何基于输入设置对目标或结果变量进行分区。
Minitab 的 CART 算法可自动查找最优数目的末端节点(也称为拆分或最终分组),目的就是尽可能地提高模型的预测能力。
最出色的表现是什么?完成分析后,CART 的输出包含直观的可视解释,因此,您不必是数据科学家,也能从数据中收获极有价值的见解。
(图像下层:注意:默认情况下,Minitab 会显示具体的 CART 树。右键单击树并选择结点拆分视图,可查看上层简要视图。)
借助 CART 充分发挥免预约诊所数据的作用
了解 CART 是什么之后,接下来我们看下它的工作原理。
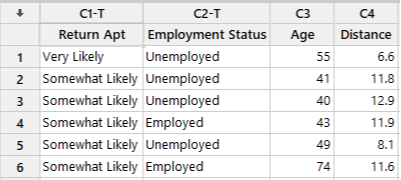
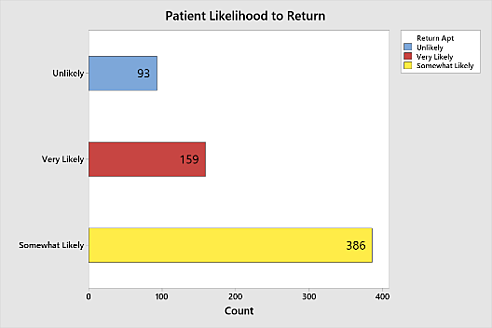
连锁免预约诊所收集患者的调查数据,询问了他们未来有多大可能性会再次光顾诊所:极有可能、有可能或不可能。诊所员工还会记录患者的年龄、从家里到诊所的距离(以英里为单位)以及就业状态。诊所的地区经理尤其关注到底是什么因素在影响无预约患者再次来诊所接受服务的意愿。
如图显示数据子集,还有一个条形图展示了诊所无预约患者给出的响应。
我们可以使用 CART 来预测分类结果的似然性,在这个案例中,指的就是患者再次光顾诊所的可能性。Minitab 的 CART 分类引擎提供的直观界面可以处理二元结果(两组)或多项式结果(至少三组)。
经理将她的数据输入 Minitab 后,选择统计 > 预测分析 > CART® 分类,界面上随后显示了以下内容:
由于存在至少三组,因此她先选择多项式响应,然后在响应中选择“再次光顾的意向”,这也是她想预测的目标。接着,依次快速输入连续预测变量和分类预测变量或者要用来进行预测的其他输入,填写好对话框。
CART 会自动处理缺失值,而且对极端异常值不敏感,也不会假定存在要检查的分布、p 值或残差。因此,CART 十分简单易用,即便是初学者也能快速上手。此外,Minitab 的 CART 功能会仔细、谨慎地将数据分区为两组:一部分数据用于构建模型(学习数据),而另一部分数据则用于评估模型执行新预测的能力(测试数据)。
针对每一个目标变量对,CART 分析的输出会显示大于或等于 0.93 的 (ROC) 曲线下的面积值。ROC 可以帮助经理将模型预测患者再次光顾诊所的意愿的准确性进行可视化。该图显示了敏感性(正确预测为正类的正类)与特异性(正确预测为负类的负类)之间的关系。
这个模型能够如此准确地预测患者未来再次光顾诊所的意愿,经理感到非常满意。
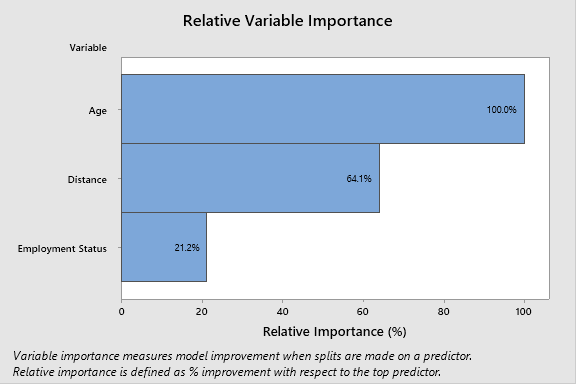
经理之前认为,患者与诊所之间的距离是影响此人再次光顾诊所的意愿的最佳预测变量。但令她吃惊的是,结果并非如此。在 CART 的相对变量重要性图中,清晰显示了每一个预测变量对于决定患者是否再次光顾诊所的对应重要性。
最终结果
快速评估上方变量重要性图后发现,患者的年龄才是影响他们是否会再次光顾诊所的意愿的最佳预测变量,距离的影响程度紧随其后,而就业状态的重要性最低。
通过深入了解患者行为,将有助于地区经理创建再次光顾诊所可能性高的客户的个人资料,这样诊所中心也就能有针对性地发送额外宣传单和推出激励措施,从而确保这些客户再次光顾。例如,不满 43 岁而且与诊所距离不到 11 英里的患者,无论就业状态如何,都极有可能再次光顾。年龄介于 71 到 82 岁之间的患者,无论距离或就业状态如何,都有可能再次光顾。相比之下,年龄介于 67 到 71 岁之间的那些患者,若与诊所的距离超过 11 英里,无论其他因素如何,他们都不大可能再次光顾。
收起阅读 »
迎难而上:向投身数学与统计学的女性致敬
每年三月,对于美国的女性来说都是具有历史意义的月份。我们纪念那些具有开拓精神、坚韧不拔且拥有巨大影响力的女性并向其致以崇高敬意。当全世界都在应对疫情时,毫无疑问,情况与往年相比有很大不同。
本着这种精神,我们花了一些时间展示我们这个领域众多女性中的几位代表人物,她们迎难而上并做出了突出贡献。
弗洛伦斯·南丁格尔用数据可视化的方式说明
卫生和洗手的道理
您可能知道被称为“掌灯女士”和现代护理学奠基人的弗洛伦斯·南丁格尔,然而,您知道她还是一位著名的统计学家吗?
南丁格尔始终认为自己受到召唤要去护理和帮助他人。经过在法国和德国学习并担任伦敦病弱淑女收容所所长后,在克里米亚战争期间,她在土耳其的一家英国医院帮忙,真正开始崭露头角。南丁格尔注意到这家医院存在的许多问题并加以妥善处理,包括改进医院卫生和患者护理,以及确保提供充足的医疗用品。在 1856 年离开土耳其之前,她和她的团队帮助大幅降低了死亡率并改善了医院卫生情况。
现在声名鹊起的南丁格尔在回到伦敦之后就开始着手分享她所学到的知识,说明如何通过改善卫生条件、洗手和卫生设施来挽救生命。为证明她的观点,南丁格尔收集并分析了医疗数据并在一项广泛研究中以图片形式展示,清楚表明导致战时死亡的主要原因是缺乏卫生设施,而非缺医少药或食物不足。
特别是她的数据分析显示,英国士兵的病死率是作战中阵亡率的 10 倍,由于军队医疗服务的不足,英国士兵的死亡率是平民的两倍。南丁格尔的工作使她成为英国皇家统计学会录取的第一位女性,并由此开展卫生健康政策改革,不仅拯救了无数英国士兵的生命,而且直到今天还在继续帮助拯救生命和确保人们的健康。
“人类计算机”凯瑟琳·约翰逊
帮助男人登陆月球
您看过 2016 年获奖影片“隐藏人物”吗?这部电影大致是根据凯瑟琳·约翰逊和其他黑人女数学家在太空竞赛时代在 NASA(美国国家航空航天局)工作的故事改编的。
从少年时代起,约翰逊就一直数数并表现出对数字强烈的兴趣和极高的天赋。她在学校学习飞快,进入西佛吉尼亚州立学院时甚至只有 15 岁,她的一位教授慧眼识珠,认为她是一名研究型的数学家。
约翰逊成为了一名大学教授,直至机会之门向她敞开怀抱:NACA(美国国家航空咨询委员会,即 NASA 前身)雇佣了黑人女性“计算员”检查工程师的计算结果。约翰逊也被录用,但很快从其他人中脱颖而出,因为她的好奇心很强,总是不断提问以了解“为什么”。
当肯尼迪总统提出由美国派人登月时,约翰逊加入了这个团队并于 1961 年计算出美国首次太空之旅的轨迹。最终,约翰逊继续负责 1969 年首次实际登月的计算工作。约翰逊的坚韧不拔和乐于探索的性格不仅为她打开了机会之门,更为其他妇女和女孩打开了眼界,让她们知道,追星逐梦并非遥不可及。
“统计学界的第一夫人”格特鲁德·考克斯
视统计人员为科学合作伙伴
格特鲁德·考克斯是一位美国统计学家,她于 1941 年创办了北卡罗莱纳州立大学的第一个试验统计系,这为她赢得了“统计学界的第一夫人”这一影响力巨大的头衔。
后来,她被任命为北卡罗来纳州综合大学统计研究所和北卡罗来纳州立大学统计研究部的主任。
考克斯的研究主要涉及试验设计。1934 年她在爱荷华州立大学讲授试验设计课程,但她的设计资料直到 1950 年才正式出版,当时她正与 W. G. 科克伦合作撰写《试验设计》,该书随后成为最具影响力的统计学书籍之一,直到今天仍在印刷。
1949 年,考克斯继续打破常规并成为第一位入选国际统计研究所的女性成员。1956 年,她当选为美国统计学会的主席。当被问及职业机会时,考克斯会答到“女性在统计学领域当然可以大放异彩。”由于考克斯的热情和影响力,其他妇女和女孩得以追随她的脚步以满腔热情投入统计学领域。
政府经济学家珍尼特·诺伍德
铺就未来女性领导人之路
珍尼特·诺伍德是吉米·卡特于 1979 年任命的美国劳工统计局第一位女性专员,然后罗纳德·里根在八十年代又两次重新任命了她。她常常意识到自己是政府机构和专业协会会议中唯一的女性,因此她帮助人们关注、接受并认可女性的存在和领导力。
诺伍德最初在美国劳工统计局担任兼职初级经济师,但随着时间推移,她职位一路上升直至获得任命。在诺伍德的整个职业生涯中,她凭借正直、专业和公平而为人所知。她的贡献主要集中在政府统计方面,包括失业率和消费者价格指数。
在 1989 年,她追随格特鲁德·考克斯的脚步并当选为美国统计学会主席。她还在国际统计研究所和城市研究所以及其他多家专业协会担任职务。诺伍德是众多未来女性领导者的先行者。
衷心感谢上述所有女性以及过去、现在和未来为我以及其他女性奉献自我并创造机遇的全世界所有女性。 收起阅读 »
本着这种精神,我们花了一些时间展示我们这个领域众多女性中的几位代表人物,她们迎难而上并做出了突出贡献。
弗洛伦斯·南丁格尔用数据可视化的方式说明
卫生和洗手的道理
您可能知道被称为“掌灯女士”和现代护理学奠基人的弗洛伦斯·南丁格尔,然而,您知道她还是一位著名的统计学家吗?
南丁格尔始终认为自己受到召唤要去护理和帮助他人。经过在法国和德国学习并担任伦敦病弱淑女收容所所长后,在克里米亚战争期间,她在土耳其的一家英国医院帮忙,真正开始崭露头角。南丁格尔注意到这家医院存在的许多问题并加以妥善处理,包括改进医院卫生和患者护理,以及确保提供充足的医疗用品。在 1856 年离开土耳其之前,她和她的团队帮助大幅降低了死亡率并改善了医院卫生情况。
现在声名鹊起的南丁格尔在回到伦敦之后就开始着手分享她所学到的知识,说明如何通过改善卫生条件、洗手和卫生设施来挽救生命。为证明她的观点,南丁格尔收集并分析了医疗数据并在一项广泛研究中以图片形式展示,清楚表明导致战时死亡的主要原因是缺乏卫生设施,而非缺医少药或食物不足。
特别是她的数据分析显示,英国士兵的病死率是作战中阵亡率的 10 倍,由于军队医疗服务的不足,英国士兵的死亡率是平民的两倍。南丁格尔的工作使她成为英国皇家统计学会录取的第一位女性,并由此开展卫生健康政策改革,不仅拯救了无数英国士兵的生命,而且直到今天还在继续帮助拯救生命和确保人们的健康。
“人类计算机”凯瑟琳·约翰逊
帮助男人登陆月球
您看过 2016 年获奖影片“隐藏人物”吗?这部电影大致是根据凯瑟琳·约翰逊和其他黑人女数学家在太空竞赛时代在 NASA(美国国家航空航天局)工作的故事改编的。
从少年时代起,约翰逊就一直数数并表现出对数字强烈的兴趣和极高的天赋。她在学校学习飞快,进入西佛吉尼亚州立学院时甚至只有 15 岁,她的一位教授慧眼识珠,认为她是一名研究型的数学家。
约翰逊成为了一名大学教授,直至机会之门向她敞开怀抱:NACA(美国国家航空咨询委员会,即 NASA 前身)雇佣了黑人女性“计算员”检查工程师的计算结果。约翰逊也被录用,但很快从其他人中脱颖而出,因为她的好奇心很强,总是不断提问以了解“为什么”。
当肯尼迪总统提出由美国派人登月时,约翰逊加入了这个团队并于 1961 年计算出美国首次太空之旅的轨迹。最终,约翰逊继续负责 1969 年首次实际登月的计算工作。约翰逊的坚韧不拔和乐于探索的性格不仅为她打开了机会之门,更为其他妇女和女孩打开了眼界,让她们知道,追星逐梦并非遥不可及。
“统计学界的第一夫人”格特鲁德·考克斯
视统计人员为科学合作伙伴
格特鲁德·考克斯是一位美国统计学家,她于 1941 年创办了北卡罗莱纳州立大学的第一个试验统计系,这为她赢得了“统计学界的第一夫人”这一影响力巨大的头衔。
后来,她被任命为北卡罗来纳州综合大学统计研究所和北卡罗来纳州立大学统计研究部的主任。
考克斯的研究主要涉及试验设计。1934 年她在爱荷华州立大学讲授试验设计课程,但她的设计资料直到 1950 年才正式出版,当时她正与 W. G. 科克伦合作撰写《试验设计》,该书随后成为最具影响力的统计学书籍之一,直到今天仍在印刷。
1949 年,考克斯继续打破常规并成为第一位入选国际统计研究所的女性成员。1956 年,她当选为美国统计学会的主席。当被问及职业机会时,考克斯会答到“女性在统计学领域当然可以大放异彩。”由于考克斯的热情和影响力,其他妇女和女孩得以追随她的脚步以满腔热情投入统计学领域。
政府经济学家珍尼特·诺伍德
铺就未来女性领导人之路
珍尼特·诺伍德是吉米·卡特于 1979 年任命的美国劳工统计局第一位女性专员,然后罗纳德·里根在八十年代又两次重新任命了她。她常常意识到自己是政府机构和专业协会会议中唯一的女性,因此她帮助人们关注、接受并认可女性的存在和领导力。
诺伍德最初在美国劳工统计局担任兼职初级经济师,但随着时间推移,她职位一路上升直至获得任命。在诺伍德的整个职业生涯中,她凭借正直、专业和公平而为人所知。她的贡献主要集中在政府统计方面,包括失业率和消费者价格指数。
在 1989 年,她追随格特鲁德·考克斯的脚步并当选为美国统计学会主席。她还在国际统计研究所和城市研究所以及其他多家专业协会担任职务。诺伍德是众多未来女性领导者的先行者。
衷心感谢上述所有女性以及过去、现在和未来为我以及其他女性奉献自我并创造机遇的全世界所有女性。 收起阅读 »
1分钟教你制作交互作用图
夹板是通过圆木沿轴旋转时切削成的薄木片制成的。需要施以相当大的力旋转硬圆木,才能使锋利的刀片切下薄木片。将夹具插入圆木的两端,以便施加必要的扭矩旋转圆木。您进行了一项试验研究影响扭矩的因子。这些因子包括圆木的直径、夹具插入深度以及圆木的温度。您想预览数据以检查是否存在交互作用。
直径 插入深度 温度 扭矩
4.5 1 60 17.3
4.5 1.5 60 18.05
4.5 2.25 60 17.4
4.5 3.25 60 17.4
4.5 1 120 16.7
4.5 1.5 120 17.95
4.5 2.25 120 18.6
4.5 3.25 120 18.55
4.5 1 150 15.75
4.5 1.5 150 16.65
4.5 2.25 150 15.25
4.5 3.25 150 15.85
7.5 1 60 29.55
7.5 1.5 60 31.5
7.5 2.25 60 36.75
7.5 3.25 60 41.2
7.5 1 120 23.2
7.5 1.5 120 25.9
7.5 2.25 120 35.65
7.5 3.25 120 37.6
7.5 1 150 22.55
7.5 1.5 150 22.9
7.5 2.25 150 28.9
7.5 3.25 150 35.2
操作: 6SQ统计--方差分析—交互作用图

响应数据范围,选择 扭矩列
因子数据范围,选择 直径和插入深度,温度列
输出结果
解释结果
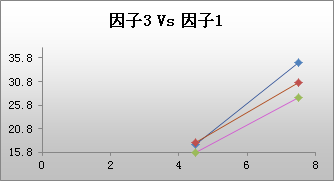
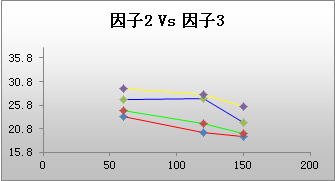
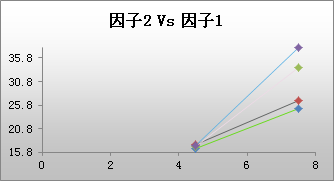
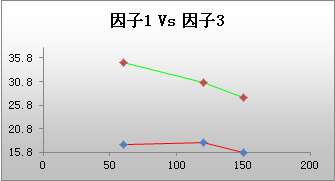
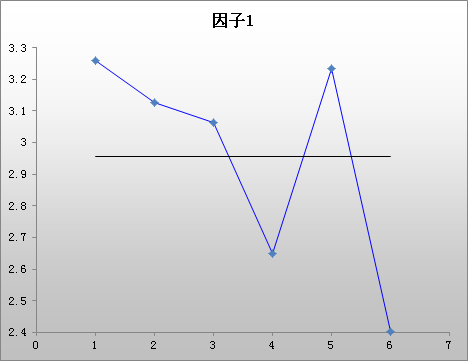
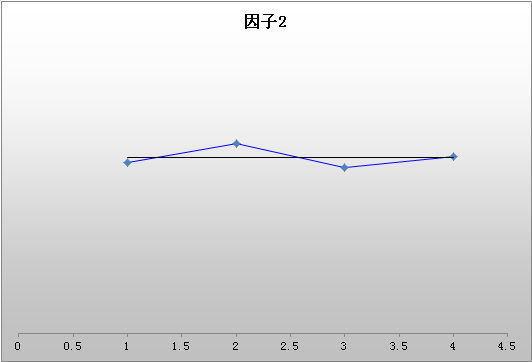
三因子或多因子交互作用图为所有双因子组合分别显示一个双因子交互作用图。在本示例中,顶行中间的图显示了两个直径水平(4.5 和 7.5)下相对于渗透力水平的平均扭矩,而且在所有温度水平上进行了平均。对于直径*温度(右上方)和渗透力*温度(第二行),也存在类似的交互作用图。
对于本示例来说,直径*渗透力和直径*温度图显示了不平行的线,这表示交互作用。渗透力*温度交互作用是否存在难以判断。此交互作用最好是结合模型拟合过程(例如,一般线性模型)来判断。
Excel数据案例:
http://pan.baidu.com/s/1i5AXSRN
6SQ统计3.0企业版90天试用下载 http://pan.baidu.com/s/1i5AXSRN
收起阅读 »
直径 插入深度 温度 扭矩
4.5 1 60 17.3
4.5 1.5 60 18.05
4.5 2.25 60 17.4
4.5 3.25 60 17.4
4.5 1 120 16.7
4.5 1.5 120 17.95
4.5 2.25 120 18.6
4.5 3.25 120 18.55
4.5 1 150 15.75
4.5 1.5 150 16.65
4.5 2.25 150 15.25
4.5 3.25 150 15.85
7.5 1 60 29.55
7.5 1.5 60 31.5
7.5 2.25 60 36.75
7.5 3.25 60 41.2
7.5 1 120 23.2
7.5 1.5 120 25.9
7.5 2.25 120 35.65
7.5 3.25 120 37.6
7.5 1 150 22.55
7.5 1.5 150 22.9
7.5 2.25 150 28.9
7.5 3.25 150 35.2
操作: 6SQ统计--方差分析—交互作用图

响应数据范围,选择 扭矩列
因子数据范围,选择 直径和插入深度,温度列
输出结果
解释结果
三因子或多因子交互作用图为所有双因子组合分别显示一个双因子交互作用图。在本示例中,顶行中间的图显示了两个直径水平(4.5 和 7.5)下相对于渗透力水平的平均扭矩,而且在所有温度水平上进行了平均。对于直径*温度(右上方)和渗透力*温度(第二行),也存在类似的交互作用图。
对于本示例来说,直径*渗透力和直径*温度图显示了不平行的线,这表示交互作用。渗透力*温度交互作用是否存在难以判断。此交互作用最好是结合模型拟合过程(例如,一般线性模型)来判断。
Excel数据案例:
http://pan.baidu.com/s/1i5AXSRN
6SQ统计3.0企业版90天试用下载 http://pan.baidu.com/s/1i5AXSRN
收起阅读 »
1分钟教你制作主效应图
您在四片地里分块种植了六种不同的紫花苜蓿,并对收割的产量进行了称量。您想比较不同品种的产量,并将田地视为区组。您想使用主效应图来预览数据,并按品种和田地检查产量。
数据:
产出 品种 现场
3.22 1 1
3.04 2 1
3.06 3 1
2.64 4 1
3.19 5 1
2.49 6 1
3.31 1 2
2.99 2 2
3.17 3 2
2.75 4 2
3.4 5 2
2.37 6 2
3.26 1 3
3.27 2 3
2.93 3 3
2.59 4 3
3.11 5 3
2.38 6 3
3.25 1 4
3.2 2 4
3.09 3 4
2.62 4 4
3.23 5 4
2.37 6 4
操作: 6SQ统计--方差分析—主效应图
响应数据范围,选择 产出列
因子数据范围,选择 品种和现场列
点击确定,输出结果
、
解释结果
除非已指定值顺序,否则对于数字或日期/时间,主效应图将按排序顺序显示每个因子水平 的响应平均值,对于文本,则按字母顺序显示响应平均值(请参见确定文本类别的顺序)。同时在总平均值处绘制一条水平线。效应就是平均值与参考线之间的差。在本示例中,与田地(区组变量)的效应相比,品种对产量的效应很大。
Excel数据案例:
http://pan.baidu.com/s/1i5AXSRN
6SQ统计3.0企业版90天试用下载 http://pan.baidu.com/s/1i5AXSRN
收起阅读 »
数据:
产出 品种 现场
3.22 1 1
3.04 2 1
3.06 3 1
2.64 4 1
3.19 5 1
2.49 6 1
3.31 1 2
2.99 2 2
3.17 3 2
2.75 4 2
3.4 5 2
2.37 6 2
3.26 1 3
3.27 2 3
2.93 3 3
2.59 4 3
3.11 5 3
2.38 6 3
3.25 1 4
3.2 2 4
3.09 3 4
2.62 4 4
3.23 5 4
2.37 6 4
操作: 6SQ统计--方差分析—主效应图
响应数据范围,选择 产出列
因子数据范围,选择 品种和现场列
点击确定,输出结果
、
解释结果
除非已指定值顺序,否则对于数字或日期/时间,主效应图将按排序顺序显示每个因子水平 的响应平均值,对于文本,则按字母顺序显示响应平均值(请参见确定文本类别的顺序)。同时在总平均值处绘制一条水平线。效应就是平均值与参考线之间的差。在本示例中,与田地(区组变量)的效应相比,品种对产量的效应很大。
Excel数据案例:
http://pan.baidu.com/s/1i5AXSRN
6SQ统计3.0企业版90天试用下载 http://pan.baidu.com/s/1i5AXSRN
收起阅读 »
1分钟教你制作过程能力分析(Poisson)
假设您为一家电线制造商工作,并关注电线绝缘过程的有效性。您随机抽取不同长度的电线,并通过对其施加测试电压来检验是否有绝缘薄弱的点。您记录弱点数和每段电线的长度(以英尺计)。
弱点 长度
2 132
4 130
3 120
1 124
2 138
5 148
2 101
5 102
4 124
1 119
6 120
3 123
3 101
6 121
1 133
4 138
1 113
8 119
1 128
4 103
4 140
2 150
4 121
2 140
1 114
2 140
2 136
3 114
4 149
4 110
1 100
0 138
4 118
6 116
5 131
11 146
1 147
4 142
2 140
4 142
2 136
2 139
3 147
5 122
1 149
1 142
2 116
2 146
5 140
3 129
3 100
6 124
5 141
8 130
5 102
2 110
4 134
4 145
3 110
3 105
4 148
3 144
4 100
2 102
6 142
4 105
2 133
5 129
3 108
4 103
2 132
2 108
4 111
7 107
5 108
1 102
7 111
2 102
2 137
0 128
1 120
5 124
2 100
2 135
4 148
6 103
3 127
3 104
4 106
3 113
2 124
3 100
3 116
1 140
5 135
4 126
3 116
2 103
1 136
2 132
1, 6SQ统计--质量工具--能力分析(Poisson)
2 ,选择缺陷数和子组大小数据列
点击确认,输出结果
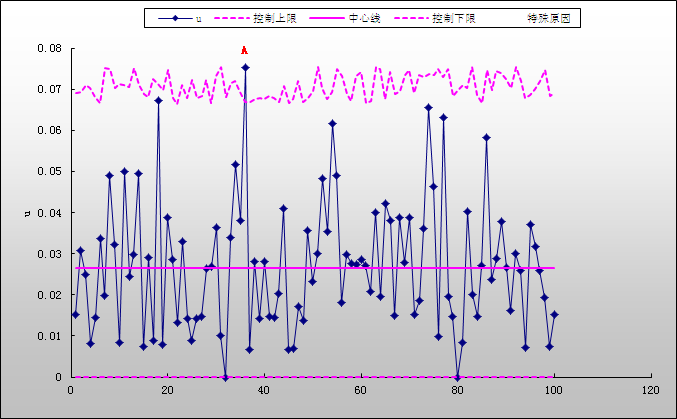
输出结果
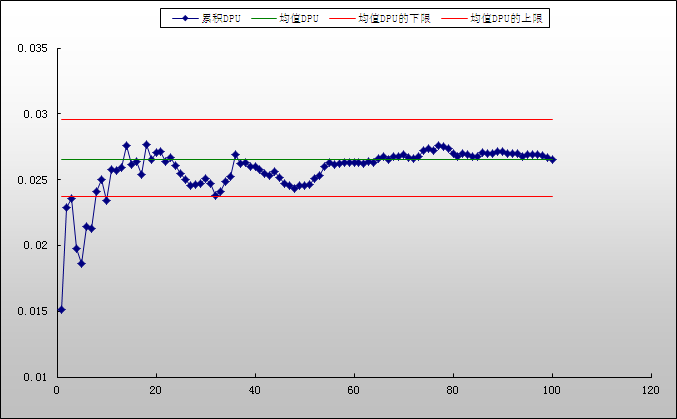
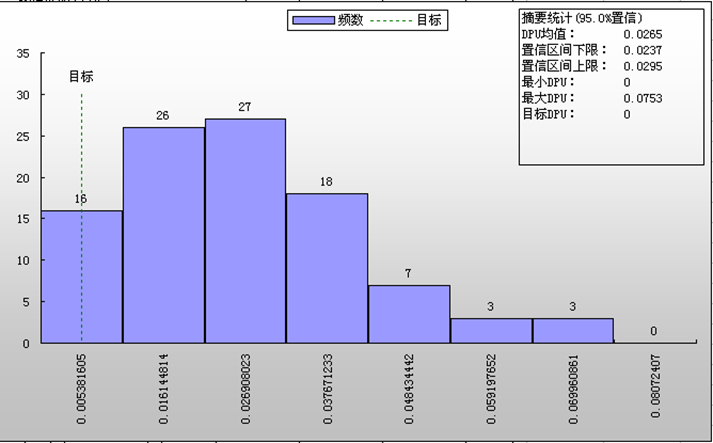
累积 DPU 控制图 (每单位的缺陷数 )停留在值 0.0265 附近,表明收集的样本足以很好地估计 DPU 均值。DPU 的比率似乎不受电线长度的影响。
Excel数据案例:
http://pan.baidu.com/s/1i5AXSRN
6SQ统计3.0企业版90天试用下载 http://pan.baidu.com/s/1i5AXSRN
收起阅读 »
弱点 长度
2 132
4 130
3 120
1 124
2 138
5 148
2 101
5 102
4 124
1 119
6 120
3 123
3 101
6 121
1 133
4 138
1 113
8 119
1 128
4 103
4 140
2 150
4 121
2 140
1 114
2 140
2 136
3 114
4 149
4 110
1 100
0 138
4 118
6 116
5 131
11 146
1 147
4 142
2 140
4 142
2 136
2 139
3 147
5 122
1 149
1 142
2 116
2 146
5 140
3 129
3 100
6 124
5 141
8 130
5 102
2 110
4 134
4 145
3 110
3 105
4 148
3 144
4 100
2 102
6 142
4 105
2 133
5 129
3 108
4 103
2 132
2 108
4 111
7 107
5 108
1 102
7 111
2 102
2 137
0 128
1 120
5 124
2 100
2 135
4 148
6 103
3 127
3 104
4 106
3 113
2 124
3 100
3 116
1 140
5 135
4 126
3 116
2 103
1 136
2 132
1, 6SQ统计--质量工具--能力分析(Poisson)

2 ,选择缺陷数和子组大小数据列
点击确认,输出结果
输出结果
累积 DPU 控制图 (每单位的缺陷数 )停留在值 0.0265 附近,表明收集的样本足以很好地估计 DPU 均值。DPU 的比率似乎不受电线长度的影响。
Excel数据案例:
http://pan.baidu.com/s/1i5AXSRN
6SQ统计3.0企业版90天试用下载 http://pan.baidu.com/s/1i5AXSRN
收起阅读 »
1分钟教你制作过程能力分析(二项)
设想你负责评估销售部门来电的回应情况,即,客户电话回应率的能力如何
通过销售代表记录下20天内每天未回应的电话(缺陷),你也要记录接入电话的总次数
目的:作出过程能力的改善基准.
数据如下:
不可用 来电数
432 1908
392 1912
497 1934
459 1889
433 1922
424 1964
470 1944
455 1919
427 1938
424 1854
410 1937
386 1838
496 2025
424 1888
425 1894
428 1941
392 1868
460 1894
425 1933
405 1862
1, 6SQ统计--质量工具--能力分析(二项)
2 ,选择缺陷数和子组大小数据列
点击确认,输出结果
输出结果
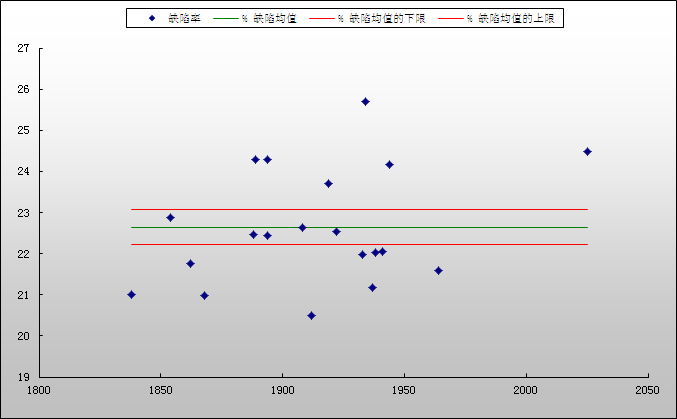
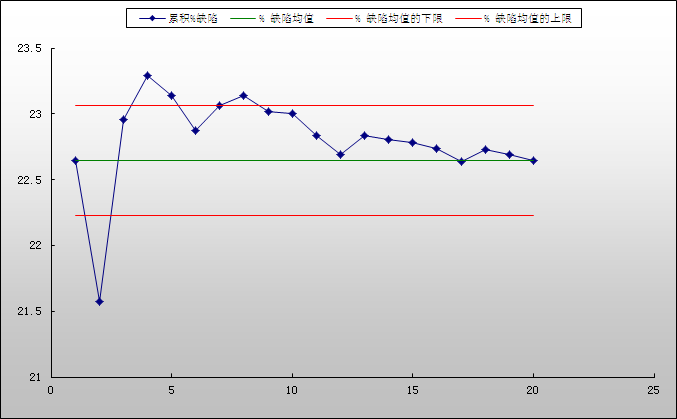
•累积%缺陷率图是百分缺陷的移动平均
•它检验你已从足够的样品中收集数据,以获得一稳定的缺陷估计数
•比率稳定在22% 左右
Excel数据案例:
http://pan.baidu.com/s/1i5AXSRN
6SQ统计3.0企业版90天试用下载 http://pan.baidu.com/s/1i5AXSRN 收起阅读 »
通过销售代表记录下20天内每天未回应的电话(缺陷),你也要记录接入电话的总次数
目的:作出过程能力的改善基准.
数据如下:
不可用 来电数
432 1908
392 1912
497 1934
459 1889
433 1922
424 1964
470 1944
455 1919
427 1938
424 1854
410 1937
386 1838
496 2025
424 1888
425 1894
428 1941
392 1868
460 1894
425 1933
405 1862
1, 6SQ统计--质量工具--能力分析(二项)
2 ,选择缺陷数和子组大小数据列
点击确认,输出结果
输出结果
•累积%缺陷率图是百分缺陷的移动平均
•它检验你已从足够的样品中收集数据,以获得一稳定的缺陷估计数
•比率稳定在22% 左右
Excel数据案例:
http://pan.baidu.com/s/1i5AXSRN
6SQ统计3.0企业版90天试用下载 http://pan.baidu.com/s/1i5AXSRN 收起阅读 »
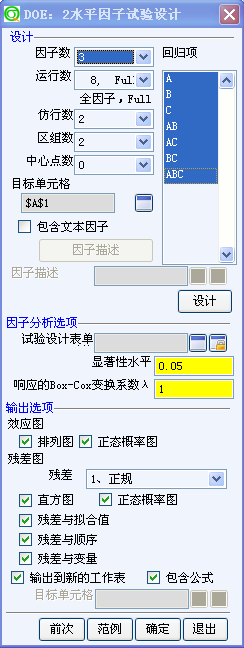
1分钟教你制作2水平因子实验设计
您是一名工程师,负责调查加工条件如何影响化学反应的产量。您认为三个加工条件(因子)- 反应时间、反应温度和催化剂类型 - 会影响产量。您有足够的资源进行 16 次化学反应试验,但一天只能进行 8 次化学反应试验。因此,您创建了一个具有两个仿行和两个区组的全因子设计。
操作: 6SQ统计>实验设计>2水平因子设计
设计实验-3因子 2仿行 2区组
1.生成实验表单
2,实验完成后,输入对应的数据
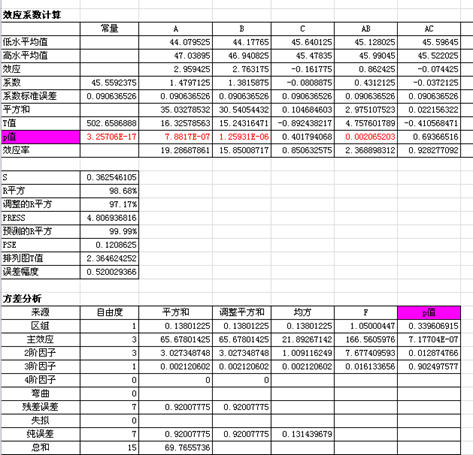
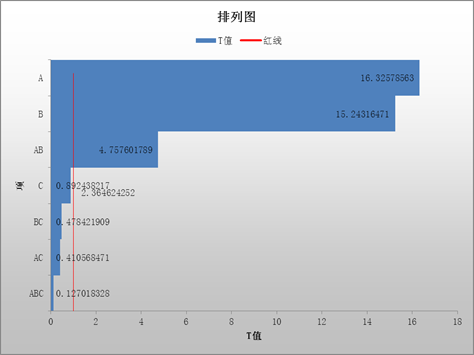
选择红框中所有数据,点击确认分析数据
P值显示主效应双因子交互作用 存在显著效应
时间温度,及时间与温度的交互作用 存在显著效应
Excel数据案例:
http://pan.baidu.com/s/1i5AXSRN
6SQ统计3.0企业版90天试用下载 http://pan.baidu.com/s/1i5AXSRN
收起阅读 »
操作: 6SQ统计>实验设计>2水平因子设计
设计实验-3因子 2仿行 2区组
1.生成实验表单
2,实验完成后,输入对应的数据
选择红框中所有数据,点击确认分析数据
P值显示主效应双因子交互作用 存在显著效应
时间温度,及时间与温度的交互作用 存在显著效应
Excel数据案例:
http://pan.baidu.com/s/1i5AXSRN
6SQ统计3.0企业版90天试用下载 http://pan.baidu.com/s/1i5AXSRN
收起阅读 »
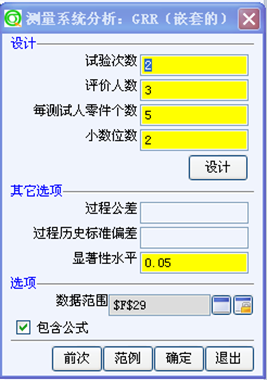
1分钟教你制作量具R&R(嵌套的)
适用于破坏性测试,每一个操作者针对的物料都是唯一的,所以不存在operator by part的交互作用
有三个操作员,每人量测5个不同的料件,每个料件测量两次,所以共有30个测量值,。每个料件对操作者都是唯一的,没有任一个料件会同时被两个操作者测量。因此我们选用量具R&R(嵌套的)方法来进行分析
1, 6SQ统计--测量系统分析--量具R&R(嵌套的)
试验次数 2
评价人3
每测试人零件个数 5
点击设计
生成表格,并填入实验数据:
过程公差是10,数据范围选择全部的红色的框内,点击确认 输出分析结果。
解释结果
查看“合计量具 R&R”和“部件之间”的“%贡献”列。部件之间差异的百分比贡献(部件之间 = 17.54)比测量系统变异的百分比贡献(合计量具 R&R = 82.46)小很多。“%研究变异”列表明“合计量具 R&R”占研究变异的 90.81%。因此,大多数变异是由于测量系统错误所致;非常少的一部分变异是由于部件之间的差异所致。请参见测量系统可接受性准则。
可区分类别数为 1 表示测量系统无法区分部件。请参见可区分类别数声明。
查看变异分量图 - 位于左上角。大多数变异是由于测量系统错误(量具 R&R)所致;非常少的一部分变异是由于部件之间的差异所致。
查看 X 控制图 - 位于左下角。当变异主要是由于测量系统错误所致时,X 控制图中的大多数点都在控制限制内。
Excel数据案例:
http://pan.baidu.com/s/1i5AXSRN
6SQ统计3.0企业版90天试用下载 http://pan.baidu.com/s/1i5AXSRN
收起阅读 »
有三个操作员,每人量测5个不同的料件,每个料件测量两次,所以共有30个测量值,。每个料件对操作者都是唯一的,没有任一个料件会同时被两个操作者测量。因此我们选用量具R&R(嵌套的)方法来进行分析
1, 6SQ统计--测量系统分析--量具R&R(嵌套的)

试验次数 2
评价人3
每测试人零件个数 5
点击设计
生成表格,并填入实验数据:
过程公差是10,数据范围选择全部的红色的框内,点击确认 输出分析结果。
解释结果
查看“合计量具 R&R”和“部件之间”的“%贡献”列。部件之间差异的百分比贡献(部件之间 = 17.54)比测量系统变异的百分比贡献(合计量具 R&R = 82.46)小很多。“%研究变异”列表明“合计量具 R&R”占研究变异的 90.81%。因此,大多数变异是由于测量系统错误所致;非常少的一部分变异是由于部件之间的差异所致。请参见测量系统可接受性准则。
可区分类别数为 1 表示测量系统无法区分部件。请参见可区分类别数声明。
查看变异分量图 - 位于左上角。大多数变异是由于测量系统错误(量具 R&R)所致;非常少的一部分变异是由于部件之间的差异所致。
查看 X 控制图 - 位于左下角。当变异主要是由于测量系统错误所致时,X 控制图中的大多数点都在控制限制内。
Excel数据案例:
http://pan.baidu.com/s/1i5AXSRN
6SQ统计3.0企业版90天试用下载 http://pan.baidu.com/s/1i5AXSRN
收起阅读 »