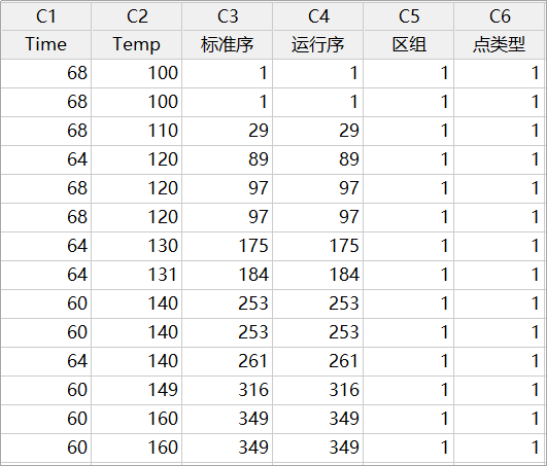
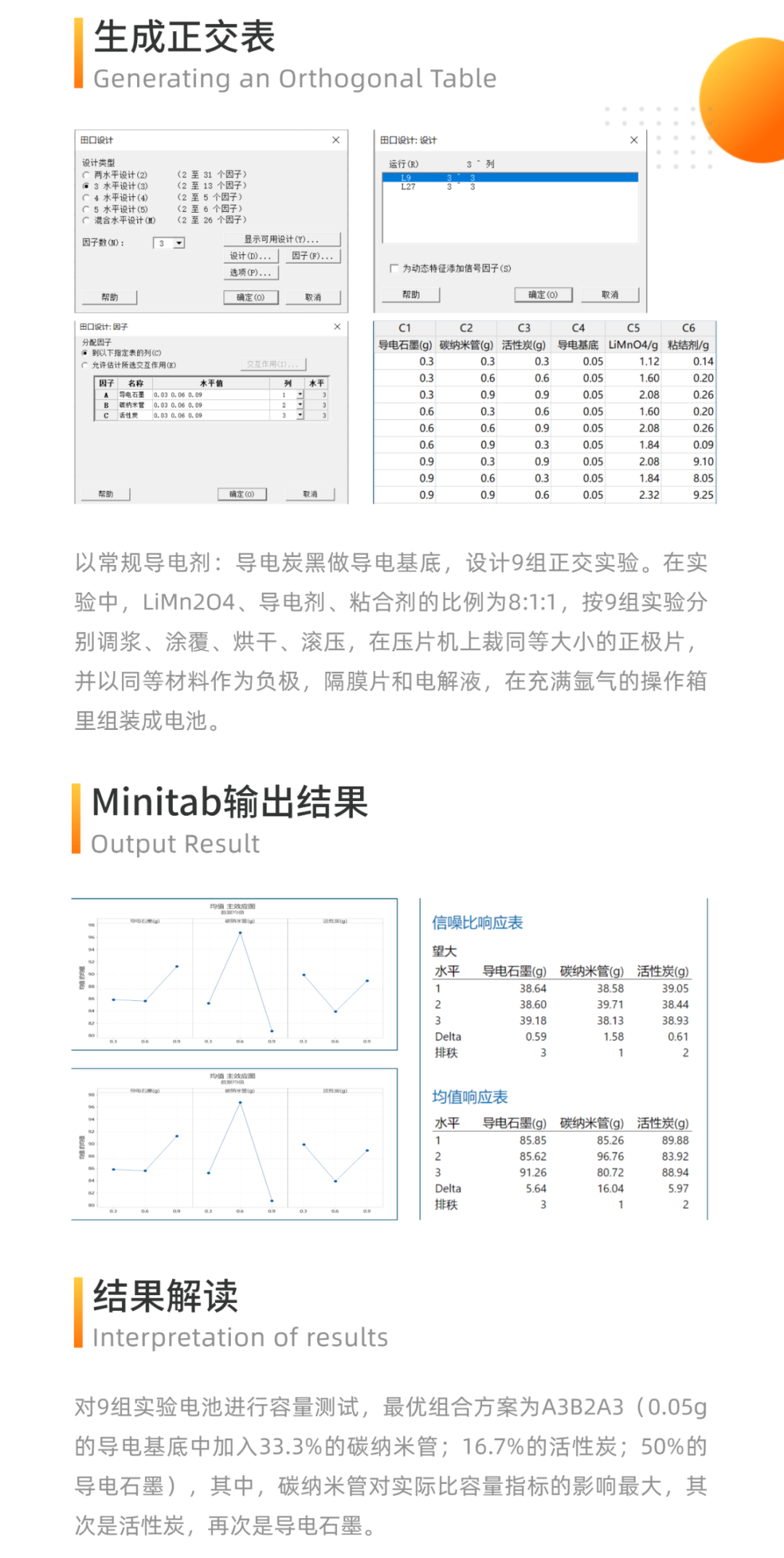
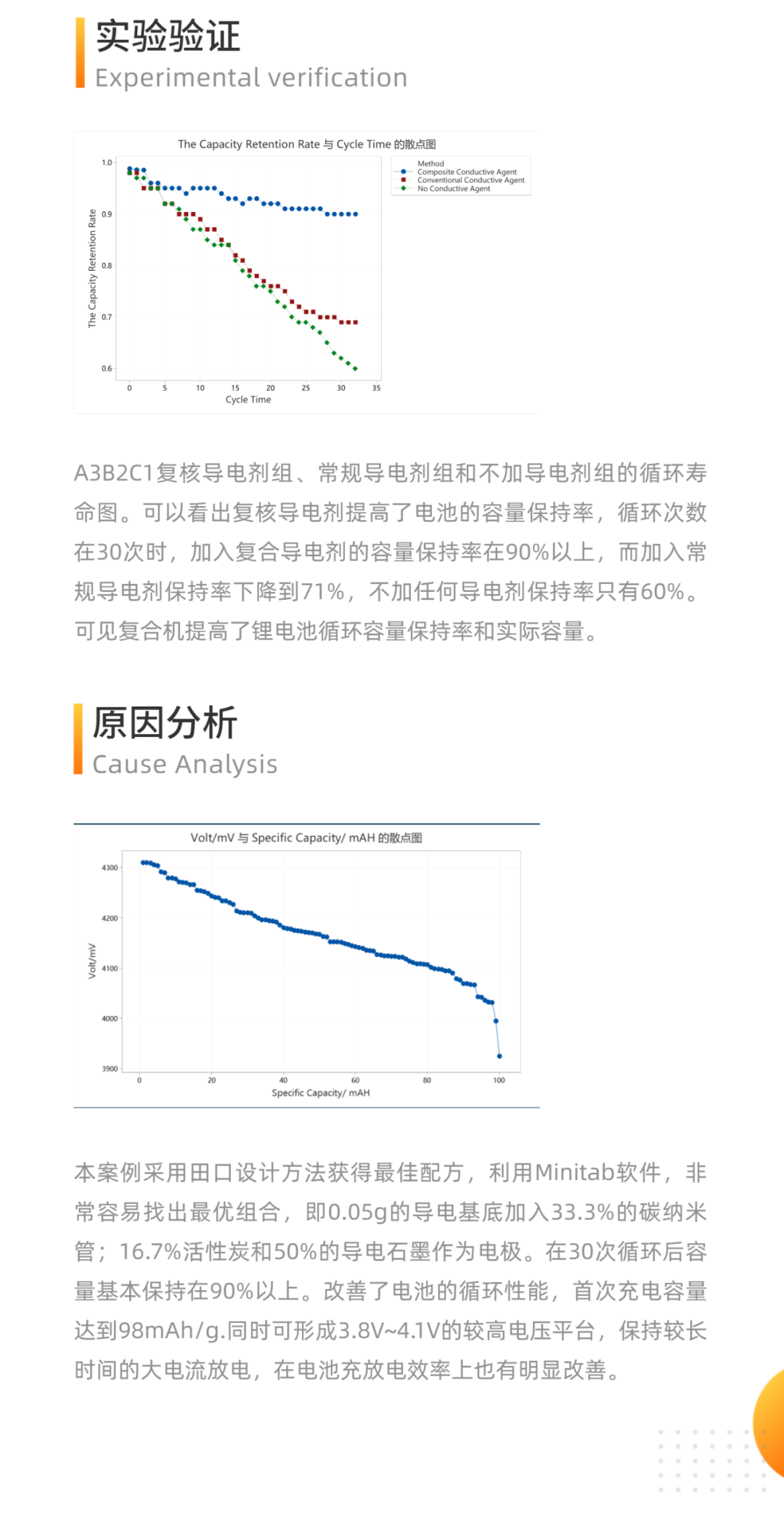
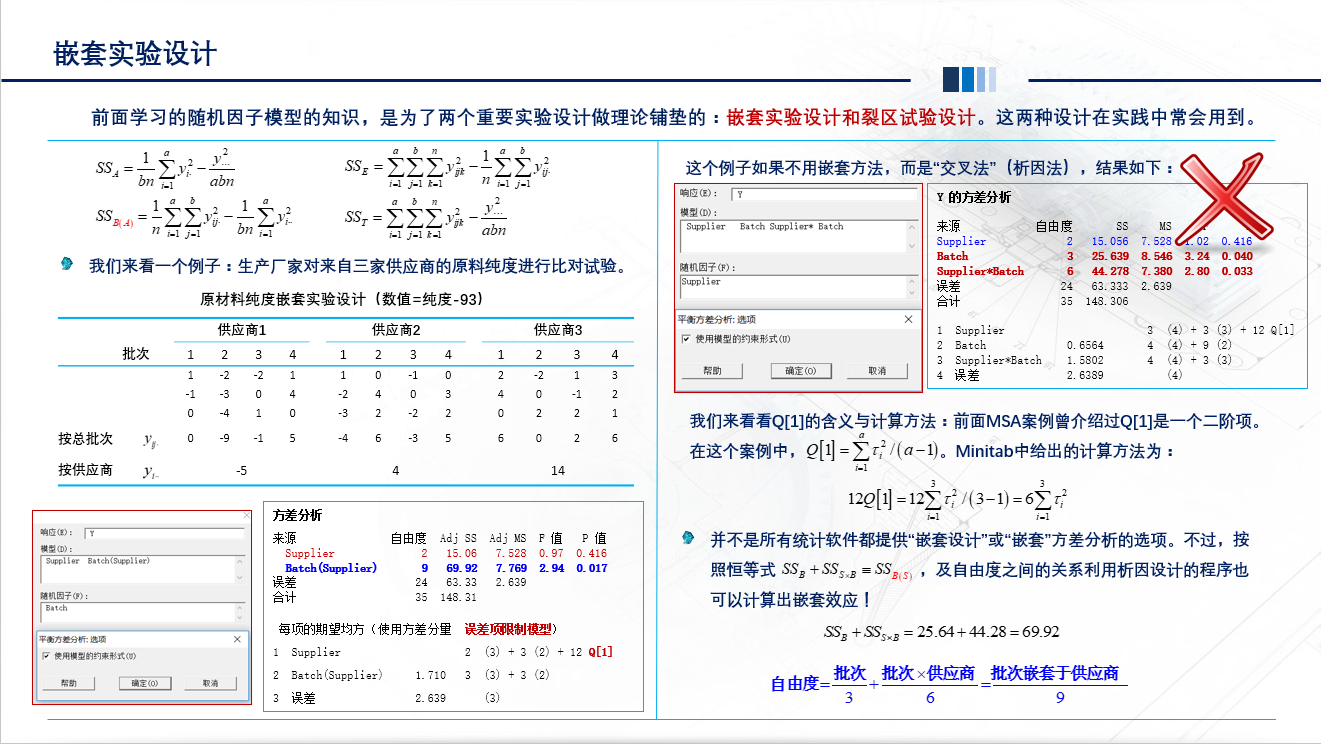
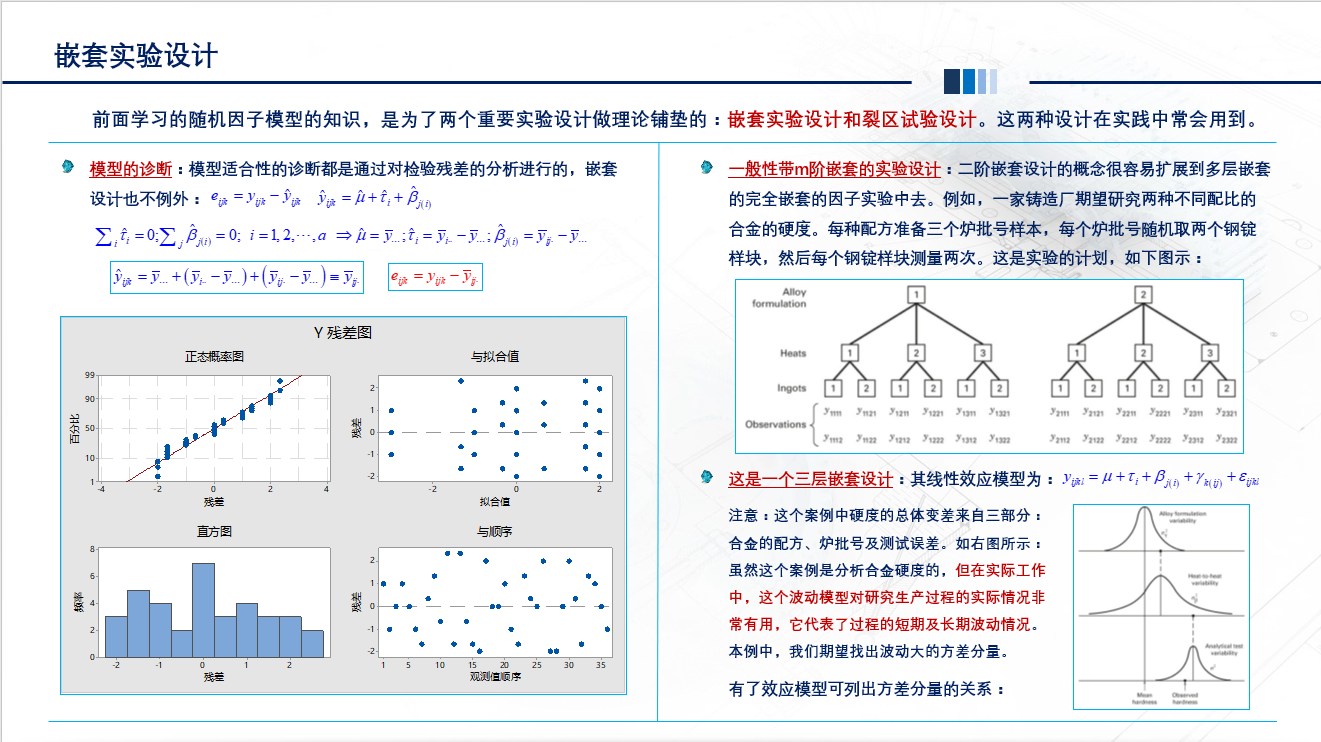
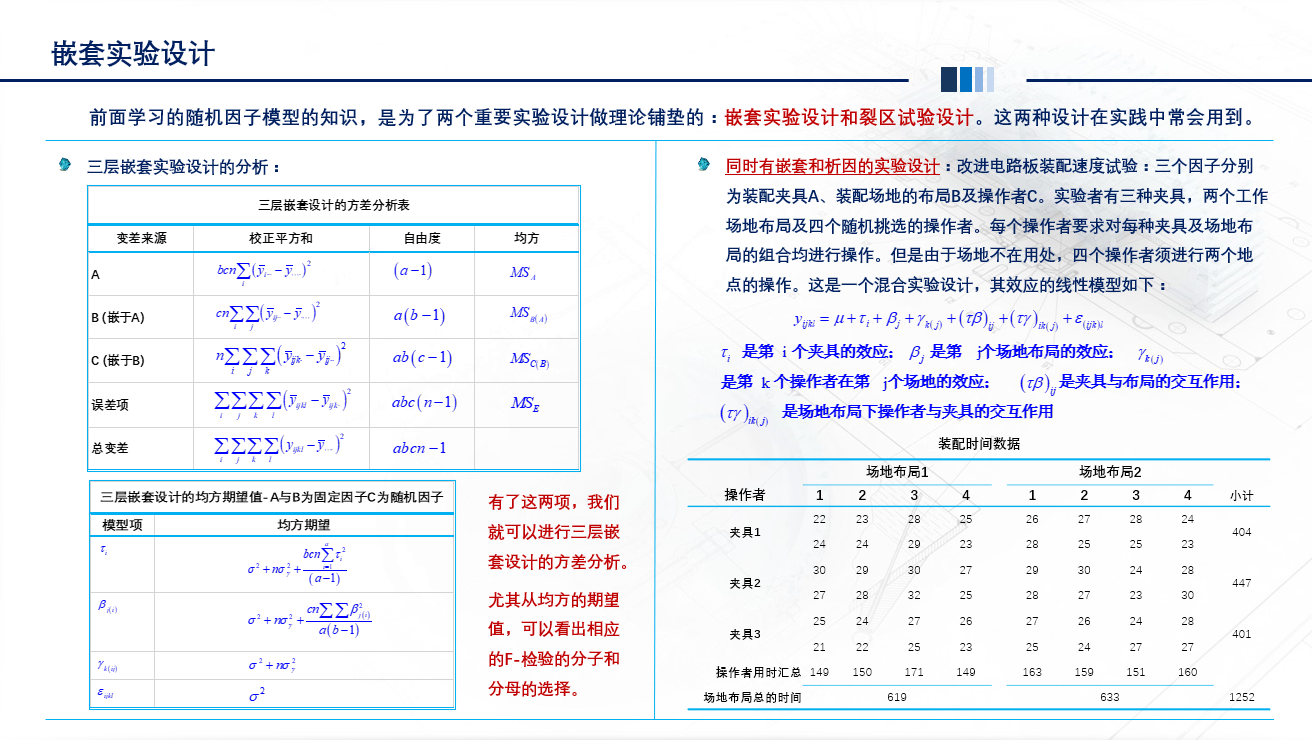
选择实验设计中的最优设计
我们知道,DOE在质量控制的整个过程中扮演了非常重要的角色,它是我们产品质量提高,工艺流程改善的重要保证。但基于实验环境和实验成本等因素考虑,有时,我们并不能够实现所有的因子水平组合。这样我们就需要根据实际场景执行最优设计。
最优设计,是指在给定因子空间内试验单元数相等的所有试验方案中,各回归系数的广义方差最小的试验方案。最优设计是在因子空间中可能产生的试验方案中信息矩阵行列式值最大,也是相关矩阵行列式值最小的试验方案。最优设计的出发点是优化回归方程的统计性质。最优设计试验方案通常用数值方法构造,先给定一个初始方案,然后用计算机构造出一系列方案的信息矩阵行列式值逐渐增大,并收敛于最优设计方案。最优设计有一次模型和二次模型的区别,也有饱和的与非饱和的区别。Minitab 的最优设计功能可以与一般全因子设计、响应曲面设计以及混料设计一起使用。
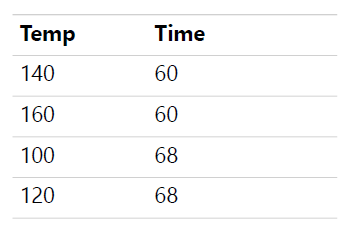
【例】工艺工程师希望建立将导致生物膜厚度及最大拉力的时间和温度设置。 由于这两个因素,她必须小心处理薄膜,因为如果过程运行太冷/太短,薄膜不会固化,如果运行太热/时间太长,薄膜会燃烧。 具体来说,为了让薄膜固化但不燃烧,她有以下限制:
(1)在最短的 60 分钟的循环时间内,它们必须在至少 140 度但不超过 160 度的温度下运行;
(2)在最长的 68 分钟的循环时间内,它们必须在至少 100 度但不超过 120 度的温度下运行。
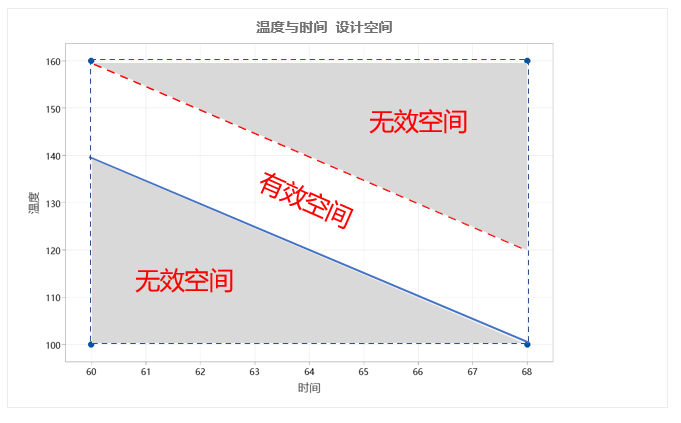
根据这样的要求,就相当于我们执行2因子2水平设计,但是实验区域受限(如下图)
我们可以根据线性回归特性,将边界线的模型表达出来:
Temp=460-5*Time
Temp=440-%*Time
为了得到实验空间,我们借助Minitab软件的产生网格数据,初步得到实验的空间:
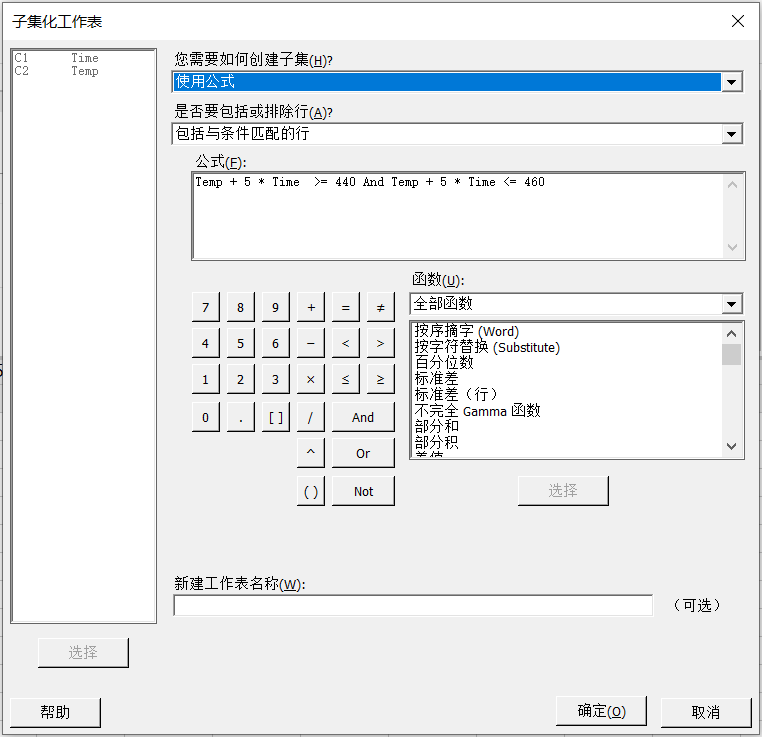
从备选点集中选择设计点以得到最优设计。当原始设计包含的点比限于时间或财力所能实现的多时,通常使用选择最优设计来减少试验数。虽然这些数据点可能是将来的试验点,但根据前面的介绍,有些空间数据并没有实际意义,因此我们需要截取相应的实验点,这个工作可以通过Minitab的子集化工作表实现:
根据子集化工作表的设置,将实验空间进一步优化,如下图所示:
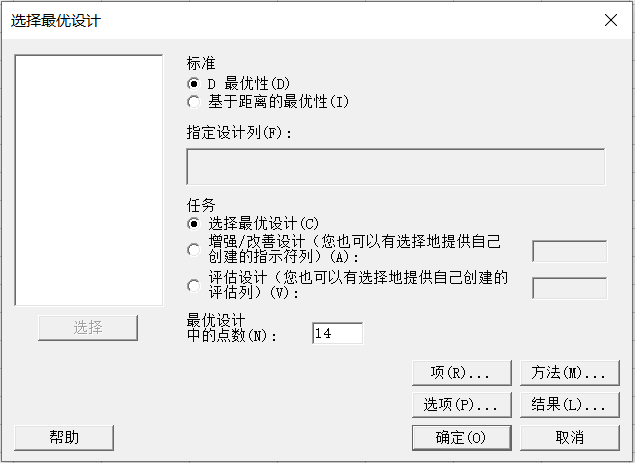
这些实验组内次数非常庞大,基于实验的原则,我们不可能将所有组合全部实施,接下来,利用Minitab的“选择最优设计”可以帮我们快速选择:
这样一来,Minitab就可以从候选设计组合中选择最优的14次运行,基于这些实验结果,Minitab可以拟合出二次回归模型。D 最优性将拟合模型中回归系数的方差降到最低,从而提供最精确的效应估计。
指定模型后,Minitab 将从一组候选设计点中选择满足D 最优标准的设计点。
收起阅读 »
最优设计,是指在给定因子空间内试验单元数相等的所有试验方案中,各回归系数的广义方差最小的试验方案。最优设计是在因子空间中可能产生的试验方案中信息矩阵行列式值最大,也是相关矩阵行列式值最小的试验方案。最优设计的出发点是优化回归方程的统计性质。最优设计试验方案通常用数值方法构造,先给定一个初始方案,然后用计算机构造出一系列方案的信息矩阵行列式值逐渐增大,并收敛于最优设计方案。最优设计有一次模型和二次模型的区别,也有饱和的与非饱和的区别。Minitab 的最优设计功能可以与一般全因子设计、响应曲面设计以及混料设计一起使用。
【例】工艺工程师希望建立将导致生物膜厚度及最大拉力的时间和温度设置。 由于这两个因素,她必须小心处理薄膜,因为如果过程运行太冷/太短,薄膜不会固化,如果运行太热/时间太长,薄膜会燃烧。 具体来说,为了让薄膜固化但不燃烧,她有以下限制:
(1)在最短的 60 分钟的循环时间内,它们必须在至少 140 度但不超过 160 度的温度下运行;
(2)在最长的 68 分钟的循环时间内,它们必须在至少 100 度但不超过 120 度的温度下运行。
根据这样的要求,就相当于我们执行2因子2水平设计,但是实验区域受限(如下图)
我们可以根据线性回归特性,将边界线的模型表达出来:
Temp=460-5*Time
Temp=440-%*Time
为了得到实验空间,我们借助Minitab软件的产生网格数据,初步得到实验的空间:
从备选点集中选择设计点以得到最优设计。当原始设计包含的点比限于时间或财力所能实现的多时,通常使用选择最优设计来减少试验数。虽然这些数据点可能是将来的试验点,但根据前面的介绍,有些空间数据并没有实际意义,因此我们需要截取相应的实验点,这个工作可以通过Minitab的子集化工作表实现:
根据子集化工作表的设置,将实验空间进一步优化,如下图所示:
这些实验组内次数非常庞大,基于实验的原则,我们不可能将所有组合全部实施,接下来,利用Minitab的“选择最优设计”可以帮我们快速选择:
这样一来,Minitab就可以从候选设计组合中选择最优的14次运行,基于这些实验结果,Minitab可以拟合出二次回归模型。D 最优性将拟合模型中回归系数的方差降到最低,从而提供最精确的效应估计。
指定模型后,Minitab 将从一组候选设计点中选择满足D 最优标准的设计点。
收起阅读 »
预测分析:帮助规划 DOE 的完美合作伙伴
实验设计有显着的好处。它们可用于多种情况,并有效地允许操纵多个输入因素以确定它们对所需响应的影响。他们还确定了在一次试验一个因素时可能会遗漏的重要交互作用。
DOE 的规划阶段对于成功至关重要。由于在规划阶段发现的障碍,DOE 经常停滞不前。例如,看起来过于昂贵或复杂或缺乏关键信息的 DOE 通常在它们有机会执行之前就被废弃了。幸运的是,先进的预测分析 是一个强大的工具,可以帮助消除创建 DOE 的障碍,甚至可以提高成功的机会。
问题 1:您想运行筛选设计,但您不能停止系统(或进程)运行以收集数据或收集数据非常昂贵。
从业者使用筛选实验设计(筛选 DOE)从许多潜在变量的领域中识别过程中最重要的变量。它们使从业者能够减少实验的规模,从而节省时间和金钱。如果数据难以获取或成本高昂,则尤其如此。
当您无法停止系统或进程来运行筛选实验时会发生什么?或者,如果收集用于筛选的数据点非常昂贵,以至于难以证明这样做是合理的?
解决方案 1:预测分析可以帮助您轻松识别最重要的变量。
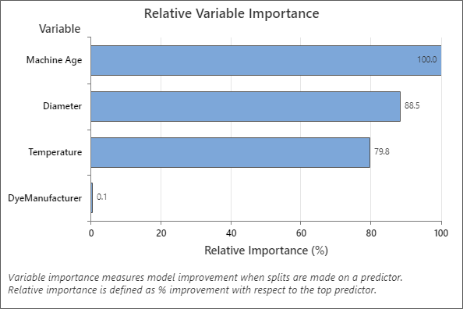
不要害怕,预测分析就在这里!通过分析来自您的系统或流程的数据,您可以利用您最喜欢的机器学习算法或运行自动化机器学习来识别对您的响应有潜在影响的预测因素。Minitab 通过我们专为帮助您识别最重要的变量而构建的相对变量重要性图表使这一过程变得简单。查看我们的网络研讨会 DOE 实践,链接如下示例。
问题 2:您想运行设计实验,但对因素(即水平)的适当范围(即上限和下限)不确定。
运行 DOE 时,实验在不同的因子值(称为水平)下运行。这些水平是我们衡量响应的自变量,我们传统上将其称为因变量。例如,如果您尝试优化一台设备的速度,则需要设置最高和最低速度的限制以构建速度范围以优化您的过程。另一个例子可能是烘烤蛋糕时烤箱的温度。根据您的经验,您可能知道低于 300F 不会烘烤蛋糕,而在 400F 时会烧焦,因此您可以设置限制。但是,如果您以前从未烤过蛋糕怎么办?或者,如果您有一台新机器而不知道在哪里设置限制怎么办?
解决方案 2:预测分析提供可视化效果来帮助您设置合理的限制。
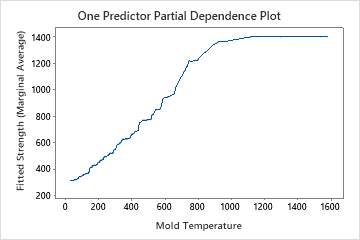
当您运行 Minitab 的预测分析时,您将生成可视化效果,展示一个或多个变量对预测结果的影响。为了预测结果,这些图的目的是突出响应和变量之间的关系是线性的、单调的还是更复杂的。这些可视化对于 DOE 也非常有用。
在上面的示例中,假设您正在尝试运行优化强度的实验。您可能了解模具温度与强度之间的关系,但也知道简单地将机器调到最高温度可能会产生不利影响,例如过热或不必要地增加生产成本。您还知道实验中可能会与其他变量(例如压力)发生相互作用。通过查看图表,您会发现温度高于 1200 会导致强度边际增加。对于您设计的实验,您可以将模具温度水平设置为 1000 和 1200,以运行以最大化强度为目标的实验。但是,如果目标是最小化强度,您可以从图中看出,在较低的模具温度范围内进行测试会更合理。
预测分析只是与 DOE 携手并进的众多工具之一。
DOE 是许多从业者的重要工具,不应孤立存在。如前所述,规划对于 DOE 的成功至关重要,这就是 Minitab 创建专门为帮助规划过程而构建的DOE 规划工作表的原因。如果您是 DOE 的新手或只是想提高您的技能组合,Minitab 会提供支持、资源和解决方案来帮助您前进。 收起阅读 »
DOE 的规划阶段对于成功至关重要。由于在规划阶段发现的障碍,DOE 经常停滞不前。例如,看起来过于昂贵或复杂或缺乏关键信息的 DOE 通常在它们有机会执行之前就被废弃了。幸运的是,先进的预测分析 是一个强大的工具,可以帮助消除创建 DOE 的障碍,甚至可以提高成功的机会。
问题 1:您想运行筛选设计,但您不能停止系统(或进程)运行以收集数据或收集数据非常昂贵。
从业者使用筛选实验设计(筛选 DOE)从许多潜在变量的领域中识别过程中最重要的变量。它们使从业者能够减少实验的规模,从而节省时间和金钱。如果数据难以获取或成本高昂,则尤其如此。
当您无法停止系统或进程来运行筛选实验时会发生什么?或者,如果收集用于筛选的数据点非常昂贵,以至于难以证明这样做是合理的?
解决方案 1:预测分析可以帮助您轻松识别最重要的变量。
不要害怕,预测分析就在这里!通过分析来自您的系统或流程的数据,您可以利用您最喜欢的机器学习算法或运行自动化机器学习来识别对您的响应有潜在影响的预测因素。Minitab 通过我们专为帮助您识别最重要的变量而构建的相对变量重要性图表使这一过程变得简单。查看我们的网络研讨会 DOE 实践,链接如下示例。
问题 2:您想运行设计实验,但对因素(即水平)的适当范围(即上限和下限)不确定。
运行 DOE 时,实验在不同的因子值(称为水平)下运行。这些水平是我们衡量响应的自变量,我们传统上将其称为因变量。例如,如果您尝试优化一台设备的速度,则需要设置最高和最低速度的限制以构建速度范围以优化您的过程。另一个例子可能是烘烤蛋糕时烤箱的温度。根据您的经验,您可能知道低于 300F 不会烘烤蛋糕,而在 400F 时会烧焦,因此您可以设置限制。但是,如果您以前从未烤过蛋糕怎么办?或者,如果您有一台新机器而不知道在哪里设置限制怎么办?
解决方案 2:预测分析提供可视化效果来帮助您设置合理的限制。
当您运行 Minitab 的预测分析时,您将生成可视化效果,展示一个或多个变量对预测结果的影响。为了预测结果,这些图的目的是突出响应和变量之间的关系是线性的、单调的还是更复杂的。这些可视化对于 DOE 也非常有用。
在上面的示例中,假设您正在尝试运行优化强度的实验。您可能了解模具温度与强度之间的关系,但也知道简单地将机器调到最高温度可能会产生不利影响,例如过热或不必要地增加生产成本。您还知道实验中可能会与其他变量(例如压力)发生相互作用。通过查看图表,您会发现温度高于 1200 会导致强度边际增加。对于您设计的实验,您可以将模具温度水平设置为 1000 和 1200,以运行以最大化强度为目标的实验。但是,如果目标是最小化强度,您可以从图中看出,在较低的模具温度范围内进行测试会更合理。
预测分析只是与 DOE 携手并进的众多工具之一。
DOE 是许多从业者的重要工具,不应孤立存在。如前所述,规划对于 DOE 的成功至关重要,这就是 Minitab 创建专门为帮助规划过程而构建的DOE 规划工作表的原因。如果您是 DOE 的新手或只是想提高您的技能组合,Minitab 会提供支持、资源和解决方案来帮助您前进。 收起阅读 »
半导体制造商提高质量和产量的 4 个步骤
半导体制造不仅是技术最先进的行业之一,而且也是成本最密集的行业之一。随着基于半导体的设备在从个人电脑到电话和汽车的一切事物中变得司空见惯,需求持续增长。随着数量的增加,对更强大的质量计划的需求也在增加。虽然大多数制造商都在使用 Minitab 等统计软件来解决某些问题,但仍有机会扩大其范围并提供更多价值。
半导体制造业往往比其他行业平均收集更多的数据。这意味着您可以更轻松地将数据以不同的方式发挥作用,例如:
使用测量系统分析最大限度地减少生产中的变化
使用量具 R&R 和方差分析等工具来确定测量系统的变化至关重要,尤其是对于半导体制造而言。为确保规格能够得到保证,测量的可重复性和再现性需要相对于测量的规格公差较小。 Minitab 的新测量系统分析 模块使各级从业人员能够轻松评估测量系统的变异、偏差和稳定性。
使用统计过程控制来提高产量并避免制造过程中的浪费
使用控制图和能力分析来测量关键特性,如晶圆厚度、沉积速率(晶圆表面沉积材料作为薄层以包含电气特性的速率)、终点时间(检测最准确的停止时间蚀刻工艺,以避免蚀刻过度或蚀刻不足)等将有助于确保您的工艺和设备处于可控状态。如果您已经在使用 SPC 方法,使用Minitab的 下一代统计过程控制可以帮助您改进技术并实现实时节省。
使用实验设计改进制造工艺
由于半导体制造由多个复杂的过程组成,即使是最有经验和能力的工程师也不一定知道制造设备的最佳设置。即使已知最佳设置,新技术也会不断被采用,从而引入未知情况和新问题。实验设计帮助工程师建立一个综合模型,以帮助非常准确地理解系统的工作原理。 通过阅读这篇博文,了解更多关于 DOE 的实际操作,帮助提高一个制造商抛光过程的均匀度,或者通过观看本次网络研讨会,了解更多关于 DOE 的总体信息。
使用机器学习进行硅后验证
与进行测量并做出通过/失败决策的生产测试不同,在硅后验证中,您需要非常详细地了解设备在各种操作条件下的行为。使用机器学习,您可以更好地了解设备的输入如何影响输出并找到它们之间隐藏的关系和复杂性。借助Minitab 的预测分析模块,您可以构建稳健的预测模型或使用我们的可变重要性图表等工具来突出显示影响性能的最关键输入。
收起阅读 »
半导体制造业往往比其他行业平均收集更多的数据。这意味着您可以更轻松地将数据以不同的方式发挥作用,例如:
使用测量系统分析最大限度地减少生产中的变化
使用量具 R&R 和方差分析等工具来确定测量系统的变化至关重要,尤其是对于半导体制造而言。为确保规格能够得到保证,测量的可重复性和再现性需要相对于测量的规格公差较小。 Minitab 的新测量系统分析 模块使各级从业人员能够轻松评估测量系统的变异、偏差和稳定性。
使用统计过程控制来提高产量并避免制造过程中的浪费
使用控制图和能力分析来测量关键特性,如晶圆厚度、沉积速率(晶圆表面沉积材料作为薄层以包含电气特性的速率)、终点时间(检测最准确的停止时间蚀刻工艺,以避免蚀刻过度或蚀刻不足)等将有助于确保您的工艺和设备处于可控状态。如果您已经在使用 SPC 方法,使用Minitab的 下一代统计过程控制可以帮助您改进技术并实现实时节省。
使用实验设计改进制造工艺
由于半导体制造由多个复杂的过程组成,即使是最有经验和能力的工程师也不一定知道制造设备的最佳设置。即使已知最佳设置,新技术也会不断被采用,从而引入未知情况和新问题。实验设计帮助工程师建立一个综合模型,以帮助非常准确地理解系统的工作原理。 通过阅读这篇博文,了解更多关于 DOE 的实际操作,帮助提高一个制造商抛光过程的均匀度,或者通过观看本次网络研讨会,了解更多关于 DOE 的总体信息。
使用机器学习进行硅后验证
与进行测量并做出通过/失败决策的生产测试不同,在硅后验证中,您需要非常详细地了解设备在各种操作条件下的行为。使用机器学习,您可以更好地了解设备的输入如何影响输出并找到它们之间隐藏的关系和复杂性。借助Minitab 的预测分析模块,您可以构建稳健的预测模型或使用我们的可变重要性图表等工具来突出显示影响性能的最关键输入。
收起阅读 »
稳健性设计的逻辑
稳健性设计是正交设计之后的里程碑式的创新,但不能等同于田口方法。
上世纪初农业已有稳健性设计的实践,希望大麦新品种在肥力不同的土地、气候条件不同的地区,仍能有稳产的稳健性。
中国和欧美学者对稳健性设计逻辑的理解与田口方法对稳健性设计逻辑的理解,有共识也有分歧。
国内典型的文献是《正交法与应用数学》(作者张里千),美方文献《试验设计与分布及参数优化》(作者吴建福)。田口方法典型文献是《稳健参数设计》(作者韩之俊)
过去,当产品质量可靠性、稳定性差时,设计产品的工程师认为产品经实验室检验没问题,所以会归罪于批量生产线的质控不严和用户使用不当。
比如在批量生产时,成品各零部件质量特性的变异(噪声)必然使批量成品质量波动变大,
如用公差小的零部件成本高,性价比差。
而零部件组合产生的负面交互效应(噪声),如不做正交试验,可能不知道这种负面交互作用的存在,也不知道正面交互作用的增益。
农村电压忽高忽低的波动(外噪声)会降低电器功能,这种噪声用户无法控制。
而田口先生发现,如在试验中加入模拟噪声的因子,可利用质量特性与参数组合之间的非线性效应,能降低内部干扰因子的影响,利用可控因子抑制噪声因子的交互作用,能减少噪声因子对响应的干扰。只需调整水平组合(即参数设计),基本不增加费用,就能抑制内外噪声对响应的干扰。或者说,对噪声不敏感。而且能确定最合理的公差范围(容差设计,也可理解为价值工程),即是稳健性设计。
田口方法的试验设计和其它DOE方法不同,甚至于相悖。
传统实验室试验时需要排除噪声干扰。而稳健性设计相反,试验时加入模拟干扰响应的内外噪声因子,达到实验室设计的产品质量特性值和受内外噪声干扰下实际使用环境有一致性。
田口方法正交设计用分内表和外表的直积表,把可控因子正交表称内表,噪声因子正交表称外表。
要求可控因子内表的每一个组合,都要和噪声因子外表的每一个组合一起进行试验。用信噪比度量稳健性,评估出均值趋近目标值,方差又小的最佳的组合。
有学者认为直积表本质是“裂区法”或“分割试验法”,但稳健性设计的内在逻辑,常被误解。
部分析因设计的问题。
多因子案例用部分析因设计是经济的方法。
谢宁方法否定部分析因设计,只认可全因子析因设计。但在可控因子远多于4因子案例时,仅挑选出少量显著性因子组成的全因子析因设计可能遗漏掉不少有价值的信息。比如某案例“A和B都是不显著性因子,但AxB交互作用是显著性因子。”(韩文p55)
谢宁方法忽略了不显著性因子潜在的正面效应,而且统计意义上不显著不等于实际意义上无用。
传统DOE常用二分之一或四分之一的全因子析因设计,然后对活跃因子补充试验,凑成活跃因子群的全因子析因设计数据集合。全因子析因设计对建数模是必需的,其缺点是假设最优水平组合在上述活跃因子群框架内。建立的数模是精简的,但试验水平范围不足够,样本量太小,其数模可能仅仅拟合样本,并非反映总体全貌。
田口方法内表常用部分析因设计,但静态稳健性设计以寻找最优水平组合为目的,所以交互作用混淆不是大问题,其软肋是常用L18大正交表为内表的直积法功效低,内表用部分析因设计会漏掉更优可控因子组合。
怎样解决部分析因设计信息不完备弱点呢?国内学者建议尽可能用小正交表和饱和正交表。首次试验后,在好的水平基础上再調整出新的水平,进入下一轮新的水平组合试验。
如同“盲人爬山”,探一步,爬一步,经多轮正交试验,但仍能在混杂的信息中找到最优组合的方向。这是“笨”办公,但新的水平组合,会带来新的信息,能逐步逼近最优水平组合。
新的试验水平框架可能带来质变:当水平变动后,可能原不活跃因子和不显著性交互作用会“变性”。
(三)方差分析工具。
传统正交试验,为了筛去不显著性因子,在部分析因设计前提下用方差分析工具。
张里千认为:“部分实施会造成混杂,不足以施行方差分析。”(张文p19)
BOX认为“很多电脑程序都利用方差分析表来分析2k设计和它的部分设计,但是分析这种特殊的设计时,使用ANOVA会非常令人费解,并且没有什么意义。”(《试验应用统计》p115)
而且理论上实施方差分析,残差需以下假设为前提:正态分布、均值为零、数据相互独立、方差相等。(韩文p23)而在实际应用时,很少会验证上述假设。
在实际案例中“噪声分布并不一定要服从正态分布”、“相同的变异性假设在稳健参数设计中不存在。”(韩文p4)
国内的实践证明:“经过逐批少数正交试验便能绕过处理试验误差的统计方法过程,进入到良好的位级组合区域。”(张文p4)
简言之:既然部分析因设计无法精确量化主效应和交互效应,不用方差分析等精确工具,而用极差法、因子趋势图等近似工具分析,用多轮正交试验逐步找到最佳水平组合。
(四)对直积表的争议。
田口方法的直积表被批判试验次数多,以及内表常用部分析因设计和非正规正交表,造成交互效应混杂被诟病。
直积表的复杂目的是,用试验寻找随机变量噪声因子集合对响应的干扰最小的可控因子组合。这是稳健性设计的核心精髓,可是很少人能理解其科学意义。
实际上在多因子案例,传统方法有的还用6次重复试验,总次数也不少。
对直积表试验次数太多的缺点,有学者提出用一个“复合噪声因子”取代多噪声外表(韩文p72),这样经济上合算,实际不合理。
“如果研究人员知道噪声因子和控制因子是怎样联合地影响变差的,就没必要实施参数设计试验。”(吴文p410)
又有学者提出用“组合表”替代直积表,即噪声因子和可控因子同在一个全因子析因设计的正交表内。
这“近似”符合直积表,说近似符合,这方法把噪声因子视为常量,而实际是随机变量。多噪声外表常用全因子析因设计,为了能显示“噪声X噪声”交互作用,多噪声之间交互作用比单噪声因子对响应的影响更复杂。而“组合表”只能显示单噪声因子和可控因子之间交互作用。
比如电压和频率波动的噪声因子交互作用比单电压波动对电器功能干扰更大,尤其噪声X噪声对响应的干扰,往往只能在试验中显示。
如多因子多噪声因子案例,因子总数过大,“组合表”只能用部分析因设计时,无法得到全因子析因设计的全面数据,这也是直积法内表常用部分析因设计的缺陷之一。
所以直积法能最精确显示噪声因子群对响应的影响,但有可简化和完善的余地。
如可计算案例,直积法的复杂不成问题。
比如电工类有公式,可用计算方法替代试验。多水平、多因子案例,如用全因子析因设计的直积表,因子和水平数再多也不成问题。
国内学者用对参数约束性计算,又能大大减少计算量,有的案例,一轮约束性试验达到三轮非约束性试验的效果。最后用重复试验验证。
(五)对关注点差异。
传统DOE目的是回归建模,在实验设计时尽可能分清因子主效应和交互效应,减少混杂。
而田口方法用逆传统设计:
“任一个含Q(噪声因子)的二因子交互作用是强纯净的”(吴文p132),
传统正交试验, “通常优先考虑的是主效应的估计,而不是两因子交互效应。”(吴文p238)
“将分辨度以及最小低阶混杂准则,应用于参数设计试验是不合适的。”(吴文p407)
吴建福对稳健性设计逻辑的理解:
稳健性设计认为能抑制噪声的“可控X噪声”的交互效应,和主效应同等重要,而且比“可控X可控”交互效应更重要。
能抑制噪声的“可控X可控X噪声 ”的高阶交互效应和“可控X可控”交互效 应同等重要,这颠覆了高阶交互效应可忽略的惯例。(吴文有实例p407)
(六)可控因子之间交互作用定性问题。
传统DOE认为田口方法最大问题是交互作用混杂,其实最大理论问题是对可控因子之间交互作用的解释。
正交设计解决了显示交互作用问题,想不到田口方法认为可控因子之间的交互作用对稳健性设计是“有害的”。而且又武断认为可控因子和噪声因子交互作用“有利的”。(韩文p4)
在没用稳健性设计之前可控因子和噪声因子交互作用也客观存在的,多数对响应有害的,因此才需要调节可控因子水平组合,抑制噪声因子对响应的干扰,所以不能说可控因子和噪声因子之间交互作用都是有利的。
而稳健性设计找出能抑制噪声因子的非线性响应可控因子,和找到各可控因子水平巧妙组合(其中有可控因子之间交互作用)抑制了噪声因子,这时可控因子和噪声因子交互作用才是有利的。
“A有两个水平A1、A2,当另外一个因子B处于B1水平吋,A1水平的结果和A2水平的结果相比有一个量值;当B处于B2水平时,A1水平的结果和A2水平的结果相比量值有了变化。因此,交互作用就是因子影响结果的不一致或不再现。”(韩文p3)
“交互作用会导致结论不一致或不再现,所以必须尽量避免可控因子之间的交互作用…”(韩文p9)
上述交互作用“有害的”原理实际上生产过程中对可控因子水平控制的难度问题。
对于难以控制的水平,稳健性设计可把可控因子视为噪声因子处理,比如难控制的温度问题。
众所周知,正交设计能显示正面交互作用和负面交互作用:
利用正面交互作用获得1+1大于2的额外增益,对负面交互作用,可改变设计组合减弱之。
吴文中案例,“可控X可控X噪声”交互作用,是可控因子之间交互作用起到抑制噪声作用。
韩文p29中案例:钢硬度由时间和温度交互作用占33%,请问能消除交互作用吗?
青铜的硬度是銅和锡的交互效应占主导,怎样解释?
(七)处理交互作用混杂问题。
“交互作用是客观存在的,怎样避免或消除呢?回答是交互作用的存在取决于应用什么样的测量系统进行分析。”、“用信噪比,特别是动态特性的信噪比…”(韩文p5)
田口方法认为用特殊正交表、输出特性连续性计量、信噪比度量,“一般情况下,可控因子之间的交互作用会消除殊尽。”(韩文p17)
“用特殊正交表L12(211), L18(2x37)任意两列的交互作用平均分配在各个列上。”(韩文P6)
L12是飽和设计,交互作用“平均分配在各列上”的说法是自圆其说。实际上各列交互作用混杂、重叠,平均分配说法是难令人信服。
多因子案例用部分析因设计是经济的方法,虽然主效应和交互作用混杂,但其综合的效应,正面或负面效应以及高阶交互效应都反映在响应上,而且是真实数据,仅有试验误差。
笔者猜测,田口方法对可控因子之间交互作用有害的种种解释,为了回应内表用部分析因设计造成交互作用混杂的质疑,但反而令人困惑不解。
历史上工业应用正交设计远晚于农业,由于工业参数远多于农业,用全因子析因设计经济上有困难,而田口先生勇于在工业上用部分析因设计是大功臣。
国内实践证明,如不建数模,交互效应混杂不影响用多轮正交试验逐步找到最优水平组合。
“数学要经得起思维逻辑严密性推敲或者在其他科学领域应用的有效性来检验,而统计学则更多地要得到实际的直接检验。”(《试验应用统计》译者序)
(八)试验设计方法的科学性是源头。
“分贝值表示的SN比,不仅计算方便,而且可使经对数变换的η(信噪比)更接近于正态分布…同时因素效应大多具有可加性,忽略了交互作用的影响。”(《稳健性设计》曾凤章p63)
上述文献讲清楚了田口方法认为用对数变换后的信噪比能“忽略”交互作用的原理。
实际上传统建模方法常用数据变换,把非线性性转换成简单的线性模式。
对均值平方和方差对数转换后成线性化的信噪比,这仅是数学形式变化,客观存在 的交互作用还是存在的。如有负面交互作用,也只能調节水平组合来改善,无法用试验后的数据变换来忽略交互作用的本质。
例如学校为改变学习成绩分数至上状态,改用优、良、中、差评估,仍无法摆脱分数评价体制。
田口方法认为稳健性设计就是用信噪比的正交实验设计。对此议提出异议之前,先澄清一个大前提,噪声因子加入正交试验是稳健性设计关键性的源头,但不是信噪比的功劳。
“试验设计能够用来产生良性数据,甚至可以认为,好的试验设计对科学进步是必不可少的。然而,至今我们更多地注意着数据分析。试验设计具有第一重要性,其原因是,数据的信息内容在进行试验时才确定,任何敏感的分析都不能揭示没有体现在数据中的信息。”(《非线性回归分析及其应用》p134)
比如谢宁方法常用“逐个替换”单因子试验,很难显示交互作用。多因子同时变动的正交设计能显示交互作用。
稳健性设计核心是模拟内外噪声因子参于正交试验,以及怎样调整优化水平组合。用信噪比选优,仅属数据分析的一种方法,而且又有缺陷。
在用信噪比选优方法中,对望大、小型案例选优无难度,争议也少,难度在望目型。
田口方法推荐的2步法:先找出信噪比最大的离散因子。但信噪比大,可能均值相对于方差大,但单均值大对望目型无意义。
望目型信噪比:期望平方/方差。
比如均值(期望)平方10,方差1,但目标值是8。所以必须找到把均值趋向目标值,又不影响方差的独立的位置因子。无这位置因子配套,信噪比大无意义,即望目型信噪比缺少一个目标值参数介入。
而且2步法不是都能实现,运气好的正相关案例:调节后响应方差趋小时,均值趋向目标值。反之,有的案例无位置因子时,方差趋小时,均值远离目标值。这时需方差和“离目差”(均值与目标值差)之间的社会质量经济损失大小,找到一个平衡点,田口创立的质量经济损失公式,能解决这难题:如响应是正态分布,分布对目标值的偏差均方=响应分布方差+均值与目标值差的平方。
田口认为质量特性值偏离目标值就发生质量经济损失,以这定义创立的质量经济损失公式(偏差均方),虽不完美,但因包含响应分布的均值、方差和目标值3个参数,就是优于望目型信噪比的原因。
国内学者把田口方法内表称为选优表,方法是对望目型案例内表组合数据直接用偏差均方选优。
某文献25组试验中只有5组偏差均方靠谱,仅甪这5組和噪声组合一一试验,大大减少了试验次数。而如用田口的直积表,有20组在无噪声因子介入响应时,响应已超合格限,再介入噪声因子做试验是做无用功。
北大学者在实践中证明:“凡偏差均方好(小)时,信噪比也必然好(大),反之不一定成立。”(《正交法和三次设计》P129)在望大望小型案例,偏差均方也适用。
国内有学者认为信噪比适用于动态稳健性设计,用β灵敏度取代均值。静态稳健性设计望目型适用偏差均方。
收起阅读 »
5个分析工具来改善你的机械工程简历、职业和知识
挑战的一部分(和乐趣!作为一名机械工程师,不断寻求改进的机会。无论是你的产品还是过程,机械工程师都有责任找出问题并进行实验来改进它们。是时候花点时间让自己成为更好的工程师了吗?学习和利用这些分析工具不仅能帮助你做得更好,还能为你提供更多的工具来应对新的和令人兴奋的挑战。
1. 使用可视化识别产品中的问题。在可能的情况下,收集常用的数据并绘制成图表直方图、帕累托图、热图甚至相关图. Minitab的新图形生成器使您能够轻松地可视化您的数据,并看到您从未考虑过的可视化效果。
2. 使用过程分析工具识别问题。无论您是否已经识别出问题,过程分析工具都可以帮助您回顾过程,以识别失败的地方或改进的机会。故障模式和影响分析,也称为FMEAs,帮助您评估风险和流程图或流程图可以帮助你快速锁定需要关注的区域。
3. 使用控制图评估过程稳定性。机械工程师应该监控他们的过程,以确保质量和一致性。有许多统计工具,如控制图和能力分析这有助于机械工程师监控过程中的变化,并确定过程是否会生产出符合要求规格的产品。Minitab支持的实时SPC提供即时警报和分析,以确保流程稳定、高效和有能力。
4. 使用产品开发工具和方法设计和开发原型。在使用CAD系统之前,你应该使用许多产品开发工具。将产品推向市场需要对客户的需求和需求有充分的了解,以及严格的方法。学习如何使用决策矩阵工具就像质量矩阵或Pugh矩阵或向这家医疗设备制造商学习,他们利用客户总结和Kano模型的声音,以迅雷不及掩耳之势将新产品推向市场。如果您有兴趣了解产品开发方法(以及更多!),请查看我们的结构化问题解决方法周期表.
5. 利用实验设计。实验设计(DOE)是一种系统的、严谨的解决问题的方法,它确保产生有效的、可辩护的和可支持的结论。它可以有效地解决一般问题,以及改善或优化产品设计和制造过程。机械工程师可以使用DOE来:确定适当的设计尺寸和公差,实现稳健设计,描述物理系统行为或确定理想的制造设置。 收起阅读 »
1. 使用可视化识别产品中的问题。在可能的情况下,收集常用的数据并绘制成图表直方图、帕累托图、热图甚至相关图. Minitab的新图形生成器使您能够轻松地可视化您的数据,并看到您从未考虑过的可视化效果。
2. 使用过程分析工具识别问题。无论您是否已经识别出问题,过程分析工具都可以帮助您回顾过程,以识别失败的地方或改进的机会。故障模式和影响分析,也称为FMEAs,帮助您评估风险和流程图或流程图可以帮助你快速锁定需要关注的区域。
3. 使用控制图评估过程稳定性。机械工程师应该监控他们的过程,以确保质量和一致性。有许多统计工具,如控制图和能力分析这有助于机械工程师监控过程中的变化,并确定过程是否会生产出符合要求规格的产品。Minitab支持的实时SPC提供即时警报和分析,以确保流程稳定、高效和有能力。
4. 使用产品开发工具和方法设计和开发原型。在使用CAD系统之前,你应该使用许多产品开发工具。将产品推向市场需要对客户的需求和需求有充分的了解,以及严格的方法。学习如何使用决策矩阵工具就像质量矩阵或Pugh矩阵或向这家医疗设备制造商学习,他们利用客户总结和Kano模型的声音,以迅雷不及掩耳之势将新产品推向市场。如果您有兴趣了解产品开发方法(以及更多!),请查看我们的结构化问题解决方法周期表.
5. 利用实验设计。实验设计(DOE)是一种系统的、严谨的解决问题的方法,它确保产生有效的、可辩护的和可支持的结论。它可以有效地解决一般问题,以及改善或优化产品设计和制造过程。机械工程师可以使用DOE来:确定适当的设计尺寸和公差,实现稳健设计,描述物理系统行为或确定理想的制造设置。 收起阅读 »
用DOE烤出更好的饼干
当他们最喜欢的糖曲奇配方制作的曲奇在烘焙后无法保持节日形状时,一个有质量意识的面包师该怎么办呢?当然是运行实验设计(DOE)啦!
从部分因子实验开始
莫德·沃德是Minitab的一名狂热的面包师和平面设计师,他使用实验设计(DOE)工具Minitab统计软件去弄清她糖饼干造型的失礼之处。
在Minitab出色的技术支持团队的帮助下,Maud设计了一个实验,让她能够筛选许多因素,确定哪些是最重要的,然后调整她的过程,以获得她想要的结果——在这种情况下,制作烘烤后保持形状的饼干。
她决定经营一家部分因子实验,一类因子设计,可让您快速、经济地确定过程中最重要的因素。
莫德的实验要求她进行八次运行(或批次饼干)来评估六个因素,每个因素都在两个水平上进行测试:
· 烤箱温度:325华氏度或375华氏度
· 鸡蛋数量:1或2
· 通用面粉:9盎司。或者13.5盎司。
· 小苏打:0.5或1茶匙
· 酒石霜:0.5或1茶匙
· 揉搓和切割后冷却面团:是或否
为了确保面团厚度一致,莫德用木条来防止她的擀面杖将面团压得比1/4英寸(6.35毫米)更薄。然后,她随机地将饼干放置在烤板上,以尽量减少烘烤过程中的不当影响或无意偏差,并在烘烤中途将烤板旋转180度。
因为实验中使用了两种烤箱温度,所以烘烤时间因试验而异。每次试验的实际烹饪时间记录在试验说明表上。
每次试验包括烘烤两托盘饼干。当它们从烤箱中出来时,莫德测量了两个托盘中每种形状的两个样品,以查看整体高度、选定的宽度尺寸或厚度是否有变化。这些尺寸记录在预先打印的表格上,表格上标明了试验编号、试验数据、宽度和高度。莫德计算了她的饼干形状的平均值和标准偏差,然后使用Minitab统计软件来分析数据。
获得美味的DOE结果
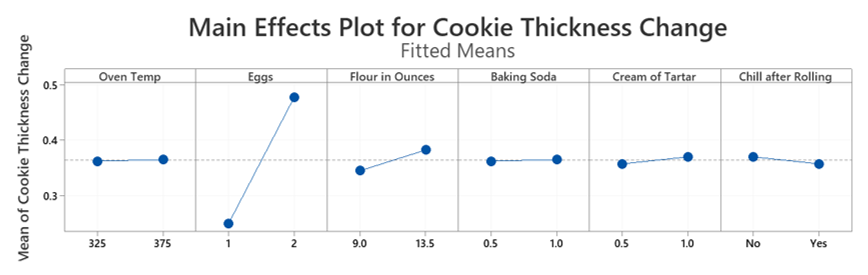
在Minitab中进行的高度和宽度测量的分析显示,面粉是饼干扩散的驱动因素。莫德说:“在每一个例子中,面粉量越多,从原始尺寸开始的扩散就越少。”“对饼干厚度的影响主要受面粉和面糊中鸡蛋数量的影响。用两个鸡蛋比只用一个鸡蛋产生的上升更多。”
莫德随后使用Minitab创建了主要效果图,检查一个或多个因素的水平平均值之间的差异。
最后,响应优化器帮助确定导致最小扩散和最大高度的因子设置。
由于Minitab和技术支持团队的帮助,Maud现在相信她设计和分析的实验将在这个假期和未来的更多假期中带来更好的饼干。对我来说,听起来像完美的,美味的结果! 收起阅读 »
从部分因子实验开始
莫德·沃德是Minitab的一名狂热的面包师和平面设计师,他使用实验设计(DOE)工具Minitab统计软件去弄清她糖饼干造型的失礼之处。
在Minitab出色的技术支持团队的帮助下,Maud设计了一个实验,让她能够筛选许多因素,确定哪些是最重要的,然后调整她的过程,以获得她想要的结果——在这种情况下,制作烘烤后保持形状的饼干。
她决定经营一家部分因子实验,一类因子设计,可让您快速、经济地确定过程中最重要的因素。
莫德的实验要求她进行八次运行(或批次饼干)来评估六个因素,每个因素都在两个水平上进行测试:
· 烤箱温度:325华氏度或375华氏度
· 鸡蛋数量:1或2
· 通用面粉:9盎司。或者13.5盎司。
· 小苏打:0.5或1茶匙
· 酒石霜:0.5或1茶匙
· 揉搓和切割后冷却面团:是或否
为了确保面团厚度一致,莫德用木条来防止她的擀面杖将面团压得比1/4英寸(6.35毫米)更薄。然后,她随机地将饼干放置在烤板上,以尽量减少烘烤过程中的不当影响或无意偏差,并在烘烤中途将烤板旋转180度。
因为实验中使用了两种烤箱温度,所以烘烤时间因试验而异。每次试验的实际烹饪时间记录在试验说明表上。
每次试验包括烘烤两托盘饼干。当它们从烤箱中出来时,莫德测量了两个托盘中每种形状的两个样品,以查看整体高度、选定的宽度尺寸或厚度是否有变化。这些尺寸记录在预先打印的表格上,表格上标明了试验编号、试验数据、宽度和高度。莫德计算了她的饼干形状的平均值和标准偏差,然后使用Minitab统计软件来分析数据。
获得美味的DOE结果
在Minitab中进行的高度和宽度测量的分析显示,面粉是饼干扩散的驱动因素。莫德说:“在每一个例子中,面粉量越多,从原始尺寸开始的扩散就越少。”“对饼干厚度的影响主要受面粉和面糊中鸡蛋数量的影响。用两个鸡蛋比只用一个鸡蛋产生的上升更多。”
莫德随后使用Minitab创建了主要效果图,检查一个或多个因素的水平平均值之间的差异。
最后,响应优化器帮助确定导致最小扩散和最大高度的因子设置。
由于Minitab和技术支持团队的帮助,Maud现在相信她设计和分析的实验将在这个假期和未来的更多假期中带来更好的饼干。对我来说,听起来像完美的,美味的结果! 收起阅读 »
DOE之优化烧烤口味01-创建建模设计
概述
试验设计(DOE)具有难度,但在某种程度上,这种统计方法又非常有用。虽然很容易掌握基本思想:从最少的实验运行中获取最大量的信息 。但这个工具的实际应用会很令人头疼,即使你是试验设计的长期使用者。基于DOE是一个非常强大且有用的工具,因此我们在Minitab协助菜单中添加了一个DOE工具,使更多人能够更方便地使用设计试验。我将向您展示如何使用协助菜单中的DOE工具来优化您的烧烤味道。
两种试验设计:筛选和优化
要使用“协助”创建试验设计,请打开Minitab并选择“ 协助”>“DOE”>“计划和创建”。您将看到一个决策树,通过在筛选设计和建模设计之间进行选择,帮助您采用顺序方法进行试验过程。
如果您需要考虑很多潜在因子 并且想要确定哪些是重要的,筛选设计很重要。协助将指导您完成测试和分析6到15个因子的主要影响的过程,并确定对响应影响最大的因子。一旦确定了关键因子,就可以使用建模设计。选择此选项,协助将指导您完成分析2到5个关键因子,并帮助您找到流程的最佳设置。
即使您是分析设计实验的老手,您也可以使用协助创建设计,因为协助可以让您为每个实验运行打印出易于使用的数据收集表单。收集并输入数据后,还可以使用通过统计> DOE菜单提供Minitab 核心DOE工具分析在协助菜单中创建的设计 。
创建建模设计优化烧烤口味
对于烧烤,没有那么多变量需要考虑,因此我们将使用协助来创建一个可以优化我们烧烤过程的建模设计。选择协助> DOE> 计划优化试验,然后单击“创建建模设计”按钮。
Minitab提供了一个易于理解的对话框; 我们需要做的只是填写。
首先,我们输入响应的名称和实验的目标。这里的响应变量是“口味”,目标是“最大化响应”。接下来,我们输入我们的因子。我们将研究三个关键变量:
串数,连续变量,低水平为1,高水平为3。
烤架类型,类别变量,低水平为气体,高水平为木炭。
调味料的类型,类别变量,低水平是盐胡椒,高水平为蒙特利尔牛排。
如果我们想要,我们可以选择超过1个实验仿行。仿行只是一组完整的实验运行,因此如果我们进行3次仿行,我们将重复完整实验三次。但是,由于这个实验有16次运行,我们的预算有限制,我们将坚持一次仿行。 当我们单击“确定”时,“协助”会首先询问是否要打印出此实验的数据收集表单:
选择是,您可以打印一个表单,列出每个运行,变量和设置,以及空的响应列。或者,您可以在协助创建的工作表中记录每次运行的结果。但是,使用打印的数据收集表单可以更容易地跟踪您在试验中的位置,以及每次运行时您的因子设置应该是什么。
如果您已将Minitab中的协助用于其他方法(例如:控制图、过程能力分析),您就会知道它旨在揭开您的分析的神秘面纱并使其易于理解。在您创建实验时,智能协助菜单会为您提供报告卡和摘要报告,说明DOE的步骤和重要注意事项,以及您的目标摘要和分析将显示的内容。 收起阅读 »
试验设计(DOE)具有难度,但在某种程度上,这种统计方法又非常有用。虽然很容易掌握基本思想:从最少的实验运行中获取最大量的信息 。但这个工具的实际应用会很令人头疼,即使你是试验设计的长期使用者。基于DOE是一个非常强大且有用的工具,因此我们在Minitab协助菜单中添加了一个DOE工具,使更多人能够更方便地使用设计试验。我将向您展示如何使用协助菜单中的DOE工具来优化您的烧烤味道。
两种试验设计:筛选和优化
要使用“协助”创建试验设计,请打开Minitab并选择“ 协助”>“DOE”>“计划和创建”。您将看到一个决策树,通过在筛选设计和建模设计之间进行选择,帮助您采用顺序方法进行试验过程。
如果您需要考虑很多潜在因子 并且想要确定哪些是重要的,筛选设计很重要。协助将指导您完成测试和分析6到15个因子的主要影响的过程,并确定对响应影响最大的因子。一旦确定了关键因子,就可以使用建模设计。选择此选项,协助将指导您完成分析2到5个关键因子,并帮助您找到流程的最佳设置。
即使您是分析设计实验的老手,您也可以使用协助创建设计,因为协助可以让您为每个实验运行打印出易于使用的数据收集表单。收集并输入数据后,还可以使用通过统计> DOE菜单提供Minitab 核心DOE工具分析在协助菜单中创建的设计 。
创建建模设计优化烧烤口味
对于烧烤,没有那么多变量需要考虑,因此我们将使用协助来创建一个可以优化我们烧烤过程的建模设计。选择协助> DOE> 计划优化试验,然后单击“创建建模设计”按钮。
Minitab提供了一个易于理解的对话框; 我们需要做的只是填写。
首先,我们输入响应的名称和实验的目标。这里的响应变量是“口味”,目标是“最大化响应”。接下来,我们输入我们的因子。我们将研究三个关键变量:
串数,连续变量,低水平为1,高水平为3。
烤架类型,类别变量,低水平为气体,高水平为木炭。
调味料的类型,类别变量,低水平是盐胡椒,高水平为蒙特利尔牛排。
如果我们想要,我们可以选择超过1个实验仿行。仿行只是一组完整的实验运行,因此如果我们进行3次仿行,我们将重复完整实验三次。但是,由于这个实验有16次运行,我们的预算有限制,我们将坚持一次仿行。 当我们单击“确定”时,“协助”会首先询问是否要打印出此实验的数据收集表单:
选择是,您可以打印一个表单,列出每个运行,变量和设置,以及空的响应列。或者,您可以在协助创建的工作表中记录每次运行的结果。但是,使用打印的数据收集表单可以更容易地跟踪您在试验中的位置,以及每次运行时您的因子设置应该是什么。
如果您已将Minitab中的协助用于其他方法(例如:控制图、过程能力分析),您就会知道它旨在揭开您的分析的神秘面纱并使其易于理解。在您创建实验时,智能协助菜单会为您提供报告卡和摘要报告,说明DOE的步骤和重要注意事项,以及您的目标摘要和分析将显示的内容。 收起阅读 »
优秀试验设计的8个专业建议
如果您的工作涉及质量改进,那么您至少听说过实验设计 (DOE)。您可能知道这是优化和改进流程的最有效方式。但我们中的许多人发现 DOE 令人生畏,尤其是如果它不是我们经常使用的工具。您如何选择合适的设计,并确保您拥有正确数量的因素和水平?收集数据后,如何为分析选择合适的模型?
开始使用 DOE 的一种方法是 Minitab Statistical Software 中的助手。当您有许多要评估的因素时,助手将引导您完成DOE以确定哪些因素最重要(筛选设计)。然后,助手可以指导您完成设计实验,以微调重要因素以获得最大影响(优化设计)。
如果您可以轻松跳过助手,但对于您是否以正确的方式接近 DOE 仍有一些疑问,请考虑 Minitab 技术培训师提供的以下提示。这些资深人士在与 Minitab 客户合作期间以及在成为 Minitab 培训师之前的职业生涯中,都进行了大量设计实验。
1. 通过探索性运行确定正确的变量空间。
在进行主要实验之前执行探索性运行可以帮助您在性能从好到差时识别过程的设置。这可以帮助您确定进行实验的可变空间,从而产生最有益的结果。
2. 传播控制贯穿整个实验以测量过程稳定性。
由于中心点运行通常是接近正常的操作条件,它们可以作为检查过程性能的控制。通过在设计中均匀地间隔中心点,这些观察结果可作为实验期间过程稳定性或缺乏稳定性的指标。
3. 找出帕累托分析的最大问题。
产品负载或缺陷级别的帕累托图可以帮助您确定要解决的问题,从而为您的业务带来最高回报。关注具有高业务影响的问题,通过在所有潜在改进项目中提高其优先级来提高对实验的支持。
4.通过扩大输入设置范围来提高功率。
测试物理上可能的最大范围的输入变量设置。即使您认为它们远离“最佳位置”,该技术也将允许您使用实验来了解您的过程,以便您找到最佳设置。
5. 分馏以节省运行,专注于分辨率 V 设计。
在许多情况下,选择具有全因子 ½ 或 ¼ 游程的设计是有益的。即使效应可能相互混淆或混淆,Resolution V 设计可最大限度地减少这种混淆的影响,从而使您能够估计所有主要效应和双向交互作用。进行更少的运行可以节省资金并保持较低的实验成本。
6. 通过重复提高实验的效力。
功效是检测到对响应的影响(如果存在该影响)的概率。重复次数会影响实验的功效。为了增加您成功识别影响您的响应的输入的机会,请在您的实验中添加重复以增加其功效。
7. 通过使用量化措施来提高你的反应能力。
减少缺陷是大多数实验的主要目标,因此缺陷计数通常用作响应是有道理的。但是缺陷计数是一种非常昂贵且反应迟钝的输出来衡量。相反,请尝试测量与您的缺陷级别相关的定量指标。这样做可以显着减少样本量并提高实验的能力。
8. 研究所有感兴趣的变量和所有关键响应。
因子设计让您可以采用全面的方法来研究所有潜在的输入变量。从实验中删除一个因素会将您确定其重要性的机会减少到零。借助Minitab 等统计软件中的可用工具,您不应该让对复杂性的恐惧导致您忽略可能重要的输入变量。 收起阅读 »
开始使用 DOE 的一种方法是 Minitab Statistical Software 中的助手。当您有许多要评估的因素时,助手将引导您完成DOE以确定哪些因素最重要(筛选设计)。然后,助手可以指导您完成设计实验,以微调重要因素以获得最大影响(优化设计)。
如果您可以轻松跳过助手,但对于您是否以正确的方式接近 DOE 仍有一些疑问,请考虑 Minitab 技术培训师提供的以下提示。这些资深人士在与 Minitab 客户合作期间以及在成为 Minitab 培训师之前的职业生涯中,都进行了大量设计实验。
1. 通过探索性运行确定正确的变量空间。
在进行主要实验之前执行探索性运行可以帮助您在性能从好到差时识别过程的设置。这可以帮助您确定进行实验的可变空间,从而产生最有益的结果。
2. 传播控制贯穿整个实验以测量过程稳定性。
由于中心点运行通常是接近正常的操作条件,它们可以作为检查过程性能的控制。通过在设计中均匀地间隔中心点,这些观察结果可作为实验期间过程稳定性或缺乏稳定性的指标。
3. 找出帕累托分析的最大问题。
产品负载或缺陷级别的帕累托图可以帮助您确定要解决的问题,从而为您的业务带来最高回报。关注具有高业务影响的问题,通过在所有潜在改进项目中提高其优先级来提高对实验的支持。
4.通过扩大输入设置范围来提高功率。
测试物理上可能的最大范围的输入变量设置。即使您认为它们远离“最佳位置”,该技术也将允许您使用实验来了解您的过程,以便您找到最佳设置。
5. 分馏以节省运行,专注于分辨率 V 设计。
在许多情况下,选择具有全因子 ½ 或 ¼ 游程的设计是有益的。即使效应可能相互混淆或混淆,Resolution V 设计可最大限度地减少这种混淆的影响,从而使您能够估计所有主要效应和双向交互作用。进行更少的运行可以节省资金并保持较低的实验成本。
6. 通过重复提高实验的效力。
功效是检测到对响应的影响(如果存在该影响)的概率。重复次数会影响实验的功效。为了增加您成功识别影响您的响应的输入的机会,请在您的实验中添加重复以增加其功效。
7. 通过使用量化措施来提高你的反应能力。
减少缺陷是大多数实验的主要目标,因此缺陷计数通常用作响应是有道理的。但是缺陷计数是一种非常昂贵且反应迟钝的输出来衡量。相反,请尝试测量与您的缺陷级别相关的定量指标。这样做可以显着减少样本量并提高实验的能力。
8. 研究所有感兴趣的变量和所有关键响应。
因子设计让您可以采用全面的方法来研究所有潜在的输入变量。从实验中删除一个因素会将您确定其重要性的机会减少到零。借助Minitab 等统计软件中的可用工具,您不应该让对复杂性的恐惧导致您忽略可能重要的输入变量。 收起阅读 »
二值响应DOE-汽车挡风玻璃断裂问题
二值响应DOE
传统实验设计的因子类型可以是连续型的也可以是文本型的,而响应变量都是连续型的,如我们想考察材料类型、注塑压力、注塑温度、冷却温度对绝缘强度的影响。现在Minitab 21中新增了二值响应DOE的功能,所谓二值响应就是结果只有两种可能,是/否,好/坏,合格/不合格。二值响应DOE,您可以在Minitab 21的以下分析中找到。
筛选设计
因子设计
响应曲面设计
问题背景
一家汽车制造商想观察由于外来物质损害挡风玻璃所产生的裂纹,他们考虑了三个因子:外来粒子的速度、粒子重量和玻璃供应商。
A: 颗粒的速度(mph),低水平:50, 高水平:60
B: 颗粒的重量(gram),低水平:20, 高水平:40
C: 挡风玻璃的供应商:低水平:A,高水平:B
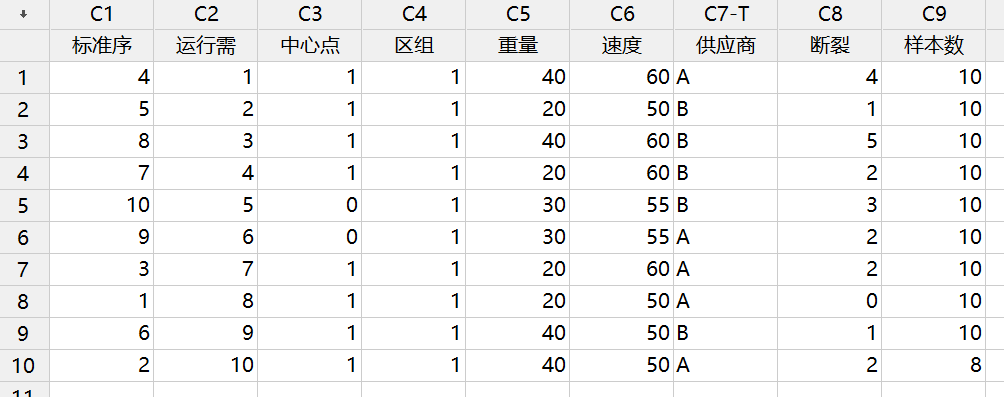
数据收集
在一个特殊的设计实验房间里,一种颗粒被射向固定于20英尺远的挡风玻璃,一个检验员记录挡风玻璃是否产生裂纹,每种挡风玻璃只使用一次。制造商具有进行对100种挡风玻璃进行实验的资金、时间和材料,允许研究者试验10种挡风玻璃的样本大小。每8个因子的组合和两个中心点。然而,从供应商A只能获得48种挡风玻璃,因此,最后一轮实验只包括8种挡风玻璃样本。
分析二值DOE
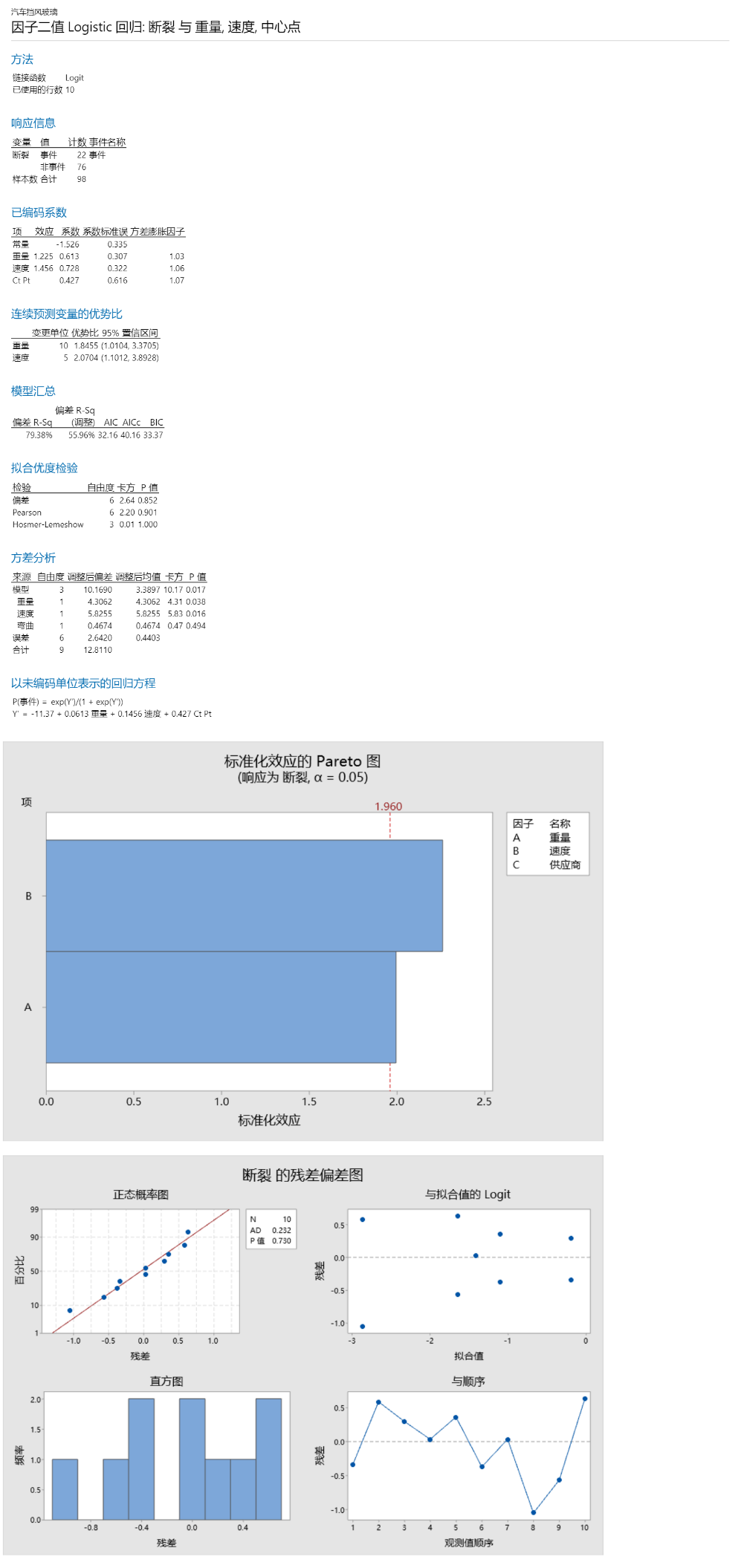
在Minitab 21的二值响应DOE分析种,除了主对话框跟经典实验设计有比较大区别以外,其他选项,比如“项”、“图形”中的设置是没有差别的。
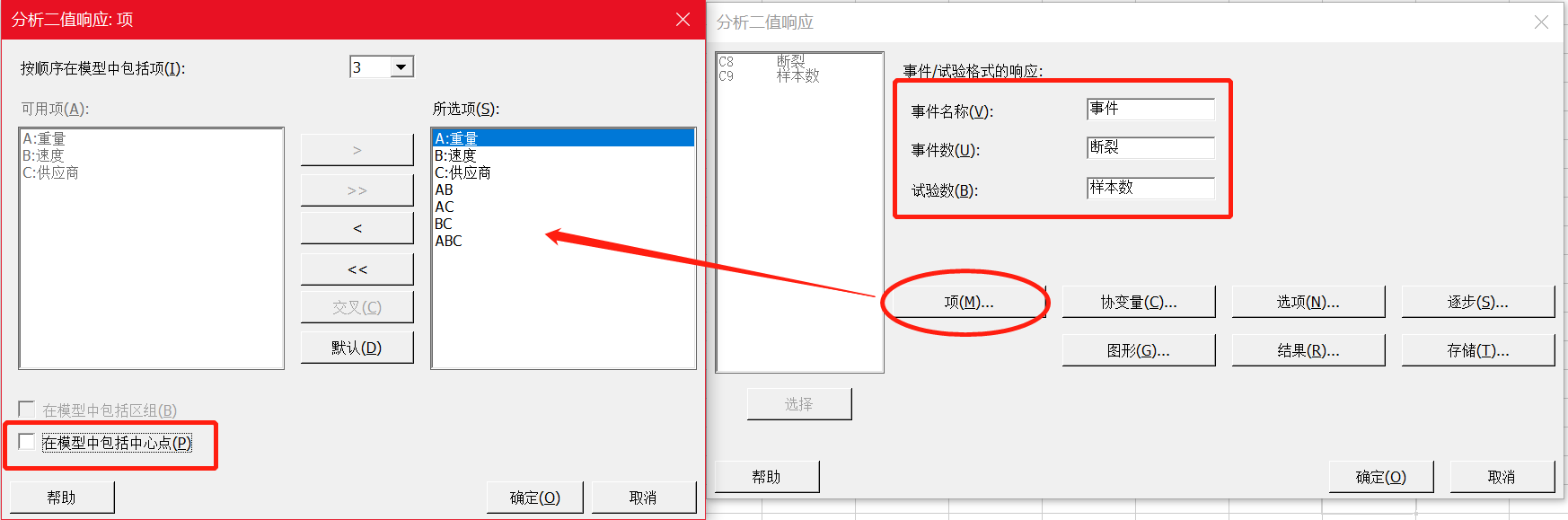
在“项”中,我们第一次拟合模型时,把所有的项都考虑进来(在下面分析中有一个陷阱,请注意哦)。
所有对话框点击确定后,得到如下结果。
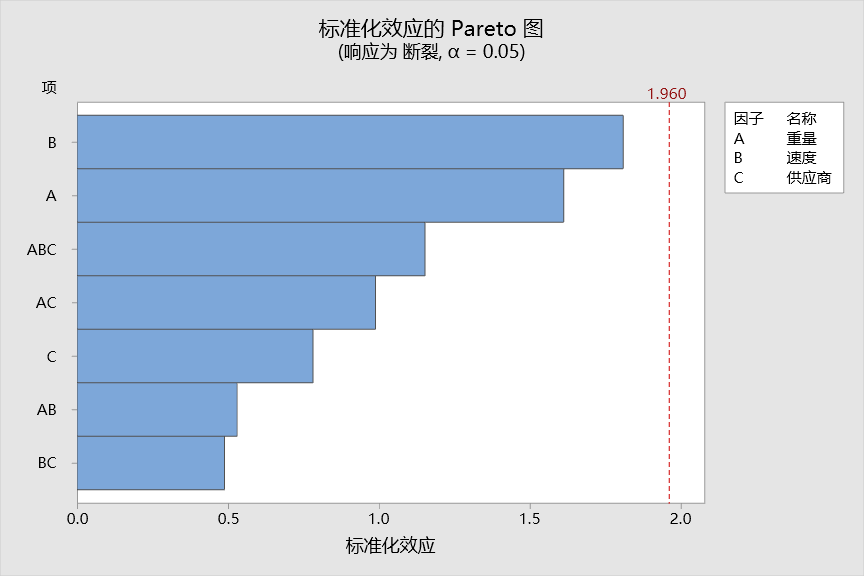
注意:当我们把所有项都加入到模型中,这时候我们可以看到没有显著的项,此时不要急着下结论。这时候一般的做法是先删除高阶交互作用项。
删除三阶交互作用项和所有二阶交互作用项以后,我们可以看到这时候A和B变成显著的了,C仍然不显著,在下一步优化中需要删除掉。我们得到以下的最终结果。
优势比
仅当您为具有二元响应的模型选择 logit 链接函数时才提供优势比。在这种情况下,优势比可用于解释预测变量与响应之间的关系。
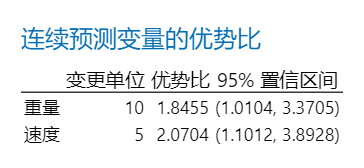
连续预测变量的优势比:优势比大于 1 表示在预测变量越大,事件发生的几率越大。优势比小于 1 表示预测变量越大,事件发生的几率越小。在当前结果中,该模型使用颗粒的重量水平来预测汽车挡风玻璃是否断裂。在此示例中,挡风玻璃断裂为“事件”。每颗粒的重量为10gram,因此研究人员使用10gram作为一个单位变化。优势比约为1.8455。颗粒重量每增加一个单位,挡风玻璃断裂的比率就增加约1.8455倍。颗粒速度的优势比解释结果一样,不再赘述。
类别预测变量(当前结果没有)的优势比:对于类别预测变量,优势比可以比较事件在两个不同的预测变量水平发生的几率。Minitab 通过在水平 A 和水平 B 这两列中列出水平来设置比较。水平 B 是因子的参考水平。优势比大于 1 表示事件在水平 A 下发生的几率大。优势比小于 1 表示事件在水平 A 下发生的几率小。
结论
在Minitab 21中有了二值响应DOE分析,扩展了DOE的功能。当然,在实验设计中我们除了遇到二值响应DOE外,可能还会遇到残差分析有问题需要对响应变量做变换的DOE分析、带区组的实验设计分析等比较复杂的DOE问题。我们将在后续为大家一一分享,如果您还没有使用过Minitab 21,可以登陆Minitab官网下载30天免费试用版哦! 收起阅读 »
传统实验设计的因子类型可以是连续型的也可以是文本型的,而响应变量都是连续型的,如我们想考察材料类型、注塑压力、注塑温度、冷却温度对绝缘强度的影响。现在Minitab 21中新增了二值响应DOE的功能,所谓二值响应就是结果只有两种可能,是/否,好/坏,合格/不合格。二值响应DOE,您可以在Minitab 21的以下分析中找到。
筛选设计
因子设计
响应曲面设计
问题背景
一家汽车制造商想观察由于外来物质损害挡风玻璃所产生的裂纹,他们考虑了三个因子:外来粒子的速度、粒子重量和玻璃供应商。
A: 颗粒的速度(mph),低水平:50, 高水平:60
B: 颗粒的重量(gram),低水平:20, 高水平:40
C: 挡风玻璃的供应商:低水平:A,高水平:B
数据收集
在一个特殊的设计实验房间里,一种颗粒被射向固定于20英尺远的挡风玻璃,一个检验员记录挡风玻璃是否产生裂纹,每种挡风玻璃只使用一次。制造商具有进行对100种挡风玻璃进行实验的资金、时间和材料,允许研究者试验10种挡风玻璃的样本大小。每8个因子的组合和两个中心点。然而,从供应商A只能获得48种挡风玻璃,因此,最后一轮实验只包括8种挡风玻璃样本。
分析二值DOE
在Minitab 21的二值响应DOE分析种,除了主对话框跟经典实验设计有比较大区别以外,其他选项,比如“项”、“图形”中的设置是没有差别的。
在“项”中,我们第一次拟合模型时,把所有的项都考虑进来(在下面分析中有一个陷阱,请注意哦)。
所有对话框点击确定后,得到如下结果。
注意:当我们把所有项都加入到模型中,这时候我们可以看到没有显著的项,此时不要急着下结论。这时候一般的做法是先删除高阶交互作用项。
删除三阶交互作用项和所有二阶交互作用项以后,我们可以看到这时候A和B变成显著的了,C仍然不显著,在下一步优化中需要删除掉。我们得到以下的最终结果。
优势比
仅当您为具有二元响应的模型选择 logit 链接函数时才提供优势比。在这种情况下,优势比可用于解释预测变量与响应之间的关系。
连续预测变量的优势比:优势比大于 1 表示在预测变量越大,事件发生的几率越大。优势比小于 1 表示预测变量越大,事件发生的几率越小。在当前结果中,该模型使用颗粒的重量水平来预测汽车挡风玻璃是否断裂。在此示例中,挡风玻璃断裂为“事件”。每颗粒的重量为10gram,因此研究人员使用10gram作为一个单位变化。优势比约为1.8455。颗粒重量每增加一个单位,挡风玻璃断裂的比率就增加约1.8455倍。颗粒速度的优势比解释结果一样,不再赘述。
类别预测变量(当前结果没有)的优势比:对于类别预测变量,优势比可以比较事件在两个不同的预测变量水平发生的几率。Minitab 通过在水平 A 和水平 B 这两列中列出水平来设置比较。水平 B 是因子的参考水平。优势比大于 1 表示事件在水平 A 下发生的几率大。优势比小于 1 表示事件在水平 A 下发生的几率小。
结论
在Minitab 21中有了二值响应DOE分析,扩展了DOE的功能。当然,在实验设计中我们除了遇到二值响应DOE外,可能还会遇到残差分析有问题需要对响应变量做变换的DOE分析、带区组的实验设计分析等比较复杂的DOE问题。我们将在后续为大家一一分享,如果您还没有使用过Minitab 21,可以登陆Minitab官网下载30天免费试用版哦! 收起阅读 »
实验设计中如何判因子之间的断嵌套与交叉问题
是交叉还是嵌套 (引用百度文库资料整理)
例子一:考虑车工车间在生产标准螺钉时的直径波动过大问题。
随机选取3 名工人,各自分别加工出4 颗螺钉,然后在每颗螺钉的根部随机选取两个相互垂直的方向,分别测量其直径,共得到24 颗数据。将"工人"这个因子记为因子A ,将 "螺钉" 这个因子记为因子 B ,那么, A 与 B 两个因子间是什么样的关系呢?
由于每个工人生产的4 颗螺钉,是分别附属于相应的工人的。 即使我们将这些螺钉都编号为 1 , 2 , 3 , 4 ,但是很明显,工人A 和工人B 之下的编号皆为1 的两颗螺钉并不是同一件东西。这时,称因子B "螺钉"是被因子A"工人"所嵌套着的 (Factor B is nested with factor A) 。很明显,此种情况下的两个因子所处的地位是不能被颠倒过来的。
然而,在实际情况中,两个因子间还可能存在另一种关系。例如,3 名工人轮流使用共同的4 台编了号的车床,每个工人都使用了车床 1, 2 , 3 , 4 ,这时,工人A 和工人B 之下的编号都为 1 的两台车床是同一件东西。 而且可以反过来说,每台车床都被3 名工人使用过。这时,称因子B "车床"是与因子A "工人"相交叉 (Factor B is crossed with factor A) 。很明显,如果这时 候说因子A"工人"与因子B "车床"相交叉也是同样的,它们的位置是可以颠倒过来的。这里要注意,单从树状图上是不能区分两个因子的关系是交叉还是嵌套的,只能从实际意义判断之。
例子二:选取3 名工人,让他们使用编好号的 4 台车床,按随机顺序各自分别加工出 3 根立轴。
若将与因子A (工人) 及搭配的因子B ( 车床) 的每台车床编好号,则可以发现,因子A (工人)与因子B (车床) 间的关系是交叉关系。 注意,它们两因子间可以颠倒顺序,即可以反过来说,因子B (车床) 的每个值也都与因 子A (工人) 的每个值搭配过。
如果车床不是固定的编号的车床,而是每个工人各自有自己固有的4 台车床,这时因子A (工人)与因子 B(车床) 间的关系就不再是交叉关系,而是嵌套关系了。
例子三: 现在讨论三因子问题。由于不能将立轴(半成品尺寸/材质等等)之间的变异看成随机误差,因而要求将立轴之间的变异也看成因子,即形成三因子问题。这里3 名工人 (因子A) ,分别使用己选好并编了号的4 台车床(因子B),各自分别加工出3 根立轴 (因子C),然后对每根" 立轴测两次直径(误差)。由于因子B 的4 台车床是固定的,所以工人(因子A) 与车床 (因子B) 之间是交叉关系,而立轴 (因子C) 则是被A 与B 所嵌套的,即三因子是先交叉后嵌套的关系。
如果,将例子10-3 的安排稍加调整: 3 名工人 (因子A) ,分别使用自己固定的4 台车床(因子B),各自分别加工出3 根立轴 (因子C)。,这时因子间的关系就会发生变化。这时B被A 所嵌套, C 被A,B 所嵌套,这种关系也被称为全嵌套关系 (fully nested) 。
实际问题中可能有多种结构,但仔细分析它们的数据就可以发现,因子间的关系无非 是嵌套或交叉这两种基本类型。有时在实际问题中可能遇到的是因子个数较多,关系较复杂,这时需要仔细分析处理。
收起阅读 »
例子一:考虑车工车间在生产标准螺钉时的直径波动过大问题。
随机选取3 名工人,各自分别加工出4 颗螺钉,然后在每颗螺钉的根部随机选取两个相互垂直的方向,分别测量其直径,共得到24 颗数据。将"工人"这个因子记为因子A ,将 "螺钉" 这个因子记为因子 B ,那么, A 与 B 两个因子间是什么样的关系呢?
由于每个工人生产的4 颗螺钉,是分别附属于相应的工人的。 即使我们将这些螺钉都编号为 1 , 2 , 3 , 4 ,但是很明显,工人A 和工人B 之下的编号皆为1 的两颗螺钉并不是同一件东西。这时,称因子B "螺钉"是被因子A"工人"所嵌套着的 (Factor B is nested with factor A) 。很明显,此种情况下的两个因子所处的地位是不能被颠倒过来的。
然而,在实际情况中,两个因子间还可能存在另一种关系。例如,3 名工人轮流使用共同的4 台编了号的车床,每个工人都使用了车床 1, 2 , 3 , 4 ,这时,工人A 和工人B 之下的编号都为 1 的两台车床是同一件东西。 而且可以反过来说,每台车床都被3 名工人使用过。这时,称因子B "车床"是与因子A "工人"相交叉 (Factor B is crossed with factor A) 。很明显,如果这时 候说因子A"工人"与因子B "车床"相交叉也是同样的,它们的位置是可以颠倒过来的。这里要注意,单从树状图上是不能区分两个因子的关系是交叉还是嵌套的,只能从实际意义判断之。
例子二:选取3 名工人,让他们使用编好号的 4 台车床,按随机顺序各自分别加工出 3 根立轴。
若将与因子A (工人) 及搭配的因子B ( 车床) 的每台车床编好号,则可以发现,因子A (工人)与因子B (车床) 间的关系是交叉关系。 注意,它们两因子间可以颠倒顺序,即可以反过来说,因子B (车床) 的每个值也都与因 子A (工人) 的每个值搭配过。
如果车床不是固定的编号的车床,而是每个工人各自有自己固有的4 台车床,这时因子A (工人)与因子 B(车床) 间的关系就不再是交叉关系,而是嵌套关系了。
例子三: 现在讨论三因子问题。由于不能将立轴(半成品尺寸/材质等等)之间的变异看成随机误差,因而要求将立轴之间的变异也看成因子,即形成三因子问题。这里3 名工人 (因子A) ,分别使用己选好并编了号的4 台车床(因子B),各自分别加工出3 根立轴 (因子C),然后对每根" 立轴测两次直径(误差)。由于因子B 的4 台车床是固定的,所以工人(因子A) 与车床 (因子B) 之间是交叉关系,而立轴 (因子C) 则是被A 与B 所嵌套的,即三因子是先交叉后嵌套的关系。
如果,将例子10-3 的安排稍加调整: 3 名工人 (因子A) ,分别使用自己固定的4 台车床(因子B),各自分别加工出3 根立轴 (因子C)。,这时因子间的关系就会发生变化。这时B被A 所嵌套, C 被A,B 所嵌套,这种关系也被称为全嵌套关系 (fully nested) 。
实际问题中可能有多种结构,但仔细分析它们的数据就可以发现,因子间的关系无非 是嵌套或交叉这两种基本类型。有时在实际问题中可能遇到的是因子个数较多,关系较复杂,这时需要仔细分析处理。
收起阅读 »
QRQC信息化解决方案
QRQC全名质量问题快速反馈和质量问题解决。90年代由日本尼桑创建,2002被法雷奥采用,并在众多著名企业得到推广,目前QRQC正成为汽车行业质量标准之一。QRQC思想力图从行为,工具,组织三个方面打造质量文化。本方案包含三个模块,快反系统+问题解决+谢宁方法工具集,着力打造质量管理透明化工厂。 收起阅读 »
正交设计的交互效应:新的思维方法
由于传统DOE和田口方法都有软件可轻松使用,初学者还要理解其内在的深刻思想。
有学者认为正交试验是一种认知和思维方法,其中最重要显示了复杂隐藏的交互效应。
传统的线性思维方法:
把整体作用看作是其部分作用之和,但是交互效应是一加一不等于二!
数学家尽可能把非线性问题转换成线性,是为了计算方便,数学模型变简洁。而人对复杂的客观世界用僵化线性思维方式,就会有片面性,甚至歪曲事物真实面貌。
笔者看到多元交互作用概念已经用于社会科学的文献,从宏观角度分析,在社会科学上应用比工程上应用更有深刻意义。
正如马克思所言:
任何一门科学只有充分利用了数学时,才能真正达到完善地步。
马克思写过微积分方面的论文,所以他所指的数学不会是算术水平。
但目前在社会科学中用百分比、平均数等算术概念太多。比如在定性分析时常会用非黑即白绝对性思维方法,而不是用模糊数学隶属度来度量。对未发生的决策常用肯定性的判定,而不是把思维因子处于0和1之间的概率思维方法。传统思维在博弈中认为只有非赢即输的结果,实际双方理智决策可双赢。
用交互效应概念可对某些社会问题有新的认识。
B0X戏称公鸡和母鸡关在一个笼子生出的小鸡就是交互效应。如公鸡母鸡关在独立的笼子里就生不出小鸡。
使人联想到贬义的剩余价值问题。
如雇主比作公鸡(或母鸡)、雇员比作母鸡(或公鸡),协作后产生的增值剩余价值比作小鸡。
传统说法雇主获得剩余价值就是剥削,社会主义市场经济现已淡化了,但未正名。因为非囯有经济对就业、产出、出口贡献远大于国有经济。
无论是雇主或雇员,如两者独立或缺一,就不会产生剩余价值。如两者对抗,产生负面交互效应,雇主破产、雇员下岗。
有的文献对交互效应的相关变量还分割为关键自变量和调节变量,如用条件效应解释交互效应,这二者可互换的。比如决定青铜强度的关键是铜和锡的比例问题,不必纠结銅贡献大还是锡贡献大。
正交试验中交互效应概念,不仅是统计学的概念,而且是认识客观世界多因子之间复杂纠葛的新概念。
收起阅读 »
直积法和一表法本质差异
田口方法噪声因子定义是不可控的,但为了检验可控因子组合的抗噪性,人为设定上下限水平。
比如上限“十”,实际是有一定波动幅度的,即是随机变量。所以内表每一个组合至少和上限试验2次,而且不能同期试验,次序随机化。
而一表法减少了次数,但把噪声因子水平常数化,对噪声干扰能力的估计会不足,稳健性设计的可信度降低了。 收起阅读 »
比如上限“十”,实际是有一定波动幅度的,即是随机变量。所以内表每一个组合至少和上限试验2次,而且不能同期试验,次序随机化。
而一表法减少了次数,但把噪声因子水平常数化,对噪声干扰能力的估计会不足,稳健性设计的可信度降低了。 收起阅读 »
用田口直积表理解稳健性设计 向DOE初学者进言(5)
BOX《试验应用统计》P338,清洁剂稳定性设计案例:4可控因子:2水平8次部分因析设计,3噪声因子:2水平4次部分因析设计,共32次不重复试验。原文称为裂区设计,这是典型田口直积表法。直积表也被称为乘积表,笔者认为乘积表更直观易理解。
但直积表常被人批评试验次数太多,直积表本质是每一个可控因子组合必需受过噪声因子组合的上下极限恶劣状态“压力”测试,其响应才是稳健的非实验室的数据。
有学者认为直积表可简化为一表法,即此案例成2水平7因子设计,这对稳健性设计是一种误解。
比如有一个2可控因子1噪声因子案例,一表法用2水平3因子因析设计8次试验,但每个可控因子组合只和上限噪声或和下限噪声各做4次试验。每个可控因子组合必须上下限噪声都做试验,即要再做8次,共16次试验。这样每一组可控因子组合在噪声上下限干扰下的均值和极差或样本方差是稳健性的指标。
而如有些学者用重复6次的样本方差作为离散性指标,但不是稳健性指标。而且重复多次试验总次数不比不重复的直积表少。
上述清洁剂案例旳噪声组合是省略的方法,忽略了部分噪声因子之间的交互效应。理想的噪声组合外表应用2水平3因子因析设计的8次试验,即需64次试验。
而传统D0E重视可控因子因析设计,而田口不少案例是噪声因子因析设计!?这就是稳健性设计的核心:可控因子可控,噪声因子不可控,只有通过试验才能知道噪声对响应的影响程度和可控因子和交互效应抑制噪声的效果。
收起阅读 »
自变量相关(共线性)问题 向DOE初学者进言(4)
当方便用软件处理DOE数据建数模后,
“我们往往可以非常自信地谈论总体估计的精确度。但是,我们对回归结果的信任程度取决于是否能够成功地处理以下常见问题:多元共线性、奇异值、非正态、异方差性以及非线性。”
单单就共线性问题,对寻找最优水平组合,也会带来判断困难。
《实用优选法》第3章望小型案例:A升温速度、B恒温温度、C恒温时间、D降温方式。
用极差法分析,对响应贡献大小排列:A>C>B>D。用部分正交试验:L9,3水平4因子。
9个结果中,C时间高水平6h组合,响应为1。
第2次正交试验之前,书中用“中心炮”和“两极炮”分析,都指向C时间8h和10h可能是最佳水平。但实际上第2次试验证明C时间3h或5h都能得到响应0。
原分析方向有误,笔者认为除部分正交试验信息不完备外,最重要的是A升温速度和C时间负相关,B恒温温度和C时间也负相关。
简易之:自变量之间相关不独立,有多种组合可达到最优(此案例响应为0)。
最后从经济角度,选C恒温时间3h的组合。
有的学者认为破解自变量相关的方法是去除一个自变量。
“一个常见的但往往容易被误用的解决共线性的方法是变量选择…用来将模型中回归因子减少至较低相关性的组合。”即逐步回归的方法, 但此案例,A和B都不能少。
统计假设最多的正态独立同分布,实际独立同分布是最基础性的约束。
也就是如不独立,不能用普通最小二乘法建数学模型,“对共线性的处理没有速效方法”。
比如SpC休哈特控制图,其中隐含前后工序独立,如不独立需用张公绪提出的SpD统计过程控制(选控图)。
多因子案例交互作用难避免,同样自变量之间相关也难避免。
所以高斯-马尔科夫七项假设中要求自变量之间没有完全的线性关系。
回归分析“尽管它是一件最常用的工具,但它同样有可能最容易被滥用的工具”
(《理解回归假设》序)
收起阅读 »
属非参数统计的部分正交试验 向DOE初学者进言(3)
属参数统计范畴的全因子析因设计,费歇在上世纪廿年代在农业DOE上已应用,但在工业上应用滞缓。原因是大于4因子工业案例众多,用全因子析因设计试验次数太多。而能大大减少试验次数的部分正交试验,其所谓主效应混杂交互效应,建数模困难。所以面对工业多因子案例两难局面,欧美学者裹足不前。
到40年代后期,纺织业专家田口玄一忽略部分正交试验的混杂问题,摆脱了非零交互作用必须甪全因子析因设计的束缚, 把部分正交试验用于工业多因子案例,在日本获得巨大成效。但欧美学者称田口方法是 “看不懂的天书”。
后来田口先生亲自在美国大企业,解决不少技术难题后,美国权威DOE文献都把田口稳健性设计列入章节:成功的实践更雄辩。
历史上,国内学者以参数统计理论观点,认为重复试验6次也是小样本,2水平4因子用8次试验样本太小,对其推断的可信度也曾持怀疑态度。北大学者在北京印染厂,现场参与的2水平7因子部分正交试验案例,仅用8次试验,成品率从32%提高到42%,反应时间缩短了近5小时。
实践促使反思理论,北大张里千认为部分正交试验属未知总体的非参数统计系统。
为了达到回归系数估计最小方差无偏估计,需适合高斯-马尔可夫7项假设;为了回归系数置信区间估计,还需正态分布假设…这都源于追求建回归方程的高目标。
依靠正交表的优良性,如仅以寻找最优水平组合,就可摆脱参数统计的约束。
张里千先生为田口方法找到了理论归属,也为各种非全因子析因设计各种DOE派别正了名。
并且说明正交表的均衝分散性、整齐可比性是小正交表用小样本产生高效能的关键:
如不删除惰性因子,网大易捕捉到冒尖区域;
因子水平间分散距离足够,系统性变异的信号能淹没随机性变异噪声;
每一水平参与试验次数相同,使每一组试验都有相同的统计解释力。
工业上百个参数案例不鲜见,用超饱和设计筛选、用各种非全因子析因设计是必要的,但非全因子析因设计信息不齐的软肋和追求建数学模型的高目标相悖的。
张里千先生为首的北大学者们提出中国特色的《实用优选法》:
用不设交互作用项的小正交表,依照序贯设计思想,用多轮正交试验逐步寻到可能最优组合。
也可同样用于控制,以达到设计要求的均值和方差为目的。
目前DOE学界两条发展方向:
(一)寻找最优水平组合,暂不建数模。作为应用数学,只要知道“是什么”,不必知道“为什么”。
(二)建回归方程为目的。
(1)一种思路是研究最小低阶混杂设计,需用经验因素判断,关键仍不能避免混杂。
(2)另一种思路,删减惰性因子,缩减到3、4因子后再用全因子析因设计建数模。
其缺陷是当试验设计水平不够多、不够广时,在原水平时可能是惰性因子,在原水平外可能是非惰性因子,尤其是非线性响应可控因子。
明明是高维空间模型,武断缩减成低维空间模型,缩减了信息后建立的回归方程,对样本拟合也近似了,离拟合总体更远了。
(3)全因子析因设计信息也不齐。
比如2水平2因子全因子析因设计有4次试验,其仅X1xX2考虑交互作用,但忽略了回归因子可能二次方。如全二阶模型需6个参数待估计,应6次试验。
用小样本估计总体的回归系数可信度有多高?
所以英国统计学家肯德尔指出“样本量n应是解释变量个数p的10倍。”(《应用回归分析》p10)
建回归方程的目的是用于预测或控制,对小样本拟合好的回归方程,不一定对总体拟合好!
所以有学者警示:
“一个模型如果对数据拟合得太好可能对预测是槽糕的。”(《试验设计与分析及参数优化》p13)
收起阅读 »
基于非线性数模静态稳健性设计(RPD)的探讨 向 DOE初学者进言(2)
作为用于工业DOE的先驱,在日本应用正交试验近70年,是日本产品高性价比、高可靠性的基础,所以在日本有不懂正交试验只是半个工程师的说法。
国内八十年代开始学习田口正交试验,应用D0E也近40年了。但近期,笔者看到媒体介绍某高科技企业为了寻找刀片切割最佳角度化了4年,意识到当前重提田口方法的静态稳健性设计还是很有必要。
田口方法因不用统计学惯用的統计量和推理方法,常被欧美学者所诟病。有的是击中要害,有的有所误解。比如非全因子析因设计按北大张里千观点属非参数统计系统,不必用参数统计的费歇体系。其对DOE最大贡献,笔者认为是静态稳健性设计,美囯不少DOE权威文献都认可稳健性设计观点。
笔者发现田口静态稳健性设计其数学背景是非线性数模:
即响应曲面应是弯曲的,不弯曲就不能进行稳健性设计。所以不是每一个案例都可应用稳健性设计,如没有方差非线性响应的可控因子,或没有可控因子(或可控因子之间交互作用)抑制噪声因子的显著性交互作用(响应曲面已弯曲),这需要把系统重新设计成非线性数模。有学者认为田口三次设计只有参数和容差设计二次是误解,非线性的系统设计是三次设计中不能缺少的第一步。
近来媒体呼吁,仅快把实验室科研项目转化成量化产品,并质疑为何能造出二弹一星,而不少高品质产品无法国产。二弹一星非量化产品,又无市场竞争的经济性压力,离开经济性谈质量是无意义的。
往往在实验室做出样品性能优异,而批量生产和用户使用时感到质量波动大、可靠性差。量化产品要达到质量可靠性好又经济性好,中间难关不少,原因更复杂。
在休哈特时代之前,用事后检验方法删除超合格限产品保障量化产品质量合格、休哈特时代用统计技术,事前控制生产线质量的波动性、费歇时代认识到作为生产线的上游,设计阶段用DOE分析出可控因子对响应的贡献大小更重要、田口先生认为内外噪声因子对产品质量干扰,是理论设计或实验室成果到量化产品和使用环境中质量波动劣化的原凶。优化水平组合抑制内外噪声的稳健性设计使质量波动稳定,比靠用高价公价差小的零部件传统方法性价比高。
传统用公差小价格贵的零部件减少产品质量波动,是被动的治表方法,而利用合理水平组合抑制内外干扰,是主动廉价的治本的良方。
能抑制噪声干扰达到质量波动小的稳健性设计是保证产品质量稳定之源头。田口先生认为上游设计水平好,已决定了生产线产品质量优良和经济性,所以有好的产品是设计出来的说法。
比如实验室可精选零件参数和理想设计值一致,而量产时,哪怕达到六西格玛水平,零件特性值也必然和理想值有所偏离,最终造成整机质量的波动,即存在产品间噪声干扰。
如可控因子有方差非线性响应特性,仅调整到合适的水平,可降低产品间噪声对响应的干扰,类似用了高价离散性小的零部件的效果。
例如:
设计输入交流220伏,输出直流电压110伏整流变压器。电阻和晶体管放大倍数的变动对输出电压都有影响。晶体管放大倍数A水平时,输出直流电压均值110伏,传统工程技术人士认为已达到设计要求,但其输出电压极差17伏。
当晶体管放大倍数B水平时,输出均值170伏,极差5伏,说明晶体管放大倍数是有方差非线性响应特征的可控因子(离散因子)。稳健性设计选用输出均值170伏设计,仅用输出波动小的水平,达到用公差小高价零部件的效果。电阻是线性响应可控因子(位置因子),其变动不影响输出电压的方差,所以再用电阻把170伏校正到110伏目标值。达到均值等于目标值,而方差又小的目的。如A水平用公差小高价晶体管也能达到这方差小的水平,但经济性差多了。(注意:此案例独立的离散因子和独立的位置因子,两者不可缺一。)
输出响应如正态分布,有均值和方差两个参数,回归方程常见的是响应均值方程,而稳健性设计同时关注响应方差的系统性变异。
欧美文献用重复试验的样本方差表达系统性方差变异性是一种误解,一种组合重复试验的样本方差仅表达试验的随机性变异。
比如上述变压器案例,如用L9的3水平部分正交试验设计,每一水平有3组试验,晶体管放大倍数因子3个水平响应极差大小明显不一。稳健性设计认为响应极差有系统性变异,可能是方差非线性响应因子(离散因子)。
比如有的产品新的很好,使用吋间一长,产生功能衰退,故障多可靠性变差,即时效老化噪声,就是内噪声。传统方法用高价零件增加使用寿命。经典弹簧案例,不同水平组合寿命差十倍,仅調节可控因子水平就可得到长寿设计。
笔者用200元人民帀购买十年电池寿命的电子手表。起初认为其电池容量大,用了5年发现不需要调整时间,始终误差半分钟!容忍了5年中四季温差的外部干扰,5年零件老化和磨损的内部干扰,这里应有稳健性设计技术支撑,不单单是电池的品质好。
实验室中的温度、电压是可控因子,在生产线和用户使用时成为不可控因子,即成为外噪声。如有可控因子与噪声因子有正能量的显著性交互作用,可减弱外噪声的干扰。
比如:
汽车开发初,由于道路平整度的不完美,不平整会使前轮偏离原行进方向,驾驶员需时时刻刻校正方向盘十分累。当前轮呈倒八字倾角的前束设计后,如前轮受不平整影响,小角度偏离后,前轮会自动纠正到原行进方向,驾驶员省力多了。仅改变前轮倾角水平,抑制了路面外噪声的干扰,而不是去减少路面不平整度。
田口方法用信噪比寻优,认为不用信噪比公式就不是田口方法,对于初学者不一定非用田口信噪比寻优不可。
笔者认为DOE可分试验设计的结构表和数据分析两部分,前者是关键,后者用信噪比寻优、建数学模型或其它分析处理试验数据方法仅是不同的学术观点。
信噪比原是电工学一个术语,比如收音机音量设计:差的设计,信号音量放大,噪声也正比例放大。好的设计信号放大要远超噪声放大。田口方法信噪比的意义基于偏离目标值就产生质量经济损失观点:
均值偏离目标值帯来的质量经济损失必须小于方差带来的质量经济损失。
B0X认为田口方法望小、望大型信噪比公式不符合信噪比概念。
其望目型信噪比公式本质是变异系数的倒数,在寻优中必须用位置因子配套,但不是所有案例都能找到不影响方差的位置因子。田口先生用信噪比作为统计量的原意是把均值和方差综合成一个统计量,但望目型有3个参数,笔者认为其望目型公式缺目标值参数,是最大败笔。
寻找最优水平组合最困难的案例是两参数相悖:
均值趋近目标值时,方差变大,或方差趋小时,均值远离目标值。这时需权衡得失,不一定用望目型信噪比公式,可用田口的质量经济损失函数:
即响应分布对目标值的方差=响应分布方差+均值与目标值差的平方。
包括了3个参数。(其二次函数表达质量经济损失函数也是为了计算上方便,虽粗糙,但优于望目型信噪比公式。)
田口稳健性设计革命性的创新是把噪声因子加入正交表,(不是把交互作用项加入正交表)。
比如前变压器案例,正交表中输入电压水平不单是标准220v,以实际使用上下限波动值为上下水平(如支农产品,极差更大),来模拟外噪声。可控因子除标准参数外,实际批量生产零部件上下限为可控因子上下水平,模拟产品间噪声,模拟了批量生产实际使用环境的结果。
学术界常批评田口方法不量化可控因子交互作用。噪声因子是不可控的,难用理论计算出其对响应的影响,通过试验能估计噪声因子对响应的负面贡献和可控因子抑制内外噪声的贡献。如果噪声因子不加入正交表,哪怕正确量化出可控因子之间交互效应,其最优水平组合仅是实验室最优,量产使用时,并不优秀。
学术界另批评田口方法常用3水平正交表,认为2水平加中心点试验可检别响应曲面是否弯曲更简便合理。静态稳健性设计已定性为响应曲面必须是弯曲的,常用3水平正交试验好处是,每一水平的统计意义同等的,可为下一轮寻优的正交试验提供统计意义的信息。而中心点试验和用二水平正交试验不存在同等的统计意义。对望大望小型案例可用2水平,但对望目型3水平是必要的。
对大于4因子案例常常只能用部分正交试验,非全因子析因设计无法精确量化交互效应,所以初学者不必先为不精确的可控因子之间交互效应操心。用加入噪声因子的正交试验,找到最优水平组合就是胜利。待有大数据支撑,可再建模。至于这是可控因子之间交互作用贡献,还是可控因子和噪声因子交互作用的贡献可暂时不去追究,可视为《黑箱》效应。
对于稳健性设计的原理,有学者认为:
“非线性关系降低内部干扰因子影响,干扰因子与控制因子交互作用降低外部干扰或测量干扰因子的影响。”
用可控因子抑制噪声因子案例历史上早有实现,但上升到理论体系是田口先生贡献。
田口方法有不少缺陷,但其基于非参数统计系统的静态稳健性设计思想没过时,是对DOE最大贡献。(非参数统计系统概念另文再述)
收起阅读 »
国内八十年代开始学习田口正交试验,应用D0E也近40年了。但近期,笔者看到媒体介绍某高科技企业为了寻找刀片切割最佳角度化了4年,意识到当前重提田口方法的静态稳健性设计还是很有必要。
田口方法因不用统计学惯用的統计量和推理方法,常被欧美学者所诟病。有的是击中要害,有的有所误解。比如非全因子析因设计按北大张里千观点属非参数统计系统,不必用参数统计的费歇体系。其对DOE最大贡献,笔者认为是静态稳健性设计,美囯不少DOE权威文献都认可稳健性设计观点。
笔者发现田口静态稳健性设计其数学背景是非线性数模:
即响应曲面应是弯曲的,不弯曲就不能进行稳健性设计。所以不是每一个案例都可应用稳健性设计,如没有方差非线性响应的可控因子,或没有可控因子(或可控因子之间交互作用)抑制噪声因子的显著性交互作用(响应曲面已弯曲),这需要把系统重新设计成非线性数模。有学者认为田口三次设计只有参数和容差设计二次是误解,非线性的系统设计是三次设计中不能缺少的第一步。
近来媒体呼吁,仅快把实验室科研项目转化成量化产品,并质疑为何能造出二弹一星,而不少高品质产品无法国产。二弹一星非量化产品,又无市场竞争的经济性压力,离开经济性谈质量是无意义的。
往往在实验室做出样品性能优异,而批量生产和用户使用时感到质量波动大、可靠性差。量化产品要达到质量可靠性好又经济性好,中间难关不少,原因更复杂。
在休哈特时代之前,用事后检验方法删除超合格限产品保障量化产品质量合格、休哈特时代用统计技术,事前控制生产线质量的波动性、费歇时代认识到作为生产线的上游,设计阶段用DOE分析出可控因子对响应的贡献大小更重要、田口先生认为内外噪声因子对产品质量干扰,是理论设计或实验室成果到量化产品和使用环境中质量波动劣化的原凶。优化水平组合抑制内外噪声的稳健性设计使质量波动稳定,比靠用高价公价差小的零部件传统方法性价比高。
传统用公差小价格贵的零部件减少产品质量波动,是被动的治表方法,而利用合理水平组合抑制内外干扰,是主动廉价的治本的良方。
能抑制噪声干扰达到质量波动小的稳健性设计是保证产品质量稳定之源头。田口先生认为上游设计水平好,已决定了生产线产品质量优良和经济性,所以有好的产品是设计出来的说法。
比如实验室可精选零件参数和理想设计值一致,而量产时,哪怕达到六西格玛水平,零件特性值也必然和理想值有所偏离,最终造成整机质量的波动,即存在产品间噪声干扰。
如可控因子有方差非线性响应特性,仅调整到合适的水平,可降低产品间噪声对响应的干扰,类似用了高价离散性小的零部件的效果。
例如:
设计输入交流220伏,输出直流电压110伏整流变压器。电阻和晶体管放大倍数的变动对输出电压都有影响。晶体管放大倍数A水平时,输出直流电压均值110伏,传统工程技术人士认为已达到设计要求,但其输出电压极差17伏。
当晶体管放大倍数B水平时,输出均值170伏,极差5伏,说明晶体管放大倍数是有方差非线性响应特征的可控因子(离散因子)。稳健性设计选用输出均值170伏设计,仅用输出波动小的水平,达到用公差小高价零部件的效果。电阻是线性响应可控因子(位置因子),其变动不影响输出电压的方差,所以再用电阻把170伏校正到110伏目标值。达到均值等于目标值,而方差又小的目的。如A水平用公差小高价晶体管也能达到这方差小的水平,但经济性差多了。(注意:此案例独立的离散因子和独立的位置因子,两者不可缺一。)
输出响应如正态分布,有均值和方差两个参数,回归方程常见的是响应均值方程,而稳健性设计同时关注响应方差的系统性变异。
欧美文献用重复试验的样本方差表达系统性方差变异性是一种误解,一种组合重复试验的样本方差仅表达试验的随机性变异。
比如上述变压器案例,如用L9的3水平部分正交试验设计,每一水平有3组试验,晶体管放大倍数因子3个水平响应极差大小明显不一。稳健性设计认为响应极差有系统性变异,可能是方差非线性响应因子(离散因子)。
比如有的产品新的很好,使用吋间一长,产生功能衰退,故障多可靠性变差,即时效老化噪声,就是内噪声。传统方法用高价零件增加使用寿命。经典弹簧案例,不同水平组合寿命差十倍,仅調节可控因子水平就可得到长寿设计。
笔者用200元人民帀购买十年电池寿命的电子手表。起初认为其电池容量大,用了5年发现不需要调整时间,始终误差半分钟!容忍了5年中四季温差的外部干扰,5年零件老化和磨损的内部干扰,这里应有稳健性设计技术支撑,不单单是电池的品质好。
实验室中的温度、电压是可控因子,在生产线和用户使用时成为不可控因子,即成为外噪声。如有可控因子与噪声因子有正能量的显著性交互作用,可减弱外噪声的干扰。
比如:
汽车开发初,由于道路平整度的不完美,不平整会使前轮偏离原行进方向,驾驶员需时时刻刻校正方向盘十分累。当前轮呈倒八字倾角的前束设计后,如前轮受不平整影响,小角度偏离后,前轮会自动纠正到原行进方向,驾驶员省力多了。仅改变前轮倾角水平,抑制了路面外噪声的干扰,而不是去减少路面不平整度。
田口方法用信噪比寻优,认为不用信噪比公式就不是田口方法,对于初学者不一定非用田口信噪比寻优不可。
笔者认为DOE可分试验设计的结构表和数据分析两部分,前者是关键,后者用信噪比寻优、建数学模型或其它分析处理试验数据方法仅是不同的学术观点。
信噪比原是电工学一个术语,比如收音机音量设计:差的设计,信号音量放大,噪声也正比例放大。好的设计信号放大要远超噪声放大。田口方法信噪比的意义基于偏离目标值就产生质量经济损失观点:
均值偏离目标值帯来的质量经济损失必须小于方差带来的质量经济损失。
B0X认为田口方法望小、望大型信噪比公式不符合信噪比概念。
其望目型信噪比公式本质是变异系数的倒数,在寻优中必须用位置因子配套,但不是所有案例都能找到不影响方差的位置因子。田口先生用信噪比作为统计量的原意是把均值和方差综合成一个统计量,但望目型有3个参数,笔者认为其望目型公式缺目标值参数,是最大败笔。
寻找最优水平组合最困难的案例是两参数相悖:
均值趋近目标值时,方差变大,或方差趋小时,均值远离目标值。这时需权衡得失,不一定用望目型信噪比公式,可用田口的质量经济损失函数:
即响应分布对目标值的方差=响应分布方差+均值与目标值差的平方。
包括了3个参数。(其二次函数表达质量经济损失函数也是为了计算上方便,虽粗糙,但优于望目型信噪比公式。)
田口稳健性设计革命性的创新是把噪声因子加入正交表,(不是把交互作用项加入正交表)。
比如前变压器案例,正交表中输入电压水平不单是标准220v,以实际使用上下限波动值为上下水平(如支农产品,极差更大),来模拟外噪声。可控因子除标准参数外,实际批量生产零部件上下限为可控因子上下水平,模拟产品间噪声,模拟了批量生产实际使用环境的结果。
学术界常批评田口方法不量化可控因子交互作用。噪声因子是不可控的,难用理论计算出其对响应的影响,通过试验能估计噪声因子对响应的负面贡献和可控因子抑制内外噪声的贡献。如果噪声因子不加入正交表,哪怕正确量化出可控因子之间交互效应,其最优水平组合仅是实验室最优,量产使用时,并不优秀。
学术界另批评田口方法常用3水平正交表,认为2水平加中心点试验可检别响应曲面是否弯曲更简便合理。静态稳健性设计已定性为响应曲面必须是弯曲的,常用3水平正交试验好处是,每一水平的统计意义同等的,可为下一轮寻优的正交试验提供统计意义的信息。而中心点试验和用二水平正交试验不存在同等的统计意义。对望大望小型案例可用2水平,但对望目型3水平是必要的。
对大于4因子案例常常只能用部分正交试验,非全因子析因设计无法精确量化交互效应,所以初学者不必先为不精确的可控因子之间交互效应操心。用加入噪声因子的正交试验,找到最优水平组合就是胜利。待有大数据支撑,可再建模。至于这是可控因子之间交互作用贡献,还是可控因子和噪声因子交互作用的贡献可暂时不去追究,可视为《黑箱》效应。
对于稳健性设计的原理,有学者认为:
“非线性关系降低内部干扰因子影响,干扰因子与控制因子交互作用降低外部干扰或测量干扰因子的影响。”
用可控因子抑制噪声因子案例历史上早有实现,但上升到理论体系是田口先生贡献。
田口方法有不少缺陷,但其基于非参数统计系统的静态稳健性设计思想没过时,是对DOE最大贡献。(非参数统计系统概念另文再述)
收起阅读 »
重视图表分析,避过分依赖软件 -向DOE初学者进言(1)
DOE已进入使用软件阶段,因方便常为初学者首选。
DOE只有全因子析因设计才能精确量化交互作用,但大于4因子试验次数太多,使用受碍。
而大大减少试验次数的非全因子析因设计“混杂”不能避免,所以聪明的应用软件也不能百分之百可靠。
比如《实验设计应用指南》(闵亚能)p181例6_10,软件显示结果只有AxD互效应是显著的,而实际应BxC交互效应显著,而AxD交互效应不存在!原因是用了部分析因设计混杂了,经验丰富者“还可以‘猜’一下”,初学者可能成陷阱。
有的学者对多因子案例处理的方法:删除不显著因子或交互作用,缩减至3因子后再析因设计。
这方法也有误区,由于水平取值不够多,在2水平范围中因子可能是不显著性,在2水平之外水平可能是显著性的,(比如响应呈三次函数关系用4水平才能表达其复杂变异性)更有多因子案例,原不显著性因子高阶交互作用呈显著性。比如治爱滋病的鸡尾酒疗法,单个药疗都不显著,多种药混合使用有显著性疗效。
《实验设计与分析6版》蒙哥马利p194案例,其“主”效应图表面看来A+C+D+为最优组合,但从交互作用图显示应A+C-D+最优水平组合,实际证明后者是正确的。
非全因子析因设计中多因子案例中有交互作用的因子,所谓“主”效应实际是正交表的“列”效应,其中混杂了交互效应。所以前述例6_10,如用交互作用图分析即可避免用软件的失误。
正交试验的特点之一,整齐可比性,在交互效应加入后也不一定成立。
所以蒙哥马利认为:“统计方法优点,简单图解法起重要作用。”
“简单方法几乎总是最好的。”比如目测散点图,分辨回归曲线是线性还是非线性应是判断回归数模的第一步。
看来交互作用是DOE最大难点?但是田口方法反而专注于怎样利用正能量的交互作用,这正是稳健性设计全新的思维方法的妙处。(另文再述)
”
收起阅读 »
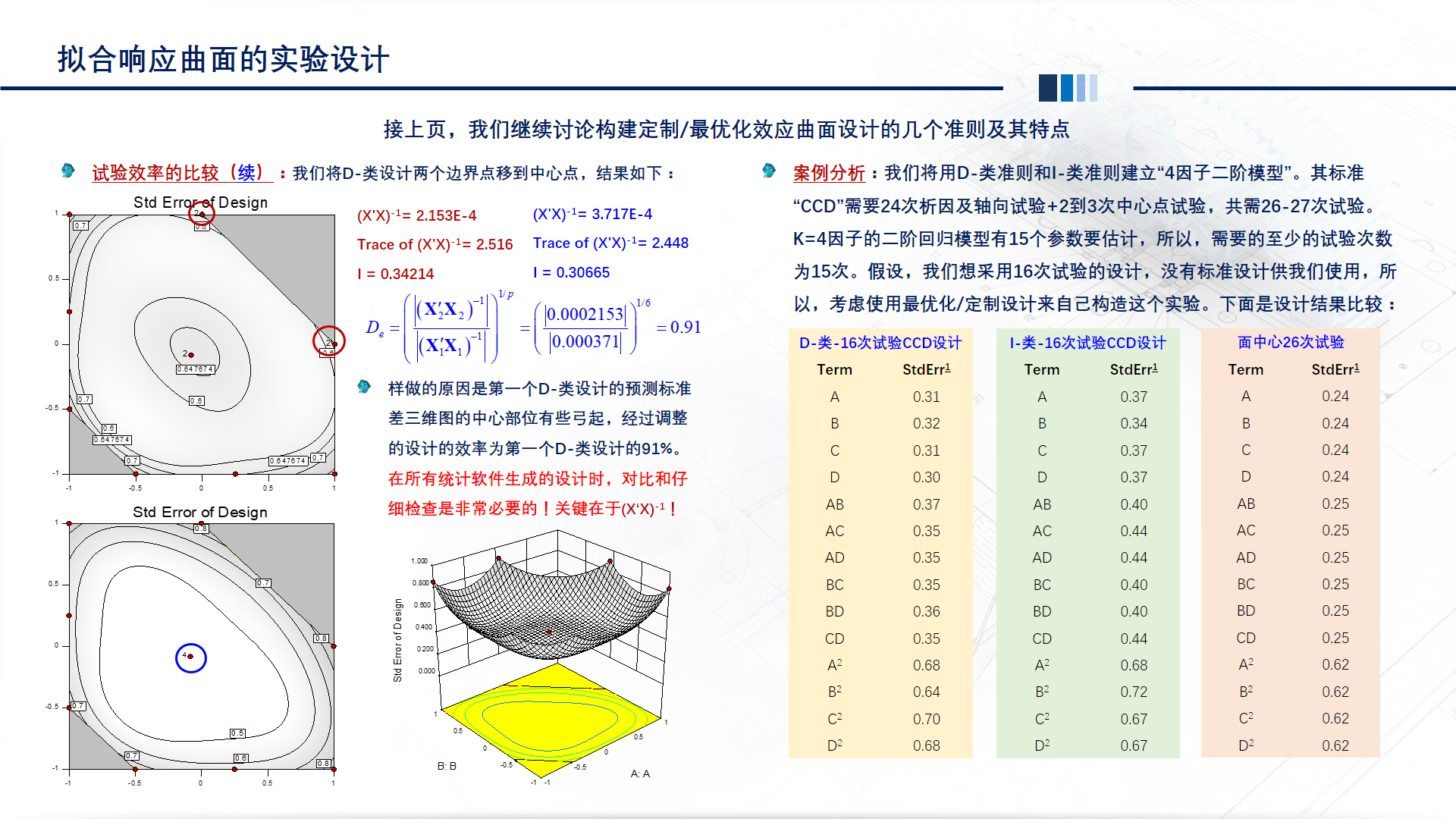
如何在试验开始前比较所采用的的实验设计的效率
DOE实验设计是重要的改善工具,也是统计学应用于解决实际问题的一门学科。虽然历经近百年的发展,至今仍是最为活跃的统计学分支。它的活力主要来自于解决实际问题的有效性。
作为工程技术人员,不仅仅是质量工作者,尤其是研发和工艺工程师,经常要进行“试验”,比如:确定公差、选择产品结构、确定工艺参数、调整加工和制造参数等等。有时候,这样的事情多到我们不认为它们是“试验”,而是日常工作的一部分。
有经验的工程师会有体会:试验是耗力费时的,更麻烦的是,尽管不断调整和优化过程,有的问题还是反复发生。
记得有句话:“不会科学安排试验的工程师,最多只能算半个工程师”。
尤其在精益理念盛行的今天,看得见的浪费容易被消除或减少;但,如果不能科学的安排试验,尽管反复试验,其中的浪费确不太容易引起重视。使用科学的方法来安排试验,应该是精益思想的体现吧。
还有许多年轻有为的质量工作者在不断学习诸如六西格玛,同时也不断解决所谓的质量问题,也需要掌握DOE的基本技术。特别是黑带项目或者从事黑带工作,熟练运用DOE应该是基本功之一。
试验耗力费时,选择实验设计的类型也是很有讲究的:即使同一大类的设计中,不同的设计的“效率”也是不一样的。怎么能采用最少的试验次数获得更多更可靠的信息非常重要。
收起阅读 »
六西格玛培训必掌握的专业术语汇总
ANOVA(ANalysis Of Variance) :变异数分析。一比较两个或以上的群体之间平均值的差异程度, 作为相关性辨别的方法。
Balanced Design :设计在每组试验中有相同的实验单位。
BB(Black Belt) :黑带。
Black Belt Certification :黑带认证。完成两个符合条件的项目后取得的认证。
Block :一群具有同构型的实验单位。
Blocking :一个试验在既定的顺序或条件下完成。任何有妨碍的因子并不会影响真正的结果或重要性。
Capability :能力,达成目标的过程中能维持下去的能力。
Cause & Effect Diagrams :因果关系图。能表达出一个结果及可能的原因两者关系的图表。
Center Points :以所有因子的最高及最低点的中点值来执行的实验。只能用在计量的数据。
CI(Confidence Interval) :信赖区间。响应的数值能真实代表母体,使人信赖的百分比程度。
Confounded Effects :不能被独立预测出的令人困惑的结果。
Confounding :一个或多个结果,无法明确的归因于某个因素或相互间的影响。
Control Chart :控制图。用来辨识一个控制下的操作过程的方法(在既定的统计范畴内)。
Cp(Process Capability) :衡量过程能力的指数 Cp = 公差(Tolerance) / 6s。
Cpk : Performance Capability Index – Cpk = (USL – mean)或(mean - LSL)的最小值除以3s。
CRD (Completely Randomized Design) :完全随机设计。在各种程度下,研究某个重要的因子,而实验以完全随机的顺序来执行,使不可控制的变因最小化。
CTQ Flow down :以非常严谨的方法分配需求,并评估比关键性的产品及其部门的能力。
CTQ(Critical To Quality) :关键品质参数。
Defect :一个用来衡量既定标准的参数,却无法符合其标准。
Defective (Part) :某个被用来衡量既定标准的部分,无法符合该标准的任何条件。单一的缺陷部分可能包含数个缺陷(defects)。
Degrees of Freedom :自由度,分析变异数的一个数值。相当一个独立于用来预测变量的信息个数。
Degrees of Freedom for Error :一个数值,用来分析变异数以预测过程中的干扰度。未对过程的干扰度加以预测,而决定何者是重要的变量及其影响程度,都是无效的。一个大约的衡量准则是,5的误差的自由度为极小值,相当于至少六次的重复。
DOA(Dead on Arrival) :客户接收时无法运作的产品。
DOE(Design of Experiments) :实验设计; 一群母体中的任何一项用来了解高度分配的因子。通常和因子设计有关。
DPMO(Defects Per Million Opportunities) :发现的缺陷个数除以(单位数乘每单位的机率),乘以一百万。
DPPM(Defective Parts Per Million) :外部的阐述, ─缺陷单位个数除以总单位数,乘以一百万。在Cpk的基础下。
DPU(Defects Per Unit) :发现的缺陷个数除以实际衡量的单位数。
Duncan’s Method :邓肯法。一种统计方法,用以决定改变结果的因素其程度。
Effect :当一个因素的水准由低变为高时,对结果产生的平均变化。
Error :误差。过程中的固有变量。当其它变量保持不变时,结果产生的差异。(见noise)。
Estimate :在既定的水准及考量过程中所有因素的影响下,对某结果的预测。(见prediction)。
EVOP(EVolutionay OPeration) :渐进式操作。持续进行所设计的试验而不影响其效率的一种方式。
EWMA(Exponentially Weighted Moving Average) :指数加权移动平均。一个控制曲线法,利用历史数据的指数加权值最小值。
Experimental Region :实验范围。所有可能的因素组合产生可能的实验。亦称做“要素空间”(Factor Space)。
Experimental Unit :实验中被发现及用来衡量的单位。亦称做“分析单位”(unit of analysis)。
F Test :一项统计检定,用来决定两变量间是否有差异存在。
Factor :在实验中能改变的投入要素, 因子。可能以质(例如:附加的种类)或 量(例如:温度、气压)表示。
Factor, Fixed :如果要素的水准明确的被指定,则此要素称做固定的。结论只能以 此要素来推论。结果具重要性。
Factor, Monitored :一项因素(通常是不可控制的,因此不能视为固定的。)在实 验过程中发现,且与部分无法解释的变异相关联。
Factor, Nuisance :妨害的因子。一项已知会在过程中制造差异的因素﹔并无要求 调查这项因子,但亦不可使此因子影响其它重要变因产生的结果。(见blocking)。
Factor, Random :如果要素的水准是随机自母体值中选取时,则此因子称做“随机 的”。变异的组成要素具重要性。
Fixed Effects Factor :有选择地挑选出某水准下的因子。例如,以400度、450度、 500度来做为研究气温的结果。(与做Random Effects Factor比较。)
Fractional 2k Designs :所有的要素都在低水准及高水平下做测试。
Fractional 3k Designs :所有的要素都在三种水准下测试:低、中、高。
Fractional Factorial Experiment :部分因子试验。DOE的集合,只部分探究数个 变量中的两种水准。用来遮蔽住许多琐碎的变量,而集中焦点于主要控制过程的少而重要的变量。
Full Factorial Experiment :全部因子试验。DOE的集体,探究数个变量中的两种 水准,并可取得对主要及相互影响的结果之了解。
Gage R&R(Gage Repeatability and Reproducibility) :某分配的所有变异百分比 的分析,此分配可归因于衡量系统中的变异。
Gage Repeatability :当操纵者利用相同的gage衡量此明显的特性时,可得到相同 的变异。
Gage Reproducibility :当衡量相同部分的特性时,由不同的操作者以相同的gage 衡量其平均变异。
Generator :一个用来创造部分因子设计的相互影响作用。
GLM(General Linear Model) :一个ANOVA的形式,可允许实验设计中些许程 度的不平衡。
HALT─Highly Accelerated Life Testing :为达可靠的设计所用的数种方法中的一种。其概念为测试某产品致其极端(失败)条件,找出失败的根本原因,改善设计,并重复程序。
Histogramv :长条图。表示所搜集资料分布情形的条状图。
Hypothesis :前提,假说。一项利用统计方法来测试的声明。此假设可能被拒绝,或因无够充分的证据而被拒绝。
Interaction :在某情况下,一项因子对某结果影响的水准不同于第二项因子的不同水准。有双向相互影响,三向相互影响等。
IX-MR :Individual X and Moving Range─一个有连续数据点的控制曲线,并有点之间的等级图表。
Kutosis :峰度。是描述某变量所有取值分布形态陡缓程度的统计量。峰度为0表示其数据分布与正态分布的陡缓程度相同;大于0表示比正态分布高峰更加陡峭,为尖顶峰。
Level :某因子的数值或设定。可以是质(如:附加A和附加B)或量(如:1000磅平方英吋,2000平方英吋)。
LSD(Latin Square Design) :一种实验设计,研究其中的一项重要变因,并排除两项干扰因素。
Main Effect :当一项因子由低水准改变至高水准时,其对结果的改变。
MBB(Master Black Belt) :6σ的训练师和顾问师。
Mean :衡量一项变数的中间趋势。原点的第一项要素。
Mean Square :在ANOVA表中的某栏,代表由不同来源的变因导致结果的差异。
Mean Square Error :在ANOVA表中的某项,代表所有因子在给定的水准下,结果所产生的差异。预测由于干扰(误差)对结果产生的差异。
Minitab :目前许多人所选择的统计分析应用软件。
Multiple Comparison Procedure :一种用来决定因子在何种水准下导致结果改变的统计方法。例如:Fisher法、Duncan法、Scheffe法。
Multi-Vari Analysis :一种图解法,将过程中的变化来源拆解为他们基本的组成成分。这种技巧用于初步移除多而琐碎的因子,并准备替代的因子作为设计的实验。
Multivariate Statistical Methods :统计工具,用来分析一组变量以决定他们对数种结果的影响。包括一组多样的统计工具,例如回归、成分法则、因子分析、群组、分别分析。
Nested Design :一项实验设计,其中一种因子因其它变量而设定多种水准。例如:不同厂商提供不同批次。附加物的不同水准等。
Noise :一过程中固有的变因。代表当不改变任何因素时,结果的改变。
Normal Distribution :常态分配,一种钟状的机率曲线,描述许多自然的过程。当情况一再重复且平均发生时。
Normal Probability Plot :一种图标法,用来研究样本是否来自一个常态分配的母体。通常用来检验利用ANOVA的正确性。
One-Way ANOVA :分析单项因素在不同水准下所生的变异。(见ANOVA)。
Optimization :从过程中找出最希望的结果下,其因子和水准的组合。
Pareto Chart :以一般公制单位(次数、元额、时间等)表示事件的条状图。
Plackett-Burman Design :一种设计的实验,用来筛选样本需要的最小量。通常只调查主要的影响,而不预测相互间的影响。
Point Estimate :点估计值。判断某种预言或预定的响应的最好单一值,应该与信心和/ 或预言同时使用。
Pre-control :预先控制。当流程开始时,建立统计上合理可能性的优势的一种方法。
Prediction Interval :预言距离。反应值的信赖百分比范围就是未来观察值会落在的范围内。
Prediction:预言。用于所有已知因素的一套标准的最佳评估响应。
Process Demographics :人口统计数据流。产生响应的时候期间各种因素条件/ 状态的清单。这些帮助我们理解过程的范围也许可排除问题。
Random Effects Factor : 随机影响因素。随意地从可定义母体选择层次的一个因素。 举例来说,从五批生产量中任意选择一批调查其影响 (固定影响因素的比较)。
Randomization :随机选择。实验这行中将次序混合完全实用。
Randomized Block Design : 集区随机实验。调查兴趣的因素及一个令人讨厌的事物因素其相对阻塞的实验 。
Repetition :再现性。在一个处理结合上执行几个实验单元。 与复制形成对比。
Replication :重复性。反复的执行一些相同的实验情况;提供了制程中噪音的评估。
Residuals :残余。在既定的因素情况下,观察的反应和预定的反应之间的差异 。用于模型证实和过程 的调查。
Resolution :解答。部分因子设计的描述,提供因素间相互影响的程度。
Response :反应。实验期间量测过的制程输出。
RSM(Response Surface Methodology) :反应曲面法。实验设计中一门检查和理解这些极少的曲率。子集包括中央合成设计在星星或者面上的点。
R-Square :判定系数。在反应中变异百分比由控制的因素来解释。
Run :一套过程条件由规定实验方面所有因素的层次定义。同样, 叫作处理结合。
Run chart :经营图表。提供一些统计分析能力和机率资料的连续时间序列图。
Scatter Plot :散布图表。显示两个变异数间关系的图表(dot plot)。
SCN(Supplier Change Notice) : 供货商变革通知。要求改变一个购买部分的讯息装置,由供货商对企业开始, 或是企业对供货商开始。
Screening Experiment :筛选实验。用来描述一过程的技术 (通常为因素标准的变化呈现反应中的线性变化) (与 RSM作比较).
Sigma :标准差。使用具有一套变异数数据的统计计算。其值为变异数的平方根。
Signal to Noise Ratio :讯号噪声比。当因素标准中没有变化时,由于改变与可变性相关的因素标准取决于反应中的可变性的一个比例 。
Skewness :偏度。描述某变量取值分布对称性的统计量,能够影响使用ANOVA的有效性。偏度为0表示其数据分布形态与正态分布偏度相同;大于0表示为正偏或右偏,即有一条长尾巴拖在右边。
SPC(Statistical Process Control) :统计流程管理。对希望的状态在修正以后,使用安定性最好的监控流程。
Trivial Many :锁碎多数。长期被认为在流程上会有影响的因素,但实际上说明了成果上很少的差异。
T-Test :正常的母体下,样本平均数的统计比较 。
Two-Way ANOVA :双因子变异数分析。为以若干标准调查两个原素的变异数分析。
Two-way Interaction Plot:双因子互动图。一个因素的平均数反应的散布图 (纵轴)就像一个因素(横轴)和第二个因素的每一个标准的平均反应由线所连接出来。
Type I Error :没事却误判为有事的错误。 其组合机率称为 a。
Type II Error :确实不同,却误判为相同。其组合机率称为 b。
UCL or LCL :管制的上、下限 – 管制图表的统计范围。
Unbalanced Design :不平衡设计。每一个处理结合中实验单元不相等的数字的设计或执行。
USL or LSL :规格的上、下限– 设计标准的界限。
Variance:变异。提供一个量测散布的方法。其平方根为标准差,The 2nd moment around the mean。
Vital Few :关键多数。是管理流程中的关键因素。
ZB(Z benchmark) :认为流程是短期变异数的中心(在目标方面)。
来源:文章转载自张驰咨询 收起阅读 »
Balanced Design :设计在每组试验中有相同的实验单位。
BB(Black Belt) :黑带。
Black Belt Certification :黑带认证。完成两个符合条件的项目后取得的认证。
Block :一群具有同构型的实验单位。
Blocking :一个试验在既定的顺序或条件下完成。任何有妨碍的因子并不会影响真正的结果或重要性。
Capability :能力,达成目标的过程中能维持下去的能力。
Cause & Effect Diagrams :因果关系图。能表达出一个结果及可能的原因两者关系的图表。
Center Points :以所有因子的最高及最低点的中点值来执行的实验。只能用在计量的数据。
CI(Confidence Interval) :信赖区间。响应的数值能真实代表母体,使人信赖的百分比程度。
Confounded Effects :不能被独立预测出的令人困惑的结果。
Confounding :一个或多个结果,无法明确的归因于某个因素或相互间的影响。
Control Chart :控制图。用来辨识一个控制下的操作过程的方法(在既定的统计范畴内)。
Cp(Process Capability) :衡量过程能力的指数 Cp = 公差(Tolerance) / 6s。
Cpk : Performance Capability Index – Cpk = (USL – mean)或(mean - LSL)的最小值除以3s。
CRD (Completely Randomized Design) :完全随机设计。在各种程度下,研究某个重要的因子,而实验以完全随机的顺序来执行,使不可控制的变因最小化。
CTQ Flow down :以非常严谨的方法分配需求,并评估比关键性的产品及其部门的能力。
CTQ(Critical To Quality) :关键品质参数。
Defect :一个用来衡量既定标准的参数,却无法符合其标准。
Defective (Part) :某个被用来衡量既定标准的部分,无法符合该标准的任何条件。单一的缺陷部分可能包含数个缺陷(defects)。
Degrees of Freedom :自由度,分析变异数的一个数值。相当一个独立于用来预测变量的信息个数。
Degrees of Freedom for Error :一个数值,用来分析变异数以预测过程中的干扰度。未对过程的干扰度加以预测,而决定何者是重要的变量及其影响程度,都是无效的。一个大约的衡量准则是,5的误差的自由度为极小值,相当于至少六次的重复。
DOA(Dead on Arrival) :客户接收时无法运作的产品。
DOE(Design of Experiments) :实验设计; 一群母体中的任何一项用来了解高度分配的因子。通常和因子设计有关。
DPMO(Defects Per Million Opportunities) :发现的缺陷个数除以(单位数乘每单位的机率),乘以一百万。
DPPM(Defective Parts Per Million) :外部的阐述, ─缺陷单位个数除以总单位数,乘以一百万。在Cpk的基础下。
DPU(Defects Per Unit) :发现的缺陷个数除以实际衡量的单位数。
Duncan’s Method :邓肯法。一种统计方法,用以决定改变结果的因素其程度。
Effect :当一个因素的水准由低变为高时,对结果产生的平均变化。
Error :误差。过程中的固有变量。当其它变量保持不变时,结果产生的差异。(见noise)。
Estimate :在既定的水准及考量过程中所有因素的影响下,对某结果的预测。(见prediction)。
EVOP(EVolutionay OPeration) :渐进式操作。持续进行所设计的试验而不影响其效率的一种方式。
EWMA(Exponentially Weighted Moving Average) :指数加权移动平均。一个控制曲线法,利用历史数据的指数加权值最小值。
Experimental Region :实验范围。所有可能的因素组合产生可能的实验。亦称做“要素空间”(Factor Space)。
Experimental Unit :实验中被发现及用来衡量的单位。亦称做“分析单位”(unit of analysis)。
F Test :一项统计检定,用来决定两变量间是否有差异存在。
Factor :在实验中能改变的投入要素, 因子。可能以质(例如:附加的种类)或 量(例如:温度、气压)表示。
Factor, Fixed :如果要素的水准明确的被指定,则此要素称做固定的。结论只能以 此要素来推论。结果具重要性。
Factor, Monitored :一项因素(通常是不可控制的,因此不能视为固定的。)在实 验过程中发现,且与部分无法解释的变异相关联。
Factor, Nuisance :妨害的因子。一项已知会在过程中制造差异的因素﹔并无要求 调查这项因子,但亦不可使此因子影响其它重要变因产生的结果。(见blocking)。
Factor, Random :如果要素的水准是随机自母体值中选取时,则此因子称做“随机 的”。变异的组成要素具重要性。
Fixed Effects Factor :有选择地挑选出某水准下的因子。例如,以400度、450度、 500度来做为研究气温的结果。(与做Random Effects Factor比较。)
Fractional 2k Designs :所有的要素都在低水准及高水平下做测试。
Fractional 3k Designs :所有的要素都在三种水准下测试:低、中、高。
Fractional Factorial Experiment :部分因子试验。DOE的集合,只部分探究数个 变量中的两种水准。用来遮蔽住许多琐碎的变量,而集中焦点于主要控制过程的少而重要的变量。
Full Factorial Experiment :全部因子试验。DOE的集体,探究数个变量中的两种 水准,并可取得对主要及相互影响的结果之了解。
Gage R&R(Gage Repeatability and Reproducibility) :某分配的所有变异百分比 的分析,此分配可归因于衡量系统中的变异。
Gage Repeatability :当操纵者利用相同的gage衡量此明显的特性时,可得到相同 的变异。
Gage Reproducibility :当衡量相同部分的特性时,由不同的操作者以相同的gage 衡量其平均变异。
Generator :一个用来创造部分因子设计的相互影响作用。
GLM(General Linear Model) :一个ANOVA的形式,可允许实验设计中些许程 度的不平衡。
HALT─Highly Accelerated Life Testing :为达可靠的设计所用的数种方法中的一种。其概念为测试某产品致其极端(失败)条件,找出失败的根本原因,改善设计,并重复程序。
Histogramv :长条图。表示所搜集资料分布情形的条状图。
Hypothesis :前提,假说。一项利用统计方法来测试的声明。此假设可能被拒绝,或因无够充分的证据而被拒绝。
Interaction :在某情况下,一项因子对某结果影响的水准不同于第二项因子的不同水准。有双向相互影响,三向相互影响等。
IX-MR :Individual X and Moving Range─一个有连续数据点的控制曲线,并有点之间的等级图表。
Kutosis :峰度。是描述某变量所有取值分布形态陡缓程度的统计量。峰度为0表示其数据分布与正态分布的陡缓程度相同;大于0表示比正态分布高峰更加陡峭,为尖顶峰。
Level :某因子的数值或设定。可以是质(如:附加A和附加B)或量(如:1000磅平方英吋,2000平方英吋)。
LSD(Latin Square Design) :一种实验设计,研究其中的一项重要变因,并排除两项干扰因素。
Main Effect :当一项因子由低水准改变至高水准时,其对结果的改变。
MBB(Master Black Belt) :6σ的训练师和顾问师。
Mean :衡量一项变数的中间趋势。原点的第一项要素。
Mean Square :在ANOVA表中的某栏,代表由不同来源的变因导致结果的差异。
Mean Square Error :在ANOVA表中的某项,代表所有因子在给定的水准下,结果所产生的差异。预测由于干扰(误差)对结果产生的差异。
Minitab :目前许多人所选择的统计分析应用软件。
Multiple Comparison Procedure :一种用来决定因子在何种水准下导致结果改变的统计方法。例如:Fisher法、Duncan法、Scheffe法。
Multi-Vari Analysis :一种图解法,将过程中的变化来源拆解为他们基本的组成成分。这种技巧用于初步移除多而琐碎的因子,并准备替代的因子作为设计的实验。
Multivariate Statistical Methods :统计工具,用来分析一组变量以决定他们对数种结果的影响。包括一组多样的统计工具,例如回归、成分法则、因子分析、群组、分别分析。
Nested Design :一项实验设计,其中一种因子因其它变量而设定多种水准。例如:不同厂商提供不同批次。附加物的不同水准等。
Noise :一过程中固有的变因。代表当不改变任何因素时,结果的改变。
Normal Distribution :常态分配,一种钟状的机率曲线,描述许多自然的过程。当情况一再重复且平均发生时。
Normal Probability Plot :一种图标法,用来研究样本是否来自一个常态分配的母体。通常用来检验利用ANOVA的正确性。
One-Way ANOVA :分析单项因素在不同水准下所生的变异。(见ANOVA)。
Optimization :从过程中找出最希望的结果下,其因子和水准的组合。
Pareto Chart :以一般公制单位(次数、元额、时间等)表示事件的条状图。
Plackett-Burman Design :一种设计的实验,用来筛选样本需要的最小量。通常只调查主要的影响,而不预测相互间的影响。
Point Estimate :点估计值。判断某种预言或预定的响应的最好单一值,应该与信心和/ 或预言同时使用。
Pre-control :预先控制。当流程开始时,建立统计上合理可能性的优势的一种方法。
Prediction Interval :预言距离。反应值的信赖百分比范围就是未来观察值会落在的范围内。
Prediction:预言。用于所有已知因素的一套标准的最佳评估响应。
Process Demographics :人口统计数据流。产生响应的时候期间各种因素条件/ 状态的清单。这些帮助我们理解过程的范围也许可排除问题。
Random Effects Factor : 随机影响因素。随意地从可定义母体选择层次的一个因素。 举例来说,从五批生产量中任意选择一批调查其影响 (固定影响因素的比较)。
Randomization :随机选择。实验这行中将次序混合完全实用。
Randomized Block Design : 集区随机实验。调查兴趣的因素及一个令人讨厌的事物因素其相对阻塞的实验 。
Repetition :再现性。在一个处理结合上执行几个实验单元。 与复制形成对比。
Replication :重复性。反复的执行一些相同的实验情况;提供了制程中噪音的评估。
Residuals :残余。在既定的因素情况下,观察的反应和预定的反应之间的差异 。用于模型证实和过程 的调查。
Resolution :解答。部分因子设计的描述,提供因素间相互影响的程度。
Response :反应。实验期间量测过的制程输出。
RSM(Response Surface Methodology) :反应曲面法。实验设计中一门检查和理解这些极少的曲率。子集包括中央合成设计在星星或者面上的点。
R-Square :判定系数。在反应中变异百分比由控制的因素来解释。
Run :一套过程条件由规定实验方面所有因素的层次定义。同样, 叫作处理结合。
Run chart :经营图表。提供一些统计分析能力和机率资料的连续时间序列图。
Scatter Plot :散布图表。显示两个变异数间关系的图表(dot plot)。
SCN(Supplier Change Notice) : 供货商变革通知。要求改变一个购买部分的讯息装置,由供货商对企业开始, 或是企业对供货商开始。
Screening Experiment :筛选实验。用来描述一过程的技术 (通常为因素标准的变化呈现反应中的线性变化) (与 RSM作比较).
Sigma :标准差。使用具有一套变异数数据的统计计算。其值为变异数的平方根。
Signal to Noise Ratio :讯号噪声比。当因素标准中没有变化时,由于改变与可变性相关的因素标准取决于反应中的可变性的一个比例 。
Skewness :偏度。描述某变量取值分布对称性的统计量,能够影响使用ANOVA的有效性。偏度为0表示其数据分布形态与正态分布偏度相同;大于0表示为正偏或右偏,即有一条长尾巴拖在右边。
SPC(Statistical Process Control) :统计流程管理。对希望的状态在修正以后,使用安定性最好的监控流程。
Trivial Many :锁碎多数。长期被认为在流程上会有影响的因素,但实际上说明了成果上很少的差异。
T-Test :正常的母体下,样本平均数的统计比较 。
Two-Way ANOVA :双因子变异数分析。为以若干标准调查两个原素的变异数分析。
Two-way Interaction Plot:双因子互动图。一个因素的平均数反应的散布图 (纵轴)就像一个因素(横轴)和第二个因素的每一个标准的平均反应由线所连接出来。
Type I Error :没事却误判为有事的错误。 其组合机率称为 a。
Type II Error :确实不同,却误判为相同。其组合机率称为 b。
UCL or LCL :管制的上、下限 – 管制图表的统计范围。
Unbalanced Design :不平衡设计。每一个处理结合中实验单元不相等的数字的设计或执行。
USL or LSL :规格的上、下限– 设计标准的界限。
Variance:变异。提供一个量测散布的方法。其平方根为标准差,The 2nd moment around the mean。
Vital Few :关键多数。是管理流程中的关键因素。
ZB(Z benchmark) :认为流程是短期变异数的中心(在目标方面)。
来源:文章转载自张驰咨询 收起阅读 »
DOE试验设计所涉及的命令
DOE试验设计所涉及的命令:
通过试验设计方法可以对过程进行改善。可以通过试验设计筛选出对过程变异存在重要影响的因素,MINITAB可以分析这些因素及其交互作用对过程的影向状况, 可以通过分析发现这些因素的最优水平设置从而优化过程性能。MINITAB的试验设计分析渉及以下命令:
1. Factorial
(1) Create Factorial Design: 生成二水平全因子、分部因子和 “Plackett-Burman”设计表。
(2) Define Custom Factorial Design: 从已经输入到工作表中的数提创建一个因子试验设计方案。
(3) Analyze Factorial Design:分析二水平全因子和分部因子设计以及“Plackett-Burman”设计。
(4) Factorial Plots: 显示二水平全因子、分部因子和 “Plackett-Burman”试验设计的主要影响图、交互作用影响图和三维图。
(5)Contour Surface/Wireframe Plots: 画出轮廓图和三维图响应表面图。
(6) Response Optimizer: 计算优化的解决方案并画出交互影响图以确定一组同时优化所有响应变量的因子水平。
(7) Overlaid Contour Plot:为多个响应变量画出轮廓图。
2. Response Sarface
(1)Create Response Surface Design: 生成 “Box-Be-hnken”和中心复合试验设计表。
(2) Define Custom Response Surface Design:从已经输入到工作表中的数据创建一个响应表面设计方案。
(3) Select optimal Design: 选择一个设计点的子集, 增加一个设计或评估一个设计。
(4) Analyze Response Surface Design: 分析响应表面设计。
(5)RS Plots: 画出一个轮廓图或三维响应表面图。
(6) Response Optimizer:计算优化的解決方案并画出交互影响图以确定一组同时优化所有响应变量的因子水平。
(7) Overlaid Contour Plot: 为多个响应变量画出轮廓图,
3.Mixture
(1)Create Mixture Design: 生成混合水平试验设计表
(2) Define Custom Mixture Design: 从已经输入到工作表中的数据创建一个混合水平设计方案
(3) Select optimal Design: 选择一个设计点的子集, 增加一个设计或评估一个设计
(4) Analyze Mixture Design: 分析混合水平试验设计
(5)Overlaid Contour Plot: 为多个响应变量画出轮廊图
4. Taguchi
(1) Create Taguchi Design: 生成田口正交试验设计表
(2) Define Custom Taguchi Design: 从已经输入到工作表中的数据创建一个田口试验设计方案
(3) Analyze Taguchi Design: 分析田口试验设计
(4) Predict Taguchi Results: 预测田口试验设计结果
5.DOE
(1)Modify Design:改变因子名和水平
(2)Display Design:改变试验顺序并为工作表中的因子编码。
收起阅读 »
通过试验设计方法可以对过程进行改善。可以通过试验设计筛选出对过程变异存在重要影响的因素,MINITAB可以分析这些因素及其交互作用对过程的影向状况, 可以通过分析发现这些因素的最优水平设置从而优化过程性能。MINITAB的试验设计分析渉及以下命令:
1. Factorial
(1) Create Factorial Design: 生成二水平全因子、分部因子和 “Plackett-Burman”设计表。
(2) Define Custom Factorial Design: 从已经输入到工作表中的数提创建一个因子试验设计方案。
(3) Analyze Factorial Design:分析二水平全因子和分部因子设计以及“Plackett-Burman”设计。
(4) Factorial Plots: 显示二水平全因子、分部因子和 “Plackett-Burman”试验设计的主要影响图、交互作用影响图和三维图。
(5)Contour Surface/Wireframe Plots: 画出轮廓图和三维图响应表面图。
(6) Response Optimizer: 计算优化的解决方案并画出交互影响图以确定一组同时优化所有响应变量的因子水平。
(7) Overlaid Contour Plot:为多个响应变量画出轮廓图。
2. Response Sarface
(1)Create Response Surface Design: 生成 “Box-Be-hnken”和中心复合试验设计表。
(2) Define Custom Response Surface Design:从已经输入到工作表中的数据创建一个响应表面设计方案。
(3) Select optimal Design: 选择一个设计点的子集, 增加一个设计或评估一个设计。
(4) Analyze Response Surface Design: 分析响应表面设计。
(5)RS Plots: 画出一个轮廓图或三维响应表面图。
(6) Response Optimizer:计算优化的解決方案并画出交互影响图以确定一组同时优化所有响应变量的因子水平。
(7) Overlaid Contour Plot: 为多个响应变量画出轮廓图,
3.Mixture
(1)Create Mixture Design: 生成混合水平试验设计表
(2) Define Custom Mixture Design: 从已经输入到工作表中的数据创建一个混合水平设计方案
(3) Select optimal Design: 选择一个设计点的子集, 增加一个设计或评估一个设计
(4) Analyze Mixture Design: 分析混合水平试验设计
(5)Overlaid Contour Plot: 为多个响应变量画出轮廊图
4. Taguchi
(1) Create Taguchi Design: 生成田口正交试验设计表
(2) Define Custom Taguchi Design: 从已经输入到工作表中的数据创建一个田口试验设计方案
(3) Analyze Taguchi Design: 分析田口试验设计
(4) Predict Taguchi Results: 预测田口试验设计结果
5.DOE
(1)Modify Design:改变因子名和水平
(2)Display Design:改变试验顺序并为工作表中的因子编码。
收起阅读 »
分享六西格玛培训中控制阶段的的主要任务、流程步骤
一、六西格玛控制阶段的的主要任务是:
1、制定和向流程拥有者移交流程改善的控制计划,使其有能力和方法持续控制和检查流程改善,具体包括:
•确认未完结的项目内容、责任人和完成时间;
•明确改善后的具体流程控制方法、责任人和异常出现时的措施;
•1年内定期确认改善效果并提供监督/报告流程的改善保持状况。
2、项目团队成员继续收集所关注关键参数Y, Xs的数据,运用SPC等工具监控项目所做改善的保持状况。
3、通过各种手段、工具确认控制计划并完成实时控制,保证改善的项目结果一直得到保持。
4、运用控制图和防错设计来监测和控制流程变异:
.控制图的预警机制可用于保持流程改善的稳定性,在SPC控制图给出异常信号时,就要采取措施来修正流程参数。
.在条件许可的情况下,应尽量采用防错设计保证流程不会产生变异。
5、发现、找出该项目中可供学习借鉴的地方,推广到企业内部其他类似的问题上,使改善效果不断扩大。
6、将跟踪完毕后的项目报告纳入企业的六西格玛管理数据库,供企业其他的项目团队参考。
二、控制阶段的流程步骤
控制的主要工作流程是跟踪评价改进效果并进行验证,同时制定且必须文档化控制措施。
在项目的实施过程中,将改进措施落实到流程中,在此过程中,首先要收集Y的数据,确认改善后的效果,然后还应评价改善后的流程能力;将改进措施纳入设计图纸、工艺文件或技术规范中,使其文档化、标准化和制度化;将改进结果应用到类似项目中。这一阶段的工作包括:
1、重新进行测量系统分析
特别对关键输入因素X应用测量系统分析技术,确定它的测量系统的波动情况是否满足产品系统的测试需求,或再相应调整X的取值范围,另外还需进行y的测量系统分析,因为改进后,流程的波动变小,流程趋于稳定,原有的测量系统已不能区分流程波动,所以需要重新进行Y的测量系统分析。
2、重新评价所关注流程的流程能力
必要时建立控制图,对流程特性应用SPC技术进行实时控制,识别流程性能中出现的特殊原因波动,实施减小波动的措施,重新计算流程能力并保持改进成果。
3、制定和严格执行流程控制计划
将流程改善或流程改进的更改进行文档化,制定严格的流程控制计划,并纳入企业质量管理体系中。
每一个六西格玛管理项目的成果首先要制度化、文档化,以确保项目成果得到不断延续、没有弱化。然后需要定期监控、测量,确保改进效果,这样需要持续一年。为了保证六西格玛管理的可信度和权威,所以,企业需要建立有关改善类项目实施情况的评价与检查制度,定期评审改进项目的进展情况,提出下一阶段的工作重点和方向。
文章摘自:张驰咨询
收起阅读 »
1、制定和向流程拥有者移交流程改善的控制计划,使其有能力和方法持续控制和检查流程改善,具体包括:
•确认未完结的项目内容、责任人和完成时间;
•明确改善后的具体流程控制方法、责任人和异常出现时的措施;
•1年内定期确认改善效果并提供监督/报告流程的改善保持状况。
2、项目团队成员继续收集所关注关键参数Y, Xs的数据,运用SPC等工具监控项目所做改善的保持状况。
3、通过各种手段、工具确认控制计划并完成实时控制,保证改善的项目结果一直得到保持。
4、运用控制图和防错设计来监测和控制流程变异:
.控制图的预警机制可用于保持流程改善的稳定性,在SPC控制图给出异常信号时,就要采取措施来修正流程参数。
.在条件许可的情况下,应尽量采用防错设计保证流程不会产生变异。
5、发现、找出该项目中可供学习借鉴的地方,推广到企业内部其他类似的问题上,使改善效果不断扩大。
6、将跟踪完毕后的项目报告纳入企业的六西格玛管理数据库,供企业其他的项目团队参考。
二、控制阶段的流程步骤
控制的主要工作流程是跟踪评价改进效果并进行验证,同时制定且必须文档化控制措施。
在项目的实施过程中,将改进措施落实到流程中,在此过程中,首先要收集Y的数据,确认改善后的效果,然后还应评价改善后的流程能力;将改进措施纳入设计图纸、工艺文件或技术规范中,使其文档化、标准化和制度化;将改进结果应用到类似项目中。这一阶段的工作包括:
1、重新进行测量系统分析
特别对关键输入因素X应用测量系统分析技术,确定它的测量系统的波动情况是否满足产品系统的测试需求,或再相应调整X的取值范围,另外还需进行y的测量系统分析,因为改进后,流程的波动变小,流程趋于稳定,原有的测量系统已不能区分流程波动,所以需要重新进行Y的测量系统分析。
2、重新评价所关注流程的流程能力
必要时建立控制图,对流程特性应用SPC技术进行实时控制,识别流程性能中出现的特殊原因波动,实施减小波动的措施,重新计算流程能力并保持改进成果。
3、制定和严格执行流程控制计划
将流程改善或流程改进的更改进行文档化,制定严格的流程控制计划,并纳入企业质量管理体系中。
每一个六西格玛管理项目的成果首先要制度化、文档化,以确保项目成果得到不断延续、没有弱化。然后需要定期监控、测量,确保改进效果,这样需要持续一年。为了保证六西格玛管理的可信度和权威,所以,企业需要建立有关改善类项目实施情况的评价与检查制度,定期评审改进项目的进展情况,提出下一阶段的工作重点和方向。
文章摘自:张驰咨询
收起阅读 »