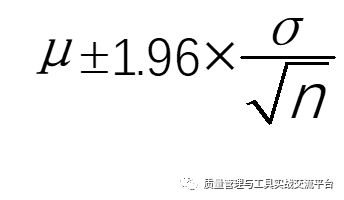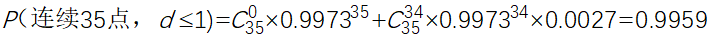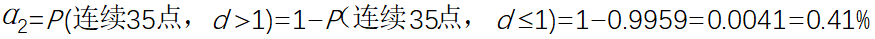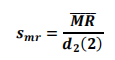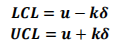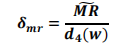正态分布简说
各位大佬,本文仅指交流学习,如有雷同,纯属巧合。望多多指教!
本文简要概述正态分布一些相关知识,浓缩了一些书本上的知识,也增加了一些个人实际工作经验心得。
正态分布(Normal distribution)又名高斯分布(Gaussian distribution),简单来说,它描述的就是正常分布,比如产品尺寸、人体体重、财富等分布,多数人都会集中在某个区间。尽管在高斯之前,有些数学家已经发现了这一规律,但高斯是第一个将其完善的人。
它是一个“高性价比”的思考工具,因为它简单易学且应用广。正态分布广泛存在于自然界、社会科学、人文科学等领域,比如动物骨骼大小、考试成绩、产品质量指标、农作物产量等数据分布大多符合这一规律。在统计推断中,它是最重要的一类概率分布,也是许多统计方法的理论基础。
01 正态分布的背景知识
平均值、方差、标准差三个部分如同土壤,会很大程度影响正态分布这棵树的生长情况。因此,在介绍正态分布前,我需要简单介绍它们(如你已掌握,可直接跳至 02正态分布的主干知识 进行阅读~)。
由于样本量的不同,平均值、方差、标准差可以分“总体”和“样本”两类。为强化对比,在后文的介绍中,我会在它们前面加上限定词,即“总体”或“样本”。如果没有限定词,那么平均值、方差、标准差所指代的就是总体的平均值、方差、标准差。
平均值
平均值(平均数)是我们的小学旧识。温故知新,因为它会在新情景下返场,因此我打算简单提一下。用简洁、严谨、优美的数学语言,一句话回顾平均值:“平均值是一组数据中所有数据之和再除以这组数据的个数,用于表示一组数据的集中趋势。”
在正态分布中,由于样本量不同,平均值又可以分为总体平均值(μ)和样本平均值(x拔)两类,两者的计算方法是一样的,只是符号有差异。小贴士:希腊字母“μ”,发音为mu,是代表总体平均值的符号;“x一横”这个符号念作“X bar”,用于代表样本平均值。
方差
方差是衡量一组数据波动大小的统计量。我们学习方差最重要的,不在于掌握繁杂的计算,而是能够根据其结果,了解所有数据的状态。
方差分为两类:总体方差和样本方差。两者的基本思路一致,但最大的差别在于样本量不同,前者是整体,后者是整体中的部分。
若x1,x2,x3......xn的平均数为μ,则总体方差可表示为:
小贴士:希腊字母“ ∑” 的小写形式为“σ”,英译音为Sigma,大小写符号都念“西格玛”。
1和10两个数字,总体平均值μ=5.5的简单例子,来看公式如何使用。
回到总体方差和样本方差区别的话题,这里举个简单的例子来说明。假设我们想知道中国人身高的标准差,但因人、财、物力有限,我们不可能把所有人都量一遍,因此,只能退而求其次,采取抽样策略,用样本标准差来推测整体,这时,我们就会用到样本方差。
样本方差和总体方差计算上略有区别,主要体现在分母上。不同于总体方差的分母为n,样本方差的分母为n-1。这里“-1”是为了修正样本方差对总体方差的估计偏差,这种现象被称为“贝塞尔校正”(Bessel's correction)。
这个减去的“1”,不特指任何一个数,它代表那个失去“独立客观”的维度(自由度)。
样本方差的计算公式如下:
因此,在计算样本标准差(S,即样本方差开根号)时,其分母也是n−1而不是n(即样本大小减1)。这里在后文标准差的部分还会提到。
小贴士:样本标准差的分母为什么为n-1在数学领域已被证明,是较复杂的内容,这里不做过多展开,有兴趣的读者可查阅相关资料哦~
在公式的应用过程中,你或许会觉得计算很麻烦(事实也确实如此)。好消息是,计算在方差中并不是最重要的,我们要做的,是关注总体方差(σ²)的值,并由此了解方差想告诉我们的秘密:数据内部的状态如何。
在投资分析中,尤其是在股票投资中,方差是一个有用的统计工具,它可以帮助投资者了解投资组合的风险水平。同样的回报率,方差越小,则风险越低。
标准差
标准差(Standard Deviation)是方差的算术平均数的平方根,也用于反映一个数据集的离散程度。标准差实际上就是方差开根。整体标准差用σ表示,样本标准差用s表示。两者的公式如图:
我们来做个三者在“总体”和“样本”符号系统区别上的总结。详见下表:
当我们谈论一个正态分布时,通常是在谈论一个总体的分布,而不是一个样本的分布。因此,使用 μ 来表示正态分布的均值是合适的。
均值、方差、标准差的背景介绍已结束。别走开,下节更精彩,主角闪亮登场~
02 正态分布的主干知识
正态分布
正态分布一种常见的连续概率分布,它在自然科学和社会科学中常用于表示未知的随机变量。若随机变量X服从一个数学期望为μ、方差为σ²的正态分布,则记为N(μ,σ²)。
正态分布的曲线呈钟型,因此人们又经常称之为“钟形曲线”。正态分布虽有无数种形态,但仍由μ(平均值)和σ(标准差)两个数值决定。其中,μ决定了正态分布的位置,σ决定了分布的幅度。理解了这一点,你就不需要单独记忆每一个正态分布图啦。
现在,让我们一起来看一些有代表性的正态分布图吧(下面的文字浓度有点高,值得多看几遍~):
当μ=0,σ=1时,这个正态分布就是标准正态分布,(见下图红线)。
以正态分布为参考标准,μ为负则图形向左移动(见下图绿线),反之,μ为正,则图形向右移动。
μ不变,σ越小,则正态分布曲线越陡峭(见下图蓝线),图像越“高瘦”,反之则越平缓(见下图黄线),图像越“胖”。
数学语言中的“服从”是指“符合”、“遵从”的意思,一般指事物符合数学中的发展规律。
另外,数学术语中,“期望”或“数学期望”是一个重要的概念,特别是在概率论和统计学中。它表示随机变量的预期值或平均值。除了上面的例子,正态分布其实还有数种形态,但它们的模型主要由μ(平均值)和σ(标准差)两个数值决定。
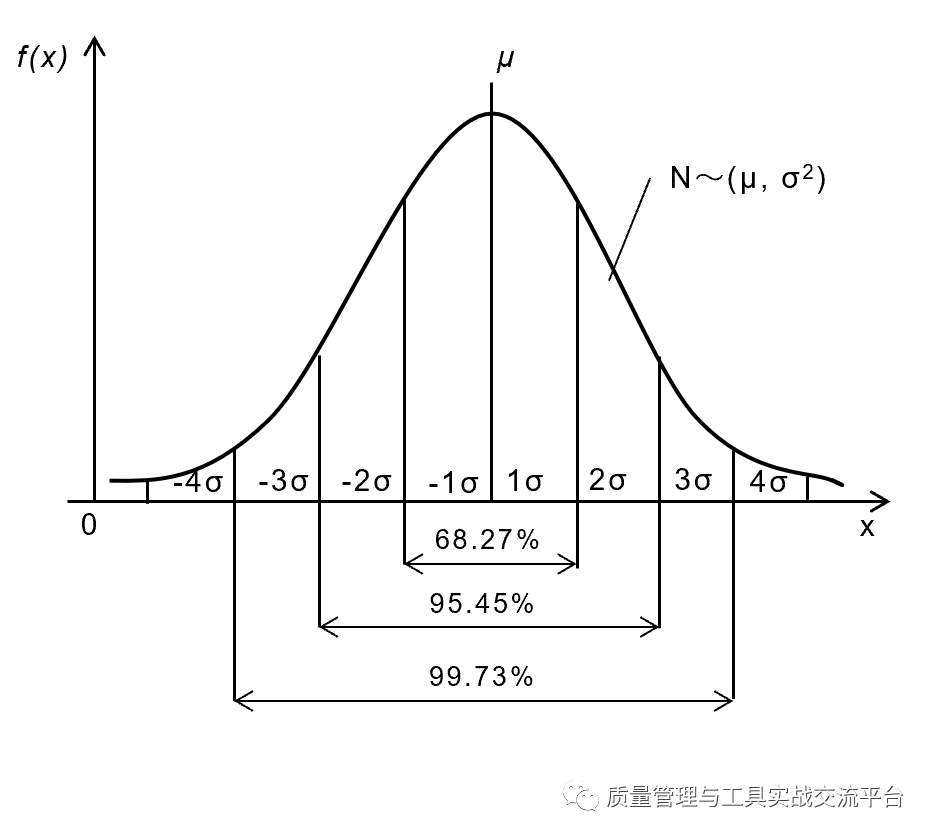
介绍了决定正态分布曲线的关键参数后,我们再来看看关于曲线下方覆盖面积呈现的规律。在距离平均值±1的标准差(即±σ)范围内,集中着约全体68.26%的数据;距离平均值±2的标准差(即±2σ),集中着约95.45%的数据;距离平均值±3的标准差(即±3σ),包含着99.73%的数据。曲线下方覆盖的面积,在统计学上被称“置信区间”。
(1)有大约68%的可能性,动态范围不超过平均值±σ。在一个班上,一班的平均分为80分,如果标准差为5分,我们就有68%的置信度说,考虑到随机性的影响,这个班的平均成绩应落在75~85之间,而不是之外。
(2)有大约95%的可能性,动态范围不超过平均值±2σ,即两个σ的置信度是95%。做科学试验时,通常需要有95%的置信度,才能得到大家认可的结论;在产品质检中,可以通过抽样检测来估计产品的平均质量水平,并利用95%置信区间来评估这个估计的可靠性。
(3)如果我们进一步扩大误差范围到±3σ,那么这个置信度就提高到99.7%。在要求极高的实验中,我们甚至会要求达到99.7%的置信度,甚至更高.
小贴士:总体正态分布图vs样本正态分布图(符号区别)
03 正态分布的标准化
在02正态分布的主干知识中,我们介绍了影响正态分布形态的土壤(平均值、方差、标准差),以及由此长出的小树(正态分布的图像)。结束前,我想跟大家介绍一个与正态分布有关的常用小工具。
标准化与查表求概率
虽然通过观察图也能把握大致情况,但计算数值后会更便于理解,也方便向他人展示。好消息是,Z转换(标准化)可以实现统一尺度。
对于数据集中的每一个数值X,可使用以下公式进行标准化:
在这个公式中,Z是转换后的标准值,X 是原始数据点的值,μ是原始数据的平均值和σ是原始数据的标准差。
别被公式吓到,放进日常的简单应用场景就豁然开朗了。
小A参加了小学模拟考试,数学得了73分,英语得了76分。数学平均分是60分,英语平均分是68分。那么,小A的数学成绩和英文成绩,哪一个相对来说比较好呢?(得分均按照正态分布)实际上,仅这些条件是无法进行判断的,还需要能够表示全体离散程度的标准差。现在,我们假定数学是标准差为8分的正态分布,英语则是标准差为6分的正态分布。
用Z变换的公式可得:
数学 : (得分-平均分)÷标准差=(73-60)÷8=1.625
英语 : (得分-平均分)÷标准差=(76-68)÷6=1.333
也就是说,当标准差为1时,小A的数学、英语成绩标准差分别是1.625、1.333。不同学科的成绩转化为标准得分后,变得可比较了。
另外,用“标准得分=1”进行了标准化,“平均值”会变成什么样呢?本来,平均分根据科目的不同而不同,但以标准得分进行分布的时候,平均值为0。
因此,在对成绩进行“标准化”时,分布会变为平均值=0、标准差=1的标准正态分布。需注意的是,标准化改变的只是图的位置,比如向左或向右平移,但并不会改变“高矮胖瘦”。
完成z变换,我们就通过可以利用z值表找到对应的概率值啦。这里会用到“标准正态分布表”。
这个表是前人整理好的数据,用起来也很方便。首先,我们要看最左手列,去查阅Z至小数点后1位数,之后,我们再查最上一行,看Z的第二位小数,左右交叉得到的数,就是我们需要找的数。
放到小A的例子中,数学的标准差为1.625、英语的标准差为1.333。我们来试试查这个表。以数学为例,先看最左列,Z至小数点后1位数为1.6,接着,再看最上行,Z的第2位小数我取0.02,交叉得到的数就是0.9474(蓝色方框中的数)。英语的查阅方式同理,取值为0.9082。
查表后,就是分析数据了。数学取值为0.9474,英语为0.9082,即数学约处于94.74%的水平,英语处于90.82%的水平。如果参加全国数学、英语模拟考试的人有1万人,小A数学大概处于526名的位置((1-0.9474)x10000=526名),英语处于972名的位置。用图表示更清晰,这里以数学为例:
收起阅读 »
本文简要概述正态分布一些相关知识,浓缩了一些书本上的知识,也增加了一些个人实际工作经验心得。
正态分布(Normal distribution)又名高斯分布(Gaussian distribution),简单来说,它描述的就是正常分布,比如产品尺寸、人体体重、财富等分布,多数人都会集中在某个区间。尽管在高斯之前,有些数学家已经发现了这一规律,但高斯是第一个将其完善的人。
它是一个“高性价比”的思考工具,因为它简单易学且应用广。正态分布广泛存在于自然界、社会科学、人文科学等领域,比如动物骨骼大小、考试成绩、产品质量指标、农作物产量等数据分布大多符合这一规律。在统计推断中,它是最重要的一类概率分布,也是许多统计方法的理论基础。
01 正态分布的背景知识
平均值、方差、标准差三个部分如同土壤,会很大程度影响正态分布这棵树的生长情况。因此,在介绍正态分布前,我需要简单介绍它们(如你已掌握,可直接跳至 02正态分布的主干知识 进行阅读~)。
由于样本量的不同,平均值、方差、标准差可以分“总体”和“样本”两类。为强化对比,在后文的介绍中,我会在它们前面加上限定词,即“总体”或“样本”。如果没有限定词,那么平均值、方差、标准差所指代的就是总体的平均值、方差、标准差。
平均值
平均值(平均数)是我们的小学旧识。温故知新,因为它会在新情景下返场,因此我打算简单提一下。用简洁、严谨、优美的数学语言,一句话回顾平均值:“平均值是一组数据中所有数据之和再除以这组数据的个数,用于表示一组数据的集中趋势。”
在正态分布中,由于样本量不同,平均值又可以分为总体平均值(μ)和样本平均值(x拔)两类,两者的计算方法是一样的,只是符号有差异。小贴士:希腊字母“μ”,发音为mu,是代表总体平均值的符号;“x一横”这个符号念作“X bar”,用于代表样本平均值。
方差
方差是衡量一组数据波动大小的统计量。我们学习方差最重要的,不在于掌握繁杂的计算,而是能够根据其结果,了解所有数据的状态。
方差分为两类:总体方差和样本方差。两者的基本思路一致,但最大的差别在于样本量不同,前者是整体,后者是整体中的部分。
若x1,x2,x3......xn的平均数为μ,则总体方差可表示为:
小贴士:希腊字母“ ∑” 的小写形式为“σ”,英译音为Sigma,大小写符号都念“西格玛”。
1和10两个数字,总体平均值μ=5.5的简单例子,来看公式如何使用。
回到总体方差和样本方差区别的话题,这里举个简单的例子来说明。假设我们想知道中国人身高的标准差,但因人、财、物力有限,我们不可能把所有人都量一遍,因此,只能退而求其次,采取抽样策略,用样本标准差来推测整体,这时,我们就会用到样本方差。
样本方差和总体方差计算上略有区别,主要体现在分母上。不同于总体方差的分母为n,样本方差的分母为n-1。这里“-1”是为了修正样本方差对总体方差的估计偏差,这种现象被称为“贝塞尔校正”(Bessel's correction)。
这个减去的“1”,不特指任何一个数,它代表那个失去“独立客观”的维度(自由度)。
样本方差的计算公式如下:
因此,在计算样本标准差(S,即样本方差开根号)时,其分母也是n−1而不是n(即样本大小减1)。这里在后文标准差的部分还会提到。
小贴士:样本标准差的分母为什么为n-1在数学领域已被证明,是较复杂的内容,这里不做过多展开,有兴趣的读者可查阅相关资料哦~
在公式的应用过程中,你或许会觉得计算很麻烦(事实也确实如此)。好消息是,计算在方差中并不是最重要的,我们要做的,是关注总体方差(σ²)的值,并由此了解方差想告诉我们的秘密:数据内部的状态如何。
在投资分析中,尤其是在股票投资中,方差是一个有用的统计工具,它可以帮助投资者了解投资组合的风险水平。同样的回报率,方差越小,则风险越低。
标准差
标准差(Standard Deviation)是方差的算术平均数的平方根,也用于反映一个数据集的离散程度。标准差实际上就是方差开根。整体标准差用σ表示,样本标准差用s表示。两者的公式如图:
我们来做个三者在“总体”和“样本”符号系统区别上的总结。详见下表:
当我们谈论一个正态分布时,通常是在谈论一个总体的分布,而不是一个样本的分布。因此,使用 μ 来表示正态分布的均值是合适的。
均值、方差、标准差的背景介绍已结束。别走开,下节更精彩,主角闪亮登场~
02 正态分布的主干知识
正态分布
正态分布一种常见的连续概率分布,它在自然科学和社会科学中常用于表示未知的随机变量。若随机变量X服从一个数学期望为μ、方差为σ²的正态分布,则记为N(μ,σ²)。
正态分布的曲线呈钟型,因此人们又经常称之为“钟形曲线”。正态分布虽有无数种形态,但仍由μ(平均值)和σ(标准差)两个数值决定。其中,μ决定了正态分布的位置,σ决定了分布的幅度。理解了这一点,你就不需要单独记忆每一个正态分布图啦。
现在,让我们一起来看一些有代表性的正态分布图吧(下面的文字浓度有点高,值得多看几遍~):
当μ=0,σ=1时,这个正态分布就是标准正态分布,(见下图红线)。
以正态分布为参考标准,μ为负则图形向左移动(见下图绿线),反之,μ为正,则图形向右移动。
μ不变,σ越小,则正态分布曲线越陡峭(见下图蓝线),图像越“高瘦”,反之则越平缓(见下图黄线),图像越“胖”。
数学语言中的“服从”是指“符合”、“遵从”的意思,一般指事物符合数学中的发展规律。
另外,数学术语中,“期望”或“数学期望”是一个重要的概念,特别是在概率论和统计学中。它表示随机变量的预期值或平均值。除了上面的例子,正态分布其实还有数种形态,但它们的模型主要由μ(平均值)和σ(标准差)两个数值决定。
介绍了决定正态分布曲线的关键参数后,我们再来看看关于曲线下方覆盖面积呈现的规律。在距离平均值±1的标准差(即±σ)范围内,集中着约全体68.26%的数据;距离平均值±2的标准差(即±2σ),集中着约95.45%的数据;距离平均值±3的标准差(即±3σ),包含着99.73%的数据。曲线下方覆盖的面积,在统计学上被称“置信区间”。
(1)有大约68%的可能性,动态范围不超过平均值±σ。在一个班上,一班的平均分为80分,如果标准差为5分,我们就有68%的置信度说,考虑到随机性的影响,这个班的平均成绩应落在75~85之间,而不是之外。
(2)有大约95%的可能性,动态范围不超过平均值±2σ,即两个σ的置信度是95%。做科学试验时,通常需要有95%的置信度,才能得到大家认可的结论;在产品质检中,可以通过抽样检测来估计产品的平均质量水平,并利用95%置信区间来评估这个估计的可靠性。
(3)如果我们进一步扩大误差范围到±3σ,那么这个置信度就提高到99.7%。在要求极高的实验中,我们甚至会要求达到99.7%的置信度,甚至更高.
小贴士:总体正态分布图vs样本正态分布图(符号区别)
03 正态分布的标准化
在02正态分布的主干知识中,我们介绍了影响正态分布形态的土壤(平均值、方差、标准差),以及由此长出的小树(正态分布的图像)。结束前,我想跟大家介绍一个与正态分布有关的常用小工具。
标准化与查表求概率
虽然通过观察图也能把握大致情况,但计算数值后会更便于理解,也方便向他人展示。好消息是,Z转换(标准化)可以实现统一尺度。
对于数据集中的每一个数值X,可使用以下公式进行标准化:
在这个公式中,Z是转换后的标准值,X 是原始数据点的值,μ是原始数据的平均值和σ是原始数据的标准差。
别被公式吓到,放进日常的简单应用场景就豁然开朗了。
小A参加了小学模拟考试,数学得了73分,英语得了76分。数学平均分是60分,英语平均分是68分。那么,小A的数学成绩和英文成绩,哪一个相对来说比较好呢?(得分均按照正态分布)实际上,仅这些条件是无法进行判断的,还需要能够表示全体离散程度的标准差。现在,我们假定数学是标准差为8分的正态分布,英语则是标准差为6分的正态分布。
用Z变换的公式可得:
数学 : (得分-平均分)÷标准差=(73-60)÷8=1.625
英语 : (得分-平均分)÷标准差=(76-68)÷6=1.333
也就是说,当标准差为1时,小A的数学、英语成绩标准差分别是1.625、1.333。不同学科的成绩转化为标准得分后,变得可比较了。
另外,用“标准得分=1”进行了标准化,“平均值”会变成什么样呢?本来,平均分根据科目的不同而不同,但以标准得分进行分布的时候,平均值为0。
因此,在对成绩进行“标准化”时,分布会变为平均值=0、标准差=1的标准正态分布。需注意的是,标准化改变的只是图的位置,比如向左或向右平移,但并不会改变“高矮胖瘦”。
完成z变换,我们就通过可以利用z值表找到对应的概率值啦。这里会用到“标准正态分布表”。
这个表是前人整理好的数据,用起来也很方便。首先,我们要看最左手列,去查阅Z至小数点后1位数,之后,我们再查最上一行,看Z的第二位小数,左右交叉得到的数,就是我们需要找的数。
放到小A的例子中,数学的标准差为1.625、英语的标准差为1.333。我们来试试查这个表。以数学为例,先看最左列,Z至小数点后1位数为1.6,接着,再看最上行,Z的第2位小数我取0.02,交叉得到的数就是0.9474(蓝色方框中的数)。英语的查阅方式同理,取值为0.9082。
查表后,就是分析数据了。数学取值为0.9474,英语为0.9082,即数学约处于94.74%的水平,英语处于90.82%的水平。如果参加全国数学、英语模拟考试的人有1万人,小A数学大概处于526名的位置((1-0.9474)x10000=526名),英语处于972名的位置。用图表示更清晰,这里以数学为例:
收起阅读 »
小谈SPC管控
A公司:对应的文件和定义都是清晰的,对应的系统配置和人员配置是完善的,对应的培训也是跟上的。实际执行是生产线按照Control Plan提供样本,由QA技术员收集数据,触发SPC规则后,QA技术员按照文件定义通知设备技术员停机或者调机重新送样或者触发OCAP。由PE定期去检查Control Limit和配置对应的SPC chart,并进行月度分析Cpk的表现(1.33,1.33-1.67,1.67)。至于Control Limit的设置,要求只能收严或者平移,Control Limit由PE掌控,当然是肯定没法严格按照SPC去计算Control Limit,可以认为是Levey-Jennings的方法去计算的。客户来审核时,选择一些Chart表现好的即可,一般不秀OOC的chart给客户看,毕竟看到时需要解释。对于SPC监控的项目,比客户要求的特殊特性,要多很多,客户一般要求行业通用的,而工艺管控就需要监控更多的项目。
B公司:对应的文件和定义都是清晰的,对应的系统配置和人员配置是完善的,对应的培训也是跟上的。测量站点是定义到流程站点的,必须过测量站点才能到下一站,实际执行是专门的Metrology团队负责按照文件定义抽取样品进行测量并上传数据到系统,系统根据配置的SPEC和Control Limit进行判断,触发规则后触发OCAP,质量技术员和工艺技术员按照要求处理系统的OCAP,OCAP没处理完时lot是无法移动到下一站的,所以生产和质量是需要配合及时让lot移动。对于Control Limit,部分chart的Control Limit变更是需要客户同意的。并且配备有团队查看是否有Chart的Control Limit太松,或者说触发OOC的频率很高,如果有,就需要对应的人员去提交变更且通过评审后进行更新Control Limit,还需要对应的PE去解释OOC多次出现的原因。SPC管控从一开始投工程lot就开始设置control limit,并根据各阶段然后更新对应的control limit。
总结:SPC可以对特殊特性和工程参数(例如电导率、药水浓度、压力、线体速度、水流大小、温度、液位等)进行管控。重点是,根据实际情况和人员配置和系统配置,进行有效的SPC管控。管控的项目和频率,当然可以根据表现和阶段,进行删减和增减频率。来料SPC监控也是存在的。其实良率也可以建立类似SPC的管理,例如Defect Ratio管控,良率Baseline管控, Defect Ratio Baseline管控。管控的项目一般会比客户要求的多很多。每个lot的数据,也可以进行by-lot Cpk管控。
补充,以上包括总结的内容,全都是企业在执行的,而不是理论派。 收起阅读 »
B公司:对应的文件和定义都是清晰的,对应的系统配置和人员配置是完善的,对应的培训也是跟上的。测量站点是定义到流程站点的,必须过测量站点才能到下一站,实际执行是专门的Metrology团队负责按照文件定义抽取样品进行测量并上传数据到系统,系统根据配置的SPEC和Control Limit进行判断,触发规则后触发OCAP,质量技术员和工艺技术员按照要求处理系统的OCAP,OCAP没处理完时lot是无法移动到下一站的,所以生产和质量是需要配合及时让lot移动。对于Control Limit,部分chart的Control Limit变更是需要客户同意的。并且配备有团队查看是否有Chart的Control Limit太松,或者说触发OOC的频率很高,如果有,就需要对应的人员去提交变更且通过评审后进行更新Control Limit,还需要对应的PE去解释OOC多次出现的原因。SPC管控从一开始投工程lot就开始设置control limit,并根据各阶段然后更新对应的control limit。
总结:SPC可以对特殊特性和工程参数(例如电导率、药水浓度、压力、线体速度、水流大小、温度、液位等)进行管控。重点是,根据实际情况和人员配置和系统配置,进行有效的SPC管控。管控的项目和频率,当然可以根据表现和阶段,进行删减和增减频率。来料SPC监控也是存在的。其实良率也可以建立类似SPC的管理,例如Defect Ratio管控,良率Baseline管控, Defect Ratio Baseline管控。管控的项目一般会比客户要求的多很多。每个lot的数据,也可以进行by-lot Cpk管控。
补充,以上包括总结的内容,全都是企业在执行的,而不是理论派。 收起阅读 »
细节决定成败
"细节决定成败"是一句俗语,也是一种哲理,指的是讲究细节能决定事件的走向。
有一首民谣是这样的:
少了一个钉子,坏了一只蹄铁;
坏了一只蹄铁,折了一匹战马;
折了一匹战马,伤了一位国王;
伤了一位国王,输了一场战争;
输了一场战争,亡了一个帝国。
说的是1485年,英国国王理查三世要面临一场重要的战争,这场战争关系到国家的生死存亡。
在战斗开始之前,国王让马夫去备好自己最喜爱的战马。马夫立即找到铁匠,吩咐他快点给马掌钉上马蹄铁。铁匠先钉了三个马掌,在钉第四个时发现还缺了一个钉子,马掌当然不牢固。
马夫将这个情况报告给国王,眼看战斗即将开始,国王根本就来不得及在意这第四个马蹄铁,就匆匆赶回战场了。战场上,国王骑着马领着他的士兵冲锋陷阵。突然间,一只马蹄铁脱落了,战马仰身跌翻在地,国王也被重重地摔在了地上。一见国王倒下,士兵们就自顾自地逃命去了,整支军队在一瞬间土崩瓦解。敌军趁机反击,并在战斗中俘虏了国王。
国王此时才意识到那颗钉子的重要性,就这样,理查三世的国家就败在了一颗小小的马蹄钉上。
这是一个典型的细节决定成败的小故事,简单易懂。
我们做软件系统也是如此,很多系统的功能模块基本相同,流程看上去也大同小异,似乎用哪一家都可以满足业务需求。
但实际使用起来体验相去甚远,优秀的系统正是赢在细节:流程设计是否考虑全面,权限设计是否合规合理,用户界面是否操作便捷…
也欢迎大家联系我们,免费试用软件。
收起阅读 »
有一首民谣是这样的:
少了一个钉子,坏了一只蹄铁;
坏了一只蹄铁,折了一匹战马;
折了一匹战马,伤了一位国王;
伤了一位国王,输了一场战争;
输了一场战争,亡了一个帝国。
说的是1485年,英国国王理查三世要面临一场重要的战争,这场战争关系到国家的生死存亡。
在战斗开始之前,国王让马夫去备好自己最喜爱的战马。马夫立即找到铁匠,吩咐他快点给马掌钉上马蹄铁。铁匠先钉了三个马掌,在钉第四个时发现还缺了一个钉子,马掌当然不牢固。
马夫将这个情况报告给国王,眼看战斗即将开始,国王根本就来不得及在意这第四个马蹄铁,就匆匆赶回战场了。战场上,国王骑着马领着他的士兵冲锋陷阵。突然间,一只马蹄铁脱落了,战马仰身跌翻在地,国王也被重重地摔在了地上。一见国王倒下,士兵们就自顾自地逃命去了,整支军队在一瞬间土崩瓦解。敌军趁机反击,并在战斗中俘虏了国王。
国王此时才意识到那颗钉子的重要性,就这样,理查三世的国家就败在了一颗小小的马蹄钉上。
这是一个典型的细节决定成败的小故事,简单易懂。
我们做软件系统也是如此,很多系统的功能模块基本相同,流程看上去也大同小异,似乎用哪一家都可以满足业务需求。
但实际使用起来体验相去甚远,优秀的系统正是赢在细节:流程设计是否考虑全面,权限设计是否合规合理,用户界面是否操作便捷…
也欢迎大家联系我们,免费试用软件。
收起阅读 »
控制图教程和示例
无论您是刚开始使用控制图,还是精通统计过程控制,都会在我们的控制图相关的文章中找到一些有价值的信息和引人深思的内容。
不同类型的控制图
您在统计学中最先学到的内容之一是,当涉及到数据时,没有一种方法能够放之四海皆准。为了从分析中获得最有用和最可靠的信息,需要选择最适合您的数据类型的方法类型。
对于控制图也是如此。尽管有一些控制图的使用频率极高,但是可供使用的控制图有许多,选择正确的控制图能够对可行性信息和误报(或漏报)进行区分。
《我应当使用哪个控制图?》 简要概述了最常见的控制图,并探讨了如何使用“协助”来帮助您选择适合您的情况的控制图。如果您是控制图新手,并且想了解有关我们为何使用控制图的更多背景,请查看《控制图显示重要的变异》。
我们在《超越“普通”控制图:EWMA 控制图》中赞颂了一个不太常用的控制图。
在 《Minitab 软件开发中使用 Laney P' 控制图》中,Dawn Keller 探讨了 P' 控制图及其变体之间的区别,Tammy Serensits 在《P 和 U 控制图和林堡干酪:一种糟糕的组合》中对此进行了描述。
一定要记住事情并不总是看起来那么复杂,有时候简单的解决方案和更复杂的方法一样有效。查看《放轻松:创建运行图》了解原委。
控制图教程
我们的许多 Minitab 博主都谈到了在特定条件下选择、创建和解释控制图的过程。如果您的数据无法在子组中收集,您可能需要了解《如何创建和读取 I-MR 控制图》。
如果您的数据可以在子组中收集,则在谈到《控制图:子组大小很重要》时,您将需要了解具体原因。
通常,有用的做法是以基于日历的增量查看控制图数据,在《创建控制图以比较月度变化》和创建控制图以比较月度变化(第 2 部分)》系列博客中探讨了每月方法。
如果您想了解您的过程改进所带来的差异,请查看《改进前后的过程分析:具有阶段的历史控制图》和《设置阶段:在控制图中说明过程变更》。
尽管控制图的基本理念非常简单,但解释真实世界的控制图可能有点棘手。请务必阅读 《 Minitab 中的控制图稳定性报告包括示例模式》帖子,了解“协助”中的一个重要功能。
最后,我们的一位专家级统计培训师为您建议了《五种使控制图更有效的方法》。
控制图示例
控制图最常用于质量改进和保证,但它们几乎适用于任何涉及变异的情况。
在将业务质量改进应用到个人生活的示例中,我最喜欢 Bill Howell 的示例,他将自己的六西格玛专业知识应用于糖尿病的(成功)管理。了解他如何使用《控制图控制血糖》。
我们的一些博主将控制图应用于他们的个人兴趣爱好,包括《控制图:合理子组和 Marshmallow Peeps!》中的假日糖果和《P 控制图问题:不受控的 Cycle LaneYs!》中的自行车骑行。
如果您对运动感兴趣,不妨看看控制图如何揭示《应在何时拦下 NHL 守门员》。或者为照看宇宙而考虑《信噪比:检测外星人和异常因素》。最后,像我这样欲罢不能的读者可能也有兴趣看看控制图与文学的相关性,正如 Cody Steele 在《 Laney P' 控制图展示 Poe 如何在《厄舍古屋的倒塌中创造强度》中所阐述的那样。 最后,想问大家是如何使用控制图的?
查看文章中提及的文章,请评论留言或私信客服。 收起阅读 »
如何使结晶颗粒大小均等?
Tate & Lyle 是食品与饮料行业的全球领导者,他们的口号是“生产优质食品”,在以下领域有着令人惊叹的辉煌成就:将玉米、木薯淀粉和其他原料制作成配料,以改进食品的口感、质地和营养。该公司在美国最知名的产品之一是甜味剂 SPLENDA® 三氯蔗糖。
当 Tate & Lyle 面临玉米葡萄糖精制过程的挑战时,该公司选择 Minitab 软件来解决问题。
挑战:使结晶颗粒大小均等
在 Adam Russell 最初担任 Tate & Lyle 全球运营黑带大师时,他面临着以下挑战:使他们生产的玉米葡萄糖的颗粒保持同等大小。
“结晶过程的质量特征的一项关键因素就是颗粒大小分布”,Russell 表示,“这究竟为何如此重要?20-30 年前,我们产品的目标客户所期待的是玉米葡萄糖的口感和质地能接近普通的食用糖或蔗糖。为此,我们必须确保颗粒大小分布在一定范围内”。
Tate & Lyle 所面临的难题是,一些颗粒的大小在可接受范围之外,而他们无法找到原因。该公司罗列了一些他们认为对颗粒大小变异造成影响的传统因素:
温度
压力
流速
pH
传导性
相关因素还在不断增加。
Minitab 如何帮助他们
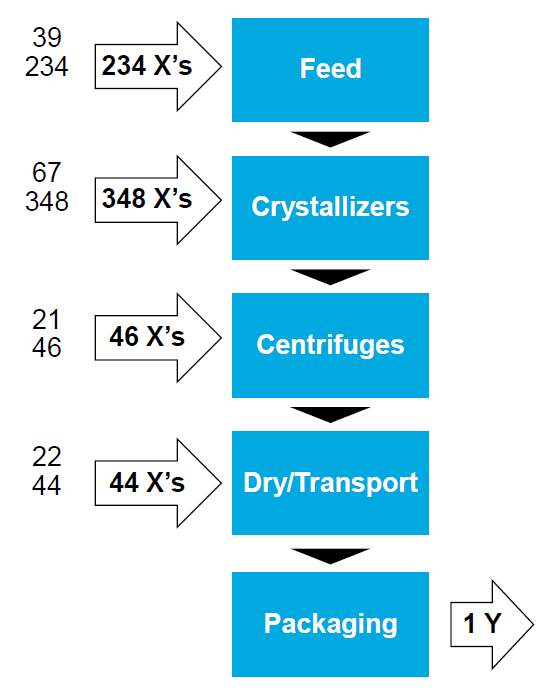
Tate & Lyle 在 Companion by Minitab(现为 Minitab Engage®)中创建的过程图简化版本。在玉米葡萄糖结晶过程中,糖浆由精炼厂提供,然后进行结晶(需要数天完成),接着用离心机进行分离,脱水并装袋,销售给客户。
为解决问题,该公司第一步使用 Companion by Minitab (现为 Minitab Engage®)创建了过程图,详细体现了结晶过程(详细了解过程图)。颗粒大小分布不能可靠地控制在严格范围之内,因此他们想要了解造成变异的原因以及如何进行控制。
“所有项都在一家化工厂内进行测量”,Russell 说道,“每个可能的点都拥有发送器,可为数据历史功能提供信息。这本身非常棒,但也为我们带来了难题,信息量太大,我根本无从着手”。
为了直观地了解颗粒大小数据,Russell 和他的团队使用 Minitab Statistical Software 创建了如下 Xbar chart 控制图.
虽然这些变量之间的多种关系都是非线性的,但是这也证实要发现它们相互之间的影响是非常困难的。此外,颗粒大小在它装袋销售给客户之前是未知的,因为在这之前它处于干燥阶段,其形态是介于液体和固体之间的凝胶状,称为“浆体”。
此类模型具有 1,000 多个可能的输入。多个单独的回归模型并不能寻找到答案。
关键过程指标是制成品的变异系数 (CV),在此显示在使用 Minitab Statistical Software 创建的 Xbar 控制图中。
由于多个预测变量以极其复杂的方式相互影响,因此需要采用有组织的方法来标识哪些预测变量对颗粒大小分布的影响最大。他们需要使用 TreeNet 中的 Salford Predictive Modeler (SPM).
“只使用传统建模技术的话,非常困难”,Russell 表示,“我们很难了解变量与结果之间的关系。幸运的是,SPM 的 TreeNet 使我们可以轻松地专注于关键预测变量,并使我们能够设计出能够有效处理这些预测变量的策略。我坚信 Minitab 和 SPM 的 TreeNet 算法可以有效地进行协作。当然,SPM 不能替代 Minitab 或其他统计程序,但当我们将两者结合使用时,我认为我们能更快获得答案,这再好不过了”。
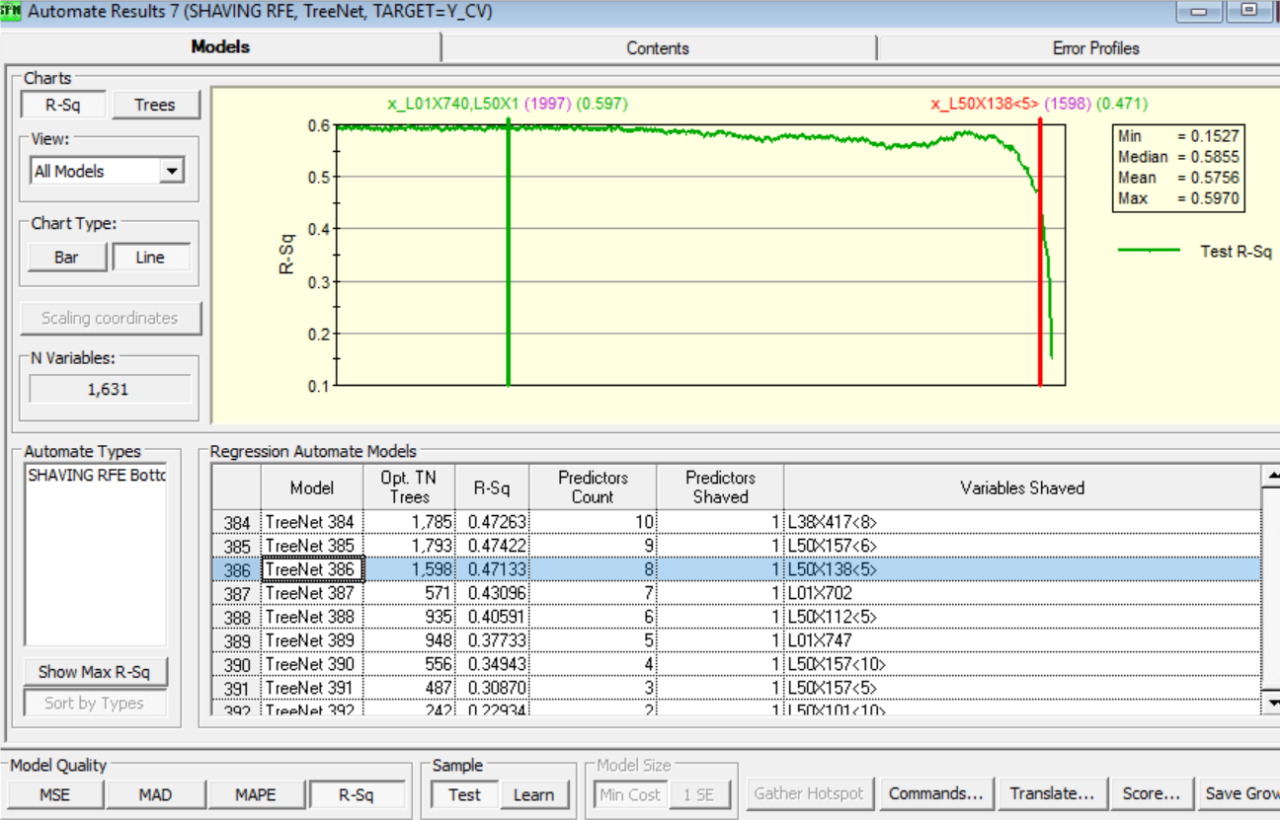
Russell 使用了 TreeNet 中的默认设置并调整了树的数量。当他着手剃除预测变量时,他开始了解它对检验 R 平方值的影响。
此颗粒大小控制模型仅有 8 个预测变量,但能说明检验样本中一半的变异。
为了找出这些关键变量背后真正的含义,Russell 使用了 SPM 的部分依赖图。某些变量落在了部分依赖曲线的陡峭位置,这揭示了它们的重要性。如果不使用 SPM 部分依赖曲线,那么可能无法发现这些变量的重要性。
然后,Russell 使用了一种直接的逐步方法。他每次从中剔除一个变量,然后观察对 R 平方产生的影响。起初并无任何重大改变,直到他剔除第四个最重要的变量。他将此变量告知制造团队并向他们了解此变量的更多信息。
成果
Russell 使用 SPM 的变量重要性排名功能将 1,000 多个预测变量迅速缩减到区区 8 个。而且单这 8 个预测变量就导致了检验样本中的近一半变异。
使用 SPM 的“从顶部剔除”功能,Russell 得以快速分辨出相较于其他任何变量而言对 R 平方的影响更显著的变量。最终证实此变量与结晶系统的原料流相关,但其对最终产品的影响在 Russell 创建 SPM 模型之前并不清晰。
之后,在 SPM 部分依赖图的帮助下,Russell 了解到了此变量对于颗粒大小不可靠性的影响很大。SPM 的部分依赖图展示了在“沿着分布曲线进行”更改时,此变量如何发生改变来响应这些更改。
“我们沿着此分布曲线的陡峭部分进行”,Russell 说道,“幸运的时候,变异系数会较低,而不那么幸运时,变异系数会较高。如果不使用 SPM,我永远也不会了解到这点”。
Russell 实现了他的目标,十分满意,他找到了几种方式来减小玉米葡萄糖晶体最终大小的变异,帮助食品制造商使用这些配料来改进销售给客户的产品。*该案例研究是在 2021 年推出 Minitab Engage 之前使用 Companion by Minitab 创建的。 收起阅读 »
半导体制造商提高质量和产量的 4 个步骤
半导体制造不仅是技术最先进的行业之一,而且也是成本最密集的行业之一。随着基于半导体的设备在从个人电脑到电话和汽车的一切事物中变得司空见惯,需求持续增长。随着数量的增加,对更强大的质量计划的需求也在增加。虽然大多数制造商都在使用 Minitab 等统计软件来解决某些问题,但仍有机会扩大其范围并提供更多价值。
半导体制造业往往比其他行业平均收集更多的数据。这意味着您可以更轻松地将数据以不同的方式发挥作用,例如:
使用测量系统分析最大限度地减少生产中的变化
使用量具 R&R 和方差分析等工具来确定测量系统的变化至关重要,尤其是对于半导体制造而言。为确保规格能够得到保证,测量的可重复性和再现性需要相对于测量的规格公差较小。 Minitab 的新测量系统分析 模块使各级从业人员能够轻松评估测量系统的变异、偏差和稳定性。
使用统计过程控制来提高产量并避免制造过程中的浪费
使用控制图和能力分析来测量关键特性,如晶圆厚度、沉积速率(晶圆表面沉积材料作为薄层以包含电气特性的速率)、终点时间(检测最准确的停止时间蚀刻工艺,以避免蚀刻过度或蚀刻不足)等将有助于确保您的工艺和设备处于可控状态。如果您已经在使用 SPC 方法,使用Minitab的 下一代统计过程控制可以帮助您改进技术并实现实时节省。
使用实验设计改进制造工艺
由于半导体制造由多个复杂的过程组成,即使是最有经验和能力的工程师也不一定知道制造设备的最佳设置。即使已知最佳设置,新技术也会不断被采用,从而引入未知情况和新问题。实验设计帮助工程师建立一个综合模型,以帮助非常准确地理解系统的工作原理。 通过阅读这篇博文,了解更多关于 DOE 的实际操作,帮助提高一个制造商抛光过程的均匀度,或者通过观看本次网络研讨会,了解更多关于 DOE 的总体信息。
使用机器学习进行硅后验证
与进行测量并做出通过/失败决策的生产测试不同,在硅后验证中,您需要非常详细地了解设备在各种操作条件下的行为。使用机器学习,您可以更好地了解设备的输入如何影响输出并找到它们之间隐藏的关系和复杂性。借助Minitab 的预测分析模块,您可以构建稳健的预测模型或使用我们的可变重要性图表等工具来突出显示影响性能的最关键输入。
收起阅读 »
半导体制造业往往比其他行业平均收集更多的数据。这意味着您可以更轻松地将数据以不同的方式发挥作用,例如:
使用测量系统分析最大限度地减少生产中的变化
使用量具 R&R 和方差分析等工具来确定测量系统的变化至关重要,尤其是对于半导体制造而言。为确保规格能够得到保证,测量的可重复性和再现性需要相对于测量的规格公差较小。 Minitab 的新测量系统分析 模块使各级从业人员能够轻松评估测量系统的变异、偏差和稳定性。
使用统计过程控制来提高产量并避免制造过程中的浪费
使用控制图和能力分析来测量关键特性,如晶圆厚度、沉积速率(晶圆表面沉积材料作为薄层以包含电气特性的速率)、终点时间(检测最准确的停止时间蚀刻工艺,以避免蚀刻过度或蚀刻不足)等将有助于确保您的工艺和设备处于可控状态。如果您已经在使用 SPC 方法,使用Minitab的 下一代统计过程控制可以帮助您改进技术并实现实时节省。
使用实验设计改进制造工艺
由于半导体制造由多个复杂的过程组成,即使是最有经验和能力的工程师也不一定知道制造设备的最佳设置。即使已知最佳设置,新技术也会不断被采用,从而引入未知情况和新问题。实验设计帮助工程师建立一个综合模型,以帮助非常准确地理解系统的工作原理。 通过阅读这篇博文,了解更多关于 DOE 的实际操作,帮助提高一个制造商抛光过程的均匀度,或者通过观看本次网络研讨会,了解更多关于 DOE 的总体信息。
使用机器学习进行硅后验证
与进行测量并做出通过/失败决策的生产测试不同,在硅后验证中,您需要非常详细地了解设备在各种操作条件下的行为。使用机器学习,您可以更好地了解设备的输入如何影响输出并找到它们之间隐藏的关系和复杂性。借助Minitab 的预测分析模块,您可以构建稳健的预测模型或使用我们的可变重要性图表等工具来突出显示影响性能的最关键输入。
收起阅读 »
控制图出现失控后一定要隔离产品和停线吗?
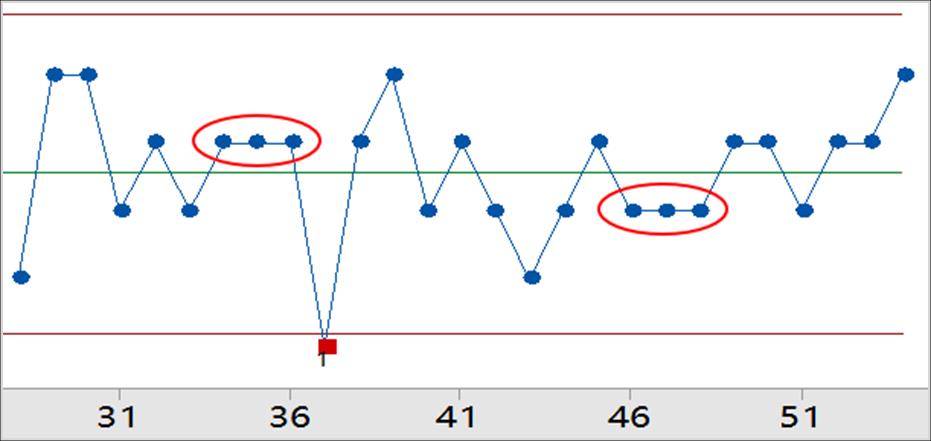
在我的前面的控制图相关文章中,讨论了控制图为什么能够发现失控的、子组大小的确定方法、判异与判稳的准则及其选择的依据等,而在控制图的实操过程中,还有一个避不开的问题,这就是:当发现失控时要对过程进行原因调查,那么还要必须隔离产品或者停线吗?
这是一个比较尖锐的问题,因为这关系到产品交付的及时性,会对相关部门的利益产生影响,尽管我们都是为了公司和客户着想。
是否需要隔离产品或者停线,取决于我们使用并出现下列判异准则中的哪几个:
准则1:1个点,距离中心线大于3个标准差
准则2:连续9个点,在中心线同一侧
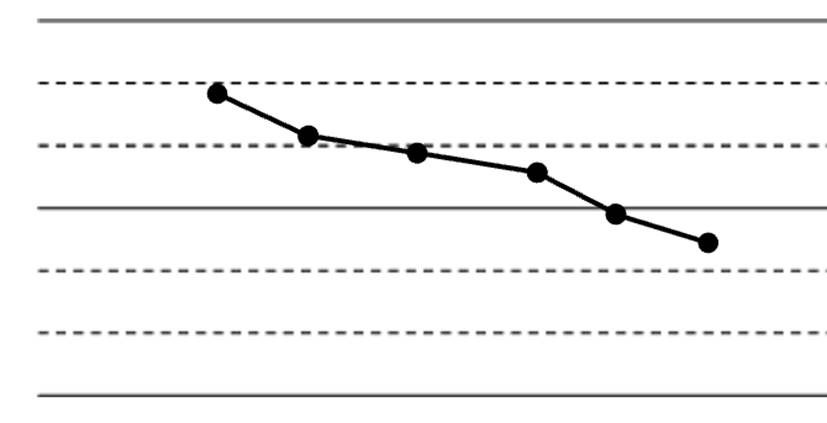
准则3:连续6个点,全部递增或全部递减
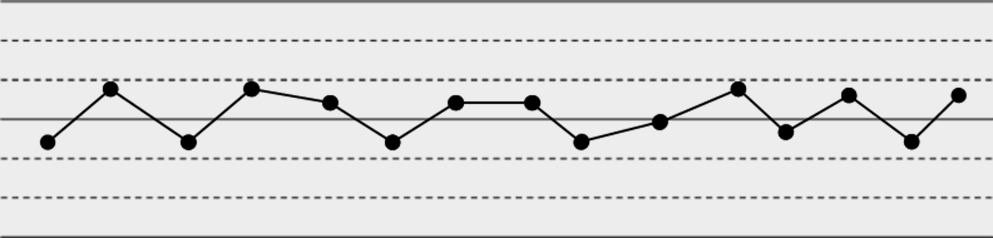
准则4:连续14个点,上下交错
准则5:3个点中有2个点,距离中心线(同侧)大于2个标准差
准则6:5个点中有4个点,距离中心线(同侧)大于1个标准差
准则7:连线15个点,距离中心线(任一侧)1个标准差以内准则8:连线8个点,距离中心线(任一侧)大于1个标准差判异准则1是必须使用的,我们就先讨论准则1。
均值点出界,又可分为两种情形:
情形1——均值点超出控制限,且超过规格限,是必须停线和隔离产品的,这是毫无疑问的,因为已经产生了不合格了,即使是过程特性,也意味着对应的产品特性大概率出现不合格。这种情形,我们就不进一步展开讨论了。
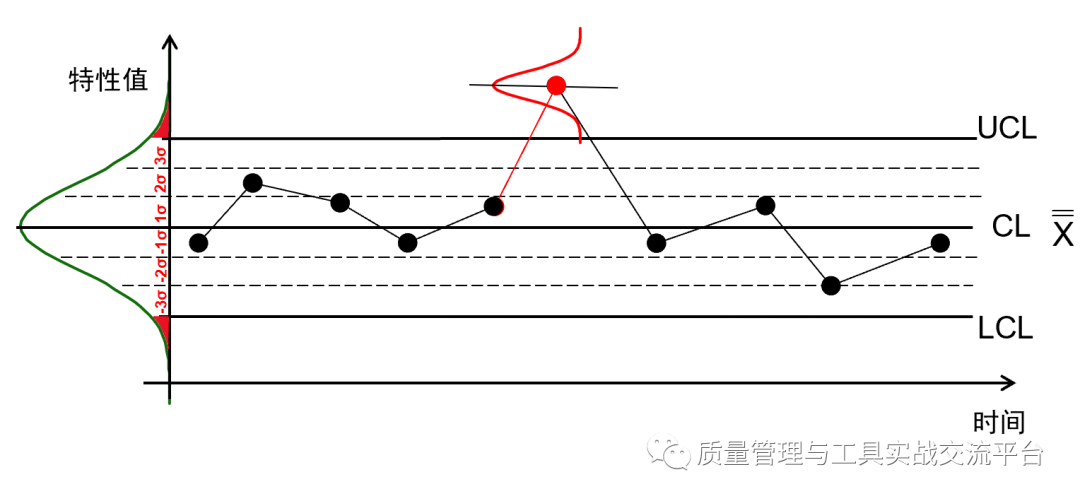
情形2——均值点超出控制限,但未超规格限。要知道未超规格限,只是我们所抽取的子组的均值未超规格限,这里面又可分为两种情况:子组内有个别单值可能会超规格限,这个容易确认,在测量样本时就知道了;另一种情况是在这个抽样时间段内,未抽到的产品特性可能还会有超规格,那么,如果有,会有多大的概率存在不合格呢?我们还是以最常用的均值-极差图为例。在均值图上出现了超界点,实际上就是均值发生了显著的偏移,不管是一种暂时性的偏移,还是永久性的。因为控制图的点是抽样所得,这个点就代表着抽样间隔内所生产的所有产品的特性值构成了一个新的分布,如下图所示,只是这个新的分布的均值与之前稳定时的分布均值有了显著的变异。
那么,我们现在来使用95%置信区间来估计超界均值点所代表的抽样时间间隔内的这个小的“总体均值”(后面叫做“抽样间隔总体”)是多少。
下面先简要介绍置信区间的概念。
由于不是100%检验,我们使用样本均值来对总体进行“点估计”,根据“中心极限定理”可知,样本均值等于总体的均值。但是由于总体均值是通过样本来估计的,所以总是存在抽样误差,这个误差就是:
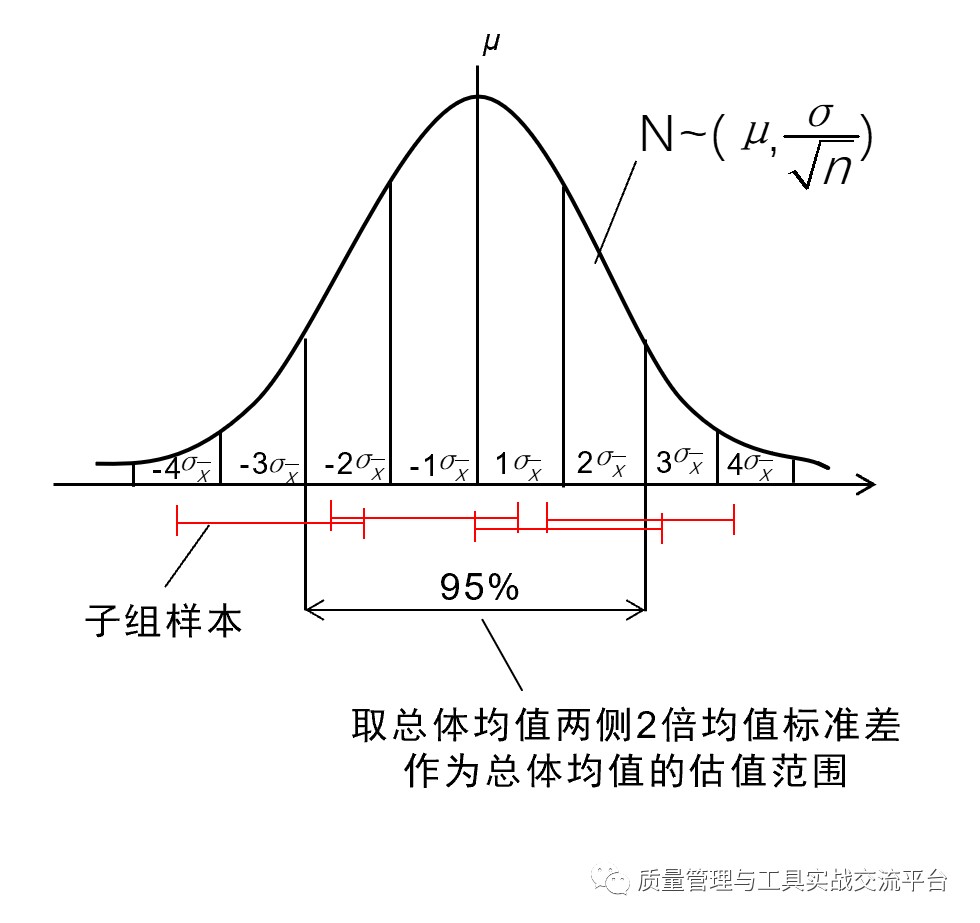
其中,σ 在本案例中是抽样时间段内特性单值的标准差,n 是每次抽样的数量。用子组样本均值估计抽样间隔总体均值存在上述抽样误差,同时这个抽样误差也是由(子组)样本均值所构成的正态分布的标准差,我们也把它叫做“标准误”。这个由均值点构成的正态分布的均值,就是我们要估计的“抽样间隔总体均值 μ”,如下图所示:
那么,我们就取正态布总体均值两侧2倍均值标准差,作为抽样间隔总体均值的估值范围,如上图所示,可见,这个范围正好占正态分布的95%,我们用下列95%置信区间公式来表达:
式中,μ 为样本均值,σ 为样本单值的标准差,n 为子组的大小,即抽样数量。
下一步,我们就看看特性的规格限是否落在了上述置信区间内,如果是,我们就可以说:抽样时间段内,有95%的可能性出现了不合格。
因此,准则1失控了,我们需要通过上述具体的计算,来评估产品的风险高低,做出是否隔离产品的决策,一旦隔离,就应进行全检。另外,判异准则1失控了,通常是需要停线来找原因的。
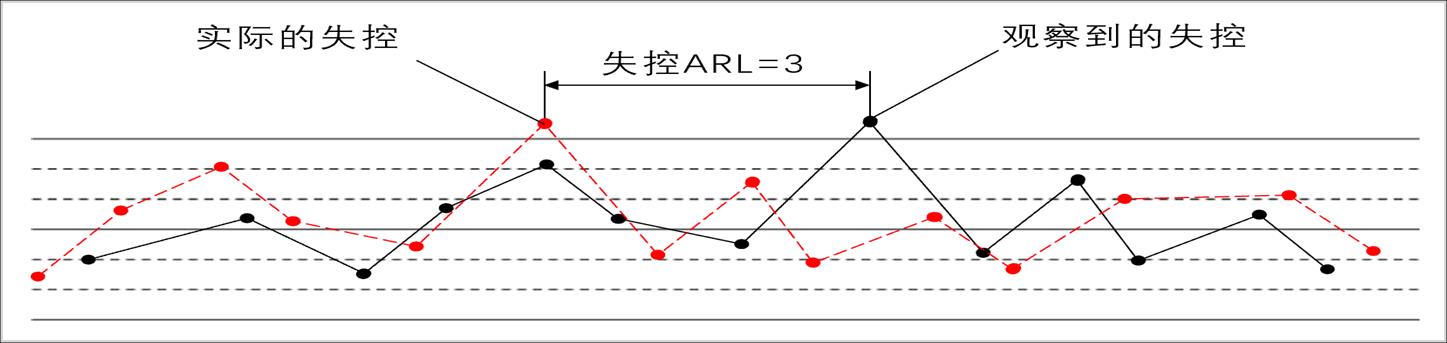
当需要隔离产品时,不能直接隔离一个最近一个抽样间隔的产品,还要根据具体的失控ARL来推算出实际失控的时间点在哪里,具体的原理,请详见我的另一篇文章“一个均值-极差控图子组大小的问题”,里面有详尽的介绍,就不在本文中赘述了。
准则5、6也属于均值偏移类型的失控,因此,是否隔离产品,也应通过上述的计算来做决策。
除了准则1、5、6以外,其他的准则,则属于趋势和点链了,出现不合格的可能性不大,只是调查原因即可。
下面我们再来讨论一下在极差图上出现超界点的问题。
极差图上出现超出下控制限的点,是子组的极差变小了,由此估计的产品的特性的标准差也就是离散度变小,这是我们所期望的,这往往是改善的结果。当极差图上出现超出上控制限的点时,就说明了子组样本特性的极差变大了,对应的产品特性间的标准差变大了,这就影响到了过程性能指数变大了,过程性能指数见下列公式:[图片]
我们需要从失控时开始,计算一下失控后具体过程的性能指数PPK,如果不能满足目标值,则应将产品隔离,进行全检。 收起阅读 »
这是一个比较尖锐的问题,因为这关系到产品交付的及时性,会对相关部门的利益产生影响,尽管我们都是为了公司和客户着想。
是否需要隔离产品或者停线,取决于我们使用并出现下列判异准则中的哪几个:
准则1:1个点,距离中心线大于3个标准差
准则2:连续9个点,在中心线同一侧
准则3:连续6个点,全部递增或全部递减
准则4:连续14个点,上下交错
准则5:3个点中有2个点,距离中心线(同侧)大于2个标准差
准则6:5个点中有4个点,距离中心线(同侧)大于1个标准差
准则7:连线15个点,距离中心线(任一侧)1个标准差以内准则8:连线8个点,距离中心线(任一侧)大于1个标准差判异准则1是必须使用的,我们就先讨论准则1。
均值点出界,又可分为两种情形:
情形1——均值点超出控制限,且超过规格限,是必须停线和隔离产品的,这是毫无疑问的,因为已经产生了不合格了,即使是过程特性,也意味着对应的产品特性大概率出现不合格。这种情形,我们就不进一步展开讨论了。
情形2——均值点超出控制限,但未超规格限。要知道未超规格限,只是我们所抽取的子组的均值未超规格限,这里面又可分为两种情况:子组内有个别单值可能会超规格限,这个容易确认,在测量样本时就知道了;另一种情况是在这个抽样时间段内,未抽到的产品特性可能还会有超规格,那么,如果有,会有多大的概率存在不合格呢?我们还是以最常用的均值-极差图为例。在均值图上出现了超界点,实际上就是均值发生了显著的偏移,不管是一种暂时性的偏移,还是永久性的。因为控制图的点是抽样所得,这个点就代表着抽样间隔内所生产的所有产品的特性值构成了一个新的分布,如下图所示,只是这个新的分布的均值与之前稳定时的分布均值有了显著的变异。
那么,我们现在来使用95%置信区间来估计超界均值点所代表的抽样时间间隔内的这个小的“总体均值”(后面叫做“抽样间隔总体”)是多少。
下面先简要介绍置信区间的概念。
由于不是100%检验,我们使用样本均值来对总体进行“点估计”,根据“中心极限定理”可知,样本均值等于总体的均值。但是由于总体均值是通过样本来估计的,所以总是存在抽样误差,这个误差就是:
其中,σ 在本案例中是抽样时间段内特性单值的标准差,n 是每次抽样的数量。用子组样本均值估计抽样间隔总体均值存在上述抽样误差,同时这个抽样误差也是由(子组)样本均值所构成的正态分布的标准差,我们也把它叫做“标准误”。这个由均值点构成的正态分布的均值,就是我们要估计的“抽样间隔总体均值 μ”,如下图所示:
那么,我们就取正态布总体均值两侧2倍均值标准差,作为抽样间隔总体均值的估值范围,如上图所示,可见,这个范围正好占正态分布的95%,我们用下列95%置信区间公式来表达:
式中,μ 为样本均值,σ 为样本单值的标准差,n 为子组的大小,即抽样数量。
下一步,我们就看看特性的规格限是否落在了上述置信区间内,如果是,我们就可以说:抽样时间段内,有95%的可能性出现了不合格。
因此,准则1失控了,我们需要通过上述具体的计算,来评估产品的风险高低,做出是否隔离产品的决策,一旦隔离,就应进行全检。另外,判异准则1失控了,通常是需要停线来找原因的。
当需要隔离产品时,不能直接隔离一个最近一个抽样间隔的产品,还要根据具体的失控ARL来推算出实际失控的时间点在哪里,具体的原理,请详见我的另一篇文章“一个均值-极差控图子组大小的问题”,里面有详尽的介绍,就不在本文中赘述了。
准则5、6也属于均值偏移类型的失控,因此,是否隔离产品,也应通过上述的计算来做决策。
除了准则1、5、6以外,其他的准则,则属于趋势和点链了,出现不合格的可能性不大,只是调查原因即可。
下面我们再来讨论一下在极差图上出现超界点的问题。
极差图上出现超出下控制限的点,是子组的极差变小了,由此估计的产品的特性的标准差也就是离散度变小,这是我们所期望的,这往往是改善的结果。当极差图上出现超出上控制限的点时,就说明了子组样本特性的极差变大了,对应的产品特性间的标准差变大了,这就影响到了过程性能指数变大了,过程性能指数见下列公式:[图片]
我们需要从失控时开始,计算一下失控后具体过程的性能指数PPK,如果不能满足目标值,则应将产品隔离,进行全检。 收起阅读 »
SPC控制图的判异与判稳
学习过SPC的朋友大都熟悉常规控制图的8大判异准则,这些判异准则详见我的前一篇文章“借助于PFMEA选择控制图判异准则”。控制图的判异是基于统计学中的“显著性检验”,例如,判异准则1——1个点,距离中心线超过3个标准差,也就是说,当过程受控时,只有0.27%的概率超过3个标准差,即I类错误(将受控误判为失控)的概率α=0.27%,是小概率事件,若真的超过了,就说明过程真的失控了。反过来讲,如果这一个点位于3个标准差之内,就可以说过程稳定受控吗?这样讲对吗?
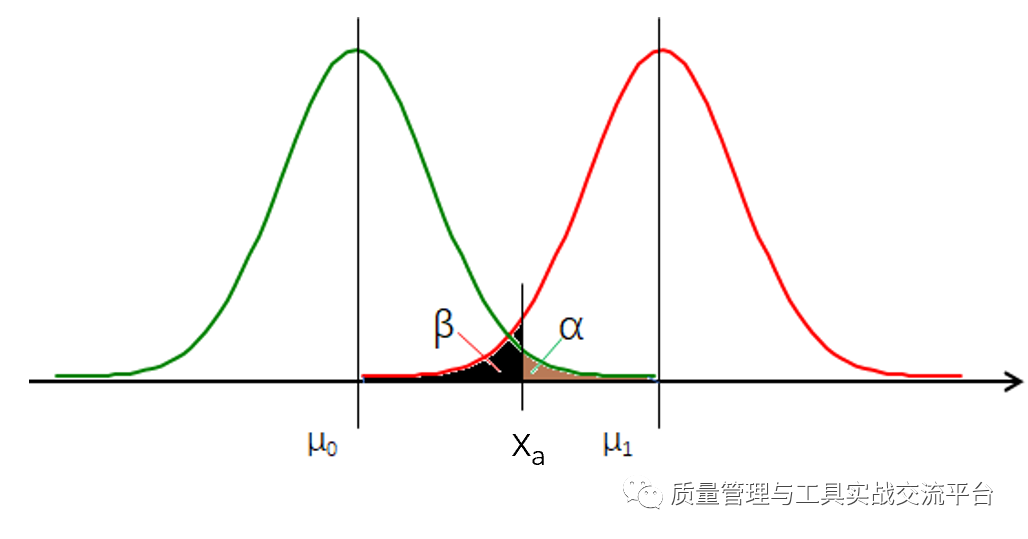
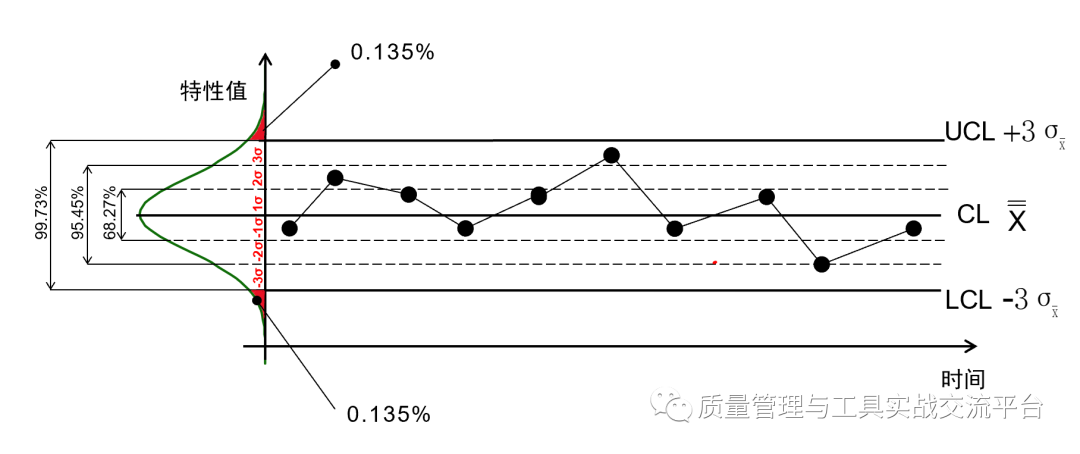
从统计学上来讲,如是I类错误α的概率很小,则II类错误(将失控误判为受控)β的概率将很大,如下图所示,左边的绿色分布图代表着受控时点的概率分布,右边的红色分布图代表着失控时点的概率分布,Xa是临界点,相当于控制图的控制限,如果Xa向右移,则α将会变小,而β将会变大。因此,如果是只用1个点在正负3倍标准差范围内作为判断过程受控的基准,这将会有过高的II类错误的风险。
故,我们不能只使用1个点来判断过程是否受控,但可以使用多个连续的点来进行判断,这是因为多个,例如n个连续的点在一起的II类风险概率将是βn,基于这个理论,规定了以下3个判稳准则,符合任何一个,就可以认为过程受控:
(1)连续25个点子都在控制界限内;
(2)连续35个点子至多1个点子落在控制界限外;
(3)连续100个点子至多2个点子落在控制界限外。
我们分别计算一下这3条准则的α:
对于准则2:当过程受控的时候,连续35个点中,至多1个点落在控制界限外的概率为:
故
也就是说,如果使用判稳准则2,则只有0.41%的概率将受控误判为失控,这与判异准则1中的0.27%处于同一个数量级上。
同样的方法,我们还可以得到判稳准则1和3的α:
α1=6.54%,α3=0.26%,
其中,准则1的I类风险还是比较高的,因此,有的专家认为可以不使用准则1。
可见这3条准则的I类风险是依次递减的,但这3条准则所需要的样本数量是依次递增的,成本也是递增的。为此,可以按照下列程序来使用:
使用判稳准则1,若不能判稳,则使用准则2;
使用判稳准则2,若还不能判稳,则使用准则3;
使用判稳准则3,仍不能判稳,则应停止使用判稳准则。
当出现界外点时,我们必须调查原因,确认是特殊原因造成的,还是属于I类错误,如果是特殊原因造成的,则应对过程进行改进,使其回到稳态。
现在,我们已经学习了判异准则和判稳准则,接下来的问题是:什么时候使用判稳准则,什么时候使用判异准则呢?
判稳准则,就是用来判断过程是否是稳定受控的,这正好适用于控制图的第一阶段——分析阶段控制图。控制图的分析阶段的任务是通过有限的样本建立控制限,而控制限在用于第二阶段——控制阶段之前,必须满足2个条件:1)过程必须是稳定的;2)过程的能力是足够的。一般情况下,是通过抽取25个子组,即通过25点来建立控制限的,因此我们可以先使用判稳准则1——连续25个点没有超过控制限,来判断过程是否稳定。当然 ,为了更加有信心,我们可以使用准则2或者准则3。
在控制图的正式使用的过程中(控制阶段),我们首先使用判异准则1,若发现有1点超限,则有两种可能:1)存在特殊原因;2)属于判异准则1的α错误。在调查原因后,如果没有发现特殊原因,我们就可以从那个超限的点开始,再使用判稳准则来判断过程是否真的没有失控。
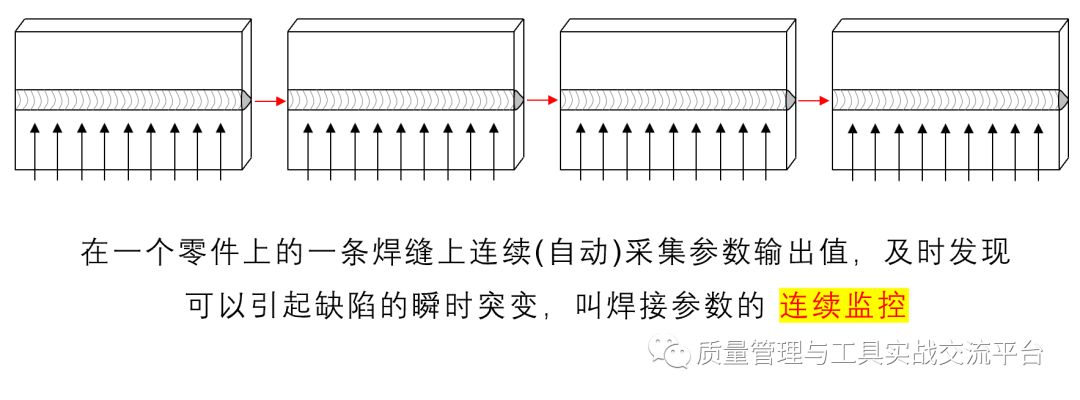
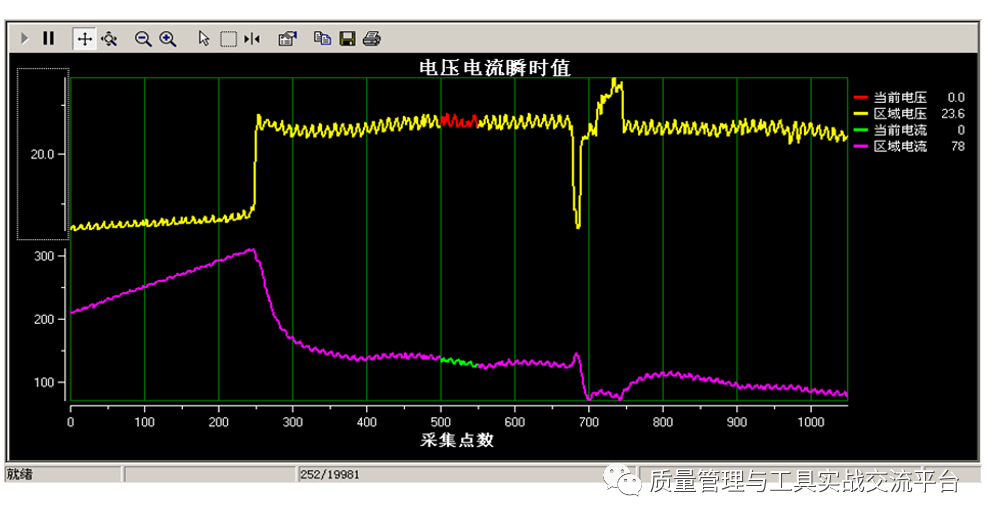
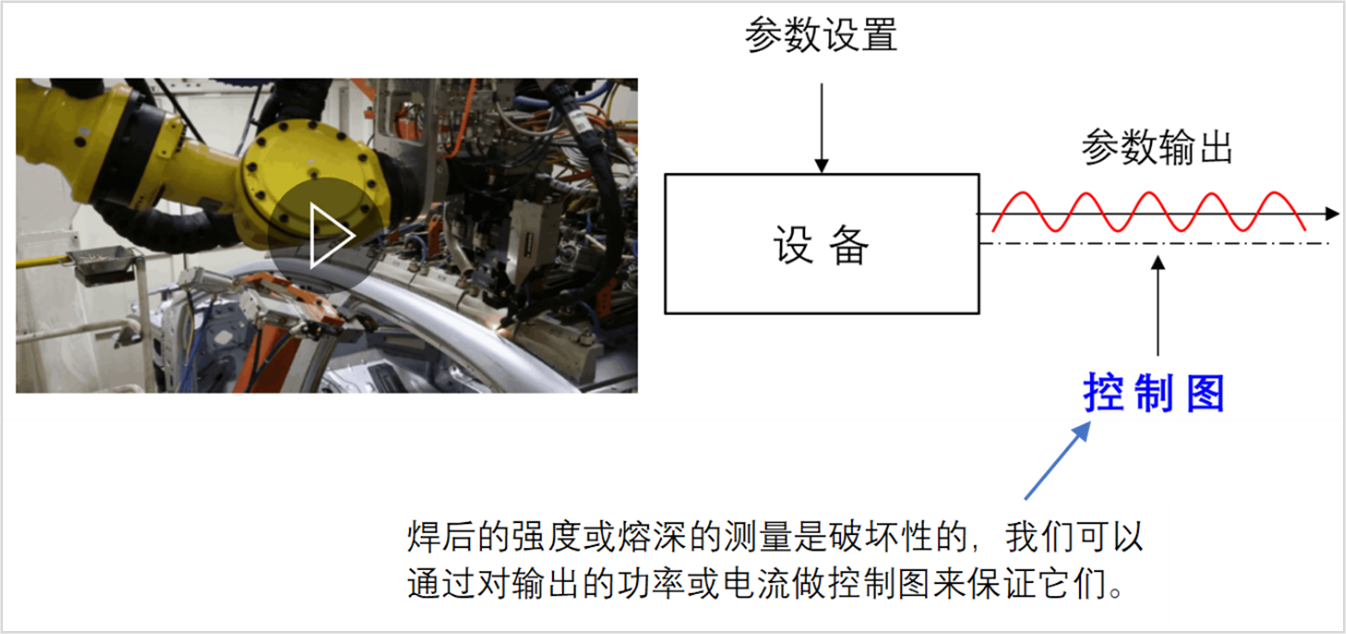
当然,出现超限点而找不到原因,也会存在这样的一种可能:过程出现了NTF原因,即不能够再现的原因,只是偶尔出现过一次,随后又恢复了正常,当我们去调查时,一切正常,不留任何痕迹。对于这种类型的问题,依赖于周期性抽样的控制图就不适用了!我们应当导入连续采样系统,与零件的序列号关联,进行连续监控、实时报警和追溯。这种系统的采样周期是很短的,如焊接电流的输出采样,采样周期可达几十毫秒,这属于大数据控制的范畴了,如下图所示。
收起阅读 »
从统计学上来讲,如是I类错误α的概率很小,则II类错误(将失控误判为受控)β的概率将很大,如下图所示,左边的绿色分布图代表着受控时点的概率分布,右边的红色分布图代表着失控时点的概率分布,Xa是临界点,相当于控制图的控制限,如果Xa向右移,则α将会变小,而β将会变大。因此,如果是只用1个点在正负3倍标准差范围内作为判断过程受控的基准,这将会有过高的II类错误的风险。
故,我们不能只使用1个点来判断过程是否受控,但可以使用多个连续的点来进行判断,这是因为多个,例如n个连续的点在一起的II类风险概率将是βn,基于这个理论,规定了以下3个判稳准则,符合任何一个,就可以认为过程受控:
(1)连续25个点子都在控制界限内;
(2)连续35个点子至多1个点子落在控制界限外;
(3)连续100个点子至多2个点子落在控制界限外。
我们分别计算一下这3条准则的α:
对于准则2:当过程受控的时候,连续35个点中,至多1个点落在控制界限外的概率为:
故
也就是说,如果使用判稳准则2,则只有0.41%的概率将受控误判为失控,这与判异准则1中的0.27%处于同一个数量级上。
同样的方法,我们还可以得到判稳准则1和3的α:
α1=6.54%,α3=0.26%,
其中,准则1的I类风险还是比较高的,因此,有的专家认为可以不使用准则1。
可见这3条准则的I类风险是依次递减的,但这3条准则所需要的样本数量是依次递增的,成本也是递增的。为此,可以按照下列程序来使用:
使用判稳准则1,若不能判稳,则使用准则2;
使用判稳准则2,若还不能判稳,则使用准则3;
使用判稳准则3,仍不能判稳,则应停止使用判稳准则。
当出现界外点时,我们必须调查原因,确认是特殊原因造成的,还是属于I类错误,如果是特殊原因造成的,则应对过程进行改进,使其回到稳态。
现在,我们已经学习了判异准则和判稳准则,接下来的问题是:什么时候使用判稳准则,什么时候使用判异准则呢?
判稳准则,就是用来判断过程是否是稳定受控的,这正好适用于控制图的第一阶段——分析阶段控制图。控制图的分析阶段的任务是通过有限的样本建立控制限,而控制限在用于第二阶段——控制阶段之前,必须满足2个条件:1)过程必须是稳定的;2)过程的能力是足够的。一般情况下,是通过抽取25个子组,即通过25点来建立控制限的,因此我们可以先使用判稳准则1——连续25个点没有超过控制限,来判断过程是否稳定。当然 ,为了更加有信心,我们可以使用准则2或者准则3。
在控制图的正式使用的过程中(控制阶段),我们首先使用判异准则1,若发现有1点超限,则有两种可能:1)存在特殊原因;2)属于判异准则1的α错误。在调查原因后,如果没有发现特殊原因,我们就可以从那个超限的点开始,再使用判稳准则来判断过程是否真的没有失控。
当然,出现超限点而找不到原因,也会存在这样的一种可能:过程出现了NTF原因,即不能够再现的原因,只是偶尔出现过一次,随后又恢复了正常,当我们去调查时,一切正常,不留任何痕迹。对于这种类型的问题,依赖于周期性抽样的控制图就不适用了!我们应当导入连续采样系统,与零件的序列号关联,进行连续监控、实时报警和追溯。这种系统的采样周期是很短的,如焊接电流的输出采样,采样周期可达几十毫秒,这属于大数据控制的范畴了,如下图所示。
收起阅读 »
借助于PFMEA选择控制图判异准则
前言:熟悉SPC控制图的朋友一般都知道,常规控制图有8个判异准则,在AIAG发布的《SPC参考手册》第二版中(英文版P75)特别提到,除了准则1(一个点,距离中心线超过3个标准差)必须使用外,其他准则的应用没有优先级,应当根据实际过程特性的特点来选用。用的判异准则越多,那么犯第I类错误的机会也越大,也就是说,会有更多的机会把实际上受控的过程,判断为失控,即误报警。为什么使用的准则越多,误报警的机会越多?这个概率有多大?我们到底应当依据什么来选择判异准则?那么,本文就来对这些疑问进行探讨。
下面是常规控制图的8个判异准则:
准则1:1个点,距离中心线大于3个标准差
准则2:连续9个点,在中心线同一侧
准则3:连续6个点,全部递增或全部递减
准则4:连续14个点,上下交错
准则5:3个点中有2个点,距离中心线(同侧)大于2个标准差
准则6:5个点中有4个点,距离中心线(同侧)大于1个标准差
准则7:连线15个点,距离中心线(任一侧)1个标准差以内
准则8:连线8个点,距离中心线(任一侧)大于1个标准差。
在使用(On-going)控制图进行过程控制时,只要出现上述模式的点,就判断为失控。
然而,我们还要明白:即使过程处于统计受控的状态之中,仍然有机会出现上述情况,只不过每一种情况出现的概率很小,属于“小概率事件”。
例如,准则1:在过程受控时,均值图中的点构成正态分布,我们通常使用正态分布中离均值两侧3倍标准差的地方为控制限,如下图所示,那么点子超出控制限一侧的概率为0.135%,也就是说,即使过程统计受控,它也会有0.135%的误报警概率!
我们再看准则2:在过程受控时,控制图中连续9点位于中心线同一侧的概率为2×(1/2)^(9)=0.00391,也就是说会有0.391%的误报警概率。
假设我们全部使用上述8条准则,则即使过程稳定受控,也会有2.373%的误报警率!
误报警,会给我们的正常生产带来不必要的成本损失,而且停线了也找不到报警的原因,最后会使人们对SPC控制图这个工具产生质疑,甚至弃用!
因此,使用的判异准则并不是越多越好,而是应当根据所控过程特性的特点来选择使用。那么,我们应当依据什么来选择控制图的判异准则呢?
我们需要事先对所要控制的过程和特性做一个深入的研究,而能够帮助我们做出深入研究的工具,就是PFMEA!
PFMEA,可以帮助我们全面认识所控过程的失效模式及其失效起因,我们就会提前知道当某种失效起因存在时,它所导致的失效模式,或者失效起因,在控制图上会以一种什么方式显现,这样就可以选择与其对应的那条判异准则。下面我们通过几个示例来说明一下。
在此还需要说明一下:如果在PFMEA的优化措施之后,失效起因对应的发生频度O很小,则可以不用考虑对应的判异准则。
请注意:为了使内容显得紧凑、重点突出,下面的系列示例中,特使用《FMEA参考手册》第四版的表格格式,只写出部分失效模式,且只写到失效起因,其余信息在此略去。
示例1:“变速箱输出轴加工\冷车削”的PFMEA分析的部分内容
在本示例中,我们可以使用2个控制图监控2个产品特性:“密封面外径”和“圆柱外径”,除了使用准则1外,我们还可以根据它们的失效起因来选择其他准则。对于密封面外径大这个失效模式,它有2个潜在失效起因,起因1—进给量设置过小,它导致失效时对应的判异准则应当是准则2,且可能是出现在均值图上,即连续9个点(以上)位置中心线的上侧。
起因2—刀具硬度过低,磨损严重,它导致失效时所对应的判异准则,应当是准则3,且可能是出现在均值图上,即连续6个点(以上)上升,这是因为刀具磨损是一个逐渐恶化的过程,越磨,刀具磨损的就越多,则轴密封面的外径就越大。同时,它还可能导致极差图上有点超过上控制限。
对于密封面外径过小这个失效模式,它有1个潜在失效起因,就是进给量设置过大,它导致的失效模式对应的异准则,是准则2。
圆柱外径的失效模式,分析内容同密封面外径的失效模式,在此略。
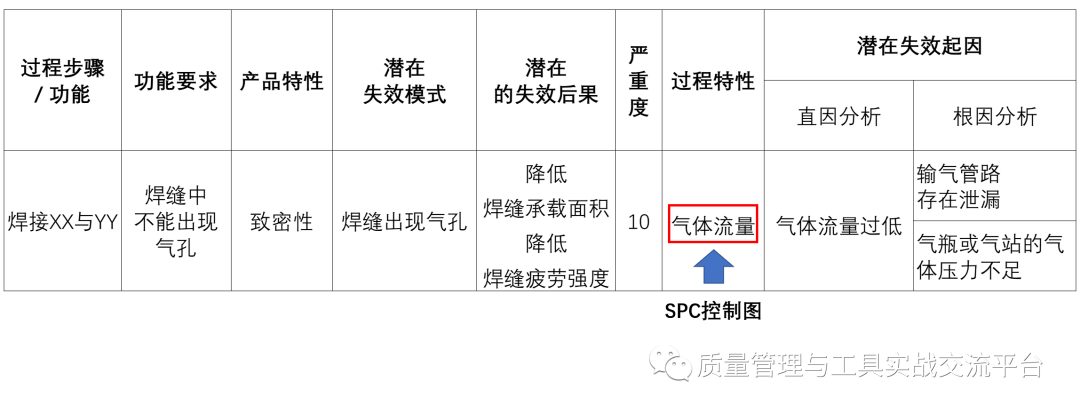
示例2:“气体保护焊”的PFMEA分析的部分内容
我们可以对过程特性“气体流量”来使用控制图进行监控,不过,由于从流量计读出的流量数据随时间的变化不敏感,因此,它适用于单值-移动极差控制图,而这种控制图的失控判断准则,只有准则1适用(该结论来源于《SPC参考手册》第二版英文版P87)。不过,从理论来讲,如果单值数据符合正态分布,则可以适用于其他准则。
如果是由于输气管泄漏或者气瓶/气站压力不足而引起的流量不足,也会呈现出单值图上连续6点或以上下降的模式。
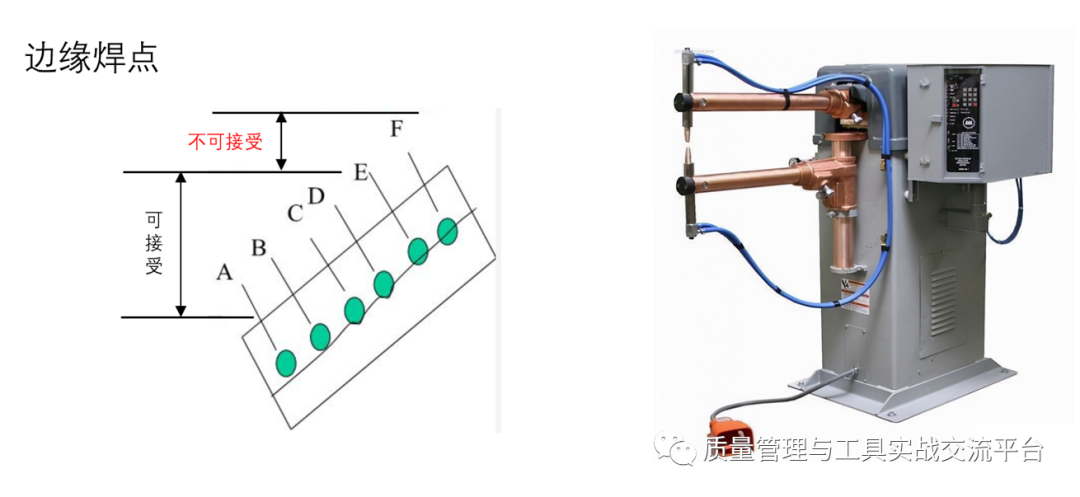
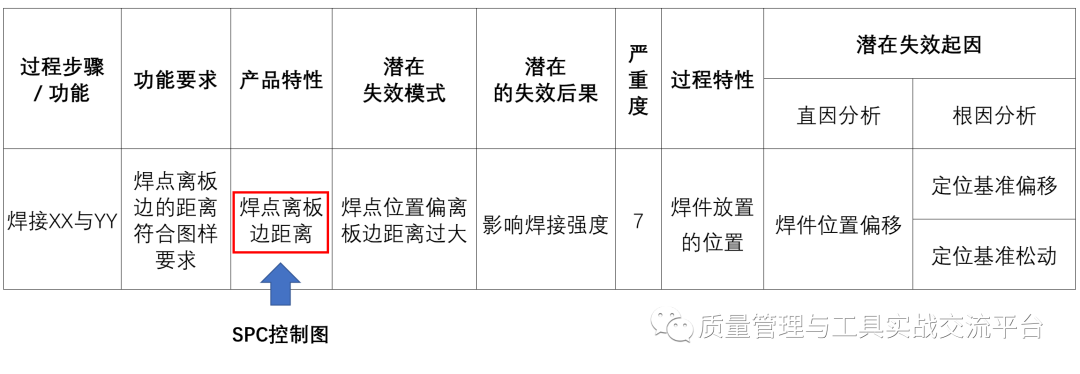
示例3:“电阻点焊”的PFMEA分析的部分内容
如果对焊点离板边距离做控制图,建议只使用偏离最严重的那个点的数据,可以使用均值-极差控制图。
如果是由于“定位基准偏移”造成了焊点位置偏离板边距离过大,那么,除了准则1外,在均值图上将会出现与准则2对应的模式,即连续9点在中心线一侧。
如果是由于“定位基准松动”的原因,那么,在极差图上会有准则1的模式。
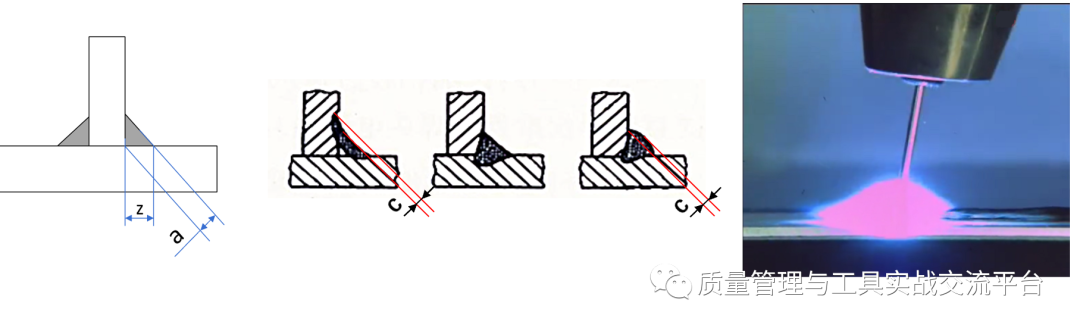
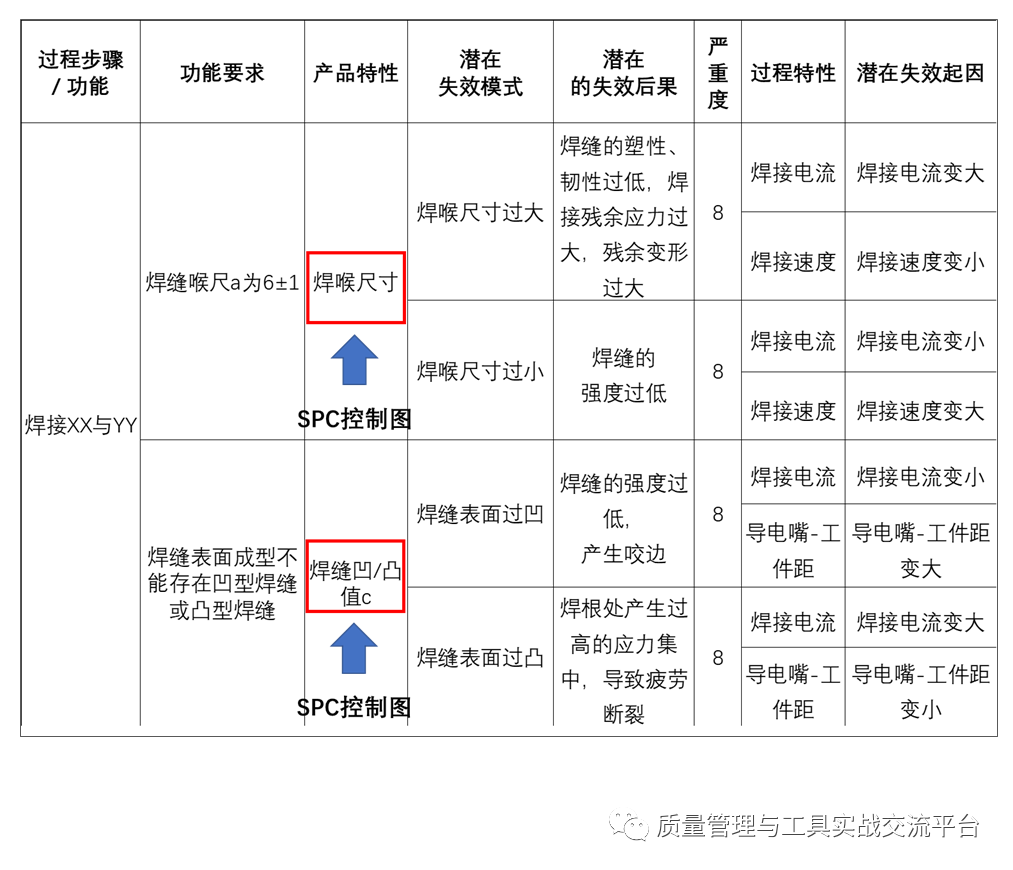
示例4:“熔化焊过程”的PFMEA分析的部分内容
我们可以针对焊喉尺寸a和焊缝凹凸值c,如上图所示,分别做控制图进行监控。由于a和z均可通过专用焊缝测量尺进行无损测量,如下图所示,可以方便地获得大量样本,过程稳定受控时,a值和z值各自符合正态分布,c值是通过减法运算得到的,故c值也符合正态分布,因此,可以使用均值-极差控制图。
对于焊喉尺寸a,影响a值的焊接电流、焊接速度的变化,属于偏移,而不属于波动,因为瞬时的波动通常会引起未焊透或熔深的波动,而不会引起焊缝尺寸上的变化,而偏移一段时间,则会得到过大或过小的焊缝尺寸值,故所对应的控制图的失控判异准则,除了准则1外,还应选择准则2,即连续9点在中心线一侧。
对于焊缝凹凸值c,影响c值的焊接电流、导电嘴-工件距的变化,属于偏移,而不属于波动,与a的情况相同,因此,除准则1外,也可以选择准则9。
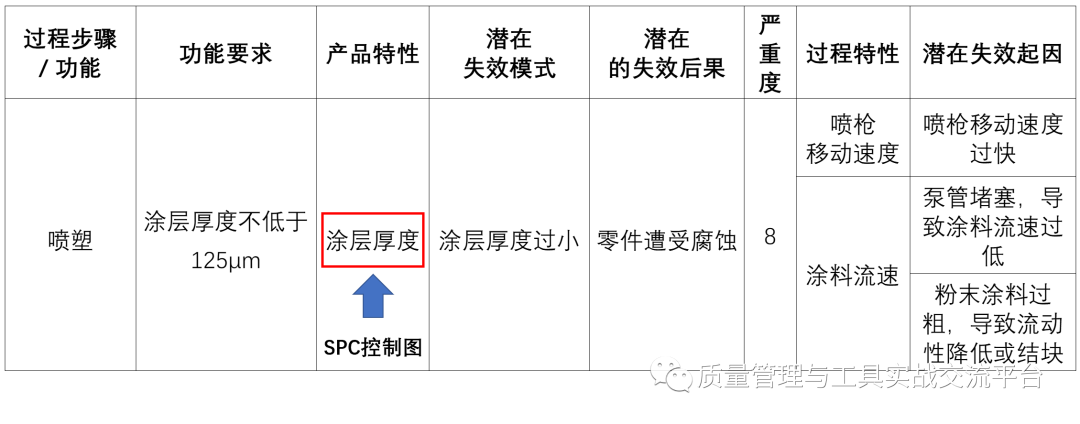
示例5:“静电喷涂”过程的PFMEA分析的部分内容
我们对“涂层厚度”做控制图进行监控,使用测厚仪进行测量,可以使用均值-极差控制图。
对于涂层厚度过小的影响因素—喷枪移动速度,则会存在速度总体偏快的情况,那么对应的控制图判异准则除了1外,对于均值图,可使用准则2;如果是手工喷涂,则还存在速度时快时慢的问题,反映到极差图上,则会有过高的极差点,故应使用准则1。
对于泵管堵塞这个失效起因,堵塞会越堵越厉害,它会引起涂料的在管内的滞留和堆积,使得流速越来低,导致涂层厚度越来越小,那么对应的判异准则,除1外,还有3,即连续6点下降。
对于涂料粉末过粗,流动性过低,则会使涂层厚度整体减小, 即对应准则2(除使用准则1外)。
示例6:“扫描仪组装”的PFMEA分析的部分内容
我们对无尘室离子浓度使用控制图进行监控,但是离子浓度的测量值不适合使用均值-极差图,而适用于单值-移动极差图,因此,根据SPC参考手册的要求,一般只用准则1。
但是,如果我们验证测量值确实符合正态分布,那么也可以使用其他准则。如果是无尘室有泄漏,则室内的离子浓度会越来越高,因此会在单值图上呈现出准则3的模式;如果是无尘室的吸尘器功能减弱,则在单值图上会呈现出准则2所描述的模式。
以上是通过6个示例,从不同的应用领域和行业,说明了如何借助于PFMEA来选择控制图以及控制图的判异准则,也由此可以看出,工具是相互联系的,我们应当做到将不同的工具进行联合应用,这样才能真正切合工作实际,真正解决实际问题! 收起阅读 »
下面是常规控制图的8个判异准则:
准则1:1个点,距离中心线大于3个标准差
准则2:连续9个点,在中心线同一侧
准则3:连续6个点,全部递增或全部递减
准则4:连续14个点,上下交错
准则5:3个点中有2个点,距离中心线(同侧)大于2个标准差
准则6:5个点中有4个点,距离中心线(同侧)大于1个标准差
准则7:连线15个点,距离中心线(任一侧)1个标准差以内
准则8:连线8个点,距离中心线(任一侧)大于1个标准差。
在使用(On-going)控制图进行过程控制时,只要出现上述模式的点,就判断为失控。
然而,我们还要明白:即使过程处于统计受控的状态之中,仍然有机会出现上述情况,只不过每一种情况出现的概率很小,属于“小概率事件”。
例如,准则1:在过程受控时,均值图中的点构成正态分布,我们通常使用正态分布中离均值两侧3倍标准差的地方为控制限,如下图所示,那么点子超出控制限一侧的概率为0.135%,也就是说,即使过程统计受控,它也会有0.135%的误报警概率!
我们再看准则2:在过程受控时,控制图中连续9点位于中心线同一侧的概率为2×(1/2)^(9)=0.00391,也就是说会有0.391%的误报警概率。
假设我们全部使用上述8条准则,则即使过程稳定受控,也会有2.373%的误报警率!
误报警,会给我们的正常生产带来不必要的成本损失,而且停线了也找不到报警的原因,最后会使人们对SPC控制图这个工具产生质疑,甚至弃用!
因此,使用的判异准则并不是越多越好,而是应当根据所控过程特性的特点来选择使用。那么,我们应当依据什么来选择控制图的判异准则呢?
我们需要事先对所要控制的过程和特性做一个深入的研究,而能够帮助我们做出深入研究的工具,就是PFMEA!
PFMEA,可以帮助我们全面认识所控过程的失效模式及其失效起因,我们就会提前知道当某种失效起因存在时,它所导致的失效模式,或者失效起因,在控制图上会以一种什么方式显现,这样就可以选择与其对应的那条判异准则。下面我们通过几个示例来说明一下。
在此还需要说明一下:如果在PFMEA的优化措施之后,失效起因对应的发生频度O很小,则可以不用考虑对应的判异准则。
请注意:为了使内容显得紧凑、重点突出,下面的系列示例中,特使用《FMEA参考手册》第四版的表格格式,只写出部分失效模式,且只写到失效起因,其余信息在此略去。
示例1:“变速箱输出轴加工\冷车削”的PFMEA分析的部分内容
在本示例中,我们可以使用2个控制图监控2个产品特性:“密封面外径”和“圆柱外径”,除了使用准则1外,我们还可以根据它们的失效起因来选择其他准则。对于密封面外径大这个失效模式,它有2个潜在失效起因,起因1—进给量设置过小,它导致失效时对应的判异准则应当是准则2,且可能是出现在均值图上,即连续9个点(以上)位置中心线的上侧。
起因2—刀具硬度过低,磨损严重,它导致失效时所对应的判异准则,应当是准则3,且可能是出现在均值图上,即连续6个点(以上)上升,这是因为刀具磨损是一个逐渐恶化的过程,越磨,刀具磨损的就越多,则轴密封面的外径就越大。同时,它还可能导致极差图上有点超过上控制限。
对于密封面外径过小这个失效模式,它有1个潜在失效起因,就是进给量设置过大,它导致的失效模式对应的异准则,是准则2。
圆柱外径的失效模式,分析内容同密封面外径的失效模式,在此略。
示例2:“气体保护焊”的PFMEA分析的部分内容
我们可以对过程特性“气体流量”来使用控制图进行监控,不过,由于从流量计读出的流量数据随时间的变化不敏感,因此,它适用于单值-移动极差控制图,而这种控制图的失控判断准则,只有准则1适用(该结论来源于《SPC参考手册》第二版英文版P87)。不过,从理论来讲,如果单值数据符合正态分布,则可以适用于其他准则。
如果是由于输气管泄漏或者气瓶/气站压力不足而引起的流量不足,也会呈现出单值图上连续6点或以上下降的模式。
示例3:“电阻点焊”的PFMEA分析的部分内容
如果对焊点离板边距离做控制图,建议只使用偏离最严重的那个点的数据,可以使用均值-极差控制图。
如果是由于“定位基准偏移”造成了焊点位置偏离板边距离过大,那么,除了准则1外,在均值图上将会出现与准则2对应的模式,即连续9点在中心线一侧。
如果是由于“定位基准松动”的原因,那么,在极差图上会有准则1的模式。
示例4:“熔化焊过程”的PFMEA分析的部分内容
我们可以针对焊喉尺寸a和焊缝凹凸值c,如上图所示,分别做控制图进行监控。由于a和z均可通过专用焊缝测量尺进行无损测量,如下图所示,可以方便地获得大量样本,过程稳定受控时,a值和z值各自符合正态分布,c值是通过减法运算得到的,故c值也符合正态分布,因此,可以使用均值-极差控制图。
对于焊喉尺寸a,影响a值的焊接电流、焊接速度的变化,属于偏移,而不属于波动,因为瞬时的波动通常会引起未焊透或熔深的波动,而不会引起焊缝尺寸上的变化,而偏移一段时间,则会得到过大或过小的焊缝尺寸值,故所对应的控制图的失控判异准则,除了准则1外,还应选择准则2,即连续9点在中心线一侧。
对于焊缝凹凸值c,影响c值的焊接电流、导电嘴-工件距的变化,属于偏移,而不属于波动,与a的情况相同,因此,除准则1外,也可以选择准则9。
示例5:“静电喷涂”过程的PFMEA分析的部分内容
我们对“涂层厚度”做控制图进行监控,使用测厚仪进行测量,可以使用均值-极差控制图。
对于涂层厚度过小的影响因素—喷枪移动速度,则会存在速度总体偏快的情况,那么对应的控制图判异准则除了1外,对于均值图,可使用准则2;如果是手工喷涂,则还存在速度时快时慢的问题,反映到极差图上,则会有过高的极差点,故应使用准则1。
对于泵管堵塞这个失效起因,堵塞会越堵越厉害,它会引起涂料的在管内的滞留和堆积,使得流速越来低,导致涂层厚度越来越小,那么对应的判异准则,除1外,还有3,即连续6点下降。
对于涂料粉末过粗,流动性过低,则会使涂层厚度整体减小, 即对应准则2(除使用准则1外)。
示例6:“扫描仪组装”的PFMEA分析的部分内容
我们对无尘室离子浓度使用控制图进行监控,但是离子浓度的测量值不适合使用均值-极差图,而适用于单值-移动极差图,因此,根据SPC参考手册的要求,一般只用准则1。
但是,如果我们验证测量值确实符合正态分布,那么也可以使用其他准则。如果是无尘室有泄漏,则室内的离子浓度会越来越高,因此会在单值图上呈现出准则3的模式;如果是无尘室的吸尘器功能减弱,则在单值图上会呈现出准则2所描述的模式。
以上是通过6个示例,从不同的应用领域和行业,说明了如何借助于PFMEA来选择控制图以及控制图的判异准则,也由此可以看出,工具是相互联系的,我们应当做到将不同的工具进行联合应用,这样才能真正切合工作实际,真正解决实际问题! 收起阅读 »
不会作假就搞不了质量体系,五大工具只忽悠中国人?(转)
看到一个帖子,标题是这样的:
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
你的感受如何?
当你知道这句话是总经理对刚入职的体系经理说的,感受又如何?
搞质量体系的,自然也离不开质量工具,说到质量工具的绕不开的当然是五大工具。
五大工具太有名了。有名到如果你不知道它们,都不好意思说自己是在汽车行业混的。虽说不是强制性要求,可并不妨碍各大主机厂对它们的推崇,进行影响着整个汽车行业。
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
它们分别是:
APQP 产品质量先期策划 Advanced Product Quality Planning
FMEA 潜在失效模式及后果分析 Failure Mode & Effect Analyse
MSA 测量系统分析 Measurement System Analyse
SPC 统计过程控制 Statistical Process Control
PPAP 生产件批准程序 Production Part Approval Process
这五大手册源自于美国QS9000质量体系,是三大汽车公司克来斯勒、福特和通用制定的对其供方的标准质量要求。
不过,名气大了,就显得有些“高冷”,很多朋友在学习五大手册的时候总觉得有些高深难懂。 甚至有人说 五大工具只会忽悠中国人,公司里 搞体系的在带头造假!
是这个情况吗?
今天应审指挥部分享一篇关于五大工具中SPC的 深度解读文章 。
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
当然,这里还是要简单介绍一下,S PC 统计过程控制 的研究对象其实只有一个,就是过程!
通过统计分析技术对生产过程(注意MSA的对象是测量系统)进行实时监控,科学的区分出生产过程中产品质量的随机波动与异常波动,从而对生产过程的异常趋势提出预警,以便生产管理人员及时采取措施,消除异常,恢复过程的稳定,从而达到提高和控制质量的目的。
简单说来,SPC的通过控制好各种过程(核心是生产过程),最终生产出来的产品质量稳定。 文章有点长,不过满满干货,性价比绝对杠杠的,一起来看看吧。
01
前言
1924年,休哈特带着他的控制图“问世”之后,被以汽车行业为代表的制造业,广泛用来监控和改进生产过程,试图通过产品质量特性变化趋势来进行质量预防,改变旧有的事后质量检验的方式,来降低质量成本,并被列入汽车行业质量管理五大工具之一。
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
其实,在以美国为代表的制造业强国中,不论是统计专家还是质量专家,针对SPC的实用性以及有效性的思考和质疑之声,从来就没停止过。
日本更是以实际效用为准绳,而不是在实际推广中原封不动地照搬照抄SPC。
对于SPC的质疑与争论,一方面是因为观点不同,但更重要的还是希望企业能够结合自身实际有效选择最优性价比的质量工具,去掉浮华,让企业的质量管理落到实处。
02
SPC的由来
SPC控制图,又叫休哈特图,通过对生产过程的关键质量特性值进行测定、记录、评估并监测过程是否处于控制状态的一种图形方法。
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
休哈特将问题归结于变异中的普通原因和特殊原因。1924年的一天,休哈特把大家都熟悉的正态分布图旋转了90度(如下图),并以μ±3σ作为控制限,这就是控制图的原型。
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
最初的判异准则也只有一条,就是 看数据是否超出μ±3σ控制限 。
什么叫 判异 原则,就是判断有没有特殊原因的存在,也是SPC的核心之所在。
当发现有 特殊原因的存在 (通过控制图的异常,见本文 P5部分 ),就要找出原因是什么,并进行整改提升,如果产品特性比较多,需分别做控制图进行识别。
自控制图出现以后,变异分为普通原因和特殊原因。
普通原因 / Common Causes
一般认为是源自各种微小因素,对过程产生持续影响,结果稳定可预测,只能通过改变系统来减少普通原因,常需要管理层动作,如更新设备,还常包括:
—大量微小原因(如环境等)
—原材料在一定范围内的微小变异
—机械的微小振动
—仪器测量不十分精确
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
特殊原因 / Special Causes
一般认为 不是始终作用于过程的变差的原因,不符合统计学的分布, 当它们出现时将造成(整个)过程的分布改变,不需要改变系统就可以找出并解决特殊原因
实际的例子包括
—使用规格外的原材料
—设备坏了
—人员误操作
这个人为的划分被一直沿用至今。
当然,这些理论也收到了很多权威人士的质疑。
03
来自权威人士纷纷质疑
田口玄一
日本享誉全球的质量大师,创造了田口方法。
他曾说过“ 改进要有经济合理性,不能没完没了 ”。
Keki R. Bhote
哈佛大学博士,摩托罗拉质量和保证部总监。
直言不讳的说, 控制图“纯属浪费时间” 。
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
Banks David
美国统计局首席统计师,美国统计协会董事会成员。
他说,“ SPC大约是旧时代大学研究人员通过普通人难以理解晦涩公式来赢得名声的无用工具 。”
质量大师朱兰
朱兰说:“发明出控制图原型的 休哈特根本不懂工厂运营,完全没办法和操作工及管理人员进行有效的沟通 ”。
Bert Gunter
美国的著名统计顾问。曾说,“使用SPC的制造环境在快速变化,生产时间变得更短,数据产生的更多,质量要求更高和对计算能力要求更强大, 控制图这个古老的工具已经很难适应现代的生产和服务的需求 。 ”
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
Michel Baudin
40年实战经验的生产顾问。
说道: “ SPC是昨天的统计技术 ,用来解决昨天制造业的问题。它 没有能力解决今天的高科技问题 ,在成熟的行业它也变得完全没有必要。 它还没有完全消亡的原因是,它已经进入了客户强加给供应商的标准之中,虽然这些客户自己根本就不使用SPC 。这就是为什么你仍然可以看到有如此多的工厂走廊墙上贴着控制图。”
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
以上是近三十年里,国际上针对SPC公开发表不同声音的代表。
不过在国内,公开对SPC的抱怨几乎没有,私下的质疑倒是很多,我想这可能和中国人的中庸含蓄的性格有关系吧。
当然,也听到赞成 SPC的朋友说过:
你觉得SPC没用,是因为你没有真正理解SPC,或者你不会使用。
那上面那些质量大咖们呢?他们也不懂SPC,不懂统计学吗?
可能没那么简单!
04
日本使用SPC情况
江湖上经常听说这么个故事,战后的日本广泛推广和应用SPC,使日本的产品质量一举超越美国并处于世界领先地位,似乎日本在质量上的成功就是应用了SPC。
事实果真如此吗?
这里摘选部分文章的截图:
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
大意就是: 日本人追求效率,相比较那些复杂的工具, 在实际生产中,普遍使用的是相对简单易用的工具, 如柏拉图,直方图,散点图等,而不是依赖于SPC 。
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
质量当和效益挂钩时才有意义,而不是无条件实施不能带来经济收益的所谓改善。
05
SPC本身的缺陷
自相矛盾的逻辑
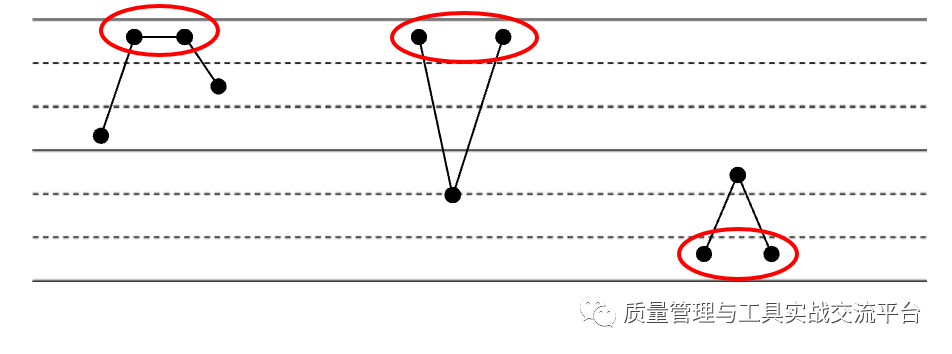
SPC的判异原则有很多,这里分享下常见的 八项判异准则:
a. 一个点远离中心线超过3个标准差
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
b. 连续7点位于中心线一侧
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
c. 连续6点上升或下降
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
d. 连续14点交替上下变化
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
e. 连续3点中有2点距中心线的距离超过2个标准差(同一侧)
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
f. 连续5点中有4点距中心线的距离超过1个标准差(同一侧)
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
g. 连续15个点排列在中心线1个标准差范围内(任一侧)
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
h. 连续8个点距中心线的距离大于1个标准差(任一侧)
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
为了简化,这里只讨论最初休哈特制定的 判异准则 ,是否超出3σ控制限。
如果数据点在3σ控制限以内,一般认为过程中的影响因素只有普通原因,不需改善。
如果 数据点 落在3σ控制限以外,则表明存在特殊原因,需采取措施进行改善。
因为按照休哈特理论,落在3σ以外的是小概率事件,要进行调查。不过,按照分布概率,落在3σ以外也可能是正常的分布。
设备是多种多样的,有的设备稳定性足够高,就像戴明的漏斗实验一样,不改变漏斗高度,小球落点的离散程度不会改变,小球出现在4σ(或者5σ)内也可能是普通原因。
但现在大多数的控制限是设置为3σ。
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
对于稳定性很好的设备,如果数据超过3σ控制限就报警,那么工厂花费了大量时间和资源记录跟踪数据,得到的却是大量的假报警,工程师为此要疲于奔命。
真正让生产员工迷惑的地方是,按照休哈特的理论,超出控制限有可能是普通原因也可能是特殊原因,让生产员工去调查,找到了就说是特殊原因,找不到,难道就是普通原因?
普通原因与特殊原因的划分
一般认为,特殊原因对过程影响较大或者特殊原因整改成本相对较低,但这都不是绝对的。但目前没有任何客观的真实数据来证实这一点, 实际上只是人为地把分析找到的原因归到特殊原因而已。
假设我们还是按照普通原因和特殊原因来划分, 在实际生产中,要获得更高的经济合理性,不一定是通过改进或消除特殊原因,更可以改进普通原因 。
从休哈特发明控制图100年来,社会化大生产已经发生了翻天覆地的变化,一台普通的设备通常是很多专业企业合作共同完成的。设备的精度和稳定程度在大踏步前进,留给客户操作人员改进的机会越来越少。
当你谷歌搜索到的所有SPC视频课程,你会发现绝大部分讲师在介绍用SPC查找特殊原因时, 给出的例子大都是换操作员工了,换原材料了,机器润滑不好了,螺丝松了,设备磨损了等等。
这些听起来更像是一些故事,而不是一些真实的案例。
当然,上面情况的发生的确会导致一些质量问题,也不是不重要,问题是企业有比SPC更加前置和高效的方法来预防这些问题,如,合格供应商名录,设备点检、维护和保养,员工上岗培训,分层审核,防呆等等。
普通原因和特殊原因, 本身没有天然的界限 。人为的分为两种原因,把简单的问题复杂化了,然后再按照所谓的分类去解决所谓的特殊原因。
戴明和AIAG制定的判异规则会增加误报率
在控制图中,如果7点(注:也有是6点之说)或更多的点连续上升或下降,人工判断或SPC软件将发出警报。现在已有多人要求取消戴明和AIAG制定的这个规则,因为这个规则在有些有意为之的过程里是无效的,虽然直觉上觉得合理,但结果只会大幅增加误报率。
06
SPC使用时的硬伤
除了上面说的自身缺陷之外,SPC在实际应用中也有一些硬伤。
公差限范围远大于控制限范围:
随着当代生产设备、检测设备以及工艺水平等方面的不断进步,制造型企业对产品质量特性的控制能力已经远远超出100年前的水平。客户要求供应商的过程能力CPK在1.67以上,甚至2已非罕见,那么就意味着质量水平相当于5σ-6σ。
人工判断或SPC软件报警,但产品是合格的, 这时控制图不仅没有好处,还帮倒忙。比如 世界著名500强公司 施耐德 ,在华工厂应用控制图监控生产过程中的若干关键质量特性,但该控制图中只有公差限,没有控制限。因为如果设置了控制限,那么系统会经常报警,使本就繁忙的工程师们疲于奔命 ,最终 索性取消控制限 。
公差限范围小于控制限范围:
通常理想状态,使用SPC时,要求过程稳定且CPK大于1。
项目在量产前策划阶段,对于具体的质量特性,企业工程技术人员通常预先评估采用哪种探测手段,并在过程开发时最终落实。比如可以用GO/NO GO检具100%检验或设计防错装置识别等,当然也可以使用控制图。
还有人会说,如果过程能力不足或者过程不稳定,通过控制图报警,这不是很好的机会改进产品质量吗?
未必,还要考虑实际经济效益。
举个例子, 我们都知道ENGEL,KM这些注塑机好,生产出来的产品可以 完全保证质量 ,但是价格太贵了。而一般品牌的注塑机呢?价格便宜很多,做出来的产品有一定比例的不合格,但是配备一个检验员就全部搞定了。
这就是让特殊原因存在的案例。
这里不是反对持续改进,持续改进是一个企业永恒的主题,但我们反对的是一谈到质量控制,言必称SPC。
公差限范围略大于控制限范围:
这时的CPK大于1,可能有人会说,这种情况下SPC控制图最有用,但其实给一线操作员工和质量人员带来的困扰同样也不少,为什么?
如果控制图报警,一线操作员工也不知道产品是否合格,有时还要在控制图的边上再做一个单值描点图(日本一些企业的作法)。
有些控制图上加上了公差限,的确是有所改善,但还是有问题,因为在控制图上显示的是X的平均值,当X平均值在公差限以内时,产品还是有可能不合格的。(当然,这时R图往往会报警,但操作员工还得另行计算一下,确认产品是否超差,因为控制限报警和产品不合格是两个严重度不一样的事情,对于一线工人来说,首要任务是产品合格然后才是持续改进。)
其它因素还有:
控制图需要持续不断地记录数据。一个控制图(均值极差控制图)只能监控一个质量特性,随着产品复杂度的增加以及供需链的不断变化,一个产品上会有多个关键质量特性。
一个工厂有上万个料号是非常普遍的现象 ,那么可以想象,使用控制图对这些产品的大量质量特性进行监控, 需要记录的数据以及需要付出的努力远远超出了企业所能承受的能力 。
如某公司一塑料产品有4个关键尺寸,该产品一共有2个模具,每个模具64穴,这些关键尺寸关系到客户产品的密封性能,塑料产品本身价值不高,但是一旦质量不合格,客户的损失将是非常巨大的。如果要取得客户订单,客户一定要求供应商签署质量连带责任协议。
如果使用控制图,每一次都要等到注塑机生产5个产品以后才能检验关键尺寸并记录,如果现场是纸质的控制图,操作工人还得计算这五个产品平均值和极差值,一个注塑工位就有4X64=258张控制图。两个模具,那么意味着要做2X4X64=512个控制图。如果这个公司有100个类似产品,那么意味着要有5万个控制图在生产现场。
每次注塑的时间间隔才几分钟,甚至有几十秒的,员工有时间记录吗?
用SPC软件能解决这些问题吗?
对于注塑产品,不仅要确保首件合格和末件合格,还要确保如何及时发现产品尺寸的变化,以便能及时清理冷却管路和维修模具,这对企业是一个极大的挑战。
如果您是这家企业的质量负责人,你会采用控制图来监控关键尺寸吗?您觉得控制图管的住质量吗?
再完美的设想,如果不能够满足实际生产现场的需求,那么也只能放在实验室里观赏。 不能够为实际生产服务,那么也就失去了它的价值。
07
谁在推行SPC
客户要求
由于SPC是汽车行业五大手册之一,虽然只是参考,但是很多汽车行业的客户和其它行业的部分客户在对其供应商实施质量评审和项目开发过程中,会把SPC作为一个条目来考核供应商。
为了提高通过第二方审核和第三方审核的概率,汽车行业供应商不得不在企业内推广SPC。
我们回放一下真实的质量评审场景:
供应商老老实实把所有的质量特性都列出来了,如果质量特性很多,除非供应商有大量的专业质量人员,否则不大可能都做到监控,即使有SPC软件系统也不可能(因为设置监控要花费大量的人力和时间,这个成本是很高的,不是每一个厂家都能负担得起的。)
如果评审员发现有的质量特性没有被监控,很可能给一个一般或严重不合格项。
而这很可能导致审核最终不通过。
即使质量特性都被监控了,评审员在现场评审时,如果发现了控制图报警,但是供应商没有及时给出分析和整改措施,这就要看评审员心情了,至少给一个观察项,给一个不合格项也很合理。
如果零部件供应商,负责客户审核的,你会怎么做?
多半会事先准备好一套美化过的SPC数据,等待评审员的到来,这样才能很有把握地保证质量评审顺利通过,企业不会因为质量评审出现问题而拿不到客户订单,导致管理层对质量部门不满意。
我们先不要站在道德的制高点上批评供应商的质量负责人,想一想,供应商质量负责人这么做是否也是一种无奈?
德国大陆 是一家非常知名的全球汽车零部件企业,其在华的一家工厂也遇到了SPC带来的烦恼。这家工厂每年要接待大量的客户二方年度审核、新项目审核和客户SQE定期检查及飞行检查,他们产品种类多,需要控制的质量特性也很多。
时不时,客户的质量人员就可能要求检查一下他们的产品控制图的填写情况,如果有异常报警,客户通常是一句话:你们要调查一下,写个整改报告。但供应商即使是编一个报告也要挺长时间,每天这么多的报警,如何应对?
编写假报告也要耗费大量的人力资源,不要忘记这一点。
后来这家工厂实在没办法, 干 脆招聘一个SPC数据“美化”技术员,每天专职美化数据 ,但数据也不是可以随随便便可以美化出来的,该工厂还用Excel编写个小程序,保证数据分布也是正态的,还能满足CPK的要求,极大提高了造假数据的效率,客户也很难再挑出毛病。
听起来可能像笑话?但是他们的质量人员根本乐不出来,他们有很大的挫败感,因为每天不得不做这些无聊没有意义的事情。
其实,这家大陆在华的工厂根本就没有用SPC来管控质量,但还不得不假装用SPC控制质量,并对客户宣称取得了很好的效果。
相对来说,国际大企业在理解SPC方面还是比一般企业要好,但他们为什么还要造假数据呢?
我本不想列出施耐德和大陆的名称,但我是想告诉大家,世界顶级的工业巨头尚且如此,您的企业实情如何?
尽管有许许多多的企业都在使用SPC,但情况不容乐观,理想很丰满,现实却如此骨感。
培训/咨询机构以及SPC工具厂商
首先,我们不否定有优秀的培训和咨询老师,不仅有专业水平,也从企业的实际角度看问题。
但是,也有一些例外:
有些是自己本身都没有理解和掌握SPC的原理,完全的照本宣科,自己都不知道自己说的是什么。
有些是书本主义,没有考虑到实际应用环境。
有些是揣着明白,装着糊涂。赚的盆满钵满与自砸饭碗之间,选择的是前者。不想说皇帝的新衣不好看,反正有人肯花钱,不拿白不拿。
更有甚者,牵强附会的应用。Q-DAS,为了增强SPC适用范围,把简单的事情搞得很复杂。刀具的寿命对某些企业是一个比较关键的数据,比如用刀具的磨损程度来预计刀具的寿命,按照刀具的磨损程度绘制出一个带有倾角上下控制限,通过与刀具报废线的交叉点来估算刀具寿命。
这个方法当然可以实现预测刀具寿命,但是对现场的操作工的理解上就不友好。简单的事情搞得那么复杂,用一个简单的描点图就可以实现的功能非得用繁琐的步骤实现。 似乎不复杂了体现不出自己水平似的。
质量管控的需求
自然还是有希望管理好企业的质量人在推广,希望能够帮助企业改善质量,这一点是不可否认的。
绝大部分管理措施出发点都是好的,但结果好不好就不一定了。
相比于其它质量工具, SPC耗费资源很多但产出却不高 。就像用长矛来捕鱼,的确能捕到鱼,观赏性非常好,可以用来炫耀手艺,但不完全适合当今的社会。
但是SPC一旦开启,就要针对每一个料号的每一个需要监控的质量特性持续不断收集数据,如果有电脑系统还好,没有电脑系统,还得用纸和Excel统计。
在企业竞争如此激烈的今天,还要让一线操作工人花费大量的时间记录这些SPC数据,当然企业还要投入培训SPC费用等,但这些费用仅仅是SPC相关费用的冰山一角。
很多人忽视的是质量工程师所耗费的心血和时间。
一个企业如果质量特性少还好,如果质量特性很多,新项目也很多。 质量工程师不得不花费大量的时间处理这些不确定的报警 ,这意味着很多其它事情被耽搁了。
08
企业怎么办?
现在有些人或企业认为质量管理就是SPC, 甚至有些MES系统开发商,直接把SPC当作质量管理模块卖给用户 ,不知道是自己不懂,还是有意为之。
汽车行业的用户也应该理性地去分辨,不应该被神话了的SPC所误导。工具应该为目的服务。
在此我们从两个方面给一些建议:
从质量管控工具有效性层面:
日本企业为了弥补SPC的不足而同时使用单点图,当然还有其它工具,比如合格率、ppm、缺陷统计等。配合柏拉图的使用,可以帮助企业快速锁定影响产品质量问题的“重要的少数”,起到事半功倍的效果,以及根据记录的数据进行相关性回归分析,帮助企业快速找到影响质量特性的因素,从而进行相关改进,进行质量预防,改善产品质量。
企业选择什么样的质量工具要根据自身的情况而定,不管黑猫白猫,抓住耗子的就是好猫。
客户和工厂需要的是合格的产品, SPC只是工具/手段,不要将手段当目的 。
从公司整体质量管理层面:
例子1 ,如果是一家生产纸箱,印刷品等技术含量不高的小企业,按照ISO9000的要求来做,就可能把企业管理的很不错。
例子2 ,如果一家电机厂有50条不同年代的产线,有2万种不同的物料,员工人数达到2000。企业发展到这个规模,可能以下问题是质量管理中的痛点:
什么原材料容易造成停工待料,都是什么问题?
那种类型电机合格率最低,都是什么问题?
给客户报价时,在那条产线生产,既能保证产品合格率又能保证成本可接受?
新产品开发时,类似的老产品都出现过什么问题?
这个规模的企业,质量体系早已经建立,质量特性数据也有一些,但是这些数据不是在纸质文档上就是在Excel中和其它系统中。这时企业可能需要一个能对多种物料,多条产线,多道工序,多个班组进行深度关联分析的系统以解决上述问题。
例子3 ,对于跨国采购公司和design house,有几十家甚至几百家供应商是很普遍的事,质量人员如何管理好供应商准时生产出合格产品很关键,否则就可能造成全球客户缺货或工厂停产。对供应商是否有能力生产出特定需求的产品要有把控能力,而不仅仅是根据质量评审的分数;开发新项目时对过往的历史数据和客户投诉了如指掌,并通过历史数据(包括客户投诉)有能力发现潜在的质量风险并在新项目开发时采取措施,;对出货检验要有大局观,既不能无原则放货,又不能把小问题无限放大不放货。如果该企业的产品种类高达上千种,供应商又分布在全国各地,但SQE人数却很少,这时的质量管理策略怎样制定才合理?
针对不同的公司规模、人员素质、不同的产品以及过程特性等,可以采用不同的质量管理工具进行管理。
合适的就是最好的,既要防患于未然又要因地制宜,不能是用工具找问题,而是应当根据问题找合适的工具。
09
怎么应付客户
前文做了很多论述,企业应该有自主权限根据实际情况来选择合适的质量工具。
但是对于SPC却很特殊,因为客户要求,不管效果如何,却不得不使用SPC。
这一点,在其他的四大工具中也存在, 客户要求大于一切,尤其在汽车行业 。
这的确是一个难题,这里也很难提供一个药到病除的解决方案。
供应商不可能冒着丢失订单的风险而违反客户的要求。
五大手册中的SPC,当年是主机厂为了在汽车供应链中推动持续改进,以客户为关注焦点,提高客户的满意度,要求供应商寻求一种更高效率的方式来提供产品和服务。
秉着这一宗旨,主机厂让组织的成员,不断尝试更高效的方法进行持续改善,可以采用不同的统计工具达到这一效果,并编制了五大工具之一的SPC手册。避免了当初无统一标准,各家各户要求各异,简化与减少了差异性。 但该手册也明确说明这是针对SPC的一个介绍。 企业根据客户要求的质量活动或者特性与客户沟通,可采用更有效的或者替代的方式。
解铃还须系铃人。 这里 也呼吁一下以汽车行业的质量人士,特别是主机厂的供应商管理团队。
主机厂要求的是合格的零部件,以及有效的公司管控方式,至于具体使用何种方式来管理质量,只要供应商能够证明有合适的工具进行管控,有稳定的提供合格产品并进行持续改善的能力,不是非得SPC这一条路。
少些形式主义,回归到事情的本质。
到这里,我们关于SPC的分享就结束了,各位朋友们,你们有因为“应审”而“造假”过吗?比如SPC的数据都是真实的吗?有时候,可能还不是一个人造假吧,是搞质量的,做体系带领大家一起造假吧!
今天分享的是SPC。这两年很热的FMEA(潜在失效模式及后果分析)呢?
其原理,其本质,简单到令人发指!是谁把他搞复杂了的?
MSA呢,APQP和PPAP呢?
五大工具在国外也像在中国那么流行吗?还是只是一帮人、一些机构在忽悠中国企业?
最后,再多问一句:五大工具对你们公司真的有用吗?
收起阅读 »
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
你的感受如何?
当你知道这句话是总经理对刚入职的体系经理说的,感受又如何?
搞质量体系的,自然也离不开质量工具,说到质量工具的绕不开的当然是五大工具。
五大工具太有名了。有名到如果你不知道它们,都不好意思说自己是在汽车行业混的。虽说不是强制性要求,可并不妨碍各大主机厂对它们的推崇,进行影响着整个汽车行业。
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
它们分别是:
APQP 产品质量先期策划 Advanced Product Quality Planning
FMEA 潜在失效模式及后果分析 Failure Mode & Effect Analyse
MSA 测量系统分析 Measurement System Analyse
SPC 统计过程控制 Statistical Process Control
PPAP 生产件批准程序 Production Part Approval Process
这五大手册源自于美国QS9000质量体系,是三大汽车公司克来斯勒、福特和通用制定的对其供方的标准质量要求。
不过,名气大了,就显得有些“高冷”,很多朋友在学习五大手册的时候总觉得有些高深难懂。 甚至有人说 五大工具只会忽悠中国人,公司里 搞体系的在带头造假!
是这个情况吗?
今天应审指挥部分享一篇关于五大工具中SPC的 深度解读文章 。
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
当然,这里还是要简单介绍一下,S PC 统计过程控制 的研究对象其实只有一个,就是过程!
通过统计分析技术对生产过程(注意MSA的对象是测量系统)进行实时监控,科学的区分出生产过程中产品质量的随机波动与异常波动,从而对生产过程的异常趋势提出预警,以便生产管理人员及时采取措施,消除异常,恢复过程的稳定,从而达到提高和控制质量的目的。
简单说来,SPC的通过控制好各种过程(核心是生产过程),最终生产出来的产品质量稳定。 文章有点长,不过满满干货,性价比绝对杠杠的,一起来看看吧。
01
前言
1924年,休哈特带着他的控制图“问世”之后,被以汽车行业为代表的制造业,广泛用来监控和改进生产过程,试图通过产品质量特性变化趋势来进行质量预防,改变旧有的事后质量检验的方式,来降低质量成本,并被列入汽车行业质量管理五大工具之一。
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
其实,在以美国为代表的制造业强国中,不论是统计专家还是质量专家,针对SPC的实用性以及有效性的思考和质疑之声,从来就没停止过。
日本更是以实际效用为准绳,而不是在实际推广中原封不动地照搬照抄SPC。
对于SPC的质疑与争论,一方面是因为观点不同,但更重要的还是希望企业能够结合自身实际有效选择最优性价比的质量工具,去掉浮华,让企业的质量管理落到实处。
02
SPC的由来
SPC控制图,又叫休哈特图,通过对生产过程的关键质量特性值进行测定、记录、评估并监测过程是否处于控制状态的一种图形方法。
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
休哈特将问题归结于变异中的普通原因和特殊原因。1924年的一天,休哈特把大家都熟悉的正态分布图旋转了90度(如下图),并以μ±3σ作为控制限,这就是控制图的原型。
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
最初的判异准则也只有一条,就是 看数据是否超出μ±3σ控制限 。
什么叫 判异 原则,就是判断有没有特殊原因的存在,也是SPC的核心之所在。
当发现有 特殊原因的存在 (通过控制图的异常,见本文 P5部分 ),就要找出原因是什么,并进行整改提升,如果产品特性比较多,需分别做控制图进行识别。
自控制图出现以后,变异分为普通原因和特殊原因。
普通原因 / Common Causes
一般认为是源自各种微小因素,对过程产生持续影响,结果稳定可预测,只能通过改变系统来减少普通原因,常需要管理层动作,如更新设备,还常包括:
—大量微小原因(如环境等)
—原材料在一定范围内的微小变异
—机械的微小振动
—仪器测量不十分精确
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
特殊原因 / Special Causes
一般认为 不是始终作用于过程的变差的原因,不符合统计学的分布, 当它们出现时将造成(整个)过程的分布改变,不需要改变系统就可以找出并解决特殊原因
实际的例子包括
—使用规格外的原材料
—设备坏了
—人员误操作
这个人为的划分被一直沿用至今。
当然,这些理论也收到了很多权威人士的质疑。
03
来自权威人士纷纷质疑
田口玄一
日本享誉全球的质量大师,创造了田口方法。
他曾说过“ 改进要有经济合理性,不能没完没了 ”。
Keki R. Bhote
哈佛大学博士,摩托罗拉质量和保证部总监。
直言不讳的说, 控制图“纯属浪费时间” 。
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
Banks David
美国统计局首席统计师,美国统计协会董事会成员。
他说,“ SPC大约是旧时代大学研究人员通过普通人难以理解晦涩公式来赢得名声的无用工具 。”
质量大师朱兰
朱兰说:“发明出控制图原型的 休哈特根本不懂工厂运营,完全没办法和操作工及管理人员进行有效的沟通 ”。
Bert Gunter
美国的著名统计顾问。曾说,“使用SPC的制造环境在快速变化,生产时间变得更短,数据产生的更多,质量要求更高和对计算能力要求更强大, 控制图这个古老的工具已经很难适应现代的生产和服务的需求 。 ”
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
Michel Baudin
40年实战经验的生产顾问。
说道: “ SPC是昨天的统计技术 ,用来解决昨天制造业的问题。它 没有能力解决今天的高科技问题 ,在成熟的行业它也变得完全没有必要。 它还没有完全消亡的原因是,它已经进入了客户强加给供应商的标准之中,虽然这些客户自己根本就不使用SPC 。这就是为什么你仍然可以看到有如此多的工厂走廊墙上贴着控制图。”
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
以上是近三十年里,国际上针对SPC公开发表不同声音的代表。
不过在国内,公开对SPC的抱怨几乎没有,私下的质疑倒是很多,我想这可能和中国人的中庸含蓄的性格有关系吧。
当然,也听到赞成 SPC的朋友说过:
你觉得SPC没用,是因为你没有真正理解SPC,或者你不会使用。
那上面那些质量大咖们呢?他们也不懂SPC,不懂统计学吗?
可能没那么简单!
04
日本使用SPC情况
江湖上经常听说这么个故事,战后的日本广泛推广和应用SPC,使日本的产品质量一举超越美国并处于世界领先地位,似乎日本在质量上的成功就是应用了SPC。
事实果真如此吗?
这里摘选部分文章的截图:
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
大意就是: 日本人追求效率,相比较那些复杂的工具, 在实际生产中,普遍使用的是相对简单易用的工具, 如柏拉图,直方图,散点图等,而不是依赖于SPC 。
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
质量当和效益挂钩时才有意义,而不是无条件实施不能带来经济收益的所谓改善。
05
SPC本身的缺陷
自相矛盾的逻辑
SPC的判异原则有很多,这里分享下常见的 八项判异准则:
a. 一个点远离中心线超过3个标准差
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
b. 连续7点位于中心线一侧
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
c. 连续6点上升或下降
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
d. 连续14点交替上下变化
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
e. 连续3点中有2点距中心线的距离超过2个标准差(同一侧)
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
f. 连续5点中有4点距中心线的距离超过1个标准差(同一侧)
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
g. 连续15个点排列在中心线1个标准差范围内(任一侧)
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
h. 连续8个点距中心线的距离大于1个标准差(任一侧)
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
为了简化,这里只讨论最初休哈特制定的 判异准则 ,是否超出3σ控制限。
如果数据点在3σ控制限以内,一般认为过程中的影响因素只有普通原因,不需改善。
如果 数据点 落在3σ控制限以外,则表明存在特殊原因,需采取措施进行改善。
因为按照休哈特理论,落在3σ以外的是小概率事件,要进行调查。不过,按照分布概率,落在3σ以外也可能是正常的分布。
设备是多种多样的,有的设备稳定性足够高,就像戴明的漏斗实验一样,不改变漏斗高度,小球落点的离散程度不会改变,小球出现在4σ(或者5σ)内也可能是普通原因。
但现在大多数的控制限是设置为3σ。
[新知达人, 不会作假就搞不了质量体系,五大工具只忽悠中国人?]
对于稳定性很好的设备,如果数据超过3σ控制限就报警,那么工厂花费了大量时间和资源记录跟踪数据,得到的却是大量的假报警,工程师为此要疲于奔命。
真正让生产员工迷惑的地方是,按照休哈特的理论,超出控制限有可能是普通原因也可能是特殊原因,让生产员工去调查,找到了就说是特殊原因,找不到,难道就是普通原因?
普通原因与特殊原因的划分
一般认为,特殊原因对过程影响较大或者特殊原因整改成本相对较低,但这都不是绝对的。但目前没有任何客观的真实数据来证实这一点, 实际上只是人为地把分析找到的原因归到特殊原因而已。
假设我们还是按照普通原因和特殊原因来划分, 在实际生产中,要获得更高的经济合理性,不一定是通过改进或消除特殊原因,更可以改进普通原因 。
从休哈特发明控制图100年来,社会化大生产已经发生了翻天覆地的变化,一台普通的设备通常是很多专业企业合作共同完成的。设备的精度和稳定程度在大踏步前进,留给客户操作人员改进的机会越来越少。
当你谷歌搜索到的所有SPC视频课程,你会发现绝大部分讲师在介绍用SPC查找特殊原因时, 给出的例子大都是换操作员工了,换原材料了,机器润滑不好了,螺丝松了,设备磨损了等等。
这些听起来更像是一些故事,而不是一些真实的案例。
当然,上面情况的发生的确会导致一些质量问题,也不是不重要,问题是企业有比SPC更加前置和高效的方法来预防这些问题,如,合格供应商名录,设备点检、维护和保养,员工上岗培训,分层审核,防呆等等。
普通原因和特殊原因, 本身没有天然的界限 。人为的分为两种原因,把简单的问题复杂化了,然后再按照所谓的分类去解决所谓的特殊原因。
戴明和AIAG制定的判异规则会增加误报率
在控制图中,如果7点(注:也有是6点之说)或更多的点连续上升或下降,人工判断或SPC软件将发出警报。现在已有多人要求取消戴明和AIAG制定的这个规则,因为这个规则在有些有意为之的过程里是无效的,虽然直觉上觉得合理,但结果只会大幅增加误报率。
06
SPC使用时的硬伤
除了上面说的自身缺陷之外,SPC在实际应用中也有一些硬伤。
公差限范围远大于控制限范围:
随着当代生产设备、检测设备以及工艺水平等方面的不断进步,制造型企业对产品质量特性的控制能力已经远远超出100年前的水平。客户要求供应商的过程能力CPK在1.67以上,甚至2已非罕见,那么就意味着质量水平相当于5σ-6σ。
人工判断或SPC软件报警,但产品是合格的, 这时控制图不仅没有好处,还帮倒忙。比如 世界著名500强公司 施耐德 ,在华工厂应用控制图监控生产过程中的若干关键质量特性,但该控制图中只有公差限,没有控制限。因为如果设置了控制限,那么系统会经常报警,使本就繁忙的工程师们疲于奔命 ,最终 索性取消控制限 。
公差限范围小于控制限范围:
通常理想状态,使用SPC时,要求过程稳定且CPK大于1。
项目在量产前策划阶段,对于具体的质量特性,企业工程技术人员通常预先评估采用哪种探测手段,并在过程开发时最终落实。比如可以用GO/NO GO检具100%检验或设计防错装置识别等,当然也可以使用控制图。
还有人会说,如果过程能力不足或者过程不稳定,通过控制图报警,这不是很好的机会改进产品质量吗?
未必,还要考虑实际经济效益。
举个例子, 我们都知道ENGEL,KM这些注塑机好,生产出来的产品可以 完全保证质量 ,但是价格太贵了。而一般品牌的注塑机呢?价格便宜很多,做出来的产品有一定比例的不合格,但是配备一个检验员就全部搞定了。
这就是让特殊原因存在的案例。
这里不是反对持续改进,持续改进是一个企业永恒的主题,但我们反对的是一谈到质量控制,言必称SPC。
公差限范围略大于控制限范围:
这时的CPK大于1,可能有人会说,这种情况下SPC控制图最有用,但其实给一线操作员工和质量人员带来的困扰同样也不少,为什么?
如果控制图报警,一线操作员工也不知道产品是否合格,有时还要在控制图的边上再做一个单值描点图(日本一些企业的作法)。
有些控制图上加上了公差限,的确是有所改善,但还是有问题,因为在控制图上显示的是X的平均值,当X平均值在公差限以内时,产品还是有可能不合格的。(当然,这时R图往往会报警,但操作员工还得另行计算一下,确认产品是否超差,因为控制限报警和产品不合格是两个严重度不一样的事情,对于一线工人来说,首要任务是产品合格然后才是持续改进。)
其它因素还有:
控制图需要持续不断地记录数据。一个控制图(均值极差控制图)只能监控一个质量特性,随着产品复杂度的增加以及供需链的不断变化,一个产品上会有多个关键质量特性。
一个工厂有上万个料号是非常普遍的现象 ,那么可以想象,使用控制图对这些产品的大量质量特性进行监控, 需要记录的数据以及需要付出的努力远远超出了企业所能承受的能力 。
如某公司一塑料产品有4个关键尺寸,该产品一共有2个模具,每个模具64穴,这些关键尺寸关系到客户产品的密封性能,塑料产品本身价值不高,但是一旦质量不合格,客户的损失将是非常巨大的。如果要取得客户订单,客户一定要求供应商签署质量连带责任协议。
如果使用控制图,每一次都要等到注塑机生产5个产品以后才能检验关键尺寸并记录,如果现场是纸质的控制图,操作工人还得计算这五个产品平均值和极差值,一个注塑工位就有4X64=258张控制图。两个模具,那么意味着要做2X4X64=512个控制图。如果这个公司有100个类似产品,那么意味着要有5万个控制图在生产现场。
每次注塑的时间间隔才几分钟,甚至有几十秒的,员工有时间记录吗?
用SPC软件能解决这些问题吗?
对于注塑产品,不仅要确保首件合格和末件合格,还要确保如何及时发现产品尺寸的变化,以便能及时清理冷却管路和维修模具,这对企业是一个极大的挑战。
如果您是这家企业的质量负责人,你会采用控制图来监控关键尺寸吗?您觉得控制图管的住质量吗?
再完美的设想,如果不能够满足实际生产现场的需求,那么也只能放在实验室里观赏。 不能够为实际生产服务,那么也就失去了它的价值。
07
谁在推行SPC
客户要求
由于SPC是汽车行业五大手册之一,虽然只是参考,但是很多汽车行业的客户和其它行业的部分客户在对其供应商实施质量评审和项目开发过程中,会把SPC作为一个条目来考核供应商。
为了提高通过第二方审核和第三方审核的概率,汽车行业供应商不得不在企业内推广SPC。
我们回放一下真实的质量评审场景:
供应商老老实实把所有的质量特性都列出来了,如果质量特性很多,除非供应商有大量的专业质量人员,否则不大可能都做到监控,即使有SPC软件系统也不可能(因为设置监控要花费大量的人力和时间,这个成本是很高的,不是每一个厂家都能负担得起的。)
如果评审员发现有的质量特性没有被监控,很可能给一个一般或严重不合格项。
而这很可能导致审核最终不通过。
即使质量特性都被监控了,评审员在现场评审时,如果发现了控制图报警,但是供应商没有及时给出分析和整改措施,这就要看评审员心情了,至少给一个观察项,给一个不合格项也很合理。
如果零部件供应商,负责客户审核的,你会怎么做?
多半会事先准备好一套美化过的SPC数据,等待评审员的到来,这样才能很有把握地保证质量评审顺利通过,企业不会因为质量评审出现问题而拿不到客户订单,导致管理层对质量部门不满意。
我们先不要站在道德的制高点上批评供应商的质量负责人,想一想,供应商质量负责人这么做是否也是一种无奈?
德国大陆 是一家非常知名的全球汽车零部件企业,其在华的一家工厂也遇到了SPC带来的烦恼。这家工厂每年要接待大量的客户二方年度审核、新项目审核和客户SQE定期检查及飞行检查,他们产品种类多,需要控制的质量特性也很多。
时不时,客户的质量人员就可能要求检查一下他们的产品控制图的填写情况,如果有异常报警,客户通常是一句话:你们要调查一下,写个整改报告。但供应商即使是编一个报告也要挺长时间,每天这么多的报警,如何应对?
编写假报告也要耗费大量的人力资源,不要忘记这一点。
后来这家工厂实在没办法, 干 脆招聘一个SPC数据“美化”技术员,每天专职美化数据 ,但数据也不是可以随随便便可以美化出来的,该工厂还用Excel编写个小程序,保证数据分布也是正态的,还能满足CPK的要求,极大提高了造假数据的效率,客户也很难再挑出毛病。
听起来可能像笑话?但是他们的质量人员根本乐不出来,他们有很大的挫败感,因为每天不得不做这些无聊没有意义的事情。
其实,这家大陆在华的工厂根本就没有用SPC来管控质量,但还不得不假装用SPC控制质量,并对客户宣称取得了很好的效果。
相对来说,国际大企业在理解SPC方面还是比一般企业要好,但他们为什么还要造假数据呢?
我本不想列出施耐德和大陆的名称,但我是想告诉大家,世界顶级的工业巨头尚且如此,您的企业实情如何?
尽管有许许多多的企业都在使用SPC,但情况不容乐观,理想很丰满,现实却如此骨感。
培训/咨询机构以及SPC工具厂商
首先,我们不否定有优秀的培训和咨询老师,不仅有专业水平,也从企业的实际角度看问题。
但是,也有一些例外:
有些是自己本身都没有理解和掌握SPC的原理,完全的照本宣科,自己都不知道自己说的是什么。
有些是书本主义,没有考虑到实际应用环境。
有些是揣着明白,装着糊涂。赚的盆满钵满与自砸饭碗之间,选择的是前者。不想说皇帝的新衣不好看,反正有人肯花钱,不拿白不拿。
更有甚者,牵强附会的应用。Q-DAS,为了增强SPC适用范围,把简单的事情搞得很复杂。刀具的寿命对某些企业是一个比较关键的数据,比如用刀具的磨损程度来预计刀具的寿命,按照刀具的磨损程度绘制出一个带有倾角上下控制限,通过与刀具报废线的交叉点来估算刀具寿命。
这个方法当然可以实现预测刀具寿命,但是对现场的操作工的理解上就不友好。简单的事情搞得那么复杂,用一个简单的描点图就可以实现的功能非得用繁琐的步骤实现。 似乎不复杂了体现不出自己水平似的。
质量管控的需求
自然还是有希望管理好企业的质量人在推广,希望能够帮助企业改善质量,这一点是不可否认的。
绝大部分管理措施出发点都是好的,但结果好不好就不一定了。
相比于其它质量工具, SPC耗费资源很多但产出却不高 。就像用长矛来捕鱼,的确能捕到鱼,观赏性非常好,可以用来炫耀手艺,但不完全适合当今的社会。
但是SPC一旦开启,就要针对每一个料号的每一个需要监控的质量特性持续不断收集数据,如果有电脑系统还好,没有电脑系统,还得用纸和Excel统计。
在企业竞争如此激烈的今天,还要让一线操作工人花费大量的时间记录这些SPC数据,当然企业还要投入培训SPC费用等,但这些费用仅仅是SPC相关费用的冰山一角。
很多人忽视的是质量工程师所耗费的心血和时间。
一个企业如果质量特性少还好,如果质量特性很多,新项目也很多。 质量工程师不得不花费大量的时间处理这些不确定的报警 ,这意味着很多其它事情被耽搁了。
08
企业怎么办?
现在有些人或企业认为质量管理就是SPC, 甚至有些MES系统开发商,直接把SPC当作质量管理模块卖给用户 ,不知道是自己不懂,还是有意为之。
汽车行业的用户也应该理性地去分辨,不应该被神话了的SPC所误导。工具应该为目的服务。
在此我们从两个方面给一些建议:
从质量管控工具有效性层面:
日本企业为了弥补SPC的不足而同时使用单点图,当然还有其它工具,比如合格率、ppm、缺陷统计等。配合柏拉图的使用,可以帮助企业快速锁定影响产品质量问题的“重要的少数”,起到事半功倍的效果,以及根据记录的数据进行相关性回归分析,帮助企业快速找到影响质量特性的因素,从而进行相关改进,进行质量预防,改善产品质量。
企业选择什么样的质量工具要根据自身的情况而定,不管黑猫白猫,抓住耗子的就是好猫。
客户和工厂需要的是合格的产品, SPC只是工具/手段,不要将手段当目的 。
从公司整体质量管理层面:
例子1 ,如果是一家生产纸箱,印刷品等技术含量不高的小企业,按照ISO9000的要求来做,就可能把企业管理的很不错。
例子2 ,如果一家电机厂有50条不同年代的产线,有2万种不同的物料,员工人数达到2000。企业发展到这个规模,可能以下问题是质量管理中的痛点:
什么原材料容易造成停工待料,都是什么问题?
那种类型电机合格率最低,都是什么问题?
给客户报价时,在那条产线生产,既能保证产品合格率又能保证成本可接受?
新产品开发时,类似的老产品都出现过什么问题?
这个规模的企业,质量体系早已经建立,质量特性数据也有一些,但是这些数据不是在纸质文档上就是在Excel中和其它系统中。这时企业可能需要一个能对多种物料,多条产线,多道工序,多个班组进行深度关联分析的系统以解决上述问题。
例子3 ,对于跨国采购公司和design house,有几十家甚至几百家供应商是很普遍的事,质量人员如何管理好供应商准时生产出合格产品很关键,否则就可能造成全球客户缺货或工厂停产。对供应商是否有能力生产出特定需求的产品要有把控能力,而不仅仅是根据质量评审的分数;开发新项目时对过往的历史数据和客户投诉了如指掌,并通过历史数据(包括客户投诉)有能力发现潜在的质量风险并在新项目开发时采取措施,;对出货检验要有大局观,既不能无原则放货,又不能把小问题无限放大不放货。如果该企业的产品种类高达上千种,供应商又分布在全国各地,但SQE人数却很少,这时的质量管理策略怎样制定才合理?
针对不同的公司规模、人员素质、不同的产品以及过程特性等,可以采用不同的质量管理工具进行管理。
合适的就是最好的,既要防患于未然又要因地制宜,不能是用工具找问题,而是应当根据问题找合适的工具。
09
怎么应付客户
前文做了很多论述,企业应该有自主权限根据实际情况来选择合适的质量工具。
但是对于SPC却很特殊,因为客户要求,不管效果如何,却不得不使用SPC。
这一点,在其他的四大工具中也存在, 客户要求大于一切,尤其在汽车行业 。
这的确是一个难题,这里也很难提供一个药到病除的解决方案。
供应商不可能冒着丢失订单的风险而违反客户的要求。
五大手册中的SPC,当年是主机厂为了在汽车供应链中推动持续改进,以客户为关注焦点,提高客户的满意度,要求供应商寻求一种更高效率的方式来提供产品和服务。
秉着这一宗旨,主机厂让组织的成员,不断尝试更高效的方法进行持续改善,可以采用不同的统计工具达到这一效果,并编制了五大工具之一的SPC手册。避免了当初无统一标准,各家各户要求各异,简化与减少了差异性。 但该手册也明确说明这是针对SPC的一个介绍。 企业根据客户要求的质量活动或者特性与客户沟通,可采用更有效的或者替代的方式。
解铃还须系铃人。 这里 也呼吁一下以汽车行业的质量人士,特别是主机厂的供应商管理团队。
主机厂要求的是合格的零部件,以及有效的公司管控方式,至于具体使用何种方式来管理质量,只要供应商能够证明有合适的工具进行管控,有稳定的提供合格产品并进行持续改善的能力,不是非得SPC这一条路。
少些形式主义,回归到事情的本质。
到这里,我们关于SPC的分享就结束了,各位朋友们,你们有因为“应审”而“造假”过吗?比如SPC的数据都是真实的吗?有时候,可能还不是一个人造假吧,是搞质量的,做体系带领大家一起造假吧!
今天分享的是SPC。这两年很热的FMEA(潜在失效模式及后果分析)呢?
其原理,其本质,简单到令人发指!是谁把他搞复杂了的?
MSA呢,APQP和PPAP呢?
五大工具在国外也像在中国那么流行吗?还是只是一帮人、一些机构在忽悠中国企业?
最后,再多问一句:五大工具对你们公司真的有用吗?
收起阅读 »
控制图为什么能够发现失控?
假设你是一位质量工程师,在使用SPC控制图控制你们的生产过程。某一天,当你发现控制图失控的时候,你要求停线调查原因、隔离产品,那么你很可能将遭受到来自生产部门和销售部门的质疑和压力:你凭什么让我们停线?你凭什么不让我们交付?你凭什么说超过了那两条控制限过程就有问题?
这时你就需要拿出你掌握的底层逻辑,即控制图的理论依据来了,否则,就不能说服他们。
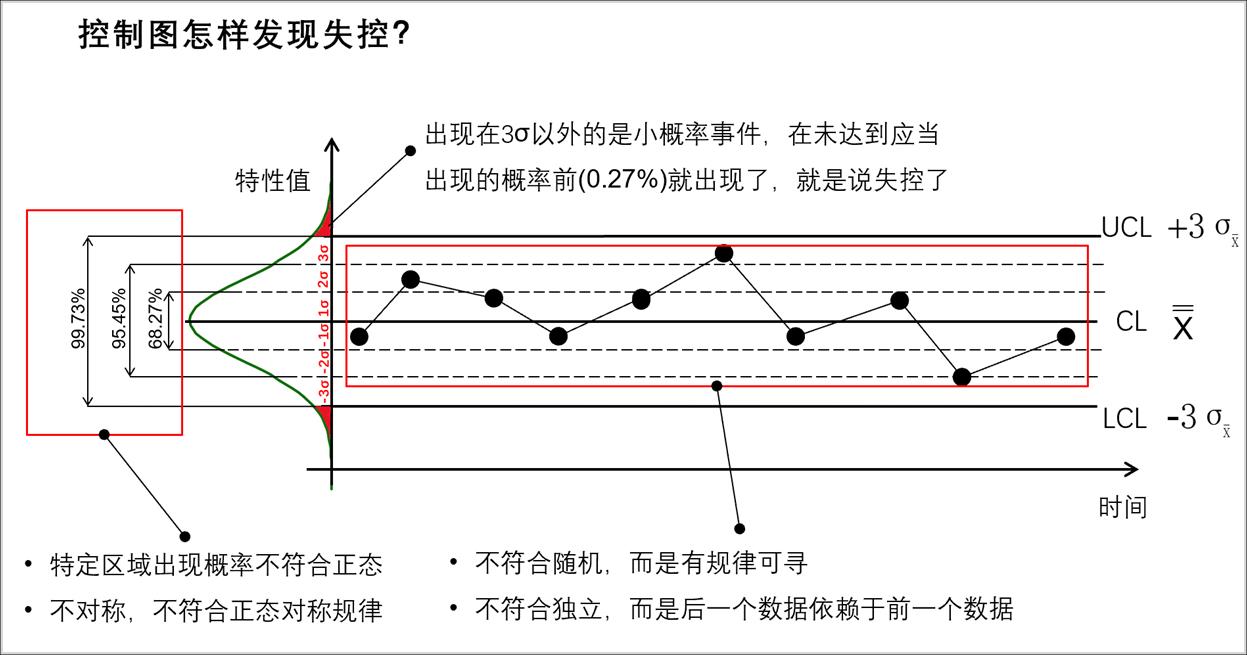
我们先来看一下控制图的第一条判异准则:当有一点超过中心线上、下3个标准差的控制限。
在绝大多数制造过程中,如果特性值的影响因素有若干,且没有一个是起主导作用的,这些特性数据就会符合或者大致符合正态分布,这是一个经过大量实践证明了的客观规律,如下图所示,它是一个概率分布图。正态分布中,位于均值μ两侧各3个σ以外的概率为(1-99.73%)=0.27%。
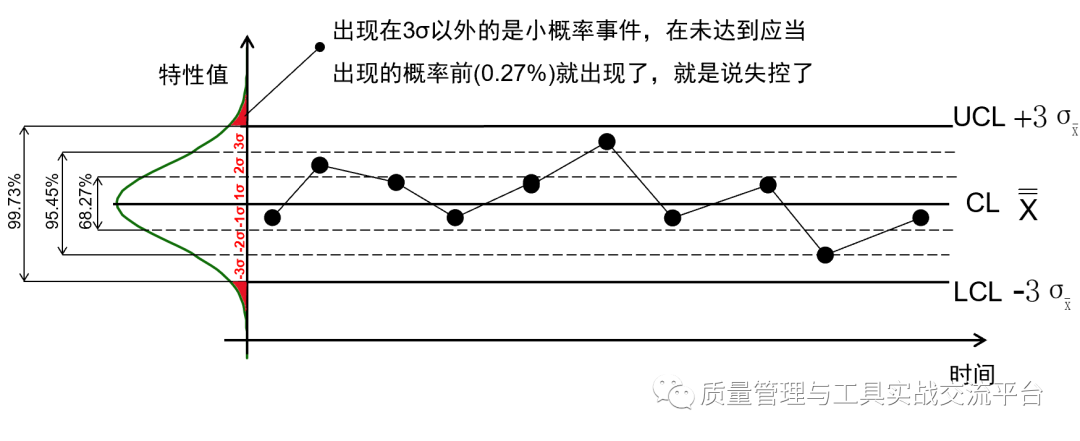
在常规控制图的均值-极差控制图中,以中心线上、下3倍子组均值标准差为均值图的上、下控制限,如下图所示。均值图中的点代表子组的均值,根据中心极限定理,它们之间也符合正态分布,而且会比单值更加符合。根据正态分布的规律可知,在过程稳定受控(也叫统计受控)的状态下,出现一个数据点超过控制限的概率仅为0.27%,反之,如果出现的概率超过0.27%,则说明该生产过程不稳定,即失控。
换种说法就是,如果过程稳定受控,平均1/0.0027≈370个点中才有一个点超出控制限,这是一个妥妥的小概率事件!小概率事件的发生概率很小,它在一次试验中是几乎不可能发生的,但在多次重复试验中是必然发生的,在这里的“多次”,就是370次以上。那么,一旦我们真的发现有点超过了控制限,首先应当问:上次有点超过控制限到这一次,是经历了多久?如果两次相隔达不到370个点以上,那么就说明过程已经失控了。
在未达到小概率事件出现的机会之前就出现了,说明过程原来的稳定状态已经被一种起主导作用的原因破坏了,这个原因叫做特殊原因,我们应当停下生产线来找到这个原因,否则就会出现批量的不良品。
我们近些年中每年动不动就会遭遇百年不遇的暴雨、洪灾、干旱,而百年不遇本来就是一个小概率,为什么近几年每年都会发生呢?这是因为存在了特殊原因,使得我们这个星球上的大气系统变得不再稳定,这个特殊原因就是气候变暖!类似的社会生活中的例子可以举出很多。
我们再看一下准则5:连续3个点中,有2个位于中心线同侧2倍标准差以外。
按照正态分布的概率密度分布规律,一个点出现在中心线一侧2标准差以外的概率为:P(X>μ+2σ)=1-P(X≤μ+2σ)=1-0.9772=0.0228,P(X<μ-2σ)=0.0228,则连续3个点中有2个点位于中心线同侧2标准差以外的概率应:
这更是一个小概率事件!
总之,在常规控制图中,我们基于大多数稳定的制造过程数据符合或接近正态分布这一客观规律,做一个过程稳定的假设,即过程数据符合正态分布,一旦出现不符合正态分布的情况,我们就判定这个过程失控了,就必须停止生产,找出导致失控的特殊原因。
这就是为什么控制图能够发现失控的底层逻辑,即它的理论基础。 收起阅读 »
这时你就需要拿出你掌握的底层逻辑,即控制图的理论依据来了,否则,就不能说服他们。
我们先来看一下控制图的第一条判异准则:当有一点超过中心线上、下3个标准差的控制限。
在绝大多数制造过程中,如果特性值的影响因素有若干,且没有一个是起主导作用的,这些特性数据就会符合或者大致符合正态分布,这是一个经过大量实践证明了的客观规律,如下图所示,它是一个概率分布图。正态分布中,位于均值μ两侧各3个σ以外的概率为(1-99.73%)=0.27%。
在常规控制图的均值-极差控制图中,以中心线上、下3倍子组均值标准差为均值图的上、下控制限,如下图所示。均值图中的点代表子组的均值,根据中心极限定理,它们之间也符合正态分布,而且会比单值更加符合。根据正态分布的规律可知,在过程稳定受控(也叫统计受控)的状态下,出现一个数据点超过控制限的概率仅为0.27%,反之,如果出现的概率超过0.27%,则说明该生产过程不稳定,即失控。
换种说法就是,如果过程稳定受控,平均1/0.0027≈370个点中才有一个点超出控制限,这是一个妥妥的小概率事件!小概率事件的发生概率很小,它在一次试验中是几乎不可能发生的,但在多次重复试验中是必然发生的,在这里的“多次”,就是370次以上。那么,一旦我们真的发现有点超过了控制限,首先应当问:上次有点超过控制限到这一次,是经历了多久?如果两次相隔达不到370个点以上,那么就说明过程已经失控了。
在未达到小概率事件出现的机会之前就出现了,说明过程原来的稳定状态已经被一种起主导作用的原因破坏了,这个原因叫做特殊原因,我们应当停下生产线来找到这个原因,否则就会出现批量的不良品。
我们近些年中每年动不动就会遭遇百年不遇的暴雨、洪灾、干旱,而百年不遇本来就是一个小概率,为什么近几年每年都会发生呢?这是因为存在了特殊原因,使得我们这个星球上的大气系统变得不再稳定,这个特殊原因就是气候变暖!类似的社会生活中的例子可以举出很多。
我们再看一下准则5:连续3个点中,有2个位于中心线同侧2倍标准差以外。
按照正态分布的概率密度分布规律,一个点出现在中心线一侧2标准差以外的概率为:P(X>μ+2σ)=1-P(X≤μ+2σ)=1-0.9772=0.0228,P(X<μ-2σ)=0.0228,则连续3个点中有2个点位于中心线同侧2标准差以外的概率应:
这更是一个小概率事件!
总之,在常规控制图中,我们基于大多数稳定的制造过程数据符合或接近正态分布这一客观规律,做一个过程稳定的假设,即过程数据符合正态分布,一旦出现不符合正态分布的情况,我们就判定这个过程失控了,就必须停止生产,找出导致失控的特殊原因。
这就是为什么控制图能够发现失控的底层逻辑,即它的理论基础。 收起阅读 »
一个均值-极差控图子组大小的问题
这是一个来自6SQ品质论坛的问题,原问题是:当每个子组内包含2个样本,共40个子组时,均值控制图上只有一个点超出控制限;当每个子组内包含3个样本,共27个子组时,均值控制图上反而有4个点超出控制限。这是为什么?
下面是我的回答,并在此基础上展开说明如何确定子组的大小。
这是SPC控制图的一个最基本的概念之一。在均值-极差图中,子组越大,则均值上下控制限之间越窄,也就是说,均值控制图越灵敏。这是因为,均值图的控制限公式为:总均值加/减3倍的均值标准差,即:
根据中心极限定理,均值标准差等于单值的标准差除以子组大小n的平方根,
也就是说,子组越大,则均值的标准差就越小,由此计算出来的均值上下限间就越窄。因此,每个子组抽样越多,即子组越大,则均值图上超出控制限的点会越多。
如果使用平均极差来计算控制限,我们可以发现A2这个系数也会随着子组大小的增加而减小。
子组的极差的大小,从理论上来讲,会随着子组大小的增加而增加,但是当子组中样本的数量大于9后,用极差来估计过程标准差时就不准确了,应当使用子组的标准差S来估计了。下图列出了不同子组大小之下,用子组的平均极差和平均标准差来估计过程标准差时的差异。
而当子组在9以下时,极差随子组大小的变化并没有那么明显,特别是当过程处于稳定的状态时候。
由此可见,控制图的抽样方案不同,它发现过程变差的灵敏度也会不同,子组到底应当多大呢?
这要根据你所要控制的过程的能力的大小和对控制图所期望的功效来确定。
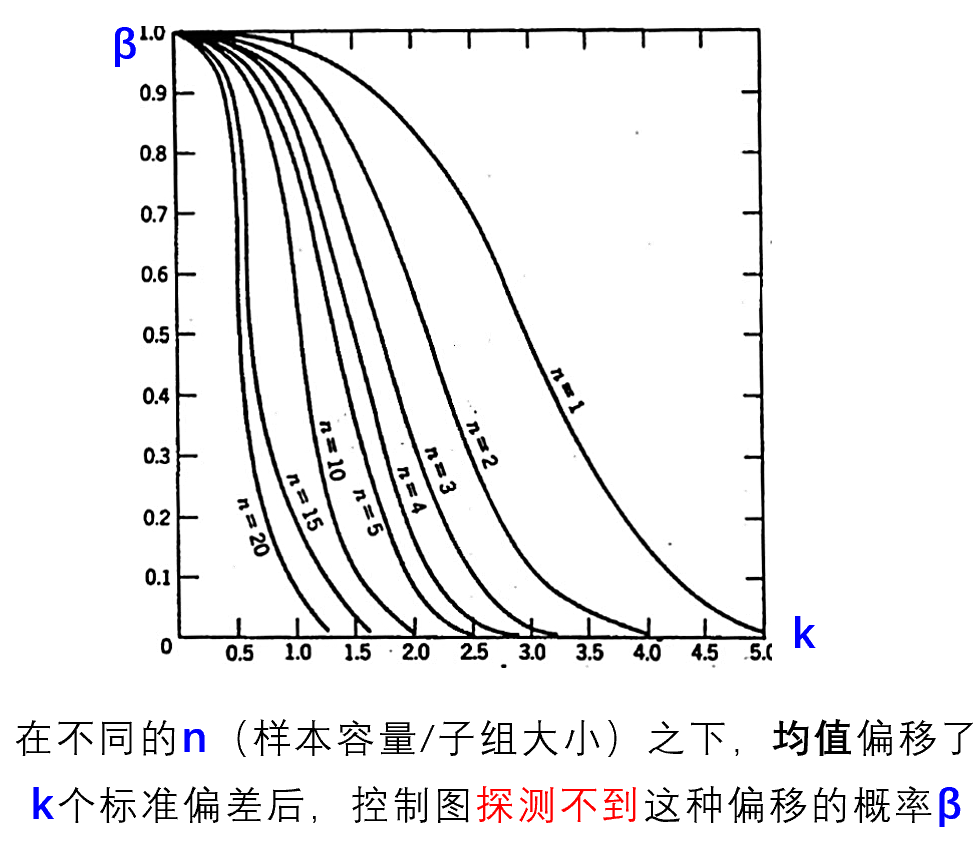
我们用6倍的过程标准差定义过程能力(注意:不是过程能力指数CPK)。过程能力越高,说明过程的变差越小,就需要越多的样本才能发现它的变差,反之,过程能力越低,只需要较少的样本就可以探测到过程变差了。打个比方,这就好比是一个班级里有一个2米以上的篮球运动员,要去找到这个运动员,只需要一个样本就可以了;而你去探测一个国旗仪仗队的队员之间的身高差异,你可能就要用高精度的尺子测量所有的队员才可以发现他们之间的身高差异。什么是控制图的功效呢?这里的功效指的是发现均值偏移了K个标准差的概率,如下图所示,其中,β是均值偏移了K个标准差后,控制图探测不到这个偏移的概率,所以1-β就是功效,即探测到这个偏移的概率。从该图中可以发出,要想获得较高的功效,就必须增加子组的大小。
为了确定子组大小,我们还要了解下面几个概念:
1、子组的间隔。它是指多长时间抽取一个子组,一般情况下是间隔相等的时间。但是,要注意,最好是在人、机、料、法、环(4M1E)交替的时候进行抽样,如班次交接时、机器开机或调整设置后、原材料批次变更时等,在这些节骨眼上生产出的产品的特性会有较高的变异机会。
2、受控ARL(平均运行长度)。它是指在没有实际失控的情况下,两次误报警信号之间的子组个数,它是一类错误概率的倒数,即
3、失控ARL。如果我们只使用失控判断准则1,即超出正负3个西格玛的控制限即为失控,则过程在统计受控状态下,均值点会有α=0.27%的概率落在控制限以外,即ARL=1/0.0027≈370,平均约370个点中会有一个点落在控制限以外,即使过程是统计受控的。3、失控ARL。它是指当均值图上有点发生失控后,在所发生的点上看不到这个失控,直到再抽若干次样后才在图上表现出来,这样的抽样次数为失控ARL。它是功效的倒数,即
4、过程性能指数PPK。在这里,我们还未使用控制图,不能判断过程是否受控,所以我们用PPK,而不是用CPK,CPK是过程受控状态下的能力指数。
另外,在确定子组大小之前,我们还要准备下列信息:
1、制造过程每天的运行小时(工作小时)数;
2、两次错误报警间的允许天数,以及从实际失控到发现时的天数,这是由工厂的管理者给出的,这也是对控制图的要求;
3、过程能力/性能指数目标值,这是客户或管理者要求的,假设为1.33,而现在假设实际的能力/性能指数为2.0。
于是,
我们第一步我们先确定子组间隔,如下图所示
第二步,我们确定计算所期望的控制图功效1-β,如下图所示
第三步,我们计算子组的大小,即每个子组的样本数量,我们在此借助于Minitab软件的“单样本Z的功效及样本量”功能,如下图所示
在此还需要说明的一点是,样本数据应当是正态或近似正态的,而且确保子组的均值间呈正态分布。而为了应对可能不够正态的问题,根据中心极限定理,我们需要子组的大小应尽可能多,在本例中应当大于3。 收起阅读 »
下面是我的回答,并在此基础上展开说明如何确定子组的大小。
这是SPC控制图的一个最基本的概念之一。在均值-极差图中,子组越大,则均值上下控制限之间越窄,也就是说,均值控制图越灵敏。这是因为,均值图的控制限公式为:总均值加/减3倍的均值标准差,即:
根据中心极限定理,均值标准差等于单值的标准差除以子组大小n的平方根,
也就是说,子组越大,则均值的标准差就越小,由此计算出来的均值上下限间就越窄。因此,每个子组抽样越多,即子组越大,则均值图上超出控制限的点会越多。
如果使用平均极差来计算控制限,我们可以发现A2这个系数也会随着子组大小的增加而减小。
子组的极差的大小,从理论上来讲,会随着子组大小的增加而增加,但是当子组中样本的数量大于9后,用极差来估计过程标准差时就不准确了,应当使用子组的标准差S来估计了。下图列出了不同子组大小之下,用子组的平均极差和平均标准差来估计过程标准差时的差异。
而当子组在9以下时,极差随子组大小的变化并没有那么明显,特别是当过程处于稳定的状态时候。
由此可见,控制图的抽样方案不同,它发现过程变差的灵敏度也会不同,子组到底应当多大呢?
这要根据你所要控制的过程的能力的大小和对控制图所期望的功效来确定。
我们用6倍的过程标准差定义过程能力(注意:不是过程能力指数CPK)。过程能力越高,说明过程的变差越小,就需要越多的样本才能发现它的变差,反之,过程能力越低,只需要较少的样本就可以探测到过程变差了。打个比方,这就好比是一个班级里有一个2米以上的篮球运动员,要去找到这个运动员,只需要一个样本就可以了;而你去探测一个国旗仪仗队的队员之间的身高差异,你可能就要用高精度的尺子测量所有的队员才可以发现他们之间的身高差异。什么是控制图的功效呢?这里的功效指的是发现均值偏移了K个标准差的概率,如下图所示,其中,β是均值偏移了K个标准差后,控制图探测不到这个偏移的概率,所以1-β就是功效,即探测到这个偏移的概率。从该图中可以发出,要想获得较高的功效,就必须增加子组的大小。
为了确定子组大小,我们还要了解下面几个概念:
1、子组的间隔。它是指多长时间抽取一个子组,一般情况下是间隔相等的时间。但是,要注意,最好是在人、机、料、法、环(4M1E)交替的时候进行抽样,如班次交接时、机器开机或调整设置后、原材料批次变更时等,在这些节骨眼上生产出的产品的特性会有较高的变异机会。
2、受控ARL(平均运行长度)。它是指在没有实际失控的情况下,两次误报警信号之间的子组个数,它是一类错误概率的倒数,即
3、失控ARL。如果我们只使用失控判断准则1,即超出正负3个西格玛的控制限即为失控,则过程在统计受控状态下,均值点会有α=0.27%的概率落在控制限以外,即ARL=1/0.0027≈370,平均约370个点中会有一个点落在控制限以外,即使过程是统计受控的。3、失控ARL。它是指当均值图上有点发生失控后,在所发生的点上看不到这个失控,直到再抽若干次样后才在图上表现出来,这样的抽样次数为失控ARL。它是功效的倒数,即
4、过程性能指数PPK。在这里,我们还未使用控制图,不能判断过程是否受控,所以我们用PPK,而不是用CPK,CPK是过程受控状态下的能力指数。
另外,在确定子组大小之前,我们还要准备下列信息:
1、制造过程每天的运行小时(工作小时)数;
2、两次错误报警间的允许天数,以及从实际失控到发现时的天数,这是由工厂的管理者给出的,这也是对控制图的要求;
3、过程能力/性能指数目标值,这是客户或管理者要求的,假设为1.33,而现在假设实际的能力/性能指数为2.0。
于是,
我们第一步我们先确定子组间隔,如下图所示
第二步,我们确定计算所期望的控制图功效1-β,如下图所示
第三步,我们计算子组的大小,即每个子组的样本数量,我们在此借助于Minitab软件的“单样本Z的功效及样本量”功能,如下图所示
在此还需要说明的一点是,样本数据应当是正态或近似正态的,而且确保子组的均值间呈正态分布。而为了应对可能不够正态的问题,根据中心极限定理,我们需要子组的大小应尽可能多,在本例中应当大于3。 收起阅读 »
石油和天然气行业中预测性SPC的威力
本文最初出现在The Minitab Blog
石油和天然气行业涉及持续产出的资本密集型过程。原油等原材料被大规模转化为石油产品,这使得过程控制变得至关重要。原材料的化学和物理性质往往具有很大的可变性,这可能会对过程输出产生显著的影响。工程师倾向于利用科学原理和经验来确定可能产生预期结果的工艺设置;然而,这种做法可能会不成功。统计过程控制图(SPC)对于指示变得不稳定的过程非常有用。使用SPC来提醒工艺转变的不利之处在于,可疑产品会同时产生。
制造商将检验原材料的大部分责任转移给了供应商。在收到材料之前,通常是在材料使用前几天或几周,将认证发送给客户是很常见的。如果供应商信息可用于在流程执行前预测流程转变,以考虑缓解措施,情况会怎样?本文解释了如何使用流程模型的操作部署来创建用于此目的的预统计流程图。还有许多其他行业的流程涉及资本密集型设备、连续流程和包含显著变化的原材料。食品、营养补充品和化学品的制造是可以从利用预测性SPC中获益的一些示例行业。
随着Minitab的最新发展,建模技术变得非常强大和易于使用。许多组织使用过程模型进行开发和改进。根据供应商测量和流程输入(由技术人员控制)创建流程模型,以确定与关键输出的关系。工程师找到正确的输入数量和模型类型,以便对输出做出合理的预测。该模型部署在模型操作并连接到新的数据流来进行预测。根据模型预测创建SPC图表,并监控其稳定性。如果识别出不利的趋势,则审查该模型以找到可以被操纵以减轻该趋势的过程变量。所有这些工作都在流程执行之前完成,这对于最小化质量风险非常有效。
该示例涉及16个连续变量,其中一个是由原材料发货前发送的供应商认证提供的度量。有离散变量,包括用于处理的单位和两个主要设置。利用逐步变量选择,从478行历史处理数据中创建了具有良好拟合性(r-square ~ 67%)的线性多元回归模型。
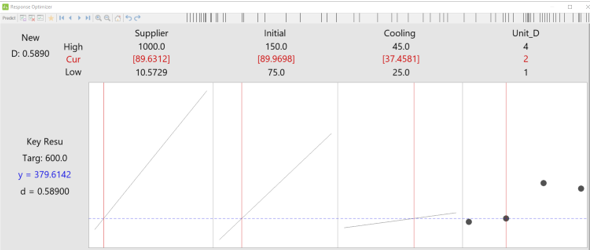
响应优化图说明了最重要的预测变量的杠杆作用。供应商认证措施和初始压力具有陡峭的线性关系,因为值的微小变化会在关键响应中产生显著差异。冷却温度指示较小的响应,并且单位的变化看起来对关键响应有分组影响。
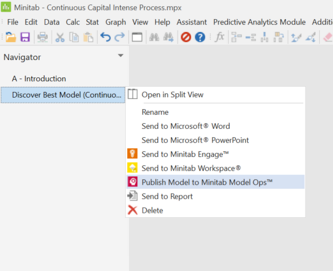
回归模型在预测历史数据的关键响应结果方面做得很好。工程师只需点击一下鼠标,就可以轻松地将模型从Minitab统计软件发布到ModelOps。
收集新数据,以便对关键输出进行预测。该数据包括来自供应商认证的测量值、设置的静态输入值,以及具有已知变化的过程变量的分布生成数据。加工温度是分布生成变量的一个例子。工程师知道过程点的实际温度会随着控制设置而变化。变量的参数是从设备制造商的过程测量点或技术规格创建的。从选定的分布计算变量,以获得实际的处理场景。这与蒙特卡洛模拟中使用的技术基本相同。
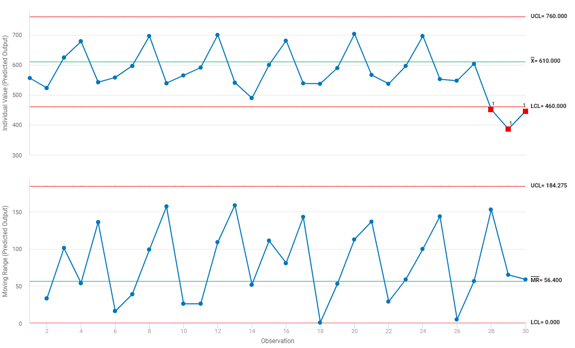
Minitab Connect轻松地每小时检索一次数据,并发送给模型运营部以获得预测。利用一个单独的移动范围控制图来监测趋势。确保使用历史参数计算统计控制限值非常重要;使用模拟数据来计算限值是不合适的。下图所示的预测SPC图说明了在最后3次观察之前的预期稳定过程。所有三个最终观察值都低于历史控制下限,如果不稳定的趋势持续下去,可能会产生质量问题。
工程团队审查过程模型,并确定初始压力很容易从90增加到120。模型优化器表明,控制设置的变化可能会减轻由于供应商认证措施的变化而导致的结果下降。在源数据表中完成对初始压力设置的建议更改,并重新启动Connect中的数据提取和制图。最终的图表确实提供了初始压力的变化减轻了供应商措施变化的负面影响的信息。
SPC的概念包括对导致不稳定的变化趋势的及时反应。不稳定的过程包含质量风险,可能导致不合格或降级的材料。在流程执行前根据数据创建流程控制图的能力非常有价值,因为现在有可能在产生任何实际结果之前减轻不利趋势。在石油和天然气行业,由于所生产产品的数量和潜在收入,收益可能高达数百万美元。Minitab解决方案使创建和监控预测性SPC的过程成为质量管理的重要组成部分。
本文最初出现在Minitab博客上。 收起阅读 »
石油和天然气行业涉及持续产出的资本密集型过程。原油等原材料被大规模转化为石油产品,这使得过程控制变得至关重要。原材料的化学和物理性质往往具有很大的可变性,这可能会对过程输出产生显著的影响。工程师倾向于利用科学原理和经验来确定可能产生预期结果的工艺设置;然而,这种做法可能会不成功。统计过程控制图(SPC)对于指示变得不稳定的过程非常有用。使用SPC来提醒工艺转变的不利之处在于,可疑产品会同时产生。
制造商将检验原材料的大部分责任转移给了供应商。在收到材料之前,通常是在材料使用前几天或几周,将认证发送给客户是很常见的。如果供应商信息可用于在流程执行前预测流程转变,以考虑缓解措施,情况会怎样?本文解释了如何使用流程模型的操作部署来创建用于此目的的预统计流程图。还有许多其他行业的流程涉及资本密集型设备、连续流程和包含显著变化的原材料。食品、营养补充品和化学品的制造是可以从利用预测性SPC中获益的一些示例行业。
随着Minitab的最新发展,建模技术变得非常强大和易于使用。许多组织使用过程模型进行开发和改进。根据供应商测量和流程输入(由技术人员控制)创建流程模型,以确定与关键输出的关系。工程师找到正确的输入数量和模型类型,以便对输出做出合理的预测。该模型部署在模型操作并连接到新的数据流来进行预测。根据模型预测创建SPC图表,并监控其稳定性。如果识别出不利的趋势,则审查该模型以找到可以被操纵以减轻该趋势的过程变量。所有这些工作都在流程执行之前完成,这对于最小化质量风险非常有效。
该示例涉及16个连续变量,其中一个是由原材料发货前发送的供应商认证提供的度量。有离散变量,包括用于处理的单位和两个主要设置。利用逐步变量选择,从478行历史处理数据中创建了具有良好拟合性(r-square ~ 67%)的线性多元回归模型。
响应优化图说明了最重要的预测变量的杠杆作用。供应商认证措施和初始压力具有陡峭的线性关系,因为值的微小变化会在关键响应中产生显著差异。冷却温度指示较小的响应,并且单位的变化看起来对关键响应有分组影响。
回归模型在预测历史数据的关键响应结果方面做得很好。工程师只需点击一下鼠标,就可以轻松地将模型从Minitab统计软件发布到ModelOps。
收集新数据,以便对关键输出进行预测。该数据包括来自供应商认证的测量值、设置的静态输入值,以及具有已知变化的过程变量的分布生成数据。加工温度是分布生成变量的一个例子。工程师知道过程点的实际温度会随着控制设置而变化。变量的参数是从设备制造商的过程测量点或技术规格创建的。从选定的分布计算变量,以获得实际的处理场景。这与蒙特卡洛模拟中使用的技术基本相同。
Minitab Connect轻松地每小时检索一次数据,并发送给模型运营部以获得预测。利用一个单独的移动范围控制图来监测趋势。确保使用历史参数计算统计控制限值非常重要;使用模拟数据来计算限值是不合适的。下图所示的预测SPC图说明了在最后3次观察之前的预期稳定过程。所有三个最终观察值都低于历史控制下限,如果不稳定的趋势持续下去,可能会产生质量问题。
工程团队审查过程模型,并确定初始压力很容易从90增加到120。模型优化器表明,控制设置的变化可能会减轻由于供应商认证措施的变化而导致的结果下降。在源数据表中完成对初始压力设置的建议更改,并重新启动Connect中的数据提取和制图。最终的图表确实提供了初始压力的变化减轻了供应商措施变化的负面影响的信息。
SPC的概念包括对导致不稳定的变化趋势的及时反应。不稳定的过程包含质量风险,可能导致不合格或降级的材料。在流程执行前根据数据创建流程控制图的能力非常有价值,因为现在有可能在产生任何实际结果之前减轻不利趋势。在石油和天然气行业,由于所生产产品的数量和潜在收入,收益可能高达数百万美元。Minitab解决方案使创建和监控预测性SPC的过程成为质量管理的重要组成部分。
本文最初出现在Minitab博客上。 收起阅读 »
SPC 之 I-MR 控制图
概述
1924 年,美国的休哈特博士应用统计数学理论将 3Sigma 原理运用于生产过程中,并发表了著名的“控制图法”,对产品特性和过程变量进行控制,开启了统计过程控制新时代。
什么是控制图
控制图指示过程何时不受控制,有助于标识是否存在特殊原因变异。如果存在特殊原因变异,则说明过程不稳定且有必要采取纠正措施。
控制图是按时间排序顺序绘制过程数据的图。大多数控制图都包括一条中心线、一个控制上限和一个控制下限。中心线表示过程均值。控制限表示过程变异。默认情况下,控制限绘制在中心线上下 3σ 的位置。
随机位于控制限内的点指示过程受控制且仅显示常见原因变异。位于控制限外部或者显示非随机模式的点指示过程不受控制且存在特殊原因变异。
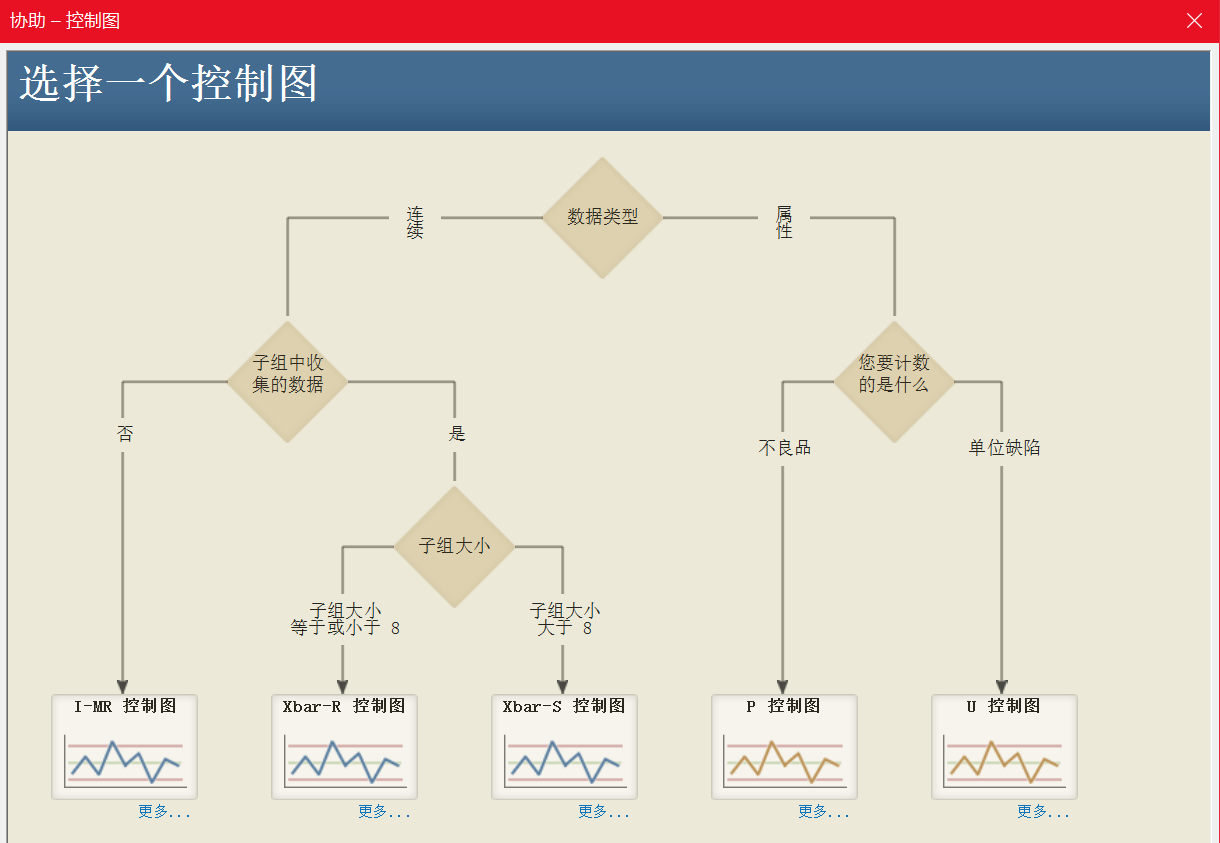
如何选择合适的控制图
随着控制图的发展,它的类型也是越来越多,那么这时候对于使用 Minitab 的朋友来说,经常会纠结如何去选择一个合适的控制图。在 Minitab 19 中,协助菜单可以很好的帮助我们去选择一个合适的控制图。
I-MR 控制图
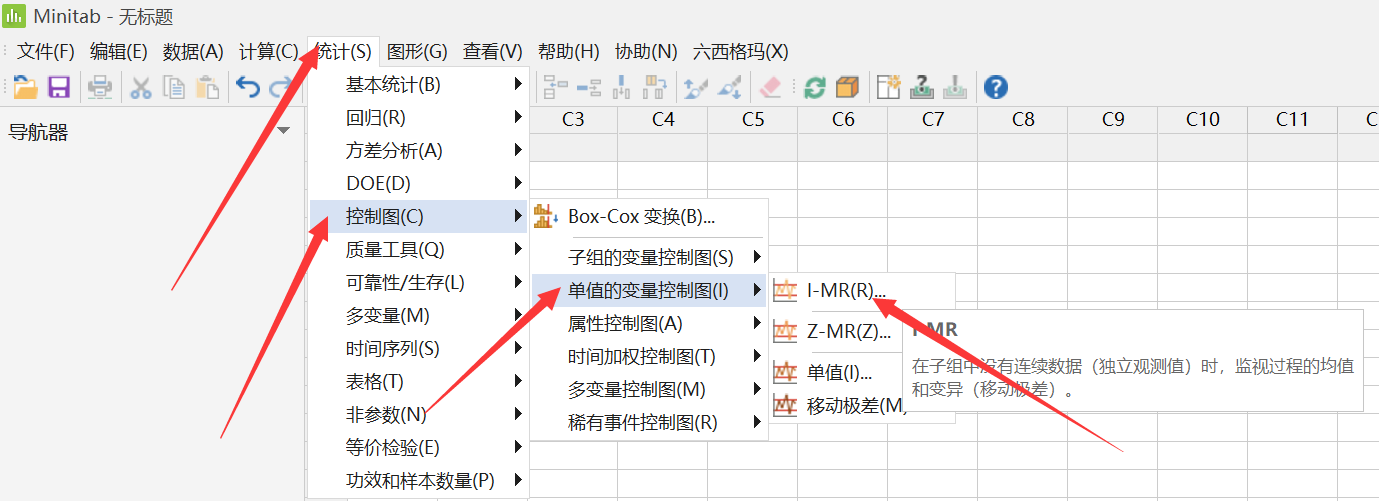
今天,我们来绘制一下 I-MR 控制图。
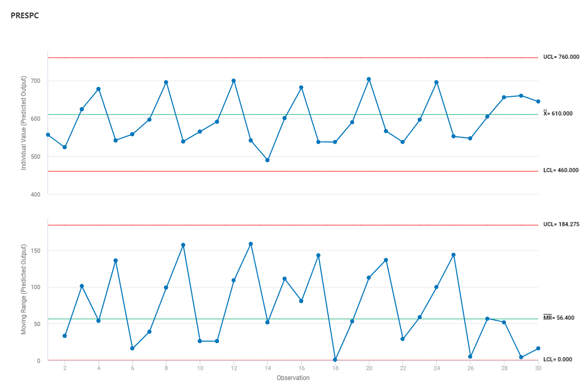
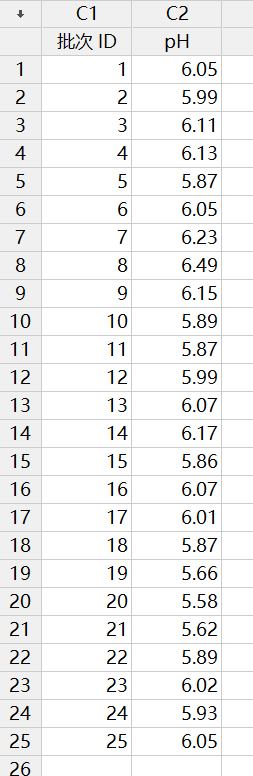
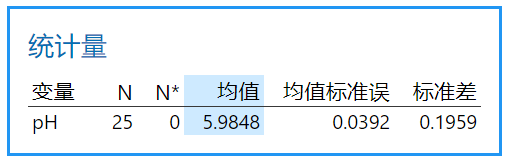
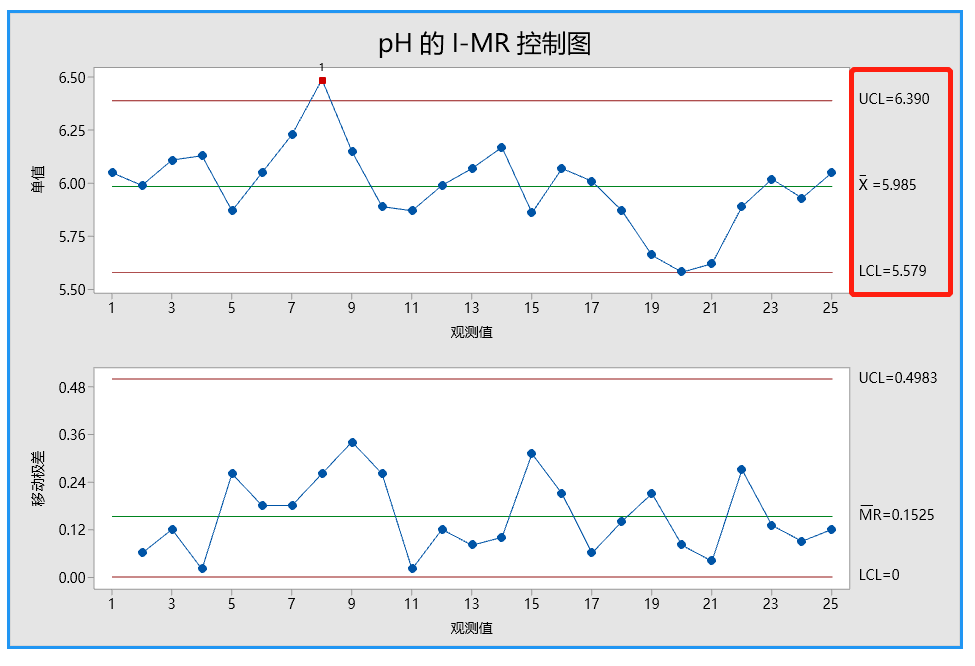
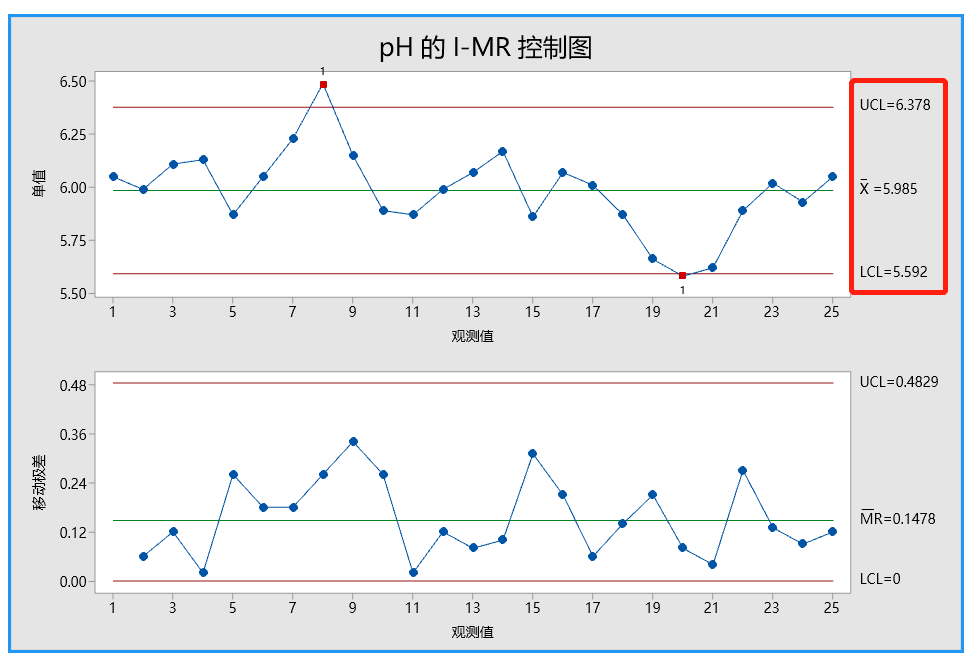
问题背景:某质量工程师监控了液体洗涤剂的生产过程,想要评估该过程是否受控制。这位工程师测量了 25 个连续批次的洗涤剂的 pH 值。
由于 pH 值的数据类型是连续型数据,而且是每批次只取一个样品(子组大小等于 1),故这位工程师创建了一张 I-MR 控制图,以监控洗涤剂的生产过程。
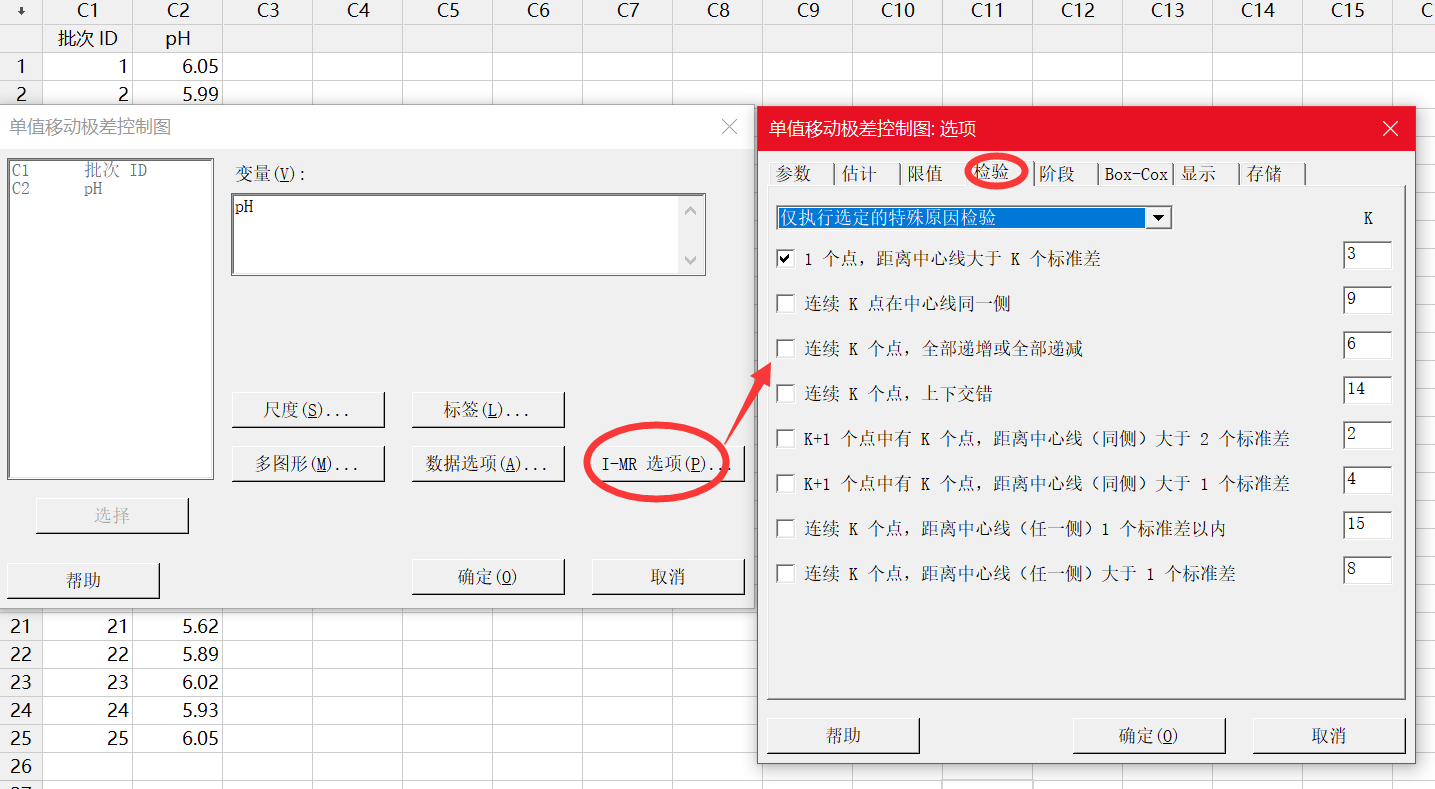
Minitab 绘制 I-MR 控制图
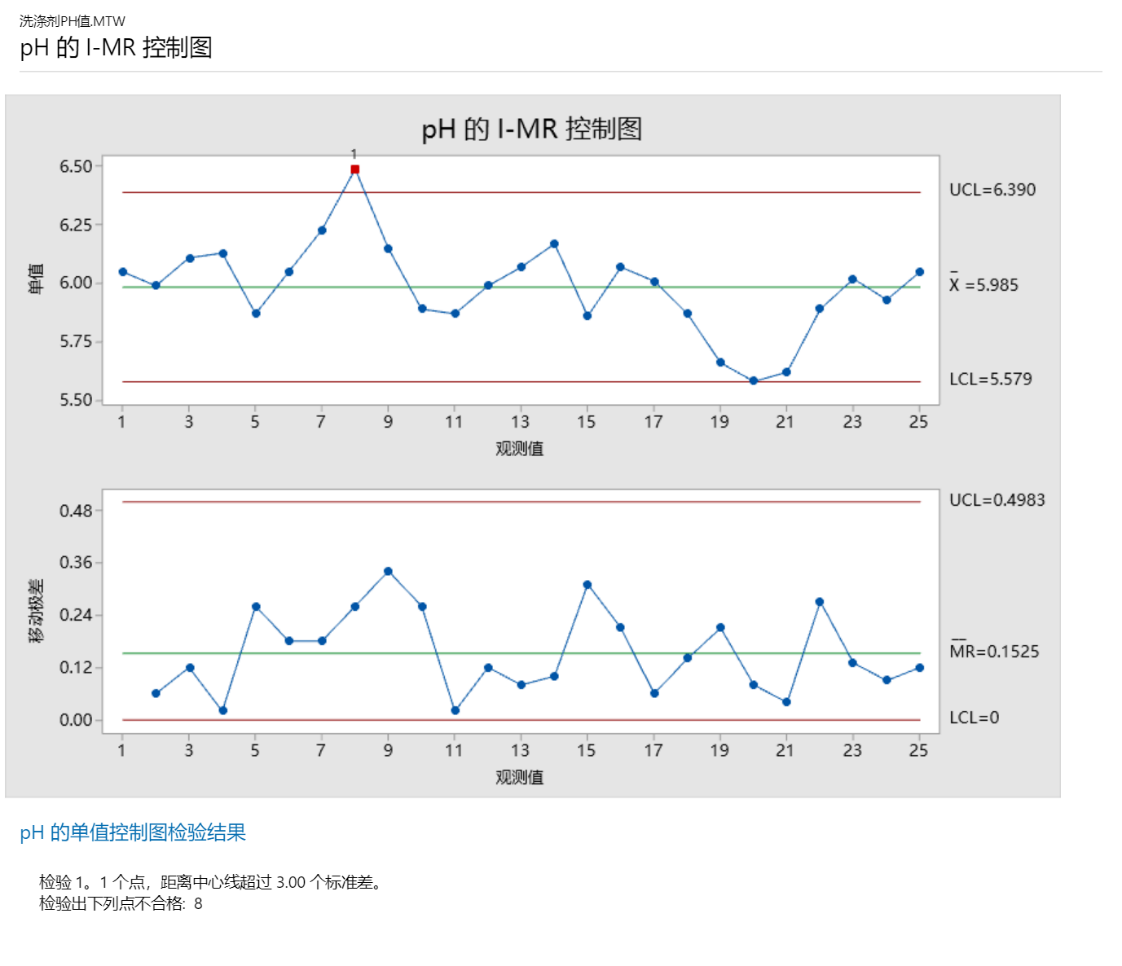
Minitab 结果解释
首先解释移动极差控制图(MR 控制图)以检查过程变异。没有位于控制限外部的点且所有的点都显示出随机模式。因此,过程变异受控制,质量工程师可以检查单值控制图(I 控制图)上的过程中心。
I 控制图上的一个观测值在检验 1 中失败,因为观测值在中心线上方且距离中心线超过 3个标准差。
I-MR 控制图的控制限计算(手动)
对于 I-MR 控制图,包含两张图单值控制图(I 控制图)和移动极差控制图(MR 控制图), 我们首先来认识一下这两张图形上的 X 轴、Y 轴、点和线分别表示什么含义。
一、单值控制图(I 控制图)
X 轴:批次 ID
Y 轴:单值(每个批次对应的 pH 值,如单值图上的第二个点表示的是批次 2 的 pH 值)
点:单值控制图(I 控制图)上的每个标绘点是单独的观测值(如上图)。
中心线:单值控制图(I 控制图)上的中心线是过程平均值的估计值,计算如下
控制限:单值控制图(I 控制图)控制限的计算结果取决于标准差的估计方式。
1)移动极差平均值(默认方法)-移动极差长度默认为 2
a. 计算移动极差 MR(相邻 2 个数的较大值减较小值),当前数据样本量为 25,计算得到24 个移动极差。
b. 计算这 24 个移动极差的平均值 MRbar
c. 估计标准差的公式如下:
控制限计算公式
其中 k 为检验 1 的参数。默认值为 3。
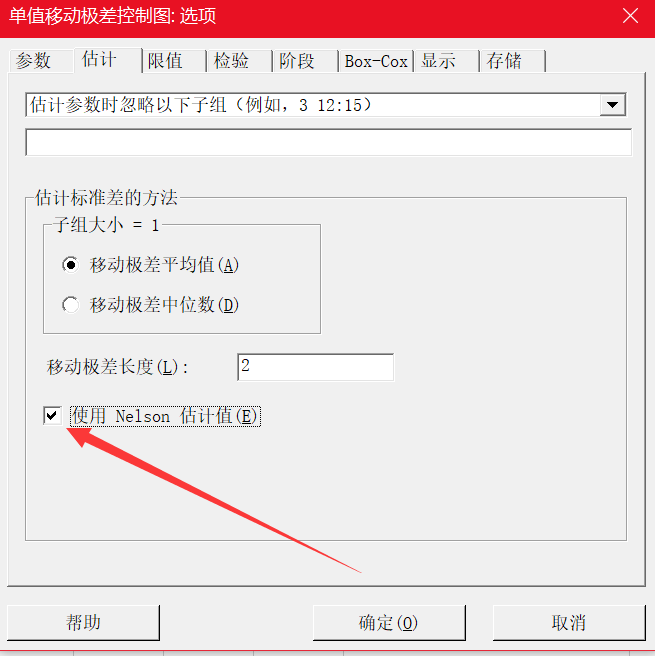
当选择默认的用移动极差平均值来估计标准差时,我们还可以勾选”使用 Nelson 估计值”。使用 Nelson 估计值可以在计算控制限时更正异常大的移动极差值。此过程与 Nelson1 提出的过程相似。Minitab 消除比移动极差平均值大 3σ 的任何移动极差值,然后重新计算移动极差平均值和控制限。
2)移动极差中位数
a. 计算移动极差
b. 计算移动极差中位数
c. 估计标准差的公式如下:
二、移动极差控制图(MR 控制图)
X 轴:批次 ID
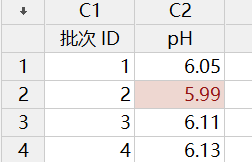
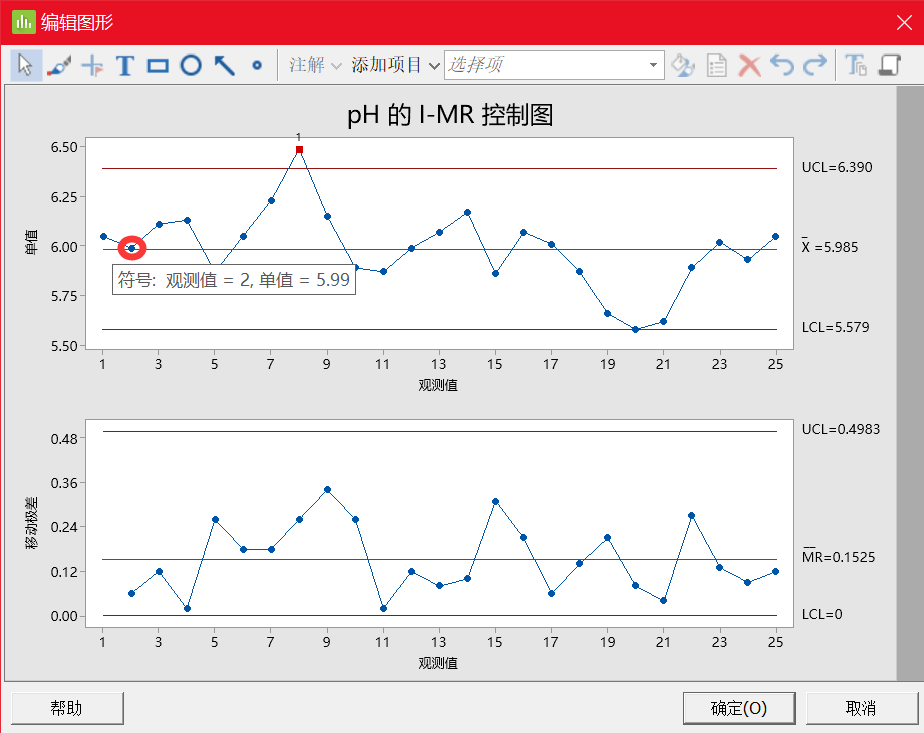
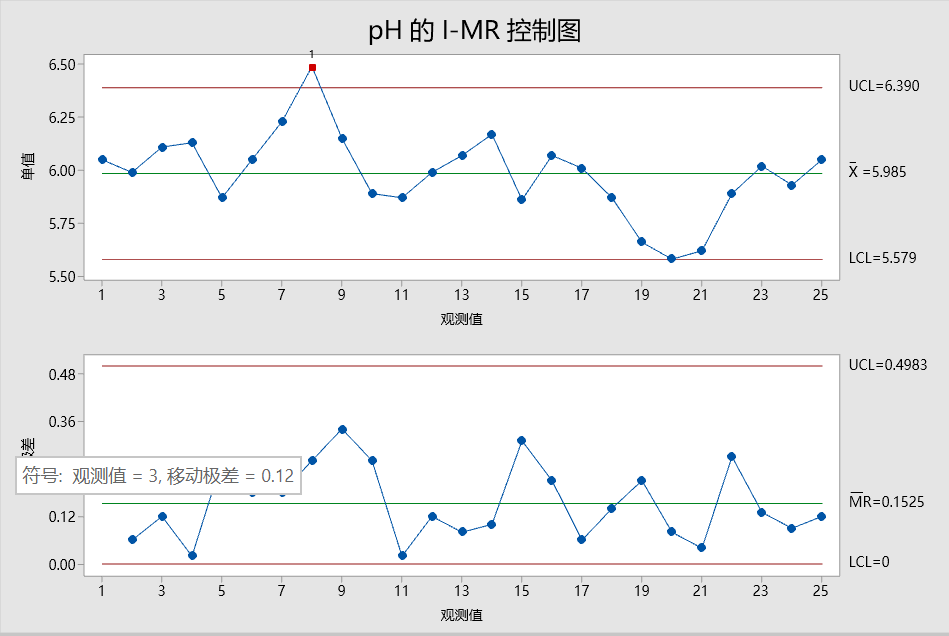
Y 轴:移动极差(如下 MR 控制图中的第二个点是批次 2 的 pH 值 5.99 和批次 3pH 值 6.11中较大值减去较小值,结果为 0.12(6.11-5.99)
点:MR 控制图上的标绘点是移动极差(移动极差是两个或多个连续点之间差值的绝对值)。
中心线:中心线是移动极差平均值的无偏估计值 MRbar
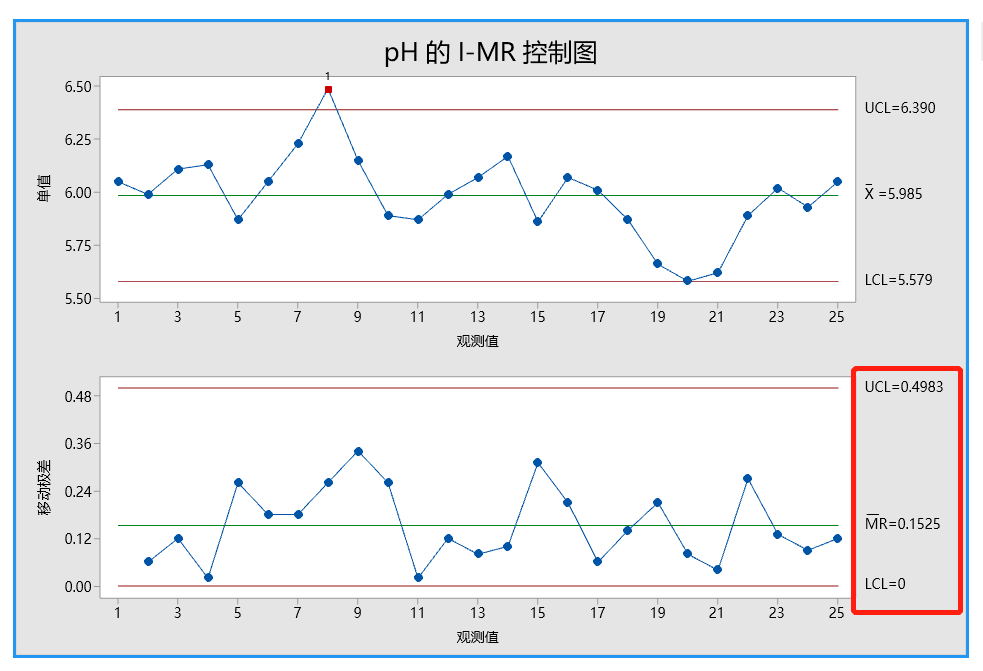
控制上限:??? = (??(?) ⋅ ?) + (? ⋅ ??(?) ⋅ ?)
控制下限:??? = (??(?) ⋅ ?) − (? ⋅ ??(?) ⋅ ?)或 LCL=0(计算结果为负值时)
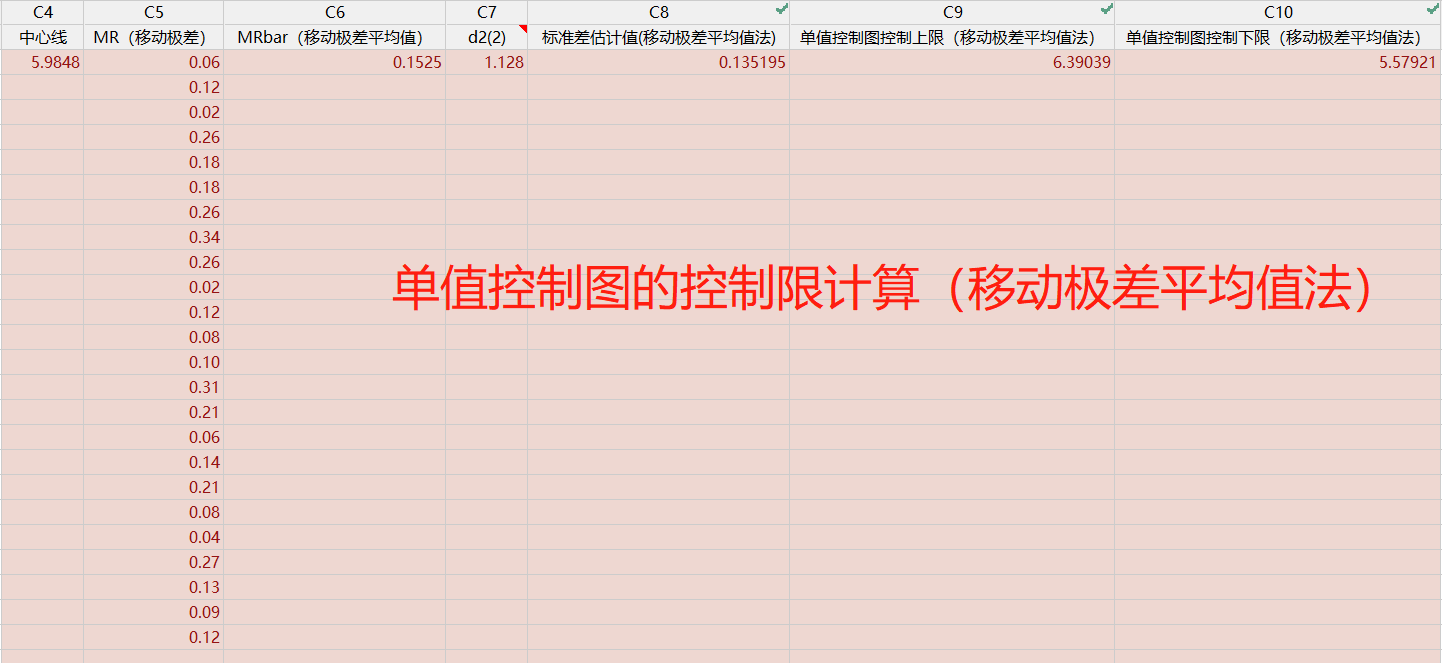
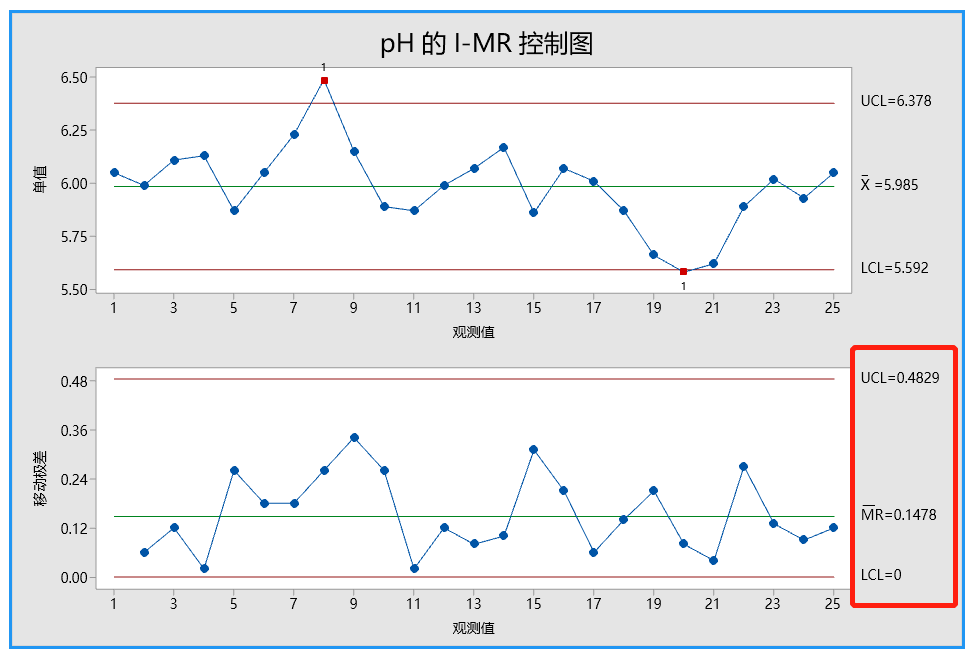
移动极差平均值法的结果
移动极差中位数法的结果
结论
手动计算的过程比较复杂,而且还可能会出错,但是有了 Minitab 的帮助,我们只需要选择好合适的控制图后,点击几下就可以高效快速的计算出对应的控制限。当然,花点时间手动计算一下这些值,能够帮助你更好的理解控制图。而且在计算的过程中,你也会发现 Minitab 的算法跟 Excel 中算法的差异,也能够发现单值控制图的控制限受到移动极差的影响,所以在分析这两张控制图时,应该先分析下面的移动极差控制图,移动极差控制图中没有异常点时,这时候分析单值控制图才是有意义的。
X 轴:批次 ID
Y 轴:移动极差(如下 MR 控制图中的第二个点是批次 2 的 pH 值 5.99 和批次3pH 值 6.11 中较大值减去较小值,结果为 0.12(6.11-5.99) 收起阅读 »
1924 年,美国的休哈特博士应用统计数学理论将 3Sigma 原理运用于生产过程中,并发表了著名的“控制图法”,对产品特性和过程变量进行控制,开启了统计过程控制新时代。
什么是控制图
控制图指示过程何时不受控制,有助于标识是否存在特殊原因变异。如果存在特殊原因变异,则说明过程不稳定且有必要采取纠正措施。
控制图是按时间排序顺序绘制过程数据的图。大多数控制图都包括一条中心线、一个控制上限和一个控制下限。中心线表示过程均值。控制限表示过程变异。默认情况下,控制限绘制在中心线上下 3σ 的位置。
随机位于控制限内的点指示过程受控制且仅显示常见原因变异。位于控制限外部或者显示非随机模式的点指示过程不受控制且存在特殊原因变异。
如何选择合适的控制图
随着控制图的发展,它的类型也是越来越多,那么这时候对于使用 Minitab 的朋友来说,经常会纠结如何去选择一个合适的控制图。在 Minitab 19 中,协助菜单可以很好的帮助我们去选择一个合适的控制图。
I-MR 控制图
今天,我们来绘制一下 I-MR 控制图。
问题背景:某质量工程师监控了液体洗涤剂的生产过程,想要评估该过程是否受控制。这位工程师测量了 25 个连续批次的洗涤剂的 pH 值。
由于 pH 值的数据类型是连续型数据,而且是每批次只取一个样品(子组大小等于 1),故这位工程师创建了一张 I-MR 控制图,以监控洗涤剂的生产过程。
Minitab 绘制 I-MR 控制图
Minitab 结果解释
首先解释移动极差控制图(MR 控制图)以检查过程变异。没有位于控制限外部的点且所有的点都显示出随机模式。因此,过程变异受控制,质量工程师可以检查单值控制图(I 控制图)上的过程中心。
I 控制图上的一个观测值在检验 1 中失败,因为观测值在中心线上方且距离中心线超过 3个标准差。
I-MR 控制图的控制限计算(手动)
对于 I-MR 控制图,包含两张图单值控制图(I 控制图)和移动极差控制图(MR 控制图), 我们首先来认识一下这两张图形上的 X 轴、Y 轴、点和线分别表示什么含义。
一、单值控制图(I 控制图)
X 轴:批次 ID
Y 轴:单值(每个批次对应的 pH 值,如单值图上的第二个点表示的是批次 2 的 pH 值)
点:单值控制图(I 控制图)上的每个标绘点是单独的观测值(如上图)。
中心线:单值控制图(I 控制图)上的中心线是过程平均值的估计值,计算如下
控制限:单值控制图(I 控制图)控制限的计算结果取决于标准差的估计方式。
1)移动极差平均值(默认方法)-移动极差长度默认为 2
a. 计算移动极差 MR(相邻 2 个数的较大值减较小值),当前数据样本量为 25,计算得到24 个移动极差。
b. 计算这 24 个移动极差的平均值 MRbar
c. 估计标准差的公式如下:
控制限计算公式
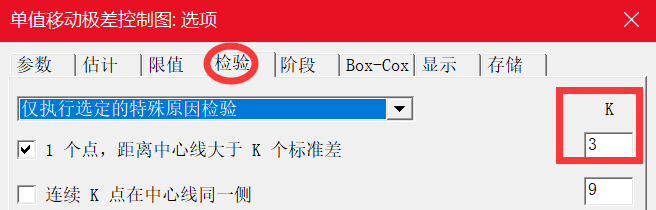
其中 k 为检验 1 的参数。默认值为 3。
当选择默认的用移动极差平均值来估计标准差时,我们还可以勾选”使用 Nelson 估计值”。使用 Nelson 估计值可以在计算控制限时更正异常大的移动极差值。此过程与 Nelson1 提出的过程相似。Minitab 消除比移动极差平均值大 3σ 的任何移动极差值,然后重新计算移动极差平均值和控制限。
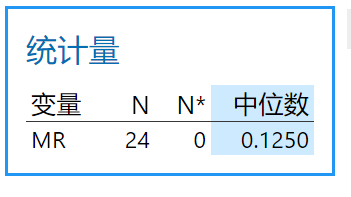
2)移动极差中位数
a. 计算移动极差
b. 计算移动极差中位数
c. 估计标准差的公式如下:
二、移动极差控制图(MR 控制图)
X 轴:批次 ID
Y 轴:移动极差(如下 MR 控制图中的第二个点是批次 2 的 pH 值 5.99 和批次 3pH 值 6.11中较大值减去较小值,结果为 0.12(6.11-5.99)
点:MR 控制图上的标绘点是移动极差(移动极差是两个或多个连续点之间差值的绝对值)。
中心线:中心线是移动极差平均值的无偏估计值 MRbar
控制上限:??? = (??(?) ⋅ ?) + (? ⋅ ??(?) ⋅ ?)
控制下限:??? = (??(?) ⋅ ?) − (? ⋅ ??(?) ⋅ ?)或 LCL=0(计算结果为负值时)
移动极差平均值法的结果
移动极差中位数法的结果
结论
手动计算的过程比较复杂,而且还可能会出错,但是有了 Minitab 的帮助,我们只需要选择好合适的控制图后,点击几下就可以高效快速的计算出对应的控制限。当然,花点时间手动计算一下这些值,能够帮助你更好的理解控制图。而且在计算的过程中,你也会发现 Minitab 的算法跟 Excel 中算法的差异,也能够发现单值控制图的控制限受到移动极差的影响,所以在分析这两张控制图时,应该先分析下面的移动极差控制图,移动极差控制图中没有异常点时,这时候分析单值控制图才是有意义的。
X 轴:批次 ID
Y 轴:移动极差(如下 MR 控制图中的第二个点是批次 2 的 pH 值 5.99 和批次3pH 值 6.11 中较大值减去较小值,结果为 0.12(6.11-5.99) 收起阅读 »
样本量大于30就可以认为是正态分布吗?你可能对中心极限定理有误区!
我经常会被问到这么一个问题:样本量多大就不用进行正态性检验了。殊不知,这问题的本身就是错误的,并不是样本大,就一定要服从正态分布。我们可以轻易举出一个反例来说明这个问题。比方说就用1-1000这一千个(甚至更多)自然数,组成一个样本,那么这个样本的分布就不是正态分布,因为1-1000服从的是均匀分布。另外,数据的分布基于形成的机理,有的分布天生就非正态(如寿命数据)。
但有些朋友,并不觉得这是一个错误的问题,甚至在他们的学习中还流传着这么一个说法:样本量大于30就可以认为是服从正态分布。当你向他问为什么的时候,会得到一个专业的解释——中心极限定理。
中心极限定理
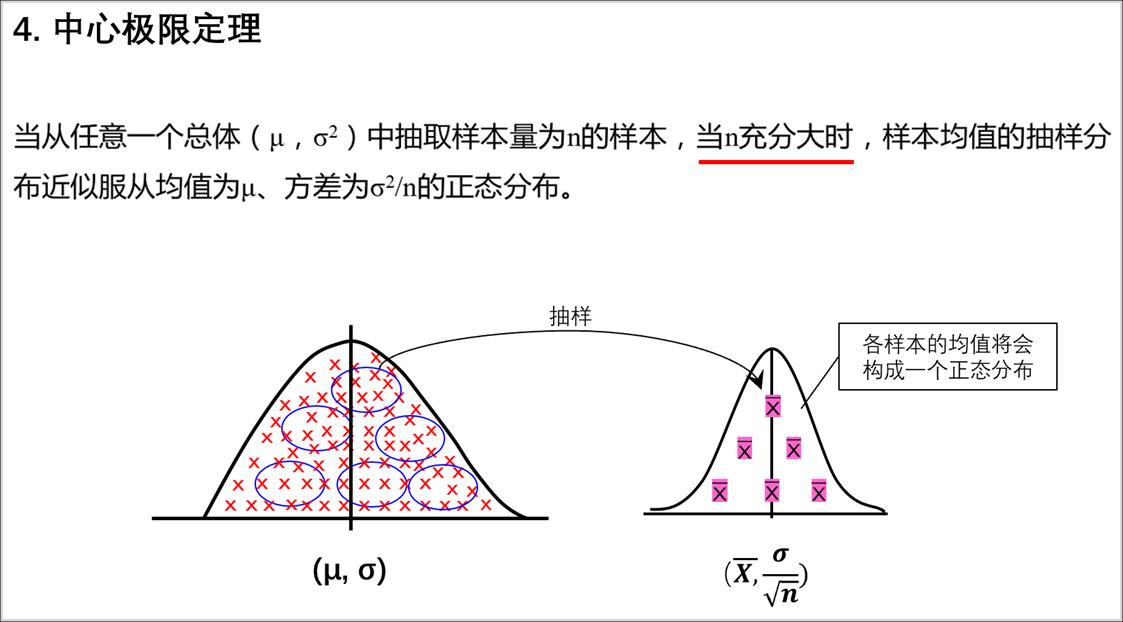
中心极限定理(Central Limit Theorem)是统计学中最重要的结论之一。在这里,我并不想给出中心极限定理专业的定义,只需要了解它告诉我们:来自某总体的一个样本,无论该总体服从什么分布,只要样本容量足够大,其样本均值都近似服从正态分布。
请注意这里的说法:“样本均值“近似正态,而不是样本本身服从正态(不是说你抽了30个样品组成的样本数据就正态)。这里又有一个大家疑惑的地方,样本容量足够大,多大才是足够大?这个问题的答案和总体分布的形状相关,如果样本本是来自近似对称分布的总体,那么当样本量取相当小(如样本量取5)的值的时候,正态逼近的结果也会非常好。然后,如果总体的分布严重倾斜,则样本量必须取相当大的值。根据检验,对于大多数总体来说,样本容量取30或者更大,就足以得到令人满意的正态逼近结果。我想这可能就是错误认为样本量大于30就认为是正态分布的出处了。
模拟掷骰子展示中心极限定理
为了展示中心极限定理,模拟多次投掷骰子来说明。
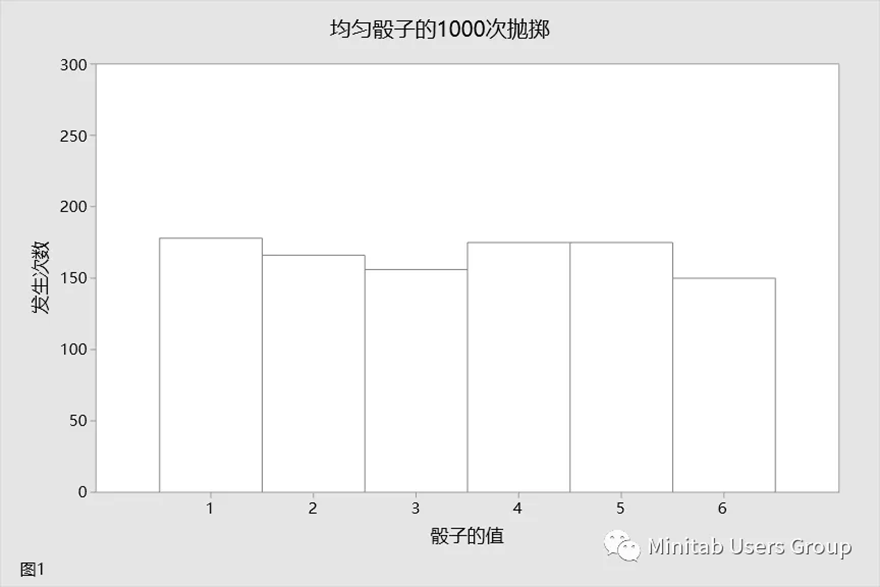
假设您掷骰子 1000 次。您希望得到相等数目的 1、2 等。让我们查看 1000 次骰子的分布(图1)。
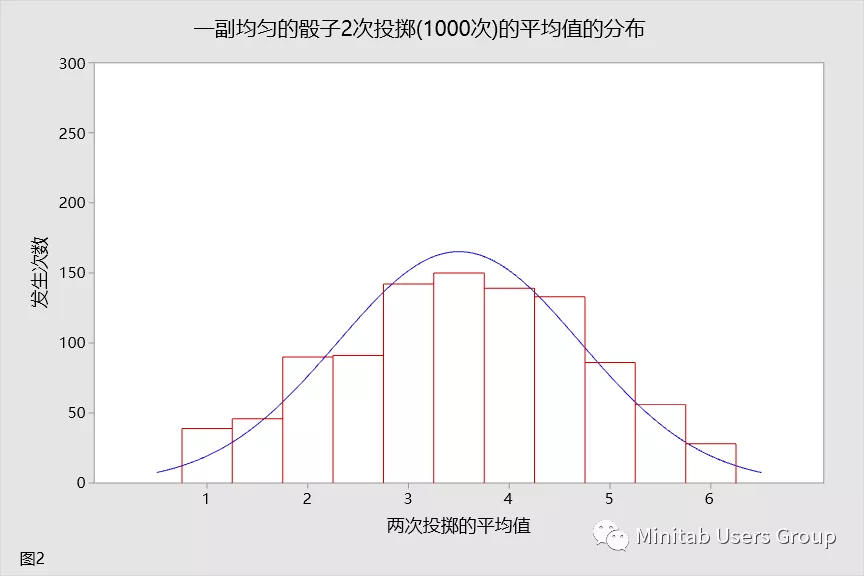
现在假设您将投掷 2 次,并采用两次投掷的平均值。您还将重复此试验 1000 次。让我们来看看两次投掷的平均值的分布。这种分布如图 2 所示。您是否注意到在只进行了两次投掷的情况下,平均值的分布已经呈现出了土堆形?
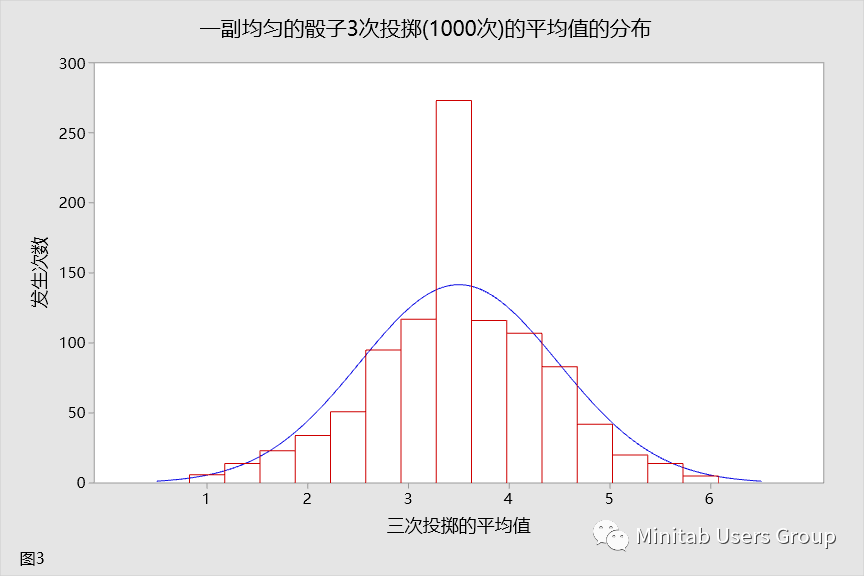
假设您现在投掷骰子三次,然后取三次投掷的平均值。再次重复此试验 1000 次。让我们来看看此举对投掷的平均值分布有何影响。这种分布如图 3 所示。同样,分布的形状与正态分布的形状相当接近。您是否注意到分布上发生了其他变化?
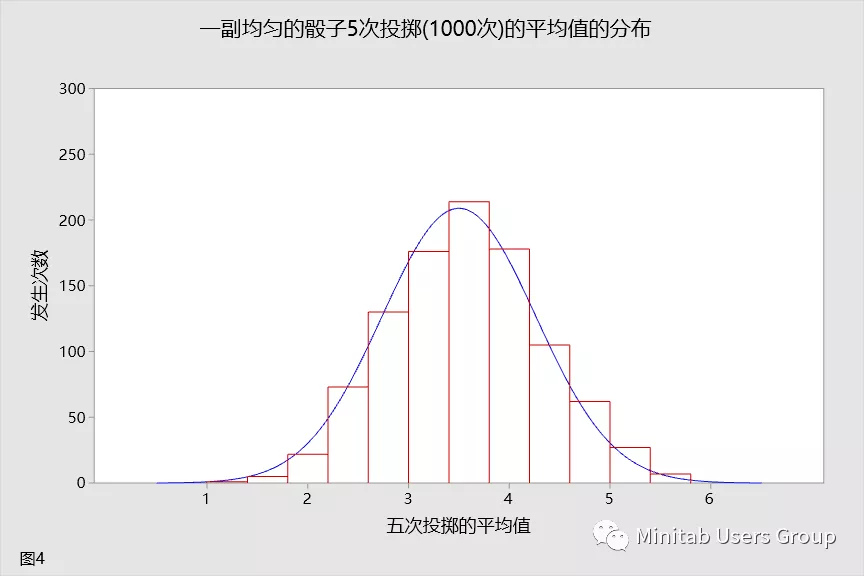
让我们投掷骰子五次,并取其平均值。再次重复此试验 1000 次。这种分布如图 4 所示。您是否已开始注意到所发生的情形中存在任何模式?
让我们继续增加平均投掷次数。此时您将投掷 10 次,并采用 10 次投掷的平均值。这种分布如图 5 所示。
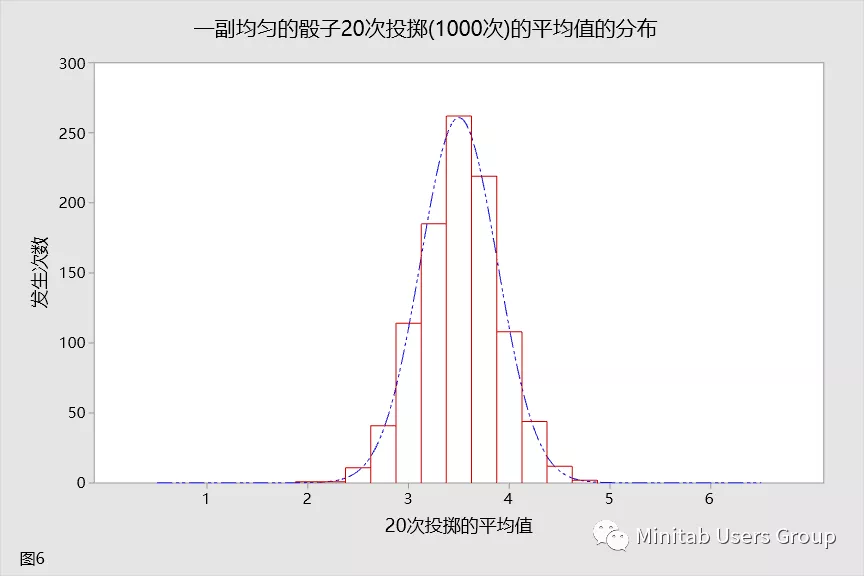
现在,随着您增加投掷次数,将看到两个现象。首先,您会看到,平均分布的形状开始与正态分布的形状相似。其次,您会看到,随着投掷次数的增加,分布变得越来越窄。让我们继续增加投掷次数。此时,您将投掷骰子 20 次。这种分布如图 6 所示。
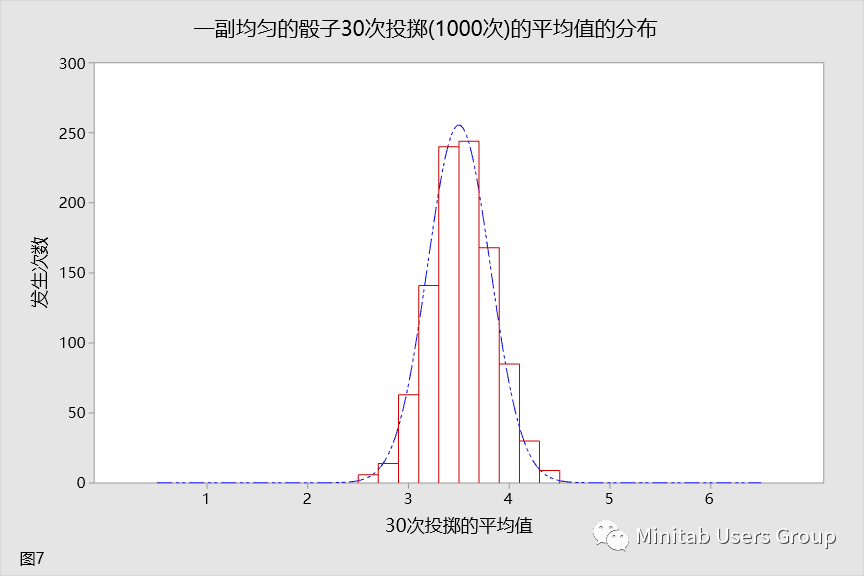
到现在,您应该确信增大样本数量对样本平均值分布是有影响的。您将再次增大样本数量,以强化这种认知。此时,您将投掷骰子 30 次。这种分布如图 7 所示。
让我们看看所呈现的情况,在一个图中绘制大小为 2、5、10、20、30 的样本的直方图,以查看变化的分布。
从上面的模拟结果,可以知道,当样本量大于30的时候,那么样本均值(取了1000次样本,得到1000个均值)的分布基本呈正态分布。
另外该定理还指出,如果根据总体不断重复绘制随机样本数量 n 以及有限均值 mu(y) 和标准差 sigma(y),然后在 n 较大时,样本均值的分布将近似呈正态分布,并且均值等于 mu(y),标准差等于 (sigma(y))/sqrt(n)。 收起阅读 »
但有些朋友,并不觉得这是一个错误的问题,甚至在他们的学习中还流传着这么一个说法:样本量大于30就可以认为是服从正态分布。当你向他问为什么的时候,会得到一个专业的解释——中心极限定理。
中心极限定理
中心极限定理(Central Limit Theorem)是统计学中最重要的结论之一。在这里,我并不想给出中心极限定理专业的定义,只需要了解它告诉我们:来自某总体的一个样本,无论该总体服从什么分布,只要样本容量足够大,其样本均值都近似服从正态分布。
请注意这里的说法:“样本均值“近似正态,而不是样本本身服从正态(不是说你抽了30个样品组成的样本数据就正态)。这里又有一个大家疑惑的地方,样本容量足够大,多大才是足够大?这个问题的答案和总体分布的形状相关,如果样本本是来自近似对称分布的总体,那么当样本量取相当小(如样本量取5)的值的时候,正态逼近的结果也会非常好。然后,如果总体的分布严重倾斜,则样本量必须取相当大的值。根据检验,对于大多数总体来说,样本容量取30或者更大,就足以得到令人满意的正态逼近结果。我想这可能就是错误认为样本量大于30就认为是正态分布的出处了。
模拟掷骰子展示中心极限定理
为了展示中心极限定理,模拟多次投掷骰子来说明。
假设您掷骰子 1000 次。您希望得到相等数目的 1、2 等。让我们查看 1000 次骰子的分布(图1)。
现在假设您将投掷 2 次,并采用两次投掷的平均值。您还将重复此试验 1000 次。让我们来看看两次投掷的平均值的分布。这种分布如图 2 所示。您是否注意到在只进行了两次投掷的情况下,平均值的分布已经呈现出了土堆形?
假设您现在投掷骰子三次,然后取三次投掷的平均值。再次重复此试验 1000 次。让我们来看看此举对投掷的平均值分布有何影响。这种分布如图 3 所示。同样,分布的形状与正态分布的形状相当接近。您是否注意到分布上发生了其他变化?
让我们投掷骰子五次,并取其平均值。再次重复此试验 1000 次。这种分布如图 4 所示。您是否已开始注意到所发生的情形中存在任何模式?
让我们继续增加平均投掷次数。此时您将投掷 10 次,并采用 10 次投掷的平均值。这种分布如图 5 所示。
现在,随着您增加投掷次数,将看到两个现象。首先,您会看到,平均分布的形状开始与正态分布的形状相似。其次,您会看到,随着投掷次数的增加,分布变得越来越窄。让我们继续增加投掷次数。此时,您将投掷骰子 20 次。这种分布如图 6 所示。
到现在,您应该确信增大样本数量对样本平均值分布是有影响的。您将再次增大样本数量,以强化这种认知。此时,您将投掷骰子 30 次。这种分布如图 7 所示。
让我们看看所呈现的情况,在一个图中绘制大小为 2、5、10、20、30 的样本的直方图,以查看变化的分布。
从上面的模拟结果,可以知道,当样本量大于30的时候,那么样本均值(取了1000次样本,得到1000个均值)的分布基本呈正态分布。
另外该定理还指出,如果根据总体不断重复绘制随机样本数量 n 以及有限均值 mu(y) 和标准差 sigma(y),然后在 n 较大时,样本均值的分布将近似呈正态分布,并且均值等于 mu(y),标准差等于 (sigma(y))/sqrt(n)。 收起阅读 »
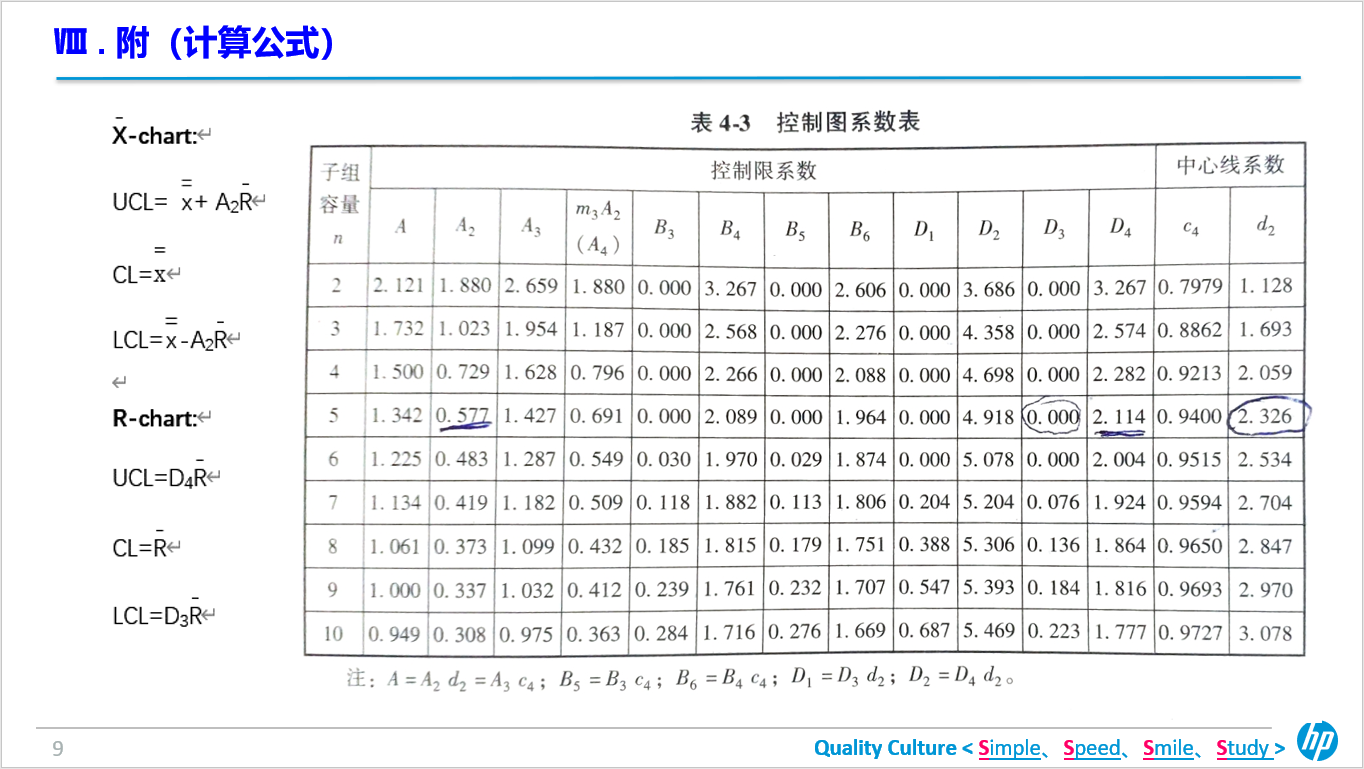
优思学院|SPC控制图中的控制线应该用"3倍标准差"还是用"系数A2、D3、D4"公式来计算?
有在学习六西格玛的小伙伴提问:SPC控制图中有的用系数A2、D3、D4来计算控制线,有的用3倍标准差来算,到底哪个是准确的?区别在什么?常数表中的A2、D3、D4是怎么得来的?
其实,SPC控制图的控制线并不存在两种方法来计算,从理论上来说,控制线的上下限是就是3倍总体标准差(实际的分布)。不过,由于我们一般没办法知道总体的标准差,所以实际上我们是不能通过3倍标准差的那些公式来计算上下限的。
例如,你可能收集了的25组数据,每组5个数据,一共125个数据,你想透过计算这些数据的标准差,再用来计算控制线的上下限,但这是不正确的,因为这个实际上是样本的标准差,而不是总体的标准差。
你只能根据你已经有的有限样本数据来推算出来,那就需要使用A2、D3、D4等常数,通过所知道的样本数量和平均值来推算。
想了解更多六西格玛工具的知识和应用方法,那就要关注优思学院,我们会不停期解答网友和同学的疑问,提供不同的管理知识~ 收起阅读 »
其实,SPC控制图的控制线并不存在两种方法来计算,从理论上来说,控制线的上下限是就是3倍总体标准差(实际的分布)。不过,由于我们一般没办法知道总体的标准差,所以实际上我们是不能通过3倍标准差的那些公式来计算上下限的。
例如,你可能收集了的25组数据,每组5个数据,一共125个数据,你想透过计算这些数据的标准差,再用来计算控制线的上下限,但这是不正确的,因为这个实际上是样本的标准差,而不是总体的标准差。
你只能根据你已经有的有限样本数据来推算出来,那就需要使用A2、D3、D4等常数,通过所知道的样本数量和平均值来推算。
想了解更多六西格玛工具的知识和应用方法,那就要关注优思学院,我们会不停期解答网友和同学的疑问,提供不同的管理知识~ 收起阅读 »
《两种质量诊断理论及其应用》阅后感
《两种质量诊断理论及其应用》阅后感
休哈特质控图运用了近百年,很少被质疑。但张公绪认为其适用前提是:多工序加工的首工序或与上工序独立不相关的后工序。多数上工序质量会影响下工序质量(简称“上影”),所以下工序质控图反映的是混杂了“上影”的“总质量”,并非表达下工序真正“分质量”。而要厘清下工序分质量,需张氏选控图剔除上影的相关性:即协方差。
这颠覆了前工序稳态,最终产品也稳态的认知。如对下工序用休哈特质控图监控:
下工序分质量正常(用选控图),上影正常,但二者方向相同而叠加,使下工序的质控图总质量呈异常,即虚报。
下工序分质量异常(用选控图),上影正常,但二者方向相反,叠加而抵消,使下工序质控图总质量呈正常,即漏报。
上述仅上下两工序的相关性,对于多工序:如10个变量,有45个协方差的矩阵。
多指标相互间的相关性、多工序,尤其在化工管道工序连续生产工艺,前工序对后几道工序相关性更复杂。如分别对各指标、各工序用休哈特质控图监控,忽略其相关性可能会出错。
如管道生产化工案例又加上多指标相关,的确是难题。
收起阅读 »
休哈特质控图运用了近百年,很少被质疑。但张公绪认为其适用前提是:多工序加工的首工序或与上工序独立不相关的后工序。多数上工序质量会影响下工序质量(简称“上影”),所以下工序质控图反映的是混杂了“上影”的“总质量”,并非表达下工序真正“分质量”。而要厘清下工序分质量,需张氏选控图剔除上影的相关性:即协方差。
这颠覆了前工序稳态,最终产品也稳态的认知。如对下工序用休哈特质控图监控:
下工序分质量正常(用选控图),上影正常,但二者方向相同而叠加,使下工序的质控图总质量呈异常,即虚报。
下工序分质量异常(用选控图),上影正常,但二者方向相反,叠加而抵消,使下工序质控图总质量呈正常,即漏报。
上述仅上下两工序的相关性,对于多工序:如10个变量,有45个协方差的矩阵。
多指标相互间的相关性、多工序,尤其在化工管道工序连续生产工艺,前工序对后几道工序相关性更复杂。如分别对各指标、各工序用休哈特质控图监控,忽略其相关性可能会出错。
如管道生产化工案例又加上多指标相关,的确是难题。
收起阅读 »
SPC应用案例
各位大侠好,这是我目前推行的供应商方的SPC管理初步案例
请大家指正,我这样推行的思路对不对。
欢迎大家留言讨论。
图1是其中1个改善案例,
图2是推行的系统化管理一角。
请大家指正,我这样推行的思路对不对。
欢迎大家留言讨论。
图1是其中1个改善案例,
图2是推行的系统化管理一角。
优思学院|"共同原因"和"特殊原因"是什么?
原发表于优思学院知乎号
如果你有看过优思学院关于SPC的六西格玛绿带课程视频,应该会知道在控制界限以内的变异原因,和超出控制界限以外的变异原因两者的区别。这是休哈特(Walter A. Shewhart)博士在 1924年发明第一张质量控制图时,给予的区分,他把两者分别命名为机遇原因(Chance Cause)和非机遇原因(Assignable Cause)。当时的学者为崇敬Shewhart博士把统计学应用在工业上所作的贡献,故亦有称为Shewhart图。
直到1970年,美国的质量管理大师 W. Edwards Deming博士首次应邀访台,在他所发表的学术演讲中,他提出了两个崭新的名词,就是在控制界限以内变异的原因,称为共同原因(Common Cause),超出控制界限以外的变异原因,称为特殊原因(Special Cause)。优思学院看到许多美英等国的质量管理书籍上,也逐渐采用这个名词。尤其近几年来,Deming博士时有新著问世,声望陡增,已成为质量管理界中之牛耳。
我们当时都以为Deming博士把共同原因来代替机遇原因,特殊原因来代替非机遇原因,无非是取其浅显达意,容易明白而已。而且一直以为这两个名词是相等的(即:共同原因 = 机遇原因,特殊原因 = 非机遇原因),没有再去作进一步的研究。
近十年来,美国新出版的质量管理书籍很多,也曾讨论过这些名词的问题,才知道这两个名词并不完全相等,因为Shewhart和Deming两人的出发点,并不一样。兹就读书所得,说明于次。
Shewhart博士的观念是着眼于制程中的变异,凡是在控制下的变异(Controlled Variation),可以认为是稳定(Stable)而经常存在的,所以称之为机遇原因,亦有人称之为无法避免之原因(Unavoidable Cause)者。这种变异是制程中固有的(Inherent)的变异,如果要把它减少(或减小),制程亦必随之而变动。
至于制程中不能控制的变异(Uncontrolled Variation),是随时在变动,既不稳定,亦非经常存在,并不是制程中的一部分。这种不稳定的性质,使制程不能按照预定的目标操作,致产生过多的变异(Excess Variation)。这种变异原因称为非机遇原因,应该可以把这种变异原因找出来,并加以消除掉,使制程回复正常。故这种原因亦有称之为可避免之原因(Avoidable Cause)者。
上述两种方法,都可以用来改进制程,但基本上是不同的。前者是去修改(改善) (Modify)一个经常而稳定的制程,而后者是去创造(Create)一个经常而稳定的制程。到底要采用那一种方法?就要看制程中的变异而定。因此,改进制程的首要步骤,是先要决定制程中有无不能控制的变异原因存在。而Shewhart的质量控制图是根据机率原理和统计学而来的,正是判断制程中有无不能控制的变异原因的有效利器。
至于Deming博士,他的着眼点是放在:谁该对这种变异负责?于是创造了共同原因和特殊原因这两个名词。
共同原因的变异是存在于制造系统(System)或控制良好的系统中。优思学院认为因为这种变异是属于系统内的,所以应该由控制这一系统的人员来负责,那即是:经理人员─特别是高阶层的经理人员。共同原因的变异仅祇能由经理阶层人员采取行动,才能把它移除掉。
特殊原因的变异在本质上是局部的。Deming博士曾说过,他喜欢用〝特殊〞这个形容词来指特定的一群作业员,或特定的某一位作业员,或特定的机器,或特定的局部环境等所造成的特殊原因。他并说,名词并不重要,重要的是观念。一般都能从发生问题的那一特定阶层人员,就可自行找出原因,采取行动,并把困扰的问题消除掉。
这些非机遇原因可以由作业员或那一部分的领班来采取行动。 而共同原因却不然,它可以是机遇原因,也可以是非机遇原因。无论在那一种情况,都是系统上发生的错误(Faults),仅祇能由经理阶层人员采取行动,才能改正过来。 Deming博士是着重在谁该对这种不同型式的变异负责,现在优思学院可以用一句话来说明他的观念:减少任何一个质量特性(如厚度,或绩效等)的变异,不管这个质量特性是否在控制状态之下,甚至只有少数几个或没有不良品产生,都认为是良好的管理。 〝零缺点〞并不能算够好。
工业界必须做到比符合规格还要来得好。经理人员要去研究制程,并且应该去找寻变异的来源,进而把它消除掉,以经常改进产品。质量控制图正是用来找出这些来源的有效利器。当制程中的变异减小后,则零件将更为相似,产品亦将愈佳。这些都是Deming博士在1950年带给日本人的金玉良言,日本人懂得这些话,经过了石川一郎(按:即石川馨氏之尊翁)及小柳贤一等继续不断地努力,才奠定了实施SQC成功的基础。
现在,将再介绍另一个观念(Concept),那就是:工程上(Engineering)对变异的观念,和Shewhart博士(包括Deming博士)对变异的观念,两者完全不同。工程上对变异的观念,其目的是要求产品能符合规格,不管产品中的变异有多大,只要在规格范围以内,就尽可能地让它去变化(Vary)。如果结果是在规格范围以内,就认为是〝够好〞了。而Shewhart博士观念的目的,是要制程经常稳定一致(Consistency),结果自然是产品尽可能地稳定一致了。因为它们的目的不同,结果也就随之而不同。优思学院认为我们没有必要把这两种观念加以协调。经理人员必须采用其中之一,作为生产制程的指导原则:仅只要求符合规格,还是继续不断地改进制程。
经理人员在工业革命时期就开始采用第一种观念了。大约经过了200年以后,这个目的仍没有达到。因为我们仅仅把目标放在符合规格上,结果却缺乏进步。这就没有理由使人相信将来会有什么进步的缘故。
另一方面,根据日本的经验,应用了Shewhart博士的观念之后,证明了持续不断地改进制程,使得日本的工业产品提高了它们的质量,也提高了它们的生产力。结果,不再局限于以符合规格为满足,而是在持续不断地改进途程中前进。
优思学院认为要产品完全符合规格,唯有持续不断地改进制程,而且仅只有当经理人员用言词和行动来支持这个目标时,才会获得质量和生产力的增加。
收起阅读 »
如果你有看过优思学院关于SPC的六西格玛绿带课程视频,应该会知道在控制界限以内的变异原因,和超出控制界限以外的变异原因两者的区别。这是休哈特(Walter A. Shewhart)博士在 1924年发明第一张质量控制图时,给予的区分,他把两者分别命名为机遇原因(Chance Cause)和非机遇原因(Assignable Cause)。当时的学者为崇敬Shewhart博士把统计学应用在工业上所作的贡献,故亦有称为Shewhart图。
直到1970年,美国的质量管理大师 W. Edwards Deming博士首次应邀访台,在他所发表的学术演讲中,他提出了两个崭新的名词,就是在控制界限以内变异的原因,称为共同原因(Common Cause),超出控制界限以外的变异原因,称为特殊原因(Special Cause)。优思学院看到许多美英等国的质量管理书籍上,也逐渐采用这个名词。尤其近几年来,Deming博士时有新著问世,声望陡增,已成为质量管理界中之牛耳。
我们当时都以为Deming博士把共同原因来代替机遇原因,特殊原因来代替非机遇原因,无非是取其浅显达意,容易明白而已。而且一直以为这两个名词是相等的(即:共同原因 = 机遇原因,特殊原因 = 非机遇原因),没有再去作进一步的研究。
近十年来,美国新出版的质量管理书籍很多,也曾讨论过这些名词的问题,才知道这两个名词并不完全相等,因为Shewhart和Deming两人的出发点,并不一样。兹就读书所得,说明于次。
Shewhart博士的观念是着眼于制程中的变异,凡是在控制下的变异(Controlled Variation),可以认为是稳定(Stable)而经常存在的,所以称之为机遇原因,亦有人称之为无法避免之原因(Unavoidable Cause)者。这种变异是制程中固有的(Inherent)的变异,如果要把它减少(或减小),制程亦必随之而变动。
至于制程中不能控制的变异(Uncontrolled Variation),是随时在变动,既不稳定,亦非经常存在,并不是制程中的一部分。这种不稳定的性质,使制程不能按照预定的目标操作,致产生过多的变异(Excess Variation)。这种变异原因称为非机遇原因,应该可以把这种变异原因找出来,并加以消除掉,使制程回复正常。故这种原因亦有称之为可避免之原因(Avoidable Cause)者。
上述两种方法,都可以用来改进制程,但基本上是不同的。前者是去修改(改善) (Modify)一个经常而稳定的制程,而后者是去创造(Create)一个经常而稳定的制程。到底要采用那一种方法?就要看制程中的变异而定。因此,改进制程的首要步骤,是先要决定制程中有无不能控制的变异原因存在。而Shewhart的质量控制图是根据机率原理和统计学而来的,正是判断制程中有无不能控制的变异原因的有效利器。
至于Deming博士,他的着眼点是放在:谁该对这种变异负责?于是创造了共同原因和特殊原因这两个名词。
共同原因的变异是存在于制造系统(System)或控制良好的系统中。优思学院认为因为这种变异是属于系统内的,所以应该由控制这一系统的人员来负责,那即是:经理人员─特别是高阶层的经理人员。共同原因的变异仅祇能由经理阶层人员采取行动,才能把它移除掉。
特殊原因的变异在本质上是局部的。Deming博士曾说过,他喜欢用〝特殊〞这个形容词来指特定的一群作业员,或特定的某一位作业员,或特定的机器,或特定的局部环境等所造成的特殊原因。他并说,名词并不重要,重要的是观念。一般都能从发生问题的那一特定阶层人员,就可自行找出原因,采取行动,并把困扰的问题消除掉。
这些非机遇原因可以由作业员或那一部分的领班来采取行动。 而共同原因却不然,它可以是机遇原因,也可以是非机遇原因。无论在那一种情况,都是系统上发生的错误(Faults),仅祇能由经理阶层人员采取行动,才能改正过来。 Deming博士是着重在谁该对这种不同型式的变异负责,现在优思学院可以用一句话来说明他的观念:减少任何一个质量特性(如厚度,或绩效等)的变异,不管这个质量特性是否在控制状态之下,甚至只有少数几个或没有不良品产生,都认为是良好的管理。 〝零缺点〞并不能算够好。
工业界必须做到比符合规格还要来得好。经理人员要去研究制程,并且应该去找寻变异的来源,进而把它消除掉,以经常改进产品。质量控制图正是用来找出这些来源的有效利器。当制程中的变异减小后,则零件将更为相似,产品亦将愈佳。这些都是Deming博士在1950年带给日本人的金玉良言,日本人懂得这些话,经过了石川一郎(按:即石川馨氏之尊翁)及小柳贤一等继续不断地努力,才奠定了实施SQC成功的基础。
现在,将再介绍另一个观念(Concept),那就是:工程上(Engineering)对变异的观念,和Shewhart博士(包括Deming博士)对变异的观念,两者完全不同。工程上对变异的观念,其目的是要求产品能符合规格,不管产品中的变异有多大,只要在规格范围以内,就尽可能地让它去变化(Vary)。如果结果是在规格范围以内,就认为是〝够好〞了。而Shewhart博士观念的目的,是要制程经常稳定一致(Consistency),结果自然是产品尽可能地稳定一致了。因为它们的目的不同,结果也就随之而不同。优思学院认为我们没有必要把这两种观念加以协调。经理人员必须采用其中之一,作为生产制程的指导原则:仅只要求符合规格,还是继续不断地改进制程。
经理人员在工业革命时期就开始采用第一种观念了。大约经过了200年以后,这个目的仍没有达到。因为我们仅仅把目标放在符合规格上,结果却缺乏进步。这就没有理由使人相信将来会有什么进步的缘故。
另一方面,根据日本的经验,应用了Shewhart博士的观念之后,证明了持续不断地改进制程,使得日本的工业产品提高了它们的质量,也提高了它们的生产力。结果,不再局限于以符合规格为满足,而是在持续不断地改进途程中前进。
优思学院认为要产品完全符合规格,唯有持续不断地改进制程,而且仅只有当经理人员用言词和行动来支持这个目标时,才会获得质量和生产力的增加。
收起阅读 »
评估质量管理软件/系统(QMS)试金石--试用、试用、还是试用!
近年来,越来越多的企业进行了信息化建设。企业信息化失败,或者至少说是没有完全达到当初的预期,案例比比皆是。
那么,到底如何避免失败?
答:最有效的手段之一就是--试用、试用、还是试用!
为什么要试用?
买双鞋子,你都会穿上试一下,走几步看鞋子是否合脚,穿着是否舒服,是不是硌脚。
企业是如此多种多样,如此千差万别,而且企业为了竞争和生存,还一直处于不断变化之中,不试用一下,怎能知道这个软件是不是适合自己,是不是能够解决企业面临的问题?
很多企业管理者说,那我可以参观一下成功案例。通常是很难看到同行案例(只有为数不多的企业会同意同行参观),即使很幸运看到了同行案例,并且很成功,也无法证明适合别的公司的软件,就一定会适合自己的公司。还是同样的道理,只有自己的脚最知道鞋合适不合适。
在选择工业软件时,“试用”这一火眼金睛术可以帮助企业发现以下潜在问题:
1. 避免被高大上的PPT蒙蔽双眼。
老王卖瓜,自卖自夸。乙方有些吹牛成分可以理解。但有很多软件提供商喜欢语不惊人死不休,还喜欢新造一些词汇来唬人,比如什么人工智能、大数据,什么ERP+MES全方位解决方案,什么万物互联,好像是一个全能的上帝,总之一句话没有他不能做的。对于这样的表演,一些人已经不屑一顾了,但绝大多人还是会被唬住。
这还没完,有些企业把PS本领也搬到了PPT产品介绍上,产品的界面P的非常酷炫;更有甚者,自己的产品没有这个功能,盗取同行的产品界面,放到自己的产品上去,宣称是自己开发的产品。
欺骗客户这事,可别以为只有中国软件企业这样做,美国和德国(美国和德国的工业软件比其它国家多)的软件公司也有这样干的,戳穿这样的把戏很简单,让乙方销售人员用他们的公司的实际软件系统现场展示PPT中出现的界面并走几个流程即可。
2. 现场演示也不一定完全可靠。
软件服务商在客户面前演示,所见即所得,这样该没有问题了吧?魔术也是在你面前表演,但魔术是真实的吗?在短短的展示时间内,客户很难掌握软件系统的全部,也不可能充分理解该系统。再说,乙方会100%毫无保留地展示产品吗?数据的前后逻辑关系是怎么得来的?计算结果对吗?
这里给大家介绍一个小技巧,如果乙方在介绍产品时,不停地在不同系统之间来回切换,你可就要小心了,该乙方的产品很可能不完善,是定制项目型的软件,没有办法在一个系统展示全部功能,所以要在不同系统之间跳来跳去。为什么对项目型产品要小心,道理也是很简单,失败概率大,详细论述可参见《质量管理系统(QMS)-6.自己开发,外包还是购买产品?》。
还有,展示期间甲方不太可能关注到全部细节,但有些细节又十分关键。例如,我们曾经发现多家软件企业(包括市场上一些常见的公司),其质量检验的取样规则违反了国标GB/T 2828.1—2012,系统上线后才发现,这时甲方该怎么办?如果甲方是知名企业且使用了这样低劣的软件,不仅没有对质量做到很好的管控,而且还会对企业商誉造成很大的潜在风险。
3. 验证操作界面是否易于一线员工理解。
如果不易于一线员工理解,实施会遇到很大的阻碍。还有,相对来说,一线员工的离职率比较高,如何让新员工快速掌握,不影响生产,也是一个不容忽视的问题。后期再培训的问题,在项目初期也要有所关注。
4. 乙方介绍的功能适合我们的企业吗?
语言沟通时不免有些歧义,实际测试一下系统便知,避免出现卖家秀和买家秀的问题。
除以上原因,试用还有其它益处吗?
5. 检验乙方软件的成熟度。
乙方在演示的时候,可以躲避一些软件的缺陷,甚至是Bug。 只要甲方在试用时比较细心,这些问题很难被隐藏住。
6. 考察乙方的实施能力。
专业实施能力是软件成功与否的另一个关键要素。甲方在试用时,必然会有一些问题,通过提出问题,就可以看出乙方是否是专业的质量人员,有没有专业服务能力。我们就曾经看到过,有些实施人员完全不懂质量,甲方人员还要花费时间告诉乙方软件公司什么是标准方差,什么是Cpk等专业术语。在这种情况下,还能期望实施过程中乙方给企业的流程带来优化吗?
很多企业购买质量管理软件的初衷包括希望通过实施软件把质量管控流程中不规范的地方一并梳理,如果乙方质量管理不专业,又如何梳理?
7. 让使用部门参与选择。
而不是完全由上级或者IT部门强行塞给使用部门一个系统,以便减少后期使用部门的抱怨和扯皮的事情。
给孩子买鞋子,最好带上孩子。
8. 员工有参与感。
可以根据甲方的实际情况,让多个层级员工参加试用。
9. 避免暗箱操作。
阳光是最好的消毒剂,让大家畅所欲言,把选择放在桌面上。这样选择出的系统,不会让大家失望。
10. 在签合同前,各方达成比较一致的意见。
通常测试是多人测试,给出的反馈更加全面,如果有意见不统一的地方,可以及早提出,避免后期的各种意想不到。
11. 尽量减少开口合同。
一些定制二开有时是不可避免的,但要在签合同时要做到心中有数,要在预算范围之内,如何才能实现呢?在IT部门的帮助下,让实际使用部门给出反馈,是比较接地气的办法。实际使用部门最清楚他们需要什么,什么是雪中送炭,什么是锦上添花,甚至什么是画蛇添足。
(这里的使用部门不能仅仅狭义地理解为质量部门,采购部门可能需要参考供应商质量表现,研发部门可能需要产品问题历史记录,销售和财务可能需要产品直通率来核算产品真实成本,高管可能需要产品质量整改进度表等等,不一而足。)
那么,甲方该如何进行试用?
试用的方法有多种,推荐一个即高效又可检验出乙方专业水平的方法。
第一步:甲方根据自身的需求,可以把相关的脱敏资料(可以公开的数据或者模拟数据)如,来料检验报告、过程检验报告、出货检验报告、客户投诉、评审报告、纠正预防(8D)、不合格品管理流程、以及质量月报等资料发给乙方。
第二步:由乙方搭建一个临时的测试系统,里面的物料号、工序、检验方式都模拟甲方真实运营的情况。
第三步:如果乙方是一个较为完备成熟的系统,可以很快搭建出来一个模拟系统,而不会用其它借口,什么审批之类的来拖延时间。
第四步:甲方按照实际生产和业务处理流程,录入一些实际的检验、不合格品、客诉等数据,不仅可以检验一下乙方的系统是否能够实现企业所需要的数据录入方式、报表分析效果,以及流程是否能够满足要求。还能够快速评估系统对当前需求的匹配程度、以及未来可能存在变化的灵活配置能力,并且可以通过这个模拟系统来进一步考察乙方对甲方的业务理解水平,以及技术支持能力。
第五步:通过测试系统,对于不能满足需求的地方,让乙方给出开发周期以及大致的报价,对项目的整体预算要做到心中有数。
第六步:对乙方的系统,人员专业水平,支持能力,价格等做出综合服务评价,选出合适的系统。
不同于购买一些传统的商品或服务,比如培训或者一个零件,这些都是某种程度上的短暂、小范围合作。购买工业软件就完全不同了,会涉及到多个部门,并且会对企业带来长期影响。不仅仅是系统上线那一时刻的服务很重要,更要考虑到乙方是否能够长期持续地提供基于系统的专业技术服务。选择错了,可能不但帮不到企业,反而成为负担。
收起阅读 »
那么,到底如何避免失败?
答:最有效的手段之一就是--试用、试用、还是试用!
为什么要试用?
买双鞋子,你都会穿上试一下,走几步看鞋子是否合脚,穿着是否舒服,是不是硌脚。
企业是如此多种多样,如此千差万别,而且企业为了竞争和生存,还一直处于不断变化之中,不试用一下,怎能知道这个软件是不是适合自己,是不是能够解决企业面临的问题?
很多企业管理者说,那我可以参观一下成功案例。通常是很难看到同行案例(只有为数不多的企业会同意同行参观),即使很幸运看到了同行案例,并且很成功,也无法证明适合别的公司的软件,就一定会适合自己的公司。还是同样的道理,只有自己的脚最知道鞋合适不合适。
在选择工业软件时,“试用”这一火眼金睛术可以帮助企业发现以下潜在问题:
1. 避免被高大上的PPT蒙蔽双眼。
老王卖瓜,自卖自夸。乙方有些吹牛成分可以理解。但有很多软件提供商喜欢语不惊人死不休,还喜欢新造一些词汇来唬人,比如什么人工智能、大数据,什么ERP+MES全方位解决方案,什么万物互联,好像是一个全能的上帝,总之一句话没有他不能做的。对于这样的表演,一些人已经不屑一顾了,但绝大多人还是会被唬住。
这还没完,有些企业把PS本领也搬到了PPT产品介绍上,产品的界面P的非常酷炫;更有甚者,自己的产品没有这个功能,盗取同行的产品界面,放到自己的产品上去,宣称是自己开发的产品。
欺骗客户这事,可别以为只有中国软件企业这样做,美国和德国(美国和德国的工业软件比其它国家多)的软件公司也有这样干的,戳穿这样的把戏很简单,让乙方销售人员用他们的公司的实际软件系统现场展示PPT中出现的界面并走几个流程即可。
2. 现场演示也不一定完全可靠。
软件服务商在客户面前演示,所见即所得,这样该没有问题了吧?魔术也是在你面前表演,但魔术是真实的吗?在短短的展示时间内,客户很难掌握软件系统的全部,也不可能充分理解该系统。再说,乙方会100%毫无保留地展示产品吗?数据的前后逻辑关系是怎么得来的?计算结果对吗?
这里给大家介绍一个小技巧,如果乙方在介绍产品时,不停地在不同系统之间来回切换,你可就要小心了,该乙方的产品很可能不完善,是定制项目型的软件,没有办法在一个系统展示全部功能,所以要在不同系统之间跳来跳去。为什么对项目型产品要小心,道理也是很简单,失败概率大,详细论述可参见《质量管理系统(QMS)-6.自己开发,外包还是购买产品?》。
还有,展示期间甲方不太可能关注到全部细节,但有些细节又十分关键。例如,我们曾经发现多家软件企业(包括市场上一些常见的公司),其质量检验的取样规则违反了国标GB/T 2828.1—2012,系统上线后才发现,这时甲方该怎么办?如果甲方是知名企业且使用了这样低劣的软件,不仅没有对质量做到很好的管控,而且还会对企业商誉造成很大的潜在风险。
3. 验证操作界面是否易于一线员工理解。
如果不易于一线员工理解,实施会遇到很大的阻碍。还有,相对来说,一线员工的离职率比较高,如何让新员工快速掌握,不影响生产,也是一个不容忽视的问题。后期再培训的问题,在项目初期也要有所关注。
4. 乙方介绍的功能适合我们的企业吗?
语言沟通时不免有些歧义,实际测试一下系统便知,避免出现卖家秀和买家秀的问题。
除以上原因,试用还有其它益处吗?
5. 检验乙方软件的成熟度。
乙方在演示的时候,可以躲避一些软件的缺陷,甚至是Bug。 只要甲方在试用时比较细心,这些问题很难被隐藏住。
6. 考察乙方的实施能力。
专业实施能力是软件成功与否的另一个关键要素。甲方在试用时,必然会有一些问题,通过提出问题,就可以看出乙方是否是专业的质量人员,有没有专业服务能力。我们就曾经看到过,有些实施人员完全不懂质量,甲方人员还要花费时间告诉乙方软件公司什么是标准方差,什么是Cpk等专业术语。在这种情况下,还能期望实施过程中乙方给企业的流程带来优化吗?
很多企业购买质量管理软件的初衷包括希望通过实施软件把质量管控流程中不规范的地方一并梳理,如果乙方质量管理不专业,又如何梳理?
7. 让使用部门参与选择。
而不是完全由上级或者IT部门强行塞给使用部门一个系统,以便减少后期使用部门的抱怨和扯皮的事情。
给孩子买鞋子,最好带上孩子。
8. 员工有参与感。
可以根据甲方的实际情况,让多个层级员工参加试用。
9. 避免暗箱操作。
阳光是最好的消毒剂,让大家畅所欲言,把选择放在桌面上。这样选择出的系统,不会让大家失望。
10. 在签合同前,各方达成比较一致的意见。
通常测试是多人测试,给出的反馈更加全面,如果有意见不统一的地方,可以及早提出,避免后期的各种意想不到。
11. 尽量减少开口合同。
一些定制二开有时是不可避免的,但要在签合同时要做到心中有数,要在预算范围之内,如何才能实现呢?在IT部门的帮助下,让实际使用部门给出反馈,是比较接地气的办法。实际使用部门最清楚他们需要什么,什么是雪中送炭,什么是锦上添花,甚至什么是画蛇添足。
(这里的使用部门不能仅仅狭义地理解为质量部门,采购部门可能需要参考供应商质量表现,研发部门可能需要产品问题历史记录,销售和财务可能需要产品直通率来核算产品真实成本,高管可能需要产品质量整改进度表等等,不一而足。)
那么,甲方该如何进行试用?
试用的方法有多种,推荐一个即高效又可检验出乙方专业水平的方法。
第一步:甲方根据自身的需求,可以把相关的脱敏资料(可以公开的数据或者模拟数据)如,来料检验报告、过程检验报告、出货检验报告、客户投诉、评审报告、纠正预防(8D)、不合格品管理流程、以及质量月报等资料发给乙方。
第二步:由乙方搭建一个临时的测试系统,里面的物料号、工序、检验方式都模拟甲方真实运营的情况。
第三步:如果乙方是一个较为完备成熟的系统,可以很快搭建出来一个模拟系统,而不会用其它借口,什么审批之类的来拖延时间。
第四步:甲方按照实际生产和业务处理流程,录入一些实际的检验、不合格品、客诉等数据,不仅可以检验一下乙方的系统是否能够实现企业所需要的数据录入方式、报表分析效果,以及流程是否能够满足要求。还能够快速评估系统对当前需求的匹配程度、以及未来可能存在变化的灵活配置能力,并且可以通过这个模拟系统来进一步考察乙方对甲方的业务理解水平,以及技术支持能力。
第五步:通过测试系统,对于不能满足需求的地方,让乙方给出开发周期以及大致的报价,对项目的整体预算要做到心中有数。
第六步:对乙方的系统,人员专业水平,支持能力,价格等做出综合服务评价,选出合适的系统。
不同于购买一些传统的商品或服务,比如培训或者一个零件,这些都是某种程度上的短暂、小范围合作。购买工业软件就完全不同了,会涉及到多个部门,并且会对企业带来长期影响。不仅仅是系统上线那一时刻的服务很重要,更要考虑到乙方是否能够长期持续地提供基于系统的专业技术服务。选择错了,可能不但帮不到企业,反而成为负担。
收起阅读 »
为什么会有人质疑SPC?
注:本文初次发表于公众号“质量管理与工具实战交流平台”上。
不久前,流传着一篇题为《质量管理软件(工具)中,SPC真的有用吗?》的微信公众号文章(读者可在微信中的“搜索”查看一下),该文章把SPC批了一个“体无完肤”。其中的观点当然是错误的,业界也相应地出现了一些纠正和澄清的文章。
与直接的纠正做法不同的是,我从另一个角度对这个问题进行了思考:为什么有人会对SPC存在着误解和质疑呢?
事实上人们在学习和使用SPC时存在着大量的误区,尤其是关于SPC的理论基础、准备工作、使用前提、使用前对所控制的过程的初始研究等,这些方面在讲解和学习时被忽视了,只注重了步骤,尤其是把AIAG发布的《SPC参考手册》当作了一种标准条款来解读和使用,这就很难使SPC得到正确的理解和应用,带来的效果就可想而知了,这就会让人误认为SPC是一种没有实用价值的、过时的理论了!
我最近更新了我的SPC课程,着重强调和强化了这些容易被忽视的方面,在本文中限于篇幅,我只是列举其中的一部分控制图中的常见问题。下列方面比较普遍:
第一,缺乏必要的数理统计知识
SPC是基于数理统计理论建立起来的,这就对数理统计基础比较欠缺的人来说,想在有限的时间里理解它的基本原理确实是一个比较严峻的挑战。这些相关的理论至少包括:随机变量、分布、正态、中心极限定理、抽样分布、甚至假设检验等理论讲清楚!只有理解了这些数理统计概念,才能掌握SPC的底层逻辑,才能应对变化万千的制造过程和工作场景,否则,只学习基本的步骤和生硬的规定,接下来所学的SPC就会百无一用了!所以,在讲解和学习SPC的基本知识时,这一块是决不能回避的。
上图中的注释不是具体的失控判断准则,后面还有对每条准则的详细讲解。
第二,SPC的准备工作不充分
1、资源是制约SPC推广应用的重要原因。当前随着制造业自动化、智能化的日益普及,已经越来越多地实现了在线100%或连续检测,一天可能会产生海量的数据,如果还是采用那种几十年前的那种原始的方式,由人工进行数据的采集、上传、分析和报警,效率是很低的,也是不够精确的,好马应当配以好鞍,需要借助于自动SPC系统,必要时与企业的ERP系统相融合,这样才能做到自动、实时、快速地对失控做出反应,减少报警停线带来的损失。
2、与海量数据的情形相反,还有另一种极端的情形,就是感觉没有适合于SPC管控的特性,特别是在一些组装生产线上,或者在一些破坏性测量的工位上。这就需要用一些“前端工序的特性”、“过程特性”使用控制图,或者测量成本较低且与之相关的特性来替代。
3、工作流程上的保障。请问SPC只是质量工程师们的事吗?我们需要一个工作流程上的保证,这样才能够保障SPC能够持续地进行下去。SPC是跨部门的工作,尤其是生产、设备、工艺部门、质量部门共同的职责,需要基于工厂的实际,进行合理的分工与协作。
4、有的人不知道应当在什么时候导入SPC,或者生产过程中尚有一堆问题等待解决时就导入SPC,结果是不能建立起控制限,因为总是存在失控!因此,当过程中还有显而易见的问题未得到解决,还在产生着大量的不合格时,使用控制图是没有任何意义的!
5、我们经常得到下面这样的图形:
很显然,这是测量系统的分辨率不够的缘故,这要结合制造过程本身的变差,如果变差足够小,这就要求测量系统的分辨率更小,至少要做到1/10的过程变差:1/10×6σ。下图是使用不同分辨率的量具测量同一组样件的结果对比:
因此,做好控制图,如果过程是高精度自动化的,测量系统/量具本身就是一个挑战。
第三,缺乏对所控过程的了解
1、不了解数据的分布状态。对于常规控制图来说,在建立控制限时(控制图的分析阶段)是有着一定的前提的(随机、独立、正态),其中要保证图上的点所对应的数据呈现正态分布或者近似正态分布,否则,所建立起来的控制限就会产生假报警或漏报警,就是我们常讲的第一类和第二类错误!
那么这个“近似正态”到底是可以近似到什么程度呢?这是一个容易令人困惑的问题。
有人或有的SPC书籍中认为,先把控制图做出来,如果真的数据不正态,就会通过失控来表现出来(报警),到时候你不就知道了吗?这种说法在正式的在线控制时是正确的,毕竟SPC实质上就是一个大号的假设检验嘛,但是,在建立控制限的分析阶段,是存在着一定的“灰色地带”的,会存在一种“既不是正态,同时又不失控报警”,只是“潜伏”的情形!或者在建立控制限时出现了失控的点,于是去寻找过程中的问题,如果找不到,那么到底是专业知识不够呢,还是本来过程就没问题而是因数据不完全满足正态的条件所生产的假报警呢?难以分辨吧!所以在这样的条件下建立起来的控制限是不够严谨的,仅仅说“近似正态”其实是没有实操价值的!在控制图的分析阶段,我们需要确定的是一个准确的基准-控制限。
因此,我们至少要确保样本的均值之间要呈现正态分布,这就是所说的“原始数据可以近似的程度”衡量依据!
要确保样本均值之间为正态分布,就应当使用正确的样本量,所谓的“小样本、短周期”的抽样方式,只是在原始数据正态的前提下是合理的,如果原始数据不正态,我们应当在确认制造过程当中没有特殊原因的前提下,适当加大样本量,以使得均值之间为正态分布(依据中心极限定理),或者通过其他的手段,如非正态向正态的转化、寻求个体分布的参数、非参数等,而不是生搬硬套、千篇一律地使用同一种控制图(如均值-极差图)。看来这也是SPC“曲高和寡”的原因之一吧,因为它确实需要使用者具有较高的数理统计功底的。
2、不了解所控制过程的特定失控模式。我经常听到过这样的反馈:导入SPC后失控报警了总是找不到原因,太影响生产了,后来我们就干脆又把SPC撤掉了。这是多么遗憾的一件事啊!
这是什么原因呢?其中的原因有:建立控制限时所用样本不能代表和包含实际过程的变差,使均值图的控制限过窄,盲目使用那常用的8个判异准则、缺乏事前对过程失效模式的分析(与PFMEA的对接)等。对于一个特定的加工过程,我们用控制图来控制的特性应当会从PFMEA中找到相应的失效模式及失效起因,即使没有做PFMEA,我们也应当事先来分析和识别出一些发生频度较高的失效起因,评估这些起因如果存在,会在控制图上引起哪种类型的失控模式,从而确定我们要采用哪几个判异准则(超控制限这个是必须使用的)。这样把工作做到前头,一旦将来出现失控报警,就会沿寻着事先的分析路径,快速把失控搞定,使过程恢复受控状态。
例如,气动夹紧工装,可能会出现气体管路漏气或螺丝松动的问题,如果使用控制图对夹紧力进行监控,那么可能会出现下列失控模式:
因为一旦气体发生泄漏或螺丝产生松动,其程度就会快速地恶化,反应在夹紧力上就是逐渐下降的趋势。在对夹紧力使用控制图控制之前,就应当先将这些可能的因素和由此引起的失控模式识别出来和确定下来。
再如,当加工的基准面的定位不正确时,就会出现下面这样的失控模式:
那么你的过程存在基准面变动的因素吗?
3、对抽样的时机制定太死板。对于一个过程,人员/班次、原材批次的更迭,还有设备的重启、重设等都是产生显著变差(特殊原因)的机会,如果只是机械地等时间间隔来抽样,就会错过这些变差机会,所以还需要基于所控过程的要素(4M1E)水平更的迭来有针对性地抽样,以便及时捕捉变差和可能的特殊原因。
第四、出现失控后不明确如何反应
大家都在注重如何制作控制图,如何判断失控,却没有一个明确的规则来说明出现失控后如何反应。在AIAG的SPC参考手册中也没有明确的规定。
对于不同的失控模式,我们需要做出不同的反应,这包括下列选项:分析原因、停止生产、隔离产品。在我的课程中进行了讲述。例如,对于下列失控模式,我们应当停止生产、隔离产品:
再就是,产品被隔离后再怎么做呢?在上述情况中,应当是进行PPK(注意这时不应当是CPK了)的研究,看是否已经低于了PPK目标值了,如果是,就应当按照与客户的约定进行处置(发货前全检或者追加抽检等)。
而对于下列情况,只需要分析原因:
还有一个需要澄清的问题,就是“失控ARL”(平均运行长度)。当均值图上有点发生失控后,在所发生的点上看不到这个失控,直到再抽若干次样后才在图上表现出来,这样的平均抽样次数为失控ARL。在AIAG的SPC参考手册中,只是提到了“受控ARL”,即两次假失控报警之间的平均运行长度(抽样次数)。
在控制图的实际运用过程中,失控ARL是相当重要的,如果没有这个概念,当失控时,就不能隔离出所有的可能受到影响的产品。
第五、控制图长期不更新
虽然在分析阶段建立的控制限是在线使用阶段的控制基准,一般不能进行更改,但是在下列情况下,应当适时更新:
过程进行持续改善后,或者增加了过程的防错后,应当重新计算控制限,否则就会失去应有的灵敏度。在所控特性的目标值发生变更时,也应当重新设置控制限,因为目标值变了,相应的加工基准也要做出改变,过程的均值也会发生改变,若还是保持现有的控制限,就会出出均值偏移的“失控”。
限于篇幅,就写到这里吧,其实我的更新版的SPC课程中还有更多的与众不同的亮点的。
收起阅读 »
不久前,流传着一篇题为《质量管理软件(工具)中,SPC真的有用吗?》的微信公众号文章(读者可在微信中的“搜索”查看一下),该文章把SPC批了一个“体无完肤”。其中的观点当然是错误的,业界也相应地出现了一些纠正和澄清的文章。
与直接的纠正做法不同的是,我从另一个角度对这个问题进行了思考:为什么有人会对SPC存在着误解和质疑呢?
事实上人们在学习和使用SPC时存在着大量的误区,尤其是关于SPC的理论基础、准备工作、使用前提、使用前对所控制的过程的初始研究等,这些方面在讲解和学习时被忽视了,只注重了步骤,尤其是把AIAG发布的《SPC参考手册》当作了一种标准条款来解读和使用,这就很难使SPC得到正确的理解和应用,带来的效果就可想而知了,这就会让人误认为SPC是一种没有实用价值的、过时的理论了!
我最近更新了我的SPC课程,着重强调和强化了这些容易被忽视的方面,在本文中限于篇幅,我只是列举其中的一部分控制图中的常见问题。下列方面比较普遍:
第一,缺乏必要的数理统计知识
SPC是基于数理统计理论建立起来的,这就对数理统计基础比较欠缺的人来说,想在有限的时间里理解它的基本原理确实是一个比较严峻的挑战。这些相关的理论至少包括:随机变量、分布、正态、中心极限定理、抽样分布、甚至假设检验等理论讲清楚!只有理解了这些数理统计概念,才能掌握SPC的底层逻辑,才能应对变化万千的制造过程和工作场景,否则,只学习基本的步骤和生硬的规定,接下来所学的SPC就会百无一用了!所以,在讲解和学习SPC的基本知识时,这一块是决不能回避的。
上图中的注释不是具体的失控判断准则,后面还有对每条准则的详细讲解。
第二,SPC的准备工作不充分
1、资源是制约SPC推广应用的重要原因。当前随着制造业自动化、智能化的日益普及,已经越来越多地实现了在线100%或连续检测,一天可能会产生海量的数据,如果还是采用那种几十年前的那种原始的方式,由人工进行数据的采集、上传、分析和报警,效率是很低的,也是不够精确的,好马应当配以好鞍,需要借助于自动SPC系统,必要时与企业的ERP系统相融合,这样才能做到自动、实时、快速地对失控做出反应,减少报警停线带来的损失。
2、与海量数据的情形相反,还有另一种极端的情形,就是感觉没有适合于SPC管控的特性,特别是在一些组装生产线上,或者在一些破坏性测量的工位上。这就需要用一些“前端工序的特性”、“过程特性”使用控制图,或者测量成本较低且与之相关的特性来替代。
3、工作流程上的保障。请问SPC只是质量工程师们的事吗?我们需要一个工作流程上的保证,这样才能够保障SPC能够持续地进行下去。SPC是跨部门的工作,尤其是生产、设备、工艺部门、质量部门共同的职责,需要基于工厂的实际,进行合理的分工与协作。
4、有的人不知道应当在什么时候导入SPC,或者生产过程中尚有一堆问题等待解决时就导入SPC,结果是不能建立起控制限,因为总是存在失控!因此,当过程中还有显而易见的问题未得到解决,还在产生着大量的不合格时,使用控制图是没有任何意义的!
5、我们经常得到下面这样的图形:
很显然,这是测量系统的分辨率不够的缘故,这要结合制造过程本身的变差,如果变差足够小,这就要求测量系统的分辨率更小,至少要做到1/10的过程变差:1/10×6σ。下图是使用不同分辨率的量具测量同一组样件的结果对比:
因此,做好控制图,如果过程是高精度自动化的,测量系统/量具本身就是一个挑战。
第三,缺乏对所控过程的了解
1、不了解数据的分布状态。对于常规控制图来说,在建立控制限时(控制图的分析阶段)是有着一定的前提的(随机、独立、正态),其中要保证图上的点所对应的数据呈现正态分布或者近似正态分布,否则,所建立起来的控制限就会产生假报警或漏报警,就是我们常讲的第一类和第二类错误!
那么这个“近似正态”到底是可以近似到什么程度呢?这是一个容易令人困惑的问题。
有人或有的SPC书籍中认为,先把控制图做出来,如果真的数据不正态,就会通过失控来表现出来(报警),到时候你不就知道了吗?这种说法在正式的在线控制时是正确的,毕竟SPC实质上就是一个大号的假设检验嘛,但是,在建立控制限的分析阶段,是存在着一定的“灰色地带”的,会存在一种“既不是正态,同时又不失控报警”,只是“潜伏”的情形!或者在建立控制限时出现了失控的点,于是去寻找过程中的问题,如果找不到,那么到底是专业知识不够呢,还是本来过程就没问题而是因数据不完全满足正态的条件所生产的假报警呢?难以分辨吧!所以在这样的条件下建立起来的控制限是不够严谨的,仅仅说“近似正态”其实是没有实操价值的!在控制图的分析阶段,我们需要确定的是一个准确的基准-控制限。
因此,我们至少要确保样本的均值之间要呈现正态分布,这就是所说的“原始数据可以近似的程度”衡量依据!
要确保样本均值之间为正态分布,就应当使用正确的样本量,所谓的“小样本、短周期”的抽样方式,只是在原始数据正态的前提下是合理的,如果原始数据不正态,我们应当在确认制造过程当中没有特殊原因的前提下,适当加大样本量,以使得均值之间为正态分布(依据中心极限定理),或者通过其他的手段,如非正态向正态的转化、寻求个体分布的参数、非参数等,而不是生搬硬套、千篇一律地使用同一种控制图(如均值-极差图)。看来这也是SPC“曲高和寡”的原因之一吧,因为它确实需要使用者具有较高的数理统计功底的。
2、不了解所控制过程的特定失控模式。我经常听到过这样的反馈:导入SPC后失控报警了总是找不到原因,太影响生产了,后来我们就干脆又把SPC撤掉了。这是多么遗憾的一件事啊!
这是什么原因呢?其中的原因有:建立控制限时所用样本不能代表和包含实际过程的变差,使均值图的控制限过窄,盲目使用那常用的8个判异准则、缺乏事前对过程失效模式的分析(与PFMEA的对接)等。对于一个特定的加工过程,我们用控制图来控制的特性应当会从PFMEA中找到相应的失效模式及失效起因,即使没有做PFMEA,我们也应当事先来分析和识别出一些发生频度较高的失效起因,评估这些起因如果存在,会在控制图上引起哪种类型的失控模式,从而确定我们要采用哪几个判异准则(超控制限这个是必须使用的)。这样把工作做到前头,一旦将来出现失控报警,就会沿寻着事先的分析路径,快速把失控搞定,使过程恢复受控状态。
例如,气动夹紧工装,可能会出现气体管路漏气或螺丝松动的问题,如果使用控制图对夹紧力进行监控,那么可能会出现下列失控模式:
因为一旦气体发生泄漏或螺丝产生松动,其程度就会快速地恶化,反应在夹紧力上就是逐渐下降的趋势。在对夹紧力使用控制图控制之前,就应当先将这些可能的因素和由此引起的失控模式识别出来和确定下来。
再如,当加工的基准面的定位不正确时,就会出现下面这样的失控模式:
那么你的过程存在基准面变动的因素吗?
3、对抽样的时机制定太死板。对于一个过程,人员/班次、原材批次的更迭,还有设备的重启、重设等都是产生显著变差(特殊原因)的机会,如果只是机械地等时间间隔来抽样,就会错过这些变差机会,所以还需要基于所控过程的要素(4M1E)水平更的迭来有针对性地抽样,以便及时捕捉变差和可能的特殊原因。
第四、出现失控后不明确如何反应
大家都在注重如何制作控制图,如何判断失控,却没有一个明确的规则来说明出现失控后如何反应。在AIAG的SPC参考手册中也没有明确的规定。
对于不同的失控模式,我们需要做出不同的反应,这包括下列选项:分析原因、停止生产、隔离产品。在我的课程中进行了讲述。例如,对于下列失控模式,我们应当停止生产、隔离产品:
再就是,产品被隔离后再怎么做呢?在上述情况中,应当是进行PPK(注意这时不应当是CPK了)的研究,看是否已经低于了PPK目标值了,如果是,就应当按照与客户的约定进行处置(发货前全检或者追加抽检等)。
而对于下列情况,只需要分析原因:
还有一个需要澄清的问题,就是“失控ARL”(平均运行长度)。当均值图上有点发生失控后,在所发生的点上看不到这个失控,直到再抽若干次样后才在图上表现出来,这样的平均抽样次数为失控ARL。在AIAG的SPC参考手册中,只是提到了“受控ARL”,即两次假失控报警之间的平均运行长度(抽样次数)。
在控制图的实际运用过程中,失控ARL是相当重要的,如果没有这个概念,当失控时,就不能隔离出所有的可能受到影响的产品。
第五、控制图长期不更新
虽然在分析阶段建立的控制限是在线使用阶段的控制基准,一般不能进行更改,但是在下列情况下,应当适时更新:
过程进行持续改善后,或者增加了过程的防错后,应当重新计算控制限,否则就会失去应有的灵敏度。在所控特性的目标值发生变更时,也应当重新设置控制限,因为目标值变了,相应的加工基准也要做出改变,过程的均值也会发生改变,若还是保持现有的控制限,就会出出均值偏移的“失控”。
限于篇幅,就写到这里吧,其实我的更新版的SPC课程中还有更多的与众不同的亮点的。
收起阅读 »
优思学院:Weibull 分布 和 Lognormal 分布 (一)
原刊于优思学院知乎帐号
无论是质量工程师、六西格玛绿带、六西格玛黑带,他们一般都对正态分布相当熟悉和了解。始终,正态分布是最常见的概率分布,不过当他们遇到非正态的分布时往往无所适从,如果他们忘记了验证这些分布,甚至会错误地预设了那些非正态的分布为正态。
今天,优思学院希望介绍两个概率分布,这两个概率分布虽然知道的人不多,但其实应用非常广泛,它们就是----Weibull 分布 和 Lognormal 分布。这两种非正态分布在服务业中颇为常见。
还记得这张图吗?这是总体与样本,我们在总体取出N个样本,然后便可以从中计算出均值和标准差之类的估算值,以描述样本中的观察结果。在统计数据中,直方图通常表示样本,而曲线通常代表整个总体。
首先,我们先重温一下何谓正态分布。正态分布的机率的函数曲线是对称的,看起来有点像钟形,因此人们又经常称之为钟形曲线(类似于寺庙里的大钟,因此而得名)。
让我们用一个例子来说明。我测试了咖啡因在咖啡豆(样本数量N为 50)中的含量百分比,并找到一个像这样的直方图。我还发现平均值为0.078。且标准差为0.020。
优思学院・六西格玛
您可以看到数据看起来有点像钟形,和它围绕均值对称。直方图中的蓝色条显示测量样品中50个值的分布。红色曲线是预测的总体,当样本数量只有50,您需要一些想像力去识别正态分布。
当然,如果样本数量N增大的话,直方图会开始看起来更像钟形。就像以下这些图表所见的情况,我们可以确定它可以作为正态分布来使用。
优思学院・六西格玛
现在,让我们看另一个例子。
我们收集了各个银行处理索赔的处理时间(Throughput time)的次数。这是一个直方图,指的是我们的每次的处理时间,较集中于0-30之间。然后,我们可以拟合正态分布曲线(红线),就好像下图一样,你觉得合适吗?
优思学院・六西格玛
很明显,答案是否定的。
因为,直方图和正态分布曲线明显呈不同的形状,直方图中也不能看到它围绕均值对称,假如,我们用红线作为依据,而不理会直方图的话,便会误以为只有一半的索赔处理时间在30分钟以下,然而,事实上从直方图所见却非如此。因此,我们可以说这个数据并不符合正态分布。
幸运的是,在这种情况下,我们还有以下两种分布是有可能合适的分布。
第一种,是Weibull分佈,它是一种偏态分布。就是分布是偏向一側,是它的尾巴位于另一侧。Weibull分佈通常用于数据,例如吞吐量时间和处理时间等,因为这些通常是偏斜的变量,它看起来像这样:优思学院・六西格玛・Weibull分佈
第二种,是Lognormal分布,同样常用于偏斜数据,中文译作对数正态分布。它看起来像这样:优思学院・六西格玛・Lognormal分布
从图形形状看来,两种分布都应该比正态分布更适合用于我们关于银行索赔的处理时间这个例子上。
今天先谈到这里,我们会在下一篇进一步说明应该如何利用Minitab选择适合的概率分布。 收起阅读 »
无论是质量工程师、六西格玛绿带、六西格玛黑带,他们一般都对正态分布相当熟悉和了解。始终,正态分布是最常见的概率分布,不过当他们遇到非正态的分布时往往无所适从,如果他们忘记了验证这些分布,甚至会错误地预设了那些非正态的分布为正态。
今天,优思学院希望介绍两个概率分布,这两个概率分布虽然知道的人不多,但其实应用非常广泛,它们就是----Weibull 分布 和 Lognormal 分布。这两种非正态分布在服务业中颇为常见。
还记得这张图吗?这是总体与样本,我们在总体取出N个样本,然后便可以从中计算出均值和标准差之类的估算值,以描述样本中的观察结果。在统计数据中,直方图通常表示样本,而曲线通常代表整个总体。
首先,我们先重温一下何谓正态分布。正态分布的机率的函数曲线是对称的,看起来有点像钟形,因此人们又经常称之为钟形曲线(类似于寺庙里的大钟,因此而得名)。
让我们用一个例子来说明。我测试了咖啡因在咖啡豆(样本数量N为 50)中的含量百分比,并找到一个像这样的直方图。我还发现平均值为0.078。且标准差为0.020。
优思学院・六西格玛
您可以看到数据看起来有点像钟形,和它围绕均值对称。直方图中的蓝色条显示测量样品中50个值的分布。红色曲线是预测的总体,当样本数量只有50,您需要一些想像力去识别正态分布。
当然,如果样本数量N增大的话,直方图会开始看起来更像钟形。就像以下这些图表所见的情况,我们可以确定它可以作为正态分布来使用。
优思学院・六西格玛
现在,让我们看另一个例子。
我们收集了各个银行处理索赔的处理时间(Throughput time)的次数。这是一个直方图,指的是我们的每次的处理时间,较集中于0-30之间。然后,我们可以拟合正态分布曲线(红线),就好像下图一样,你觉得合适吗?
优思学院・六西格玛
很明显,答案是否定的。
因为,直方图和正态分布曲线明显呈不同的形状,直方图中也不能看到它围绕均值对称,假如,我们用红线作为依据,而不理会直方图的话,便会误以为只有一半的索赔处理时间在30分钟以下,然而,事实上从直方图所见却非如此。因此,我们可以说这个数据并不符合正态分布。
幸运的是,在这种情况下,我们还有以下两种分布是有可能合适的分布。
第一种,是Weibull分佈,它是一种偏态分布。就是分布是偏向一側,是它的尾巴位于另一侧。Weibull分佈通常用于数据,例如吞吐量时间和处理时间等,因为这些通常是偏斜的变量,它看起来像这样:优思学院・六西格玛・Weibull分佈
第二种,是Lognormal分布,同样常用于偏斜数据,中文译作对数正态分布。它看起来像这样:优思学院・六西格玛・Lognormal分布
从图形形状看来,两种分布都应该比正态分布更适合用于我们关于银行索赔的处理时间这个例子上。
今天先谈到这里,我们会在下一篇进一步说明应该如何利用Minitab选择适合的概率分布。 收起阅读 »