相关与回归分析知识点小结

相关与回归分析
13.1 理解相关关系与确定性关系
相关关系：通过相关系数的定量研究，确定两者是否相关
确定性关系：Y=F(x)，已有一定的函数关系
13.2 相关系数的概念
相关系数r(也称Pearson)是用来描述两个变量相关程度的一种度量。
-1≤r≤1，当r=±1时，表明n个点全在一条直线上，这时两个变量间完全线性相关；
当r=0时，称两个变量不线性相关，此时散点图上n个点可能毫无规律，也可能两个变量间有某种曲线的趋势；
当r>0时，称两个变量间具有正相关；
当r<0时，称两个变量间具有负相关
13.3 回归分析的前提条件在MINITAB中实现
回归分析是在查找因变量与自变量之间的函数关系。它是一种对于一批有两个或多个变量独立观测数据点的分析方法。
使用回归分析的前提条件是已经确认因变量与自变量是有关联的，具有一定的函数关系（如线性）。这步我们通常用散点图来实现。通过散点图，来看数据是否有正相关或负相关性，有没有特殊点，数据是否有周期性。
散点图：Graph----Scatterplot
13.4 计算机输出结果的理解
首先看回归方程是否显著，我们建立回归方程的目的是去表达两个具有线性相关的变量间的定量关系，因此，只有当两个变量确实具有线性相关时所建立的回归方程才是有意义的。
13.5 REGRESSION与FITTED LINE PLOT的区别
REGRESSION：自变量Y为一个，因变量X可以为一个或多个。建立的是多元回归方程。
FITTED LINE PLOT：自变量Y为一个，因变量X为一个，建立的是一元多次(一次、二次、三次)回归方程。
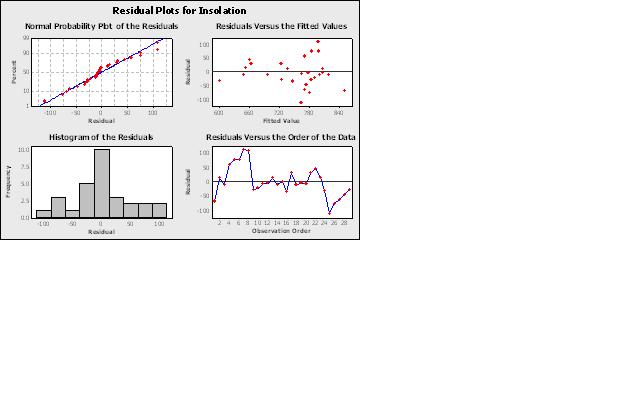
13.6 残差诊断
图片见附件1
左上角：残差的正态性检验图，在本图中未看到任何不正常，如果对正态性有怀疑，可以直接对残差数据进行正态性检验；
左下角：残差直方图；
右上角：关于因变量y的预测值的残差图。因为我们假定残差的标准差是个常数，它不随预测值而变化，因此，这个残差图上的点应该分布在一个水平的带子中。如果在图中有明显的“喇叭口”的形状，即表明残差的标准差不是常数，而是随预测值变化而变化的，如果出现这种情况，可以通过对y做变换加以解决。
右下角：关于按观测顺序的残差图，关于按观测顺序的残差图是用水平轴表示观测顺序，用纵轴表示对应的残差值。这些残差点应在横轴(即残差为0)上下随机波动着，不应有任何上升、下降、摆动、跳跃等趋势。如果有某种趋势存在，则说明数据观测过程中受到某个未知因素的强大影响，应找出此因素并加以控制。
图片见附件2
关于自变量x的值的残差图：水平轴为自变量，纵轴表示对应的残差值。对于此图分析的重点是看残差的标准差是否能保持常数(即各残差点是否有“喇叭口”)或是否有弯曲的形状。如果对y的预报值的残差图也不正常，首先要考虑对y做变换；而如果对y的预报值的残差图正常，这时说明在回归方程中仅有线性项不够，要增加x的高阶项或其他项。
12.7 MINITAB实现回归方程的点预测与区间预测
详见＜回归分析＞第13页。
13.8 如何将非线性回归方程通过转化实现线性回归
对x或y进行变换，转化为线性回归。根据专业知识或数据的散点图分布，找到合适函数变换。
13.9 通过什么指标选择最佳回归方程
图片见附件3
相关指数R愈大愈好；
残差标准差s愈小愈好。
先看残差标准差s，再看相关指数R。如果s比较接近，则R愈大愈好。
13.10 对多元回归方程如何确定关键影响因子
在回归方程显著的前提下，看各因子的P值，如果＜α，由说明该因子显著。
13.11 如何实现回归方程的优化
当我们得到的回归方程是显著的，并且每一个系数也都是显著的，那么回归方程可用于预测。
当有不显著的系数时，一次只能删除一个F值最小的变量，重新计算回归系数，再重新检验。一般要到所有的系数为显著时为止。