关于方差分析的一道实际案例分析及思考

手上有个项目，是服务业关于缩短排队等候时间的一个项目。想分析下排队人数与每周7天之间是否有显著性差异。分析过程如下
1、收集了近半年的历史数据，整理后如下：
星期 排队人员数量
3 133
4 141
5 174
6 131
7 135
1 55
2 62
3 41
4 71
5 92
6 61
7 42
1 180
2 175
3 160
4 127
5 152
6 77
7 43
1 168
2 130
3 134
4 141
5 170
6 89
7 48
1 172
2 202
3 160
4 124
5 150
6 71
7 58
1 177
2 176
3 111
4 136
5 172
6 66
7 53
1 163
2 170
3 155
4 144
5 169
6 79
7 67
1 229
2 179
3 184
4 145
5 168
6 70
7 43
1 228
2 172
3 151
4 150
5 178
6 76
7 47
1 164
2 180
3 144
4 161
5 163
6 84
7 43
1 196
2 163
3 135
4 145
5 136
6 71
7 47
1 172
2 168
3 156
4 142
5 138
6 76
7 42
1 187
2 163
3 162
4 168
5 141
6 87
7 41
1 175
2 171
3 157
4 145
5 182
6 181
7 47
1 60
2 43
3 148
4 163
5 169
6 81
7 52
1 182
2 158
3 126
4 172
5 145
6 68
7 46
1 172
2 143
3 133
4 153
5 138
6 62
7 58
1 161
2 145
3 111
4 141
5 119
6 54
7 30
1 132
2 140
3 112
4 115
5 140
6 115
7 112
1 147
2 88
3 36
4 22
5 62
6 43
7 30
1 56
2 59
3 153
4 174
5 175
6 66
7 47
1 208
2 176
3 155
4 119
5 147
6 74
7 47
1 162
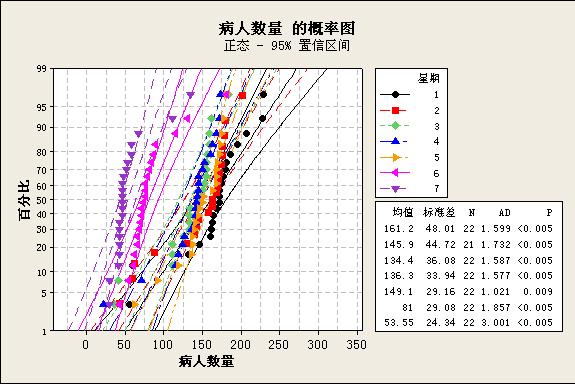
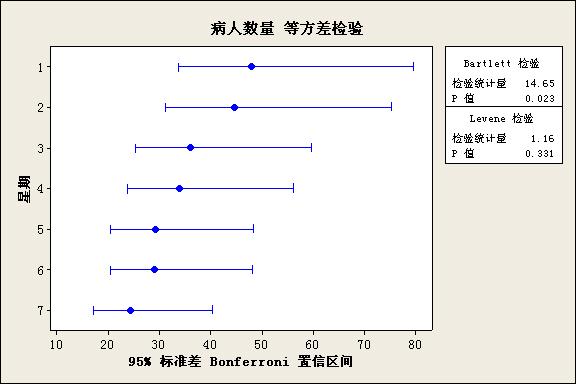
2、分析方法采用的单因子方差分析。先进行正态性检验及方差齐次性检验，结果如下：


从上面来看，数据不是正态的，根据Levene检验结果P＝0.331，可接受星期几之间数据方差是齐次的。
_单因子方差分析: 数量 与 星期

来源 自由度 SS MS F P
星期 6 209720 34953 27.14 0.000
误差 146 187999 1288
合计 152 397719

S = 35.88 R-Sq = 52.73% R-Sq（调整） = 50.79%


平均值（基于合并标准差）的单组 95% 置信区间
水平 N 平均值 标准差 ---------+---------+---------+---------+
1 22 161.18 48.01 (---*---)
2 21 145.86 44.72 (----*---)
3 22 134.41 36.08 (---*----)
4 22 136.32 33.94 (---*---)
5 22 149.09 29.16 (----*---)
6 22 81.00 29.08 (---*---)
7 22 53.55 24.34 (---*----)
---------+---------+---------+---------+
70 105 140 175

合并标准差 = 35.88_
结论：从R－sq值，可认为模型是可接受的，从p值可认为不同星期几对数量有显著性差异。周六、周日的人员明显比周一到周五的人员少。

分析过程就是这样，但我在分析时突然想到个问题就是，方差分析的前提是假设数据来源于正态总体，且方差是相同的。但实际在进行分析时，许多数据都不是正态的、齐次的。在本例中，数据不是正态的，但正好Levene检验出结果是齐次的，如果说数据又不是正态又不是齐次的，哪能进行方差分析吗？遇上这种情况应该怎么下手呢？特别是多因子的方差分析？

抛砖引玉，请大家多多顶下！