正态概率图中95%置信区间
正态概率图中的95%置信区间是逐点计算的,但是在各种资料里都没有找到置信区间的算法;
还请各位大侠指教。。
举最简单的例子:
1 1 2 2 3 3 4 4 5 5 6 6 7 7
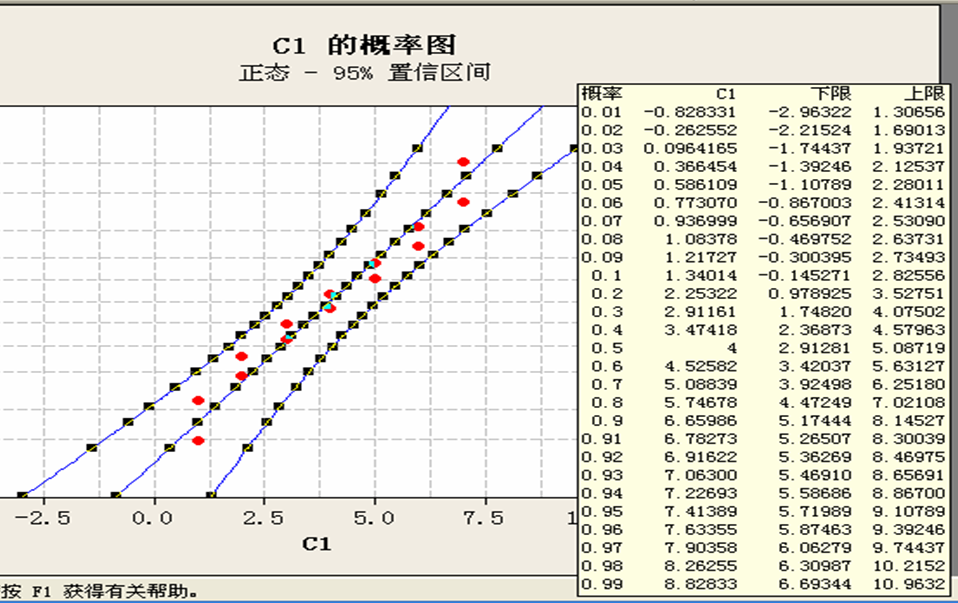
绘制正态概率图:
其中:
概率值 拟合值 下限 上限
0.1 1.34014 -0.145271 2.82556
0.2 2.25322 0.978925 3.52751
0.5 4 2.91281 5.08719
问题:逐点计算置信区间,各点处sigma的计算方法?
为什么当概率值为0.5时,置信区间范围最窄——拟合效果好?
还请各位大侠指教。。
举最简单的例子:
1 1 2 2 3 3 4 4 5 5 6 6 7 7
绘制正态概率图:
其中:
概率值 拟合值 下限 上限
0.1 1.34014 -0.145271 2.82556
0.2 2.25322 0.978925 3.52751
0.5 4 2.91281 5.08719
问题:逐点计算置信区间,各点处sigma的计算方法?
为什么当概率值为0.5时,置信区间范围最窄——拟合效果好?
没有找到相关结果
已邀请:





3 个回复
ophylia (威望:1) (广东 广州) 在校学生 经理 - 习百家真言,悟变化之道
赞同来自:
正态概率图是一个散点图,其中一条轴是排列后的数据值,另外一条轴时他们相应于标准正态分布的期望Z值,可以将数据看作输入数据和输出响应,建立简单的一元线性回归,
其均值的置信区间为
Yp-+ T(a/2)S (y)
S(y)=sXsqrt{1/n+^2/sum(xi-mean(x))^2}
公式写的不好看,你查查书上,由此计算出来的置信区间,因越靠近中心位置,S(y)越小,故中心位置置信区间线窄,如果看不明白给我留言,我下次帮你写详细点,吃饭去了