控制线过窄——SPC中实行中遇到的实际问题?
本帖最后由 wangyuncg 于 2010-9-5 23:12 编辑
求助各位:
我在SPC中实行中遇到了一个实际问题。
就是根据125个数据先做分析用控制图以确定控制线时,导入数据后minitab生成的UCL LCL间距只有0.004,太窄了!
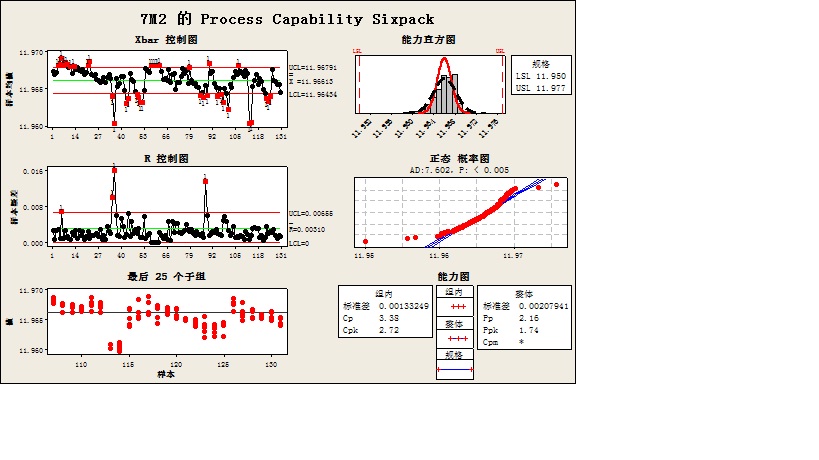
即UCL=11.96791、X =11.96613、LCL=11.96434 (公差带是0.027,用的加工中心)
过程能力还不错,但因为控制线太窄,造成了我Xbar-R图里面很多点都超界了。如图
那么在实际应用中不是很容易就超界了吗?具体该怎么操作控制啊?
求助各位:
我在SPC中实行中遇到了一个实际问题。
就是根据125个数据先做分析用控制图以确定控制线时,导入数据后minitab生成的UCL LCL间距只有0.004,太窄了!
即UCL=11.96791、X =11.96613、LCL=11.96434 (公差带是0.027,用的加工中心)
过程能力还不错,但因为控制线太窄,造成了我Xbar-R图里面很多点都超界了。如图
那么在实际应用中不是很容易就超界了吗?具体该怎么操作控制啊?
没有找到相关结果
已邀请:





29 个回复
rfmd (威望:0) (北京 ) 电子制造 员工
赞同来自: 岚_537
这个情况我想是很多公司都会遇到的
问题出在sigma的计算上
我们都说Xbar+/-3sigma或是Cpk时也说Sigma
但这两个Sigma与Ppk中的Sigma计算方法是不同的
为什么呢?
因为按照经典SPC及six sigma的原则
当你过程稳定以后
应该是特殊原因基本消除或很少,过程的波动主要表现为普通原因
此时我们用控制图去侦测特殊原因,也就是异常
这个时候过程的整体变异与普通原因引起的变异应该是非常接近的
此时Xbar-R或其他类型的控制图才能真实地起到作用
为你的过程侦测异常波动
但是你这个过程不是这样(说是在的很多公司跟你的情况一样)
因为你的过程波动主要表现在特殊原因引起的波动,而不是普通原因引起的波动
就是说普通原因引起的波动很小,因此你的控制线很窄,并且Cpk也很大
因为控制线与Cpk里的sigma只有普通原因的变异,而Ppk里的Sigma是总变异
由于Ppk与Cpk中的sigma算法不同,因此Cpk与Ppk差别较大
如果是统计意义上的稳定过程的话,Cpk与Ppk计算结果应该差不多才对,Ppk略小
这样讲你应该能明白为什么你的异常点这么多了吧
再多说些
你没发现你的过程是一个典型的批内差异小,批与批之间差异大的过程吗?
这样的过程,你现在要做的是,找到批与批之间差异大的原因
我估计,原因有这几种可能
可能你抽样时,单批次已经人为选定了差异比较小的样本,这种情况你可以重新审查一下怎么取样才能代表过程的真实水平
或者是这个大差异来自于设备或原材料,或前工序等等,你几乎无法控制
这个时候你或者想办法改进你的变异来源,或者对变异来源进行分类
相近的变异来源绘制一张控制图
这两种情况你按照传统的Xbar-R的原则来使用就是错误的,而且只会自寻烦恼
如果我说的以上2点你都做不了或不能做的话
你这样情况可以不按照传统的控制线计算方法
可以使用公差线内缩的方式来制定
具体办法不一,有的是控制范围是公差范围的2/3,有的是1/2,还有3/4
其实没有什么标准了
正确的内缩方法是依据你的过程可调整情况来定
如果你的过程出现异常,你可以很轻松或不花费成本不影响生产的情况下来进行调整
这个时候你可以把控制线定的稍微窄一点
如果出现异常时,你去调整过程时比较困难或不经济
此时你可以把控制先定的稍微宽一点
这两种情况下你需要谨慎去判断
谨防:1、有问题侦测不到,或2、没问题或判断为异常而过度调整
具体方法你可以具体去琢磨,说白了就是“控制”与“成本”的平衡
我说的不见得很清楚
但是你要保证的的Cpk/Ppk不会随时间而降低