直方图分析中关于正常型与平顶型的区分

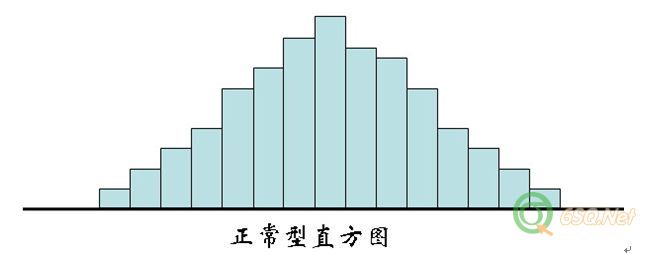
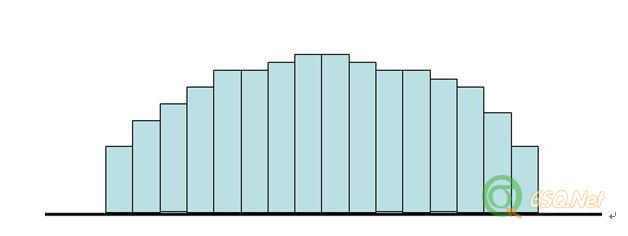
在直方图分析时将有一顶峰左右基本对称的图形属于正常型（如第一张图那样），因为他在统计上大致服从正态分布，似乎很合理，毋庸置疑。但对于平顶型，我感觉似乎没那么简单，特别是像第二幅图那样的平顶（暂且按现在大多数人的分法将其定为平顶型），因为在QC管理中我们的对产品的要求是尽量使其性能指标靠近期望值以使质量损失最小，而这样的数据出现如果他们又都在控制线之内并且不偏向分布的话就完全符合控制目的了，那么我们还是否应该将其判定为平顶型呢？想和大家探讨一下

在此我先说一下个人想法：
第一，他不该归为平顶型（如果会出现这种统计数据的话），因为他可以说完美符合要求。他的出现我认为原因可能是：1、数据精度不够，如果将其放大就会显现出其其它的形状（正常型）。2分组不当，但总体控制比较好使总体数据向内集中。
第二，除了上述原因这种情况不会出现，因为他不符合正态分布，正常的平顶型应该类似锯齿或偏向型的
但我更大程度上相信这种情况在质量统计过程中是不会出现的:lol: