Minitab中的数据正态性检验方法

本帖最后由 smart_k 于 2011-12-16 10:07 编辑

用Minitab作数据的正态性检验的方法有如下两种：
<1>.　统计>基本统计量>正态性检验 (stat>Basic Statistic>Normality test)
<2>.　统计>基本统计量>图形化汇总
最后都是看P值，P>0.05就基本可以认为数据正态（什么情况下P>0.05也不能判为正态分布？请跟帖者回答）。
一定要以最后的P-value作标准，而不能凭感觉。
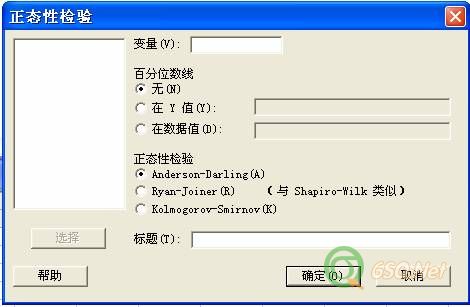
第一种方法(stat>Basic Statistic>Normality test)下有如下三种检验方法：
(1). Anderson-Daling，缺省状态即为此检验法，AD法最灵敏。AD检验是很准确的判断方法，表面上在直线附近, 但很可能被拒绝。
(2). Ryan-Joiner (它实际上与W检验很相似，ISO将它定为标准检验方法，中国国标也采用此法)。
(3). Kolmogorov-Smirnov方法。

Anderson-Darling和Kolmogorov- Smirnov检定方法是基于经验分布函数，Ryan-Joiner (类似Shapiro-Wilk)是基于相关与回归的，一般而言都选Anderson-Darling。
正态性检验的方法很多，但具体原理是不相同的。有些是拟合优度检验，有些是偏峰度检验，Minitab常用Anderson-Darling检验。
三种检验方法的详细解释如下：
Anderson-Darling检验（A-D检验），是一种基于经验累积分布函数（ECDF）的算法，特别适用于小样本（当然也适用于大样本），AD值越小，表明分布对数据拟合度越好，A-D检验只适合特定的连续分布如：normal、lognormal、exponential、Weibull、logistic、extreme-value type 1。
A-D检验是对K-S检验的一种修正，相比K-S检验它加重了对尾部数据的考量，K-S检验具有分布无关性，它的临界值并不依赖被测的特定分布，而A-D检验使用特定分布去计算临界值，这使得A-D检验具有更灵敏的优势。
Anderson-Darling 检验
选择此项将执行正态性的 Anderson-Darling 检验，此检验是将样本数据的经验累积分布函数与假设数据呈正态分布时期望的分布进行比较。如果实测差异足够大，该检验将否定总体呈正态分布的原假设。
Ryan-Joiner检验（R-J检验，类似于Shapiro-Wilk检验），是一种基于相关性的算法。R-J检验可得到一个相关系数，它越接近1就越表明数据和正态分布拟合得越好。
A-D检验和R-J检验在正态性检验中具有相似的功效，而K-S检验的功效较弱。
对于大样本的拟合度测试，通常使用卡方检验（卡方检验是一种基于概率密度函数的算法，不适合于小样本）会更好，因为卡方检测不需要分布参数的知识，并且卡方检验适用于连续和离散分布。
Ryan-Joiner 正态性检验
选择此项将执行 Ryan-Joiner 检验，此检验通过计算数据与数据的正态分值之间的相关性来评估正态性。如果相关系数接近 1，则总体就很有可能呈正态分布。Ryan-Joiner 统计量可以评估这种相关性的强度；如果它未达到适当的临界值，您将否定总体呈正态分布的原假设。此检验类似于 Shapiro-Wilk 正态性检验。
Kolmogorov-Smirnov检验（K-S检验），也是一种基于经验累积分布函数（ECDF）的算法，K-S检验最吸引人的特性是具有分布无关性，所以适用于任何连续分布，很适合小样本（当然也适合大样本）。
但是由于K-S检验相对尾部而言，往往对分布中心更敏感，并且它的临界值并不依赖被测的特定分布，相对A-D检验而言它的灵敏度较低，所以很多的分析更愿意使用A-D 拟合度检验。
Kolmogorov-Smirnov 正态性检验
选择此项将执行正态性的 Kolmogorov-Smirnov 检验，此检验是将样本数据的经验累积分布函数与假设数据呈正态分布时期望的分布进行比较。如果实测差异足够大，该检验将否定总体呈正态分布的原假设。
如果这些检验的 p 值低于你选择的 a 水平，你可以否定原假设，并断定总体呈非正态分布。
有资料上说Anderson-darling、Ryan-Joiner、Kolmogorov-Smirnov三种检验中只要有一种给出否定的结论，就应该判定该分布非正态。
实际上AD检验即使通不过，但是另外两种能通过的话，也可以当成正态分布的，因为可以把它看成近似正态分布，这个与样本的多少有关。AD检验更适合小样本数量的检验。因此，有的时候AD通不过正态，其它两种能通过，也能把数据看作近似正态分布的。
样本容量(样本中个体的数目)仅为5~10也可以进行正态性检验。但是样本容量过少时，即使是正态，也会受到置疑。因为那要看抽样时5个样本的代表性如何。
当样本数据为非正态分布或为小样本或两样本方差不等时要用非参数检验（卡方、符号、秩和等）。
用图形化汇总来验证数据是否正态携带的信息比较多，P值、峰度、偏度都会在图形化汇总中显示出来。