散点图概述

典型的散点图包含下列元素：
· 表示连续变量的值的 x 轴。按照习惯，这是预测（自）变量。

· 表示连续变量的值的 y 轴。按照习惯，这是响应（因）变量。

· 在数据的 (x, y) 坐标上图示的符号。您还可以根据需要使用不同颜色/形状的符号在相同的散点图上表示不同的组。

使用散点图评估两个变量之间的关系的方向、强度和线性：

· 同时趋向于上升的数据值指示正相关性。

· 如果随着一个数据值的降低而另一个数据值升高，则指示负的相关性。

· 关系强度越大，所生成的数据点聚类就越紧密。

· 异常值将落于远离主要点组处。

可以直观地确定关系是直线还是曲线。如果关系是曲线，则您可能需要包括高次项以准确地对弯曲程度建模（请参见多项式回归）。

当依赖时间变化的数据不是按时间顺序排列，或数据采集区间不规则时，应使用散点图而不是时间序列图。

输出示例




解释


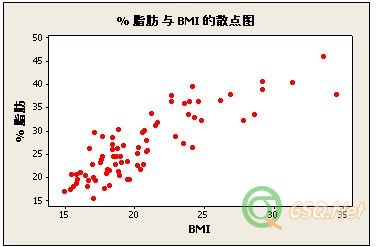
BMI 和脂肪数据的散点图显示了两个变量之间的强度很大的正线性关系。体重指数 (BMI) 可能是身体脂肪百分比的一个好的预测变量。

多项式回归
一种对响应变量 (y) 和预测变量 (x) 之间关系中的弯曲建模的方法。正确地对弯曲建模是模型描述数据和预测响应的准确程度的重要因子。要对此弯曲建模，请在回归模型中包括高次项，如 x 和 x。

例如，线性模型只能显示数据中固定的递增或递减速度，而二次模型（形状通常大致为 U 形或倒 U 形）则可以解释数据中的弯曲。立方模型可以描述数据中的“峰谷”模式。