【求教】用六西格玛知识解决一个焊接后精孔变形的问题
各位大师,小弟不是懒人,之前粗浅地接触过一些统计学的知识,但是苦于一直和民营企业打交道,这些东西都荒废了,短时间内没有时间搜索,自学,来到这里还是希望各位能帮我尽快解决一下这个实际问题,先谢谢了。
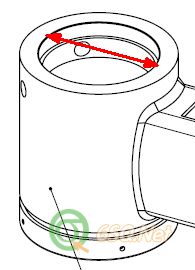
我有这样一个零件,如图这个地方是装轴承的精孔90H7(+0/+0.035),因为附近有焊疤,精孔容易变成椭圆。厂商经常超差,现我想评估其制程能力,然后决定是否需要和国外争取放大公差或是逼迫厂商重新更改工艺(焊接后再进行精加工),于是做了一下研究,不知道对不对,然后如何根据结果去和国外和厂商沟通?用Pp来说明制程能够达到的范围(>1.33可接受?)用Ppk来说明制程能力有偏斜(需要调整产品往上限做?)是否可以?
尺寸公差 90 90.035
产品数量 椭圆短边 椭圆长边
1 90.005 90.025
2 89.995 90
3 89.995 90.015
4 90 90.015
5 89.995 90.035
6 89.995 90.015
7 89.995 90.025
8 90 90.015
9 89.985 90.02
10 89.996 90.01
11 90.005 90.015
12 90.005 90.015
13 89.99 90
14 89.995 90.015
15 89.99 90.015
16 90.005 90.015
17 89.996 90.012
18 89.995 90.015
19 89.995 90.01
20 90.005 90.015
21 90.005 90.01
22 89.995 90.015
23 89.995 90.01
24 90.005 90.01
25 90.005 90.025
26 90.005 90.015
27 89.995 90.015
28 89.995 90
29 90.005 90.025
30 89.995 90.015
平均值 89.99807 90.01473
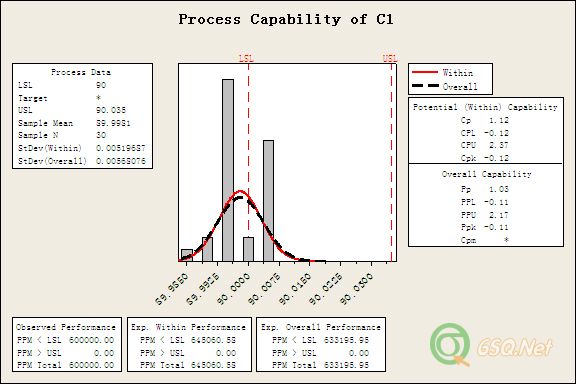
短边制程能力评估 分组数选的是1
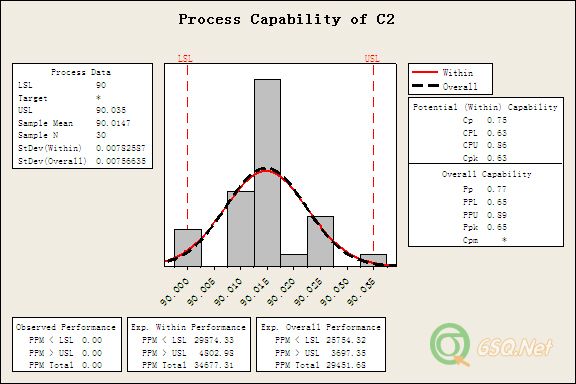
长边制程能力评估 分组数选的是1
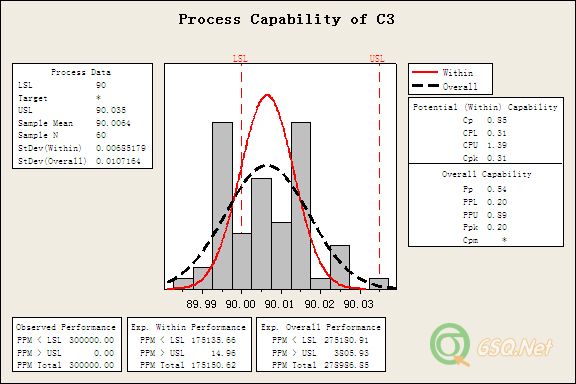
我把C1,C2长短边共60组数据又合在一起搞了一下:
我是这么算的,不知道对不对
我有这样一个零件,如图这个地方是装轴承的精孔90H7(+0/+0.035),因为附近有焊疤,精孔容易变成椭圆。厂商经常超差,现我想评估其制程能力,然后决定是否需要和国外争取放大公差或是逼迫厂商重新更改工艺(焊接后再进行精加工),于是做了一下研究,不知道对不对,然后如何根据结果去和国外和厂商沟通?用Pp来说明制程能够达到的范围(>1.33可接受?)用Ppk来说明制程能力有偏斜(需要调整产品往上限做?)是否可以?
尺寸公差 90 90.035
产品数量 椭圆短边 椭圆长边
1 90.005 90.025
2 89.995 90
3 89.995 90.015
4 90 90.015
5 89.995 90.035
6 89.995 90.015
7 89.995 90.025
8 90 90.015
9 89.985 90.02
10 89.996 90.01
11 90.005 90.015
12 90.005 90.015
13 89.99 90
14 89.995 90.015
15 89.99 90.015
16 90.005 90.015
17 89.996 90.012
18 89.995 90.015
19 89.995 90.01
20 90.005 90.015
21 90.005 90.01
22 89.995 90.015
23 89.995 90.01
24 90.005 90.01
25 90.005 90.025
26 90.005 90.015
27 89.995 90.015
28 89.995 90
29 90.005 90.025
30 89.995 90.015
平均值 89.99807 90.01473
短边制程能力评估 分组数选的是1
长边制程能力评估 分组数选的是1
我把C1,C2长短边共60组数据又合在一起搞了一下:
我是这么算的,不知道对不对
没有找到相关结果
已邀请:
本帖最后由 elysion 于 2012-8-8 11:43 编辑
我感觉。。。你是不是顺序颠倒了,正常的流程应该是控制图发现异常,然后去找问题,调整工艺。。你现在问题已经非常明确了,应该着手的是改善问题啦,你做这个能力分析有什么意义?
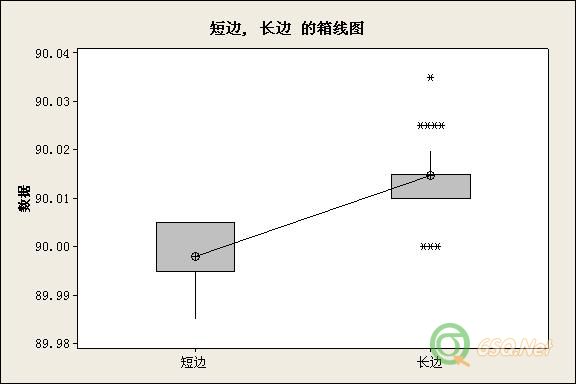
我把你的数据使用双样本T检验作了个对比结果如下:
双样本 T 检验和置信区间: 短边, 长边
短边 与 长边 的双样本 T
N 均值 标准差 均值标准误
短边 30 89.99807 0.00563 0.0010
长边 30 90.01473 0.00750 0.0014
差值 = mu (短边) - mu (长边)
差值估计值: -0.01667
差值的 95% 置信区间: (-0.02010, -0.01323)
差值 = 0 (与 ≠) 的 T 检验: T 值 = -9.73 P 值 = 0.000 自由度 = 53
你的数据部服从正态分布,仅比较数据分布情况吧。。。
我感觉。。。你是不是顺序颠倒了,正常的流程应该是控制图发现异常,然后去找问题,调整工艺。。你现在问题已经非常明确了,应该着手的是改善问题啦,你做这个能力分析有什么意义?
我把你的数据使用双样本T检验作了个对比结果如下:
双样本 T 检验和置信区间: 短边, 长边
短边 与 长边 的双样本 T
N 均值 标准差 均值标准误
短边 30 89.99807 0.00563 0.0010
长边 30 90.01473 0.00750 0.0014
差值 = mu (短边) - mu (长边)
差值估计值: -0.01667
差值的 95% 置信区间: (-0.02010, -0.01323)
差值 = 0 (与 ≠) 的 T 检验: T 值 = -9.73 P 值 = 0.000 自由度 = 53
你的数据部服从正态分布,仅比较数据分布情况吧。。。





crazyboyxu • 2014-01-14 20:23
个人觉得,抛开楼主的问题,像这种每组长短轴都可以构成一个配对的情况下,用配对t检验是否更好点呢?双样本可以判定两个样本的均值差异是否显著,但对"圆度"这个构成配对的指标(长轴-短轴)并不敏感。