MSA手册均值极差法确定GRR之均值控制图的疑问
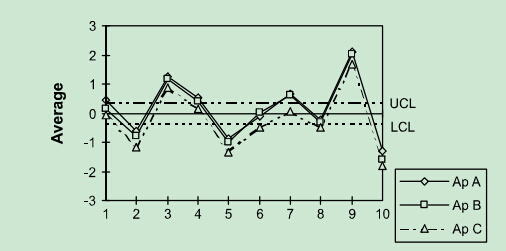
MSA手册第三章对可重复测量系统推荐的实施方法第 B 节平均值和极差法确定重复性和再现性的指南,此章节关于均值图阐述了如此一段(英文版见图1,控制图见图2):
控制图以内的区域表示测量的敏感性(干扰)。由于研究中所使用的零件代表了过程的变差,大约一半或一半以上的平均值应该落在控制限以外。如数据显示这样的图形,则测量系统应该是符合的,检验出零件之间的变差,以及能为过程的分析和控制提供有用的信息;如果少于一半的数据点落在控制限以外,则测量系统的有效分辨力不足,或这个样本不能代表过程的变差。
对此,我有以下疑问:
1、关于“控制图以内的区域表示测量的敏感性(干扰)”
如何理解此处的敏感性(干扰),使用的英文为sensitivity (“noise”)?
2、关于“如果少于一半的数据点落在控制限以外,则测量系统的有效分辨力不足,或这个样本不能代表过程的变差”
为何不能换一个角度想一想:数据点全部落在控制限以内,是由于制造过程与测量过程稳定,且能力符合。为何一定要有一半以上落在控制限以外呢?
请各位指教!
谢谢!
控制图以内的区域表示测量的敏感性(干扰)。由于研究中所使用的零件代表了过程的变差,大约一半或一半以上的平均值应该落在控制限以外。如数据显示这样的图形,则测量系统应该是符合的,检验出零件之间的变差,以及能为过程的分析和控制提供有用的信息;如果少于一半的数据点落在控制限以外,则测量系统的有效分辨力不足,或这个样本不能代表过程的变差。
对此,我有以下疑问:
1、关于“控制图以内的区域表示测量的敏感性(干扰)”
如何理解此处的敏感性(干扰),使用的英文为sensitivity (“noise”)?
2、关于“如果少于一半的数据点落在控制限以外,则测量系统的有效分辨力不足,或这个样本不能代表过程的变差”
为何不能换一个角度想一想:数据点全部落在控制限以内,是由于制造过程与测量过程稳定,且能力符合。为何一定要有一半以上落在控制限以外呢?
请各位指教!
谢谢!
没有找到相关结果
已邀请:





5 个回复
yijiayige (威望:636) (江苏 苏州) 机械制造 经理 - 工作经验超过15年,熟悉绝大多数质量相关管理和技...
赞同来自: cdl30 、mushroom159 、ff2jj47 、116066602 、csuwangweijx 、KevinSir1992 、lt0722 、TK747 、1inS 、Jackchuang 、Nick Chan更多 »
按MSA的三三制试验方法来说:
一、数理上:
控制图用控制线等于 Xbar+/- A2*Rbar(*),查常数表来说,是很小的,A2*Rbar大概只有1.5-1.6倍西格玛;
而生产用控制线,是参考正态分布的99.73%范围来拟订的,是 XBar+/-3* Rbar/d2(*),而3*Rbar/d2(*)大约是3倍西格玛;
查正态分布表估算,控制图用控制线,允许数据点在控制线内的比例约是90%左右,也就是说允许10%左右部分超出控制线范围;
而如果使用+/-3西格玛范围的时候,则允许点大约是99.73%,将会较少看到超出控制线的。
但是上面两个结论,仅适用于大样本,或被抽取的样本整体。
具体进一步的推论看下面
二、漂移许可
再加上,MSA手册中明确要求尽量取的样本总量覆盖或略超出公差带;考虑到分散性以及数据量只有10个,其原则上是不满足正态分布的;因此数理上的分析就不太适用了,则出现了点上面的漂移。
而我们知道,采样数据向两端集中的时候,类似于反正态分布图,那么就得到了一个奇怪的推论:原则上应该有不超过约90%的点处于控制线(控制图用)外比较好;
但是考虑到随机抽样且尽量偏移两端,则会形成另一个极端----“均衡态分布”,于是+/-1.5倍西格玛则刚好处于略不超过50%的覆盖范围(被抽样本总量,在抽取前覆盖原则上是满足+/-3西格玛)。
综上,就推理出一个相对比较合理的规则:
“需要有50%的点,处于控制线外”。
以上分析完毕。