请教：数据关联性强，不满足正态分布的情况下该选用Cpk or Ppk作为改善指标？还是要进行正态性数据转换？

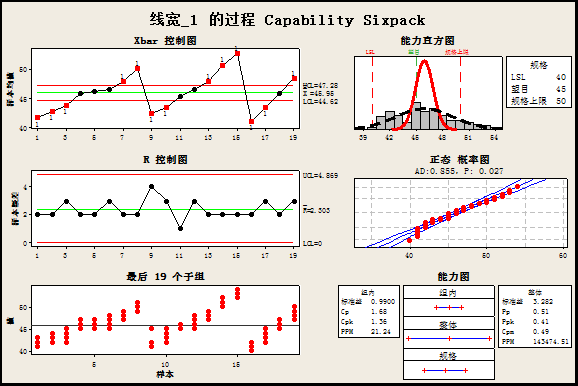
基本介绍：这是一个关于丝网印刷线宽控制的问题。印刷线宽跟网版印次显著相关，随着印次增加，线宽会逐渐变宽。考虑网版成本原因，对网版印次有一定要求。但是如此一来，保证到样本覆盖整体的情况下，抽测数据不符合正态性分布了。使用Minitab软件的capability sixpack分析，Cpk值较高，但是Ppk非常低（附图）。对这个数据，是可以直接采用Ppk作为改善指标呢？还是需要进行正态性数据转换啊？请各位高手们指点一下迷津，谢谢！

补充：已经确定过程是不稳定的，主要是印刷次数与线宽成正向相关性，随着网版印刷的次数增多线宽就越来越宽。考虑到印刷耗材成本问题，一般一块网版要印刷12000-20000片，所以线宽就会逐渐变宽。这里考虑的是根据对印刷线宽的规格要求，去对印刷次数以及其他影响线宽的因素进行控制。目前的问题是在基准调查阶段，是否可以选取Ppk作为改善指标？或者只能用其他方式作为改善指标？

可能我的问题还是没表达清楚，更加详细点的补充描述如下：
一个叫丝网印刷的工序，连续生产，每小时产能1500片，其CTQ之一是印刷线宽，其规格限是40-50。目前已经知道一块网版刚开始使用时，印刷的线宽在40左右（波动不大）。但随着网版印次的增加，线宽均值会慢慢变大，最终可能超过50。因为是连续生产，只能抽检。现在收集了一些样品，得到一些线宽数据（非正态）。目前希望通过这些数据来反映当前的过程能力，并预测到底有多少线宽会超出控制限。
一般的情况下当然是要先保证过程稳定，只有随机波动的影响，这时候大多数分布都会符合正态分布（当然也还可能有威布尔分布等）。但是，我这里的情况是已知网版印次这个因素是非随机的，而且也不可能消除。在这种情况下如何定义过程能力？并预测到底有多少线宽会超出控制限？