MINITAB方差分析，请大神指点！
1， R-Sq 和 R-Sq（调整） 这两个差异，怎么区分。
2， 分析结论从那个参数上确定，显著性水平？ 还是根据F值，怎么确定？
没有找到相关结果
已邀请:
你这个方差分析的
原假设H0：μ180=μ200=μ220；
备择假设Ha：至少有一个不等（即μ180与μ200；μ180与μ220；μ200与μ220中至少有一个不等）
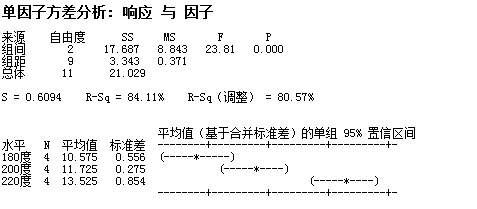
从分析中可以看出p值为0，应拒绝原假设，接受备择假设；
再结合置信区间图，可以95%确定μ180≠μ220和μ200≠μ220，表示220度与180度和200度有显著差异；
至于180度和200度之间是否存在显著性差异，由于他们的置信区间还有部分重叠，因此可再做一次单因子方差分析：
原假设H0：μ180=μ200；
备择假设Ha：μ180≠μ200；
看p值与α值之间的大小，来确定180度和200度之间是否存在显著性差异；
个人意见，仅供参考！
原假设H0：μ180=μ200=μ220；
备择假设Ha：至少有一个不等（即μ180与μ200；μ180与μ220；μ200与μ220中至少有一个不等）
从分析中可以看出p值为0，应拒绝原假设，接受备择假设；
再结合置信区间图，可以95%确定μ180≠μ220和μ200≠μ220，表示220度与180度和200度有显著差异；
至于180度和200度之间是否存在显著性差异，由于他们的置信区间还有部分重叠，因此可再做一次单因子方差分析：
原假设H0：μ180=μ200；
备择假设Ha：μ180≠μ200；
看p值与α值之间的大小，来确定180度和200度之间是否存在显著性差异；
个人意见，仅供参考！
RSS Feed
g1085136897 • 2016-05-10 19:14
写的太专业了，初学者看不懂
小书童110 • 2016-05-11 09:23
谢谢您的回复， 方差分析在结论判定上有2中方式， 1，MINITAB 的P值，2，差t表找到拒绝区域，来判定。另，R-Sq与R-Sq（调整）怎么理解？？？
milknuts • 2016-05-11 10:07
R-Sq(调整)是扣除了回归方程中所受到的包含项数的影响的相关系数，可以更准确地反映模型的好坏，要判断两个模型的优劣可以从R-Sq(调整)和R-Sq的接近程度来判断，二者之差越小则说明模型越好。
小书童110 • 2016-07-19 12:41
谢谢！！！