控制图控制线的计算和过程能力分析的相关理解和问题
前言:首先有一个确定的是,计算控制图的UCL(上控制线)和LCL(下控制线)时,公式一定为X-bar ± 3σ。但σ的计算方式有两种:当我们已知一组样本时,σ的计算方式(以单值移动极差I-MR为例)为1. σ=R-bar/d2 (这也是公认推荐的计算方法)。或者2. σ=根号(x1—x-bar)2/(n-1) [公式打字输入有点复杂,这里大家理解我的意思就行了: )]。基于以上描述,我这里想让专家们帮助确认下几个理解是否正确。
1. 理解1:以单值移动极差I-MR为例,使用σ=R-bar/d2公式计算σ的原因是:因为我不知道一个真正稳定的过程(没有异常原因/点),它的整体的标准差应该是多少。假设我知道我的过程稳定,并且有整体的所有数据,那么我就可以直接计算整体标准差σ如下:
然后得到的σ值乘以3就得到了UCL和LCL的范围。但是多数情况下,我们不可能知道总体数据,并且也不能保证我的样本是稳定的,所以我只能使用σ=R-bar/d2这个公式来计算σ,或者准确的说通过我现有的样本推算出一个稳定的总体标准差应该是多少,这个公式中的d2常数是专家们根据大量的数据计算得来的帮助矫正和优化σ数值。
2. 理解2:控制图的控制线本质就是应该尽可能的排出一切特殊原因信号的干扰,只留下真正稳定的数据计算得出控制线。
3. 理解3:基于以上理解,Cpk的σ计算方式采用σ=R-bar/d2此公式,代表在计算Cpk时有意识的排除了异常点导致σ偏大的情况,所以我们称Cpk为潜在能力指数,代表一个流程的最佳状态时,它的过程能力。而Ppk的σ计算方式采用 根号(x1—x-bar)2/(n-1),因此Ppk的结果更容易被当前真实的数据所干扰,反映的是当前实际过程性能。
1. 理解1:以单值移动极差I-MR为例,使用σ=R-bar/d2公式计算σ的原因是:因为我不知道一个真正稳定的过程(没有异常原因/点),它的整体的标准差应该是多少。假设我知道我的过程稳定,并且有整体的所有数据,那么我就可以直接计算整体标准差σ如下:
然后得到的σ值乘以3就得到了UCL和LCL的范围。但是多数情况下,我们不可能知道总体数据,并且也不能保证我的样本是稳定的,所以我只能使用σ=R-bar/d2这个公式来计算σ,或者准确的说通过我现有的样本推算出一个稳定的总体标准差应该是多少,这个公式中的d2常数是专家们根据大量的数据计算得来的帮助矫正和优化σ数值。
2. 理解2:控制图的控制线本质就是应该尽可能的排出一切特殊原因信号的干扰,只留下真正稳定的数据计算得出控制线。
3. 理解3:基于以上理解,Cpk的σ计算方式采用σ=R-bar/d2此公式,代表在计算Cpk时有意识的排除了异常点导致σ偏大的情况,所以我们称Cpk为潜在能力指数,代表一个流程的最佳状态时,它的过程能力。而Ppk的σ计算方式采用 根号(x1—x-bar)2/(n-1),因此Ppk的结果更容易被当前真实的数据所干扰,反映的是当前实际过程性能。
没有找到相关结果
已邀请:
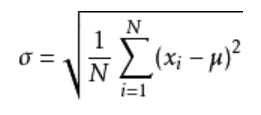





5 个回复
杨格_Alan (威望:668) (江苏 无锡) 机械制造
赞同来自: Young120
您的根本问题在于:将基于样本计算的统计量认作是总体的参数真值了。这是不对的,应该是估计。
您所有写的公式上都少了一个^: 点估计的意思。