一道DOE问题求教:田口分析和ANOVA的关系
本人最近在做一个QCC,其中做了一个3因子3水准的田口实验设计。
实验目的是通过调节paste depth,soaking time及speed 3因子的不同水准,得到
产品某个部位尺寸的最佳Cpk。田口实验表及实验数据如下:(其中不同实验条件下的CPK是多次实验结果的均值)
paste depth soaking time speed Cpk SNRA1
1 1 1 1.30000 2.2789
1 2 2 1.05600 0.4733
1 3 3 1.52000 3.6369
2 1 2 2.07000 6.3194
2 2 3 1.81000 5.1536
2 3 1 1.45500 3.2573
3 1 3 1.02400 0.206
3 2 1 0.08700 -21.2096
3 3 2 0.39000 -8.1787
SNRA1是由minitab望大生成
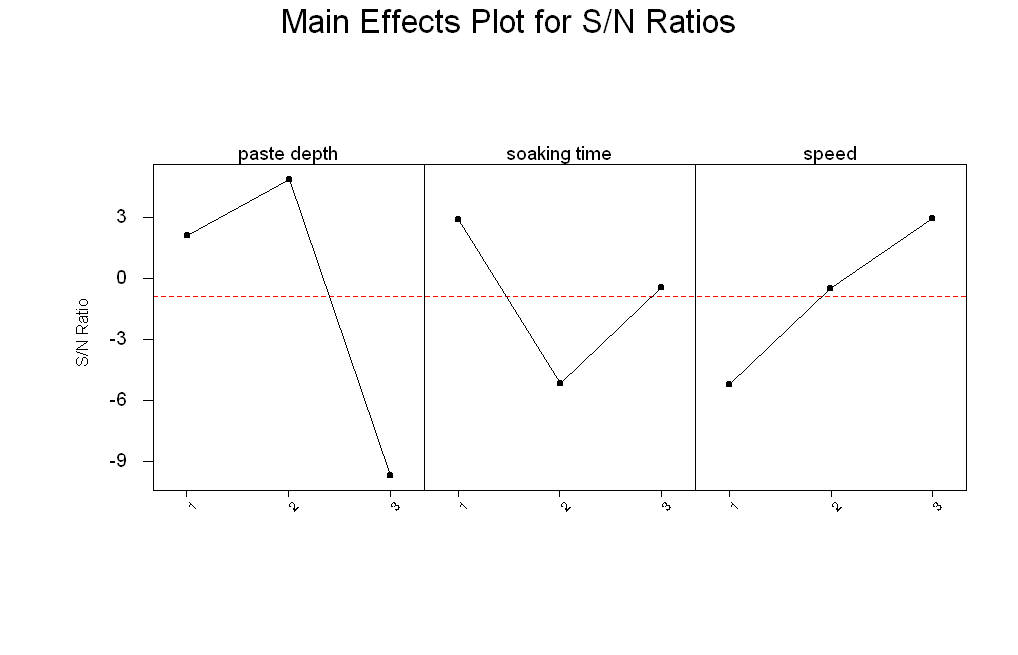
田口分析如下
Main Effects for Means: Cpk
Response Table for Signal to Noise Ratios
Larger is better
Level paste depth soaking time speed
1 2.1297 2.93476 -5.22450
2 4.9101 -5.19426 -0.46201
3 -9.7274 -0.42819 2.99881
Delta 14.6375 8.12901 8.22331
Rank 1 3 2
Response Table for Means
Level paste depth soaking time speed
1 1.29200 1.46467 0.94733
2 1.77833 0.98433 1.17200
3 0.50033 1.12167 1.45133
Delta 1.27800 0.48033 0.50400
Rank 1 3 2
实验目的是通过调节paste depth,soaking time及speed 3因子的不同水准,得到
产品某个部位尺寸的最佳Cpk。田口实验表及实验数据如下:(其中不同实验条件下的CPK是多次实验结果的均值)
paste depth soaking time speed Cpk SNRA1
1 1 1 1.30000 2.2789
1 2 2 1.05600 0.4733
1 3 3 1.52000 3.6369
2 1 2 2.07000 6.3194
2 2 3 1.81000 5.1536
2 3 1 1.45500 3.2573
3 1 3 1.02400 0.206
3 2 1 0.08700 -21.2096
3 3 2 0.39000 -8.1787
SNRA1是由minitab望大生成
田口分析如下
Main Effects for Means: Cpk
Response Table for Signal to Noise Ratios
Larger is better
Level paste depth soaking time speed
1 2.1297 2.93476 -5.22450
2 4.9101 -5.19426 -0.46201
3 -9.7274 -0.42819 2.99881
Delta 14.6375 8.12901 8.22331
Rank 1 3 2
Response Table for Means
Level paste depth soaking time speed
1 1.29200 1.46467 0.94733
2 1.77833 0.98433 1.17200
3 0.50033 1.12167 1.45133
Delta 1.27800 0.48033 0.50400
Rank 1 3 2
没有找到相关结果
已邀请:





8 个回复
蚂蚁 (威望:8) (广东 深圳) 咨询业 咨询顾问
赞同来自:
2.如果田口方法没有设计噪声因子,将仅对误差因子的影响极差进行计算,并作简单排序,其输出结果还没有方差分析结果详细。
看看下面的分析结果:
Taguchi Analysis: cpk versus A, B, C
Response Table for Signal to Noise Ratios
Nominal is best (10*Log(Ybar2/s2))
Level A B C
1 *
2 *
3 *
Delta *
Rank 2 2 2
Response Table for Means
Level A B C
1 1.2920 1.4647 0.9473
2 1.7783 0.9843 1.1720
3 0.5003 1.1217 1.4513
Delta 1.2780 0.4803 0.5040
Rank 1 3 2
Main Effects Plot (data means) for Means
ERROR No graphs will be plotted for SN ratios. All values are missing.
3.3因子3水平采取L9正交表,仅能评估主效应,交互作用与主效应混淆,如果要评估交互作用,需采用L27设计。可以看看L9正交表,其中3列为主效应,误差为剩余的一列。
A B C D
1 1 1 1
1 2 2 2
1 3 3 3
2 1 2 3
2 2 3 1
2 3 1 2
3 1 3 2
3 2 1 3
3 3 2 1
4.从交互作用图来看,交互作用非常明显,需要进一步估计量化,而采用L9正交表设计来做回归分析肯定就有问题,因为此时的回归分析由于解析度太低,或者说没有合理设计交互作用而是回归失败,这从方差分析P值、系数检验P值、以及R-Sq值都可以看出。
:D