测量系统分析案例-测量系统的能力指数
无论在六西格玛还是在体系的质量工具的培训中,绝大部分涉及测量系统分析的内容都可称为类型2的量具研究。我在上一篇(数据收集篇之十二)中指出,测量系统分析是一种试验设计,涉及内容众多,试验过程较复杂且用时较长,因此在测量系统分析初期可以考虑先实施类型1的测量系统分析。
通常欧洲企业会要求先做类型1,如果不达标可以立即着手改进,待达标后再考虑做类型2。而美国企业较多直接做类型2,在AIAG的手册中也未提及类型1,这可能就是六西格玛教材很少涉及类型1的原因吧。
类型1的分析原理借鉴了过程能力分析,所以也被称为测量系统(量具)过程能力分析,类似于Cp、Cpk,测量系统能力指数为Cg、Cgk。
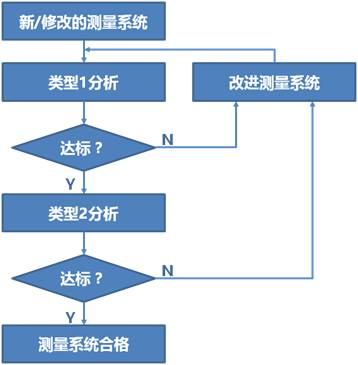
一般测量系统分析的流程可以下图描述。
测量系统能力指数
类型1主要研究的是测量系统的偏倚和重复性,并以能力指数来评价测量系统的能力。具体做法是选择一个标准件或用高等级量仪测得的参考工件,用被研究的量具进行多次测量,通常的要求是为50次,至少要有25次以上。如果测量过程中需要有人操作,要指定一个人来完成所有的测量。
在这样的试验条件下,不存在再现性,也没有过程变异,测量结果表现出的变异属于重复性变异。通常好的测量系统带来的变异应远远小于过程变异或容差T,如果要用容差来计算测量系统的能力指数,其结果要远远大于过程能力指数计算出的结果。为了使测量系统能力指数与过程能力指数在量上相当,需要缩小容差纳入计算的范围,通常将其范围缩小到容差的20%,有的公司取0.15或其它值。由此我们得到Cg的计算公式:
其中Sg为测量结果计算出的标准差,因为样本量较大,因此无需用极差R来估计,也无需采用C4来校正。
设被测标准件/工件的参考值为xm,测量结果的均值为
,则Cgk为:
式中绝对值部分为偏倚,其显著性通过t检验来确认。
与过程能力指数类似,Cg和Cgk大于1.33,测量系统可接受,否则需要对测量系统进行改进。熟悉过程能力指数的人应该很容易理解Cg和Cgk之间的关系,我这里就不再展开了。
将公式变换一下,可以估计测量系统的%P/T为:
在Cg为1.33时,可以大致估计%P/T为15%。若要达到10%以下,则Cg需要大于2。当然这只是一个大致的估计,因为这里不包含再现性,也不是覆盖整个过程变异的重复性。如果实际的测量过程不包含显著的再现性,如很少人工干预的在线量仪,这个值不失为一个有效的估计。
上式未包含偏倚,加上偏倚,则:
这个值一般要求大于15%,也就是Cgk要大于1.33。
当过程指标没有规格限或只有单边规格限时,可以用已知的历史过程变异σp来计算:
同样可以推导出%P/Tv为:
Cg、Cp与%P/Tv
对于一般的过程特性,我们一般要求Cpk要大于1.33,对应的Cp要比这个值大一些。对于精度要求很高的过程特性,Cpk要大于1.5甚至1.67。在测量系统中,我们通常要求%P/T和%P/Tv最好为10%以下,但有时20%也是可以接受的,此时Cg应为多少呢?
根据%P/Tv的定义可知
两边同时除T,我们可以得到这样的关系:
变换一下,可以得到这样的公式:
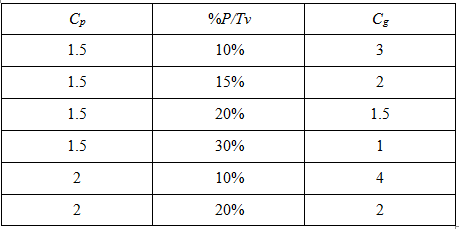
下表列出了一些典型计算结果:
以上的分析假设测量系统的变异只包含了重复性,且与GR&R中的重复性相差较小。如果测量过程中还包含显著的再现性,则对Cg的要求还要提高。
通过以上的分析,我们可以大致搞清楚Cg、Cgk的适用范围,即较少人为干预的测量系统,其中不存在显著的再现性变异。Cg、Cgk在实际的应用中很有意义。当前生产线自动化程度越来越高,很多原来需要人工检验的特性参数现在完全可以实现全自动检验,此时用Cg、Cgk来进行日常的测量系统评价就比较恰当。另外,该指数试验过程简单、便捷,利于快速了解测量系统的能力,在建立新的过程特性参数时可以加快部署的速度。
以上是我对测量系统能力指数的一点粗浅认识,欢迎对此有深入研究者提出批评意见。
分析案例
假设某特性参数的规格为5.0±0.1,选择参考值为5.0的一个标准件,在所有测量条件保持不变的条件下重复测量50次,得到50个测量值。
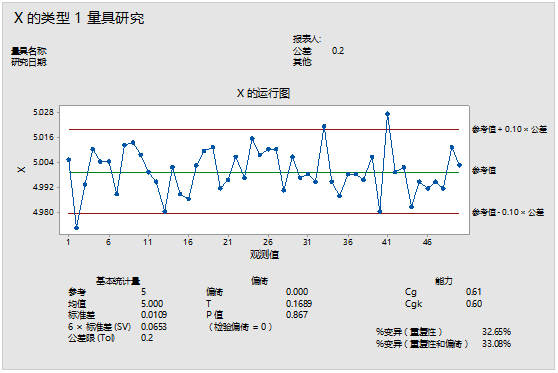
运用minitab分析得到如下结果。
图中t检验显示不存在偏倚。Cg=0.61、Cgk=0.6,均小于1.33,而两个%变异也都小于15%,说明该测量系统不达标,需要立即着手改进。
测量值的运行图以参考值±0.1倍公差作为上下限,图上有一些测量值超出了上下限,直观结论为重复性变异较大。
下图展示出一个较好的结果。
建议:
在设计实施类型2的测量系统分析之前不妨先做一下类型1,这样可以提高类型2的成功率,从而减少类型2的试验次数,既省时又省力。
在生产过程中要关注Cg、Cp与%P/Tv的关系,如果对过程的要求发生变化,对Cg要求也要跟着改变。
通常欧洲企业会要求先做类型1,如果不达标可以立即着手改进,待达标后再考虑做类型2。而美国企业较多直接做类型2,在AIAG的手册中也未提及类型1,这可能就是六西格玛教材很少涉及类型1的原因吧。
类型1的分析原理借鉴了过程能力分析,所以也被称为测量系统(量具)过程能力分析,类似于Cp、Cpk,测量系统能力指数为Cg、Cgk。
一般测量系统分析的流程可以下图描述。
测量系统能力指数
类型1主要研究的是测量系统的偏倚和重复性,并以能力指数来评价测量系统的能力。具体做法是选择一个标准件或用高等级量仪测得的参考工件,用被研究的量具进行多次测量,通常的要求是为50次,至少要有25次以上。如果测量过程中需要有人操作,要指定一个人来完成所有的测量。
在这样的试验条件下,不存在再现性,也没有过程变异,测量结果表现出的变异属于重复性变异。通常好的测量系统带来的变异应远远小于过程变异或容差T,如果要用容差来计算测量系统的能力指数,其结果要远远大于过程能力指数计算出的结果。为了使测量系统能力指数与过程能力指数在量上相当,需要缩小容差纳入计算的范围,通常将其范围缩小到容差的20%,有的公司取0.15或其它值。由此我们得到Cg的计算公式:
其中Sg为测量结果计算出的标准差,因为样本量较大,因此无需用极差R来估计,也无需采用C4来校正。
设被测标准件/工件的参考值为xm,测量结果的均值为
,则Cgk为:
式中绝对值部分为偏倚,其显著性通过t检验来确认。
与过程能力指数类似,Cg和Cgk大于1.33,测量系统可接受,否则需要对测量系统进行改进。熟悉过程能力指数的人应该很容易理解Cg和Cgk之间的关系,我这里就不再展开了。
将公式变换一下,可以估计测量系统的%P/T为:
在Cg为1.33时,可以大致估计%P/T为15%。若要达到10%以下,则Cg需要大于2。当然这只是一个大致的估计,因为这里不包含再现性,也不是覆盖整个过程变异的重复性。如果实际的测量过程不包含显著的再现性,如很少人工干预的在线量仪,这个值不失为一个有效的估计。
上式未包含偏倚,加上偏倚,则:
这个值一般要求大于15%,也就是Cgk要大于1.33。
当过程指标没有规格限或只有单边规格限时,可以用已知的历史过程变异σp来计算:
同样可以推导出%P/Tv为:
Cg、Cp与%P/Tv
对于一般的过程特性,我们一般要求Cpk要大于1.33,对应的Cp要比这个值大一些。对于精度要求很高的过程特性,Cpk要大于1.5甚至1.67。在测量系统中,我们通常要求%P/T和%P/Tv最好为10%以下,但有时20%也是可以接受的,此时Cg应为多少呢?
根据%P/Tv的定义可知
两边同时除T,我们可以得到这样的关系:
变换一下,可以得到这样的公式:
下表列出了一些典型计算结果:
以上的分析假设测量系统的变异只包含了重复性,且与GR&R中的重复性相差较小。如果测量过程中还包含显著的再现性,则对Cg的要求还要提高。
通过以上的分析,我们可以大致搞清楚Cg、Cgk的适用范围,即较少人为干预的测量系统,其中不存在显著的再现性变异。Cg、Cgk在实际的应用中很有意义。当前生产线自动化程度越来越高,很多原来需要人工检验的特性参数现在完全可以实现全自动检验,此时用Cg、Cgk来进行日常的测量系统评价就比较恰当。另外,该指数试验过程简单、便捷,利于快速了解测量系统的能力,在建立新的过程特性参数时可以加快部署的速度。
以上是我对测量系统能力指数的一点粗浅认识,欢迎对此有深入研究者提出批评意见。
分析案例
假设某特性参数的规格为5.0±0.1,选择参考值为5.0的一个标准件,在所有测量条件保持不变的条件下重复测量50次,得到50个测量值。
运用minitab分析得到如下结果。
图中t检验显示不存在偏倚。Cg=0.61、Cgk=0.6,均小于1.33,而两个%变异也都小于15%,说明该测量系统不达标,需要立即着手改进。
测量值的运行图以参考值±0.1倍公差作为上下限,图上有一些测量值超出了上下限,直观结论为重复性变异较大。
下图展示出一个较好的结果。
建议:
在设计实施类型2的测量系统分析之前不妨先做一下类型1,这样可以提高类型2的成功率,从而减少类型2的试验次数,既省时又省力。
在生产过程中要关注Cg、Cp与%P/Tv的关系,如果对过程的要求发生变化,对Cg要求也要跟着改变。
没有找到相关结果
已邀请:
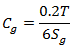
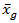
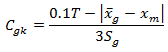

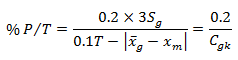
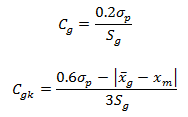
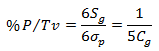
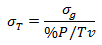
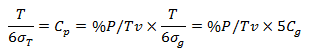







1 个回复
孤帆远影520 (威望:53) (江苏 扬州) 汽车制造相关 主管
赞同来自: 安好_963