过程能力分析02—Box-Cox变换

在上一文章《过程能力分析01—不要忽略“稳定”》中，我们强调了做过程能力分析之前需要稳定的过程，在本篇文章中我们来讨论另外一个前提-数据正态。其中我们在之前的文章中对正态性问题已经有过一些讨论，详见《数据非正态如何分析？您可能问了错误的问题！》 但是今天我们想进一步讨论非正态数据能力分析的处理办法。

非正态解决方案

如果您使用为正态数据设计的能力分析，您的数据必须服从正态分布。如果您的数据不是正态的，则分析结果可能不准确，但是我们可以通过以下方法来获得准确描述生成非正态数据的过程的能力指数。



正如你说看到的，解决方法有很多，当然方法选择不同结果肯定是有差异的，那么问题又来了，哪个方法是比较合适的呢？别急，我们可以先参考以下路径图帮助我们选择。



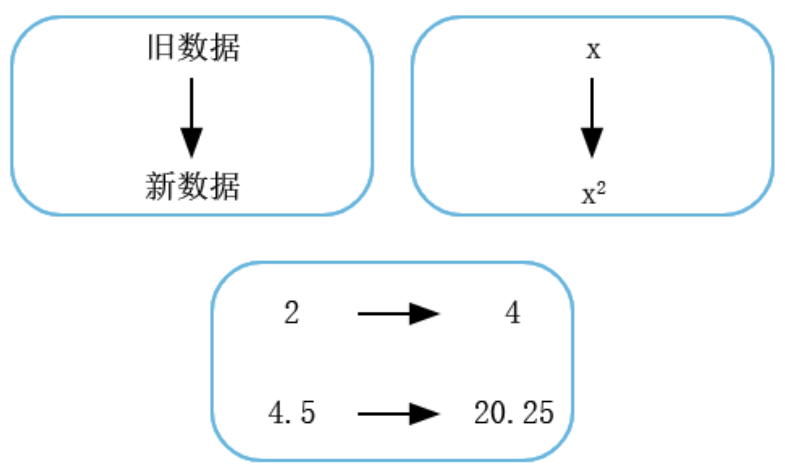
在这篇文章中，我们先来看看数据变换的方法-Box-Cox变换。为了说明数据变换方法，可以想象一下密码员将文本变换为编码消息的方法。当密码员对消息加密时，他们不更改其含义，只更改其外观。



同样，我们可以变换数据值，使数据外观发生变化。数学变换提取数据集中的现有数字，将它们插入到函数中。变换不更改数据的物理含义，仅更改它们的值。如果能够找到使非正态数据看上去像正态数据的变换，则可以使用早先了解的正态能力工具来计算过程数据的能力指数。



案例背景

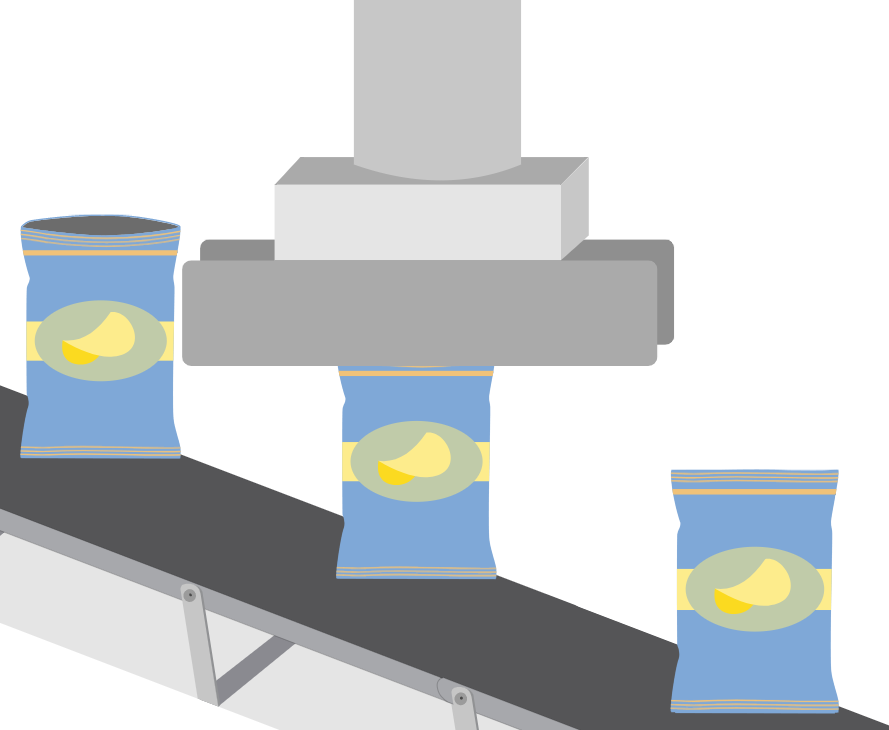
密封马铃薯片袋子。操作员将每个袋子插入到两个金属柱之间，其中一个金属柱已加热，用于将袋口密封。如果封口强度太弱，袋子在货运过程中可能会打开。如果封口强度太强，顾客可能很难打开袋子。封口强度是打开袋子所需的力量。为了研究过程，操作员从一个批次中随机采样了 250 个袋子，测量它们的封口强度。





对此列数据，我们先来一个图形化汇总（统计-基本统计-图形化汇总）。



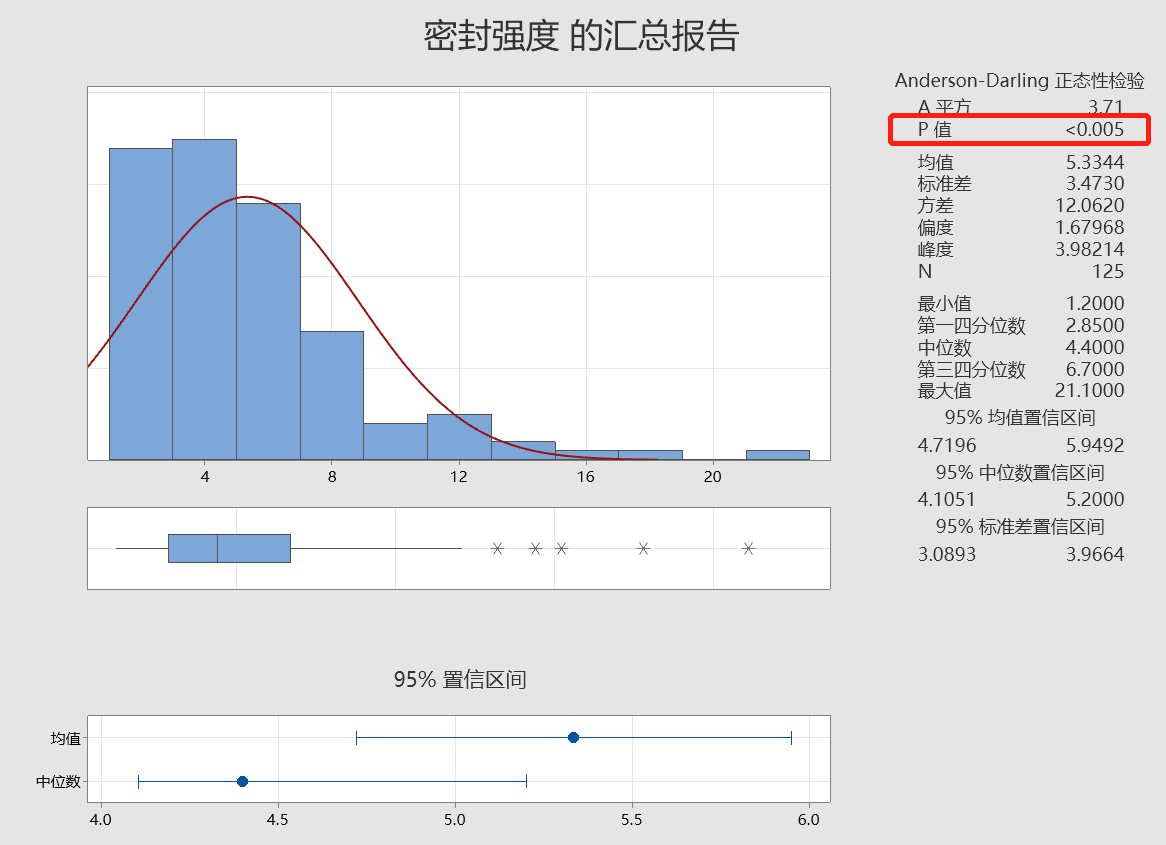
直方图右侧偏斜，Anderson-Darling 检验的 p 值小于 0.05，数据非正态，我们尝试变换数据。
在尝试变换之前，建议先执行“个体分布标识”，因为并不是所有数据都可以变换成功。





在个体分布标识中包含：正态分布+2种变换+13种其他分布，一共16种选择。



从“拟合优度检验”的结果中可以看到，两种变换都是可以的（P值大于0.05）。

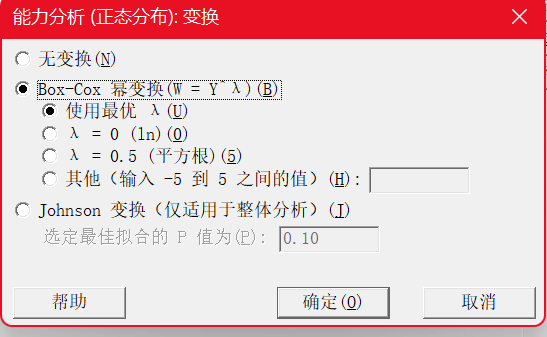
Box-Cox变换

Box-Cox 变换是一种幂变换，其中，y是初始数据值，λ 是变换参数（-5≤λ≤5），?∗是变换后的数据。 



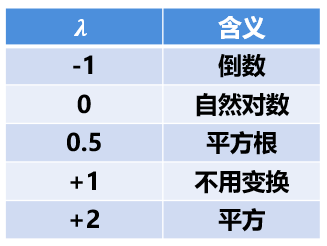
变换的关键在于找到合适的变换参数λ，下面是一些常见的λ取值和对应的变换方式。



变换的目标是找到将非正态数据变换为正态分布数据的λ。最佳变换将生成变异性尽可能小的数据集。我们可以借助Minitab来找到合适的λ。









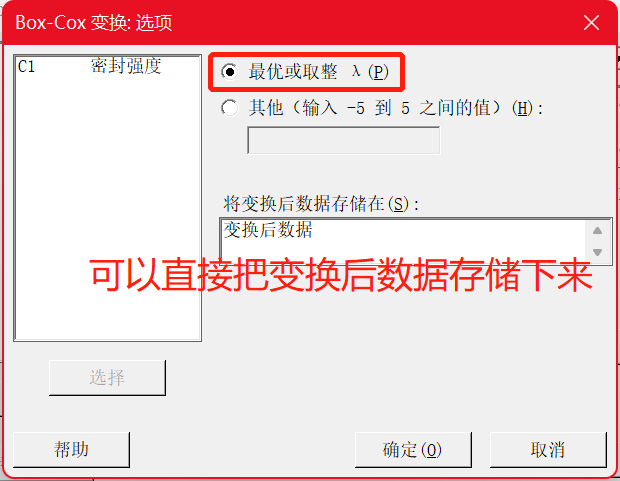
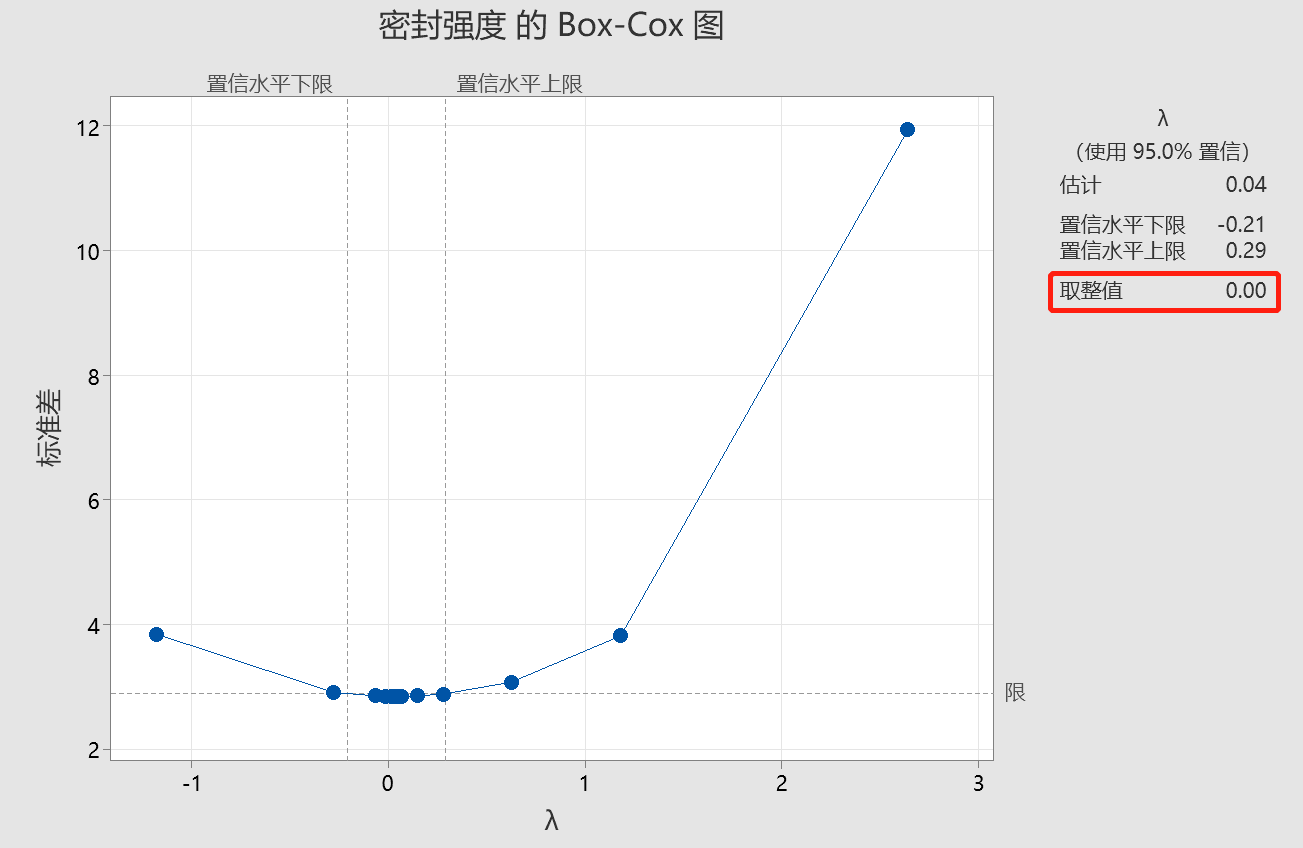
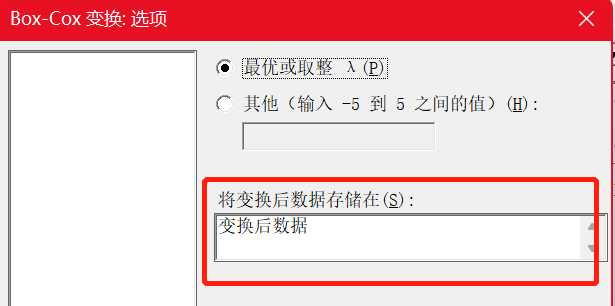
从输出的Box-Cox图中，可以发现λ的估计值0.04可以最大程度地减小Y函数标准差。但在任何实际情况下，你可能需要一个对应于容易理解的变换的λ值，如平方根（λ 为 0.5）或自然对数（λ为0）。在此示例中，λ=0是一个合理的选择，因为它处于 95% 置信区间内。因此，自然对数变换可能优先于 λ 的最佳估计值定义的变换。另外，如果选择了“将变换后数据存储在”，Minitab将会基于取整值自动帮助我们完成变换，并把数据存储下来。





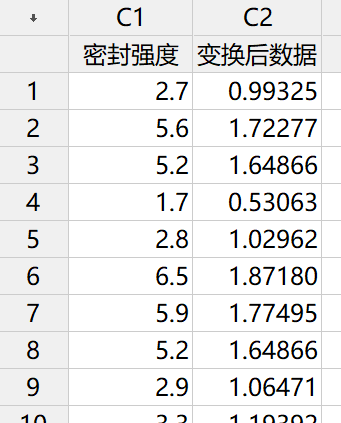
C2列是通过对C1列取自然对数得到的（λ=0）。
我们再来对变换后数据来一次正态性检验（其实没必要，这里只是为了说明转换成功与否）。



从上面结果中发现，数据已经变得正态了，Box-Cox变换成功，后面就是按照正态方法执行过程能力分析了，不再赘述。

写在最后

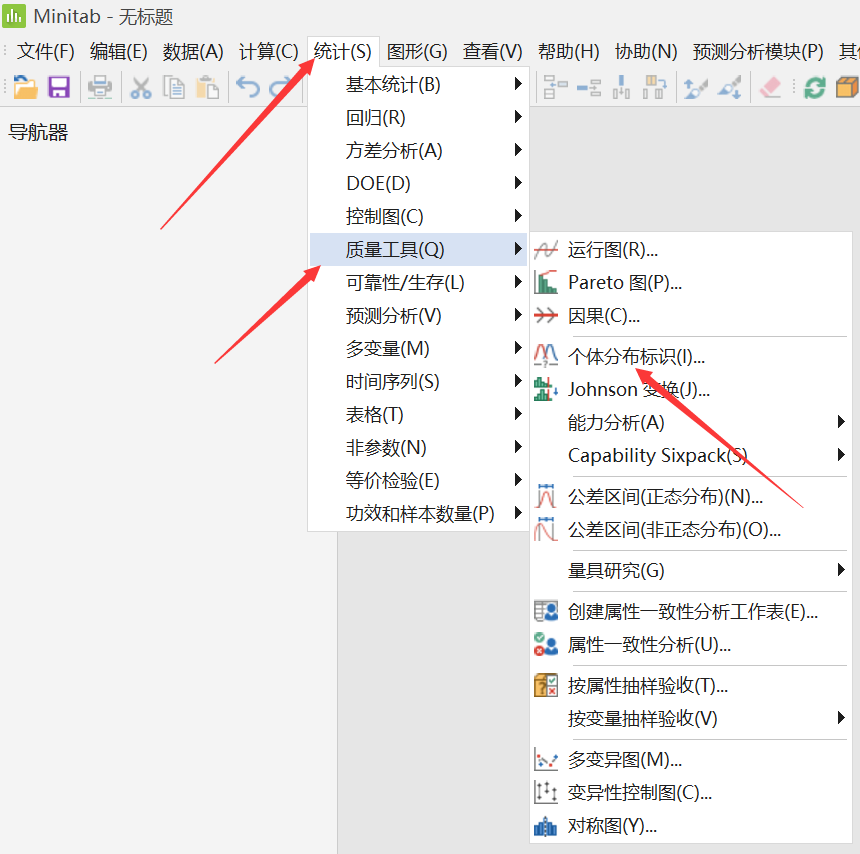
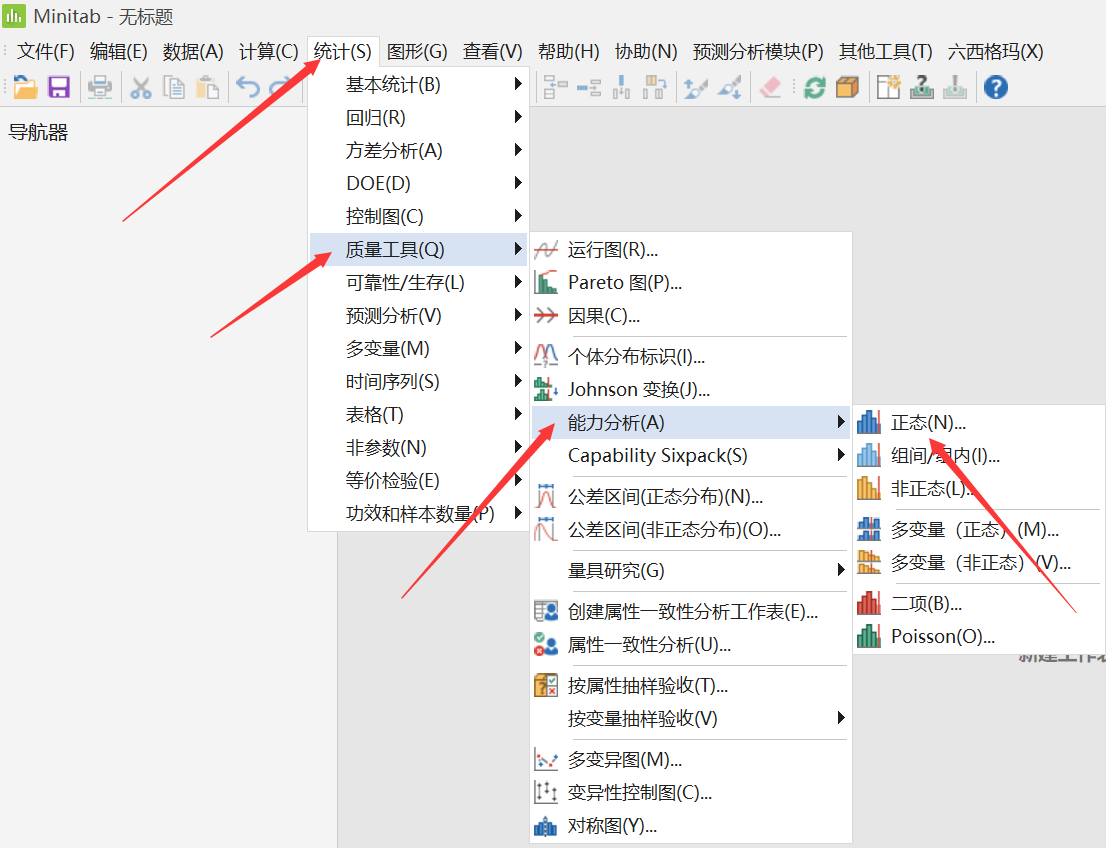
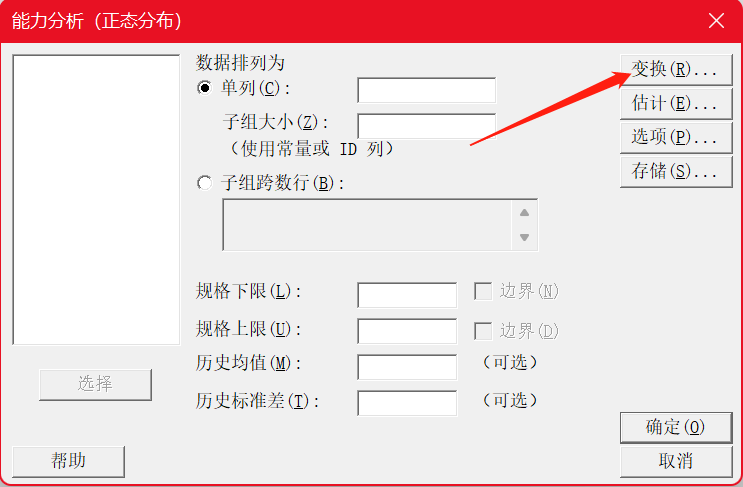
上面对Box-Cox变换做了一些介绍，其实它有很多应用方面，比如在DOE中也会用到。另外，如果是做过程能力分析，其实做Box-Cox变换有更简单的操作：在“个体分布标识”结果中，如果确定变换可行，则可以直接通过以下路径完成能力分析。